离线瞬态社会网络中的多用户位置邻近预测
廖国琼王汀利邓 琨万常选
1(江西财经大学信息管理学院 南昌 330013)2(江西省高校数据与知识工程重点实验室(江西财经大学) 南昌 330013) (liaoguoqiong@163.com)
离线瞬态社会网络中的多用户位置邻近预测
廖国琼1,2王汀利1邓 琨1,2万常选1,2
1(江西财经大学信息管理学院 南昌 330013)2(江西省高校数据与知识工程重点实验室(江西财经大学) 南昌 330013) (liaoguoqiong@163.com)
离线瞬态社会网络(offline ephemeral social network, OffESN)是一种在特定时间通过参加特定事件临时组建的新型社会网络.随着移动智能终端的普及和短距离通信技术(如蓝牙、RFID技术等)的发展,该类型网络得到工业界和学术界越来越多的关注.位置邻近(location proximity)关系是指用户在离线网络中的相遇关系.针对位置邻近关系的动态变化性及持续时间短等特征,主要研究离线瞬态社会网络中多用户邻近关系预测问题.首先,给出离线瞬态社会网络中的相关概念及问题定义;然后,设计多用户邻近关系预测总体框架,包括网络片段收集、叠加网络构建、网络过滤及极大紧密子图发现等步骤.由于多邻近关系的数量及每个邻近关系中用户的数量不能事先确定,基于分裂思想提出了一种极大紧密子图挖掘策略,以预测多用户位置邻近关系.该挖掘算法是以加权边介数为网络分裂依据,以聚集密度为分裂结束条件.在2个真实数据集上完成了实验,验证了所提出预测策略的可行性及效率.
社会网络;瞬态社会网络;位置邻近;极大紧密子图;链接预测
近年来,随着Internet技术的快速发展,在线社会网络(online social networks),如Facebook,Linkin,Twitter,QQ等已成为人们即时通信、分享消息及交友的方便快捷平台[1].与此同时,随着移动智能终端的普及和短距离通信技术(如蓝牙、RFID等)的快速发展,离线瞬态社会网络(offline ephe-meral social network, OffESN)开始得到越来越多的关注[2-6].
OffESN是人们在特定时间通过参加特定事件(如参加学术会议、博览会等[4])临时组建的社会网络.不同于在线社会网络中相对稳定的朋友关系(friendship),OffESN中的社会关系主要是通过蓝牙、RFID等短距离通信技术收集到的位置邻近(location proximity)关系[3],即用户相遇关系.不同于基于位置社会网络(location-based social network, LBSN),OffESN更多关注的是用户是否相遇,而不关心用户在何处相遇.OffESN中的位置邻近关系主要具有4个特征:
1) 面对面接触(face-to-face contact).不同于在线社会网络,OffESN中的位置邻近关系是通过离线的面对面接触形成.
2) 事件驱动(event-driven).OffESN主要包含2类事件:预定事件(prescheduled events)和自发事件(spontaneous events)[6].位置邻近关系是伴随着这些事件的开始而产生、事件的结束而消失.
3) 动态性.OffESN中的位置邻近关系是动态变化的,即用户的相遇关系随时间的变化而变化.
4) 持续时间短.OffESN中事件的持续时间通常较短.例如,在由参加学术会议形成的OffESN中,预定事件(如主题报告或分组讨论)的持续时间一般为0.5~1 h, 而自发事件的持续时间通常在0.5 h之内.
在离线瞬态社会网络中,一群人常常聚集在一起参加活动或交流.例如在参加学术会议时,几个人可能结伴一起去听学术报告,也可能聚集在一起讨论感兴趣的话题.因此,分析OffESN中多个用户之间的邻近关系,对进一步揭示该类型网络的特征具有重要意义.同时,由于短距离通信技术的局限,如信号不稳定、信号遮挡及电量不足等原因,可能会导致一些位置邻近关系未被探测到,预测多用户邻近关系可用于帮助发现缺失的位置邻近关系.
链接预测(link prediction)是社会网络分析的重要研究方向之一,最早由Liben-Nowell和Kleinberg提出[7],其任务是利用网络中的已知信息预测未来可能发生的链接.链接预测在实际应用中具有重要意义,如推荐商品、发现缺失链接、识别错误链接等,得到了研究者的广泛关注.目前在线社会网络链接预测取得了较多研究成果,主要有基于相似性度量[7-9]、基于分类模型[10-11]、基于概率关系模型[12-14],基于时间序列模型[15-16]等方法.
针对OffESN的链接预测研究已开始得到学者们的关注.文献[4]基于学术会议数据集的分析结果及社会关系理论对OffESN的特征进行了分析,并利用因子图模型预测用户两两之间的地理巧遇.文献[5]通过分析OffESN链接预测的影响因素,基于位置邻近概念提出了新邻近关系和重复邻近关系预测策略.然而,这些方法只能预测OffESN中用户两两之间的位置邻近关系.由于OffESN缺乏用户偏好以及用户对事件的评论信息,文献[6]提出了一种潜在网络融合模型(latent network fusion)进行用户潜在偏好分析,通过预测用户兴趣进行事件推荐.该模型只能预测用户与事件之间的链接.
与上述预测两两之间是否可能产生链接不同,多用户邻近关系预测是预测多个用户在未来是否可能相遇,已有链接预测策略不能直接应用于多用户邻近关系预测.就笔者所知,目前尚无文献对OffESN中的多用户邻近关系进行预测,其主要挑战包括:
1) 如何衡量OffESN中多个用户的紧密程度;
2) 在给定时刻,发生的多用户邻近关系数量及参与每个邻近关系的用户数量事先不确定;
3) 多用户邻近关系持续时间较短,且随时间的变化而发生变化.
1 问题定义

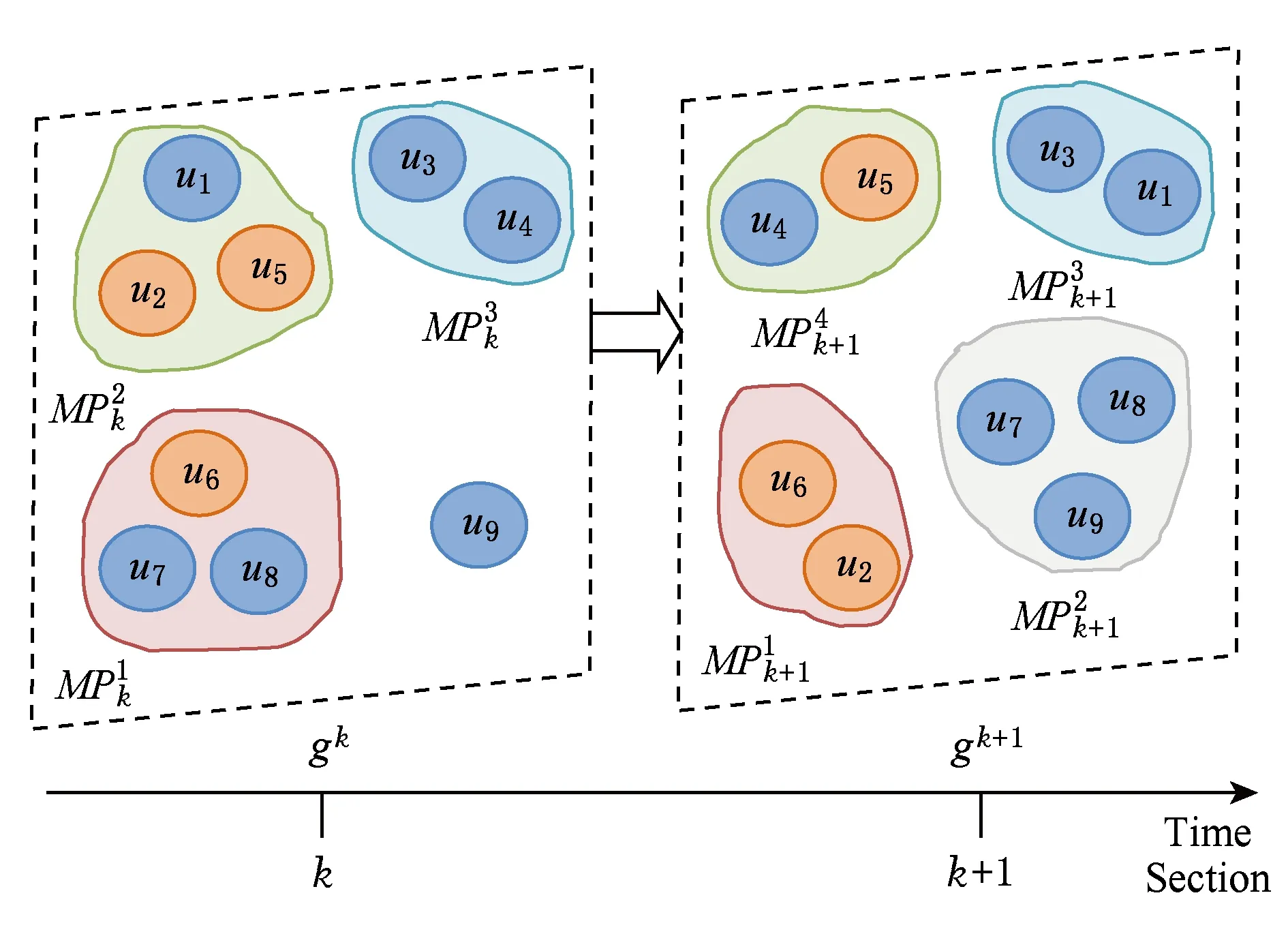
Fig. 1 An example of multi-user location proximity.图1 多用户位置邻近关系示例
定义1. 多用户位置邻近.在任意时间段,如果探测到N(N≥2)个用户两两相遇(相互邻近时间超过指定时间阈值),则称这N个用户在该时间段发生多用户位置邻近.
我们将OffESN按时间段建模成不同的网络片段(network fragment).

假设(时间依赖性): 若2个用户在时刻t相遇,则他们在时刻t+1很可能再次相遇.
ACM SIGCOMM国际学术会议于2009-08-17—2009-08-21在西班牙巴塞罗那召开.会议组织方通过蓝牙设备收集了76位参会代表会议召开期间的位置邻近数据[17].我们探测到的所有两两位置邻近关系按天划分为0~4共5个时间段.
图2为第1~4个时间段中的邻近关系对前一个时间段的时间依赖性.其中,Independent表示在上一个时间段未发生位置邻近的用户在下一个时间段发生位置邻近的比例,Dependent表示上一个时间段发生位置邻近的用户在下一个时间段仍然邻近的比例.
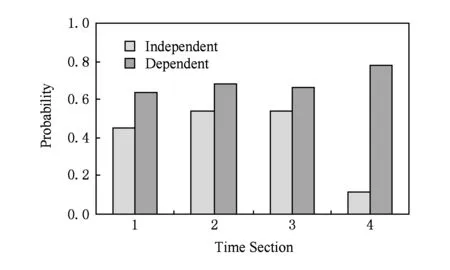
Fig. 2 Time dependency of location proximity.图2 位置邻近关系的时间依赖性
从图2可以看出,在不同的时间段,Dependent值都高于Independent,验证了如果用户在上一个时间段发生位置邻近则他们在当前时间段发生位置邻近的可能性较高,即位置邻近行为具有时间依赖性.于是,利用用户的历史邻近信息,将多个连续网络片段进行叠加,形成1个保存历史邻近关系的完整网络.

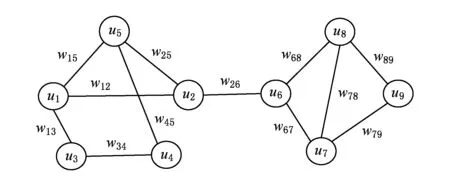
Fig. 3 An example of overlay network.图3 叠加网络示例
(1)
为满足位置邻近关系的时间依赖特征,式(1)引入了衰减思想,以保证距离当前时间较近的邻近关系对叠加网络的权重影响较大.
图3为图1的叠加网络实例.由于叠加网络为无向图,故wi j=wj i.
密度(density)是用来衡量社会网络中不同结点之间聚集程度的重要指标之一.我们利用该指标度量叠加网络中子图的聚集程度.
定义4. 聚集密度.若S为叠加网络G中的任意一子图,|US|和|ES|分别为S拥有的结点数和链接数,dens(S)为S的聚集密度,则有:

(2)
其中,nS=(|US|×(|US|-1))/2,表示S中的最大链接数.
根据聚集密度,可提取叠加网络中聚集程度较为紧密的最大子图,称之为极大紧密子图(maximal close subgraph).
定义5. 极大紧密子图.设ε为给定聚集密度阈值,S为G中的任意子图且|US|≥2,若称S为极大紧密子图,当且仅当2个条件同时满足:
1)den(S)≥ε;
2) 对于任意v∈U且v∉S,e={ev u|u∈S},den(S∪(v,e))<ε成立,即在S中加入新结点v及其相连的边e后,所形成子图的聚集密度小于ε.
因此,极大紧密子图中包含了聚集关系较为密切的结点.
根据观察,在学术会议离线网络中,多个用户发生位置邻近的可能性主要有:1)共同去参加感兴趣的学术报告或分组讨论;2)新旧朋友聚在一起聊天交流、喝咖啡或用餐.因此,相对于研究兴趣不相同的会议代表,研究兴趣相同的代表发生位置邻近的频率较高且时间较长.同样,相对于非朋友关系的代表,具有朋友关系的代表发生位置邻近的频率较高且时间较长.因此,总体上,具有相同研究兴趣的代表和具有朋友关系的代表更易于在叠加网络中形成极大紧密子图.因此,我们可推测:存在于一个极大紧密子图的会议代表在未来发生位置邻近的可能性较大,即可将离线瞬态社会网络中的多用户邻近预测问题转化为从叠加网络中挖掘极大紧密子图问题.
本研究的预测策略为:在当前叠加网络中,属于一个极大紧密子图中的用户将在下一个时间段可能发生位置邻近.
定义6. 多用户邻近预测.G是由n个连续网络片段{g1,g2,…,gn}形成的叠加网络.若S为G中的极大紧密子图,则预测S中的用户在第n+1个网络片段gn+1中将发生位置邻近.
2 预测总体框架
根据上述定义,首先给出多用户邻近预测的总体框架,如图4所示:

Fig. 4 The overall framework of multi-user proximity prediction.图4 多用户邻近关系预测总体框架
从图4可以看出,多用户位置邻近关系预测包括4个步骤:
步骤1. 收集网络片段.首先,将短距离通信设备探测到的相遇关系按给定时间段进行划分;然后,对每个划分进行统计,生成网络片段g1,g2,…,gn,其中每个片段包括用户集、邻近边集及权重集.
步骤2. 网络叠加.将g1,g2,…,gn中的用户集和邻近关系集进行叠加,并按照式(1)计算每条边的叠加权重,从而得到叠加网络G.
步骤3. 网络过滤.由于叠加网络中存在噪声邻近边,因此根据边权重阈值过滤G中的噪声关系.
步骤4. 极大紧密子图发现.对过滤后得到的每个独立网络子图,计算其聚集密度,判断其是否为极大紧密子图.若是,则预测该子图中的用户在下一个时间片段发生位置邻近;若不是,则对子图进行分裂,直到剩余结点为孤立结点.
3 构建叠加网络
叠加网络是进行预测的基础,在挖掘最大紧密子图之前,需要构建叠加网络.
OffESN中的位置邻近信息随着时间的增长不断增加.在预测开始时,我们选取前n个网络片段进行叠加网络初始化.初始化过程如算法1所示:
算法1. 叠加网络初始化.
输入:{g1,g2,…,gn};
输出:叠加网络G=(U,E,W).
①k=1;
②U=∅,E=∅;
③ for eachuiinUk(k=1,2,…,n)
④U=ui∪U; /*合并结点集*/
⑤ end for
⑥ for eachei jinEk(k=1,2,…,n)
⑦E=ei j∪E; /*合并边集*/
⑧ end for
⑨ for eachei j∈Edo
⑩ setwi j=0; /*初始化边的权重*/



衰减公式计算*/

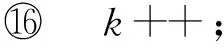


初始化之后,每次只需将新时间片段产生的边及结点添加到叠加网络中,同时更新边的权重,以获得最新叠加网络.
4 极大紧密子图发现
本研究拟通过发现极大紧密子图来判断网络中多用户是否位置邻近.但是,由于事先无法知道不同时刻叠加网络中极大紧密子图数量及每个子图中的用户数量,因此拟采用基于分裂的思想发现极大紧密子图.
GN算法[18]是一种分裂型的社区发现算法.该算法根据网络中社区内部高内聚、社区之间低内聚的特点,逐步去除社区之间的边,以得到相对内聚的社区结构.该算法按边介数大小随机删除边进行网络结构分裂,无需在执行算法之前指定子图目标个数及规模.但是,利用GN算法不能直接用于极大紧密子图提取,其原因主要有:
1) GN算法是为静态无权图设计,它是将边介数作为网络分裂的依据,而未考虑边的权重、图的结构和权重的动态变化;
2) 该算法是为社区发现而设计,网络分裂终止条件为社区模块度Q,未考虑离线瞬态社会网络中叠加网络特征.
针对以上问题及OffESN特征,我们在进行网络分裂时做了3点扩充:
1) 为支持OffESN的动态特征,实时更新叠加网络中的结点、边及权重;
2) 利用加权边介数代替边介数作为网络分裂的依据,即每次选取加权边介数最大的边删除;
3) 利用聚集密度作为网络分裂的终止条件,即当分裂子图的聚集密度大于阈值时停止分裂.
4.1 加权边介数
边介数(edge betweenness,EB)是用来衡量边在网络中重要性程度的度量指标,它表示网络中所有最短路径中经过一条边的路径数目占最短路径总数的比例.边介数值较高的边,它们最有可能占据连接不同子网络的“桥”位置[18].例如,图3中边e26具有较高的边介数,因为它连接了分别由用户1~5和用户6~9组成的2个子网络.
定义7. 边介数.边介数为网络中所有最短路径中经过一条边的路径数量占全部最短路径数量的比例.设EB(ei j)为边ei j的边介数,其计算为
(3)
其中,σ(s,t)为从结点s到结点t的最短路径数量,σ(s,t|ei j)为从结点s到结点t经过边ei j的最短路径数.
由于叠加网络中的邻近关系具有权重,故其为无向有权图.为保证重要的边(具有较高权重的边)不被轻易删除,于是提出加权边介数(weighted edge betweenness,WEB)概念.
定义8. 加权边介数.加权边介数为一条边的边介数与该边权重的比值.设WEB(ei j)为ei j的加权边介数,其计算为

(4)
4.2 极大紧密子图发现算法
由于短距离通信技术的不稳定性,可能存在噪声数据,故在进行挖掘极大紧密子图之前,需先去除叠加网络中权重小于指定阈值的边,然后再进行分裂.算法2是极大紧密子图发现算法描述.
算法2. 极大紧密子图发现算法.
输入:叠加网络G=(U,E,W)、边权重阈值θ.
① for eachei jinEdo /*网络过滤*/
② ifwi j<θ
③delete(ei j,G); /*删除权重小于权重阈值θ的边*/
④ end if
⑤ end for
⑥split(G). /*网络分裂*/
网络分裂函数split(G)是极大紧密子图发现算法的核心.当网络聚集密度小于阈值ε时,则去除加权边介数最大的边,将网络分裂为2个子网络.当网络只有1个结点或其聚集密度大于阈值ε时,则停止分裂.算法3为网络分裂算法.
算法3. 网络分裂算法split(G).
输入:待分裂的网络G=(U,E,W);
输出:极大紧密子图集合.
① if |U|=1
②remove(G);
③ end if
④dens(G)=|EG|/nG; /*计算G的聚集密度*/
⑤ ifdens(G)>ε
⑥ returnG;
⑦ else
⑧ for eachei jinEdo

⑩ end for






极大紧密子图发现算法的核心是计算边的加权边介数.设图中结点数为n,边数为m,则计算单条边加权边介数的时间复杂度为O(mn).因此,在最差情况下,对于具有m条边的图而言,极大紧密子图发现算法的时间复杂度为O(m2n).
5 实验及结果分析
5.1 实验准备
本实验采用的2个数据集sigcomm 2009[17]和mobility 2011[19]均来自CRAWDAD网站.我们分别从这2个数据集中提取12 153和1 339条邻近关系记录.2个数据集均以天为时间段进行网络片段划分,并以位置邻近的频率数作为边权重.
本实验所选择的性能评价指标为预测准确率(precision rate,PR)和召回率(recall rate,RR).设X为预测的多用户邻近关系数,Y为在第n+1个网络片段中实际多用户邻近关系数,Z为X中实际包含的多用户邻近关系数,则有:PR=ZX;RR=ZY.
本文所提出的多用户邻近关系预测策略(记为MPP)是基于分裂思想进行极大紧密子图提取.由于尚未见离线瞬态社会网络多用户邻近预测算法,故拟选择采用相似的分裂思想进行社区发现的GN算法及Radicchi算法[20]进行比较.与GN算法不同的是,Radicchi算法引入了边聚集系数进行网络分裂,减低了算法的时间复杂度,但当网络中三角环数量较少时准确率会下降.对于社区发现算法,我们预测位于相同社区中的多个用户在下一个时刻可能相遇.
本实验的硬件环境为处理器Intel®Xeon®CPU E5645@2.40 GHz、内存4 GB,操作系统为Windows 7.

Fig. 5 Influence of the weight threshold on precision rates.图5 权重阈值对准确率的影响
5.2 实验结果及分析
实验1. 边权重阈值对准确率和召回率的影响.
图5显示了不同边权重阈值θ下(固定ε=0.6)多用户邻近关系预测结果.可以看出,当边权重阈值较小时,2个数据集精确度都不高.从sigcomm 2009数据集的结果可以看出,当θ从0.04增加到0.10时,准确率略微上升后基本保持不变;当θ从0.06增加到0.10时,mobility 2011数据集的精确度整体变化不大.图6为召回率变化情况,总体趋势与图5相同.

Fig. 6 Influence of the weight threshold on recall rates.图6 权重阈值对召回率的影响
实验2. 聚集密度阈值对准确率和召回率的影响.
图7和图8展示了在不同聚集密度阈值ε下(固定θ=0.06)预测准确率和召回率的变化情况.

Fig. 7 Influence of the density threshold on precision rates.图7 聚集密度阈值对准确率的影响
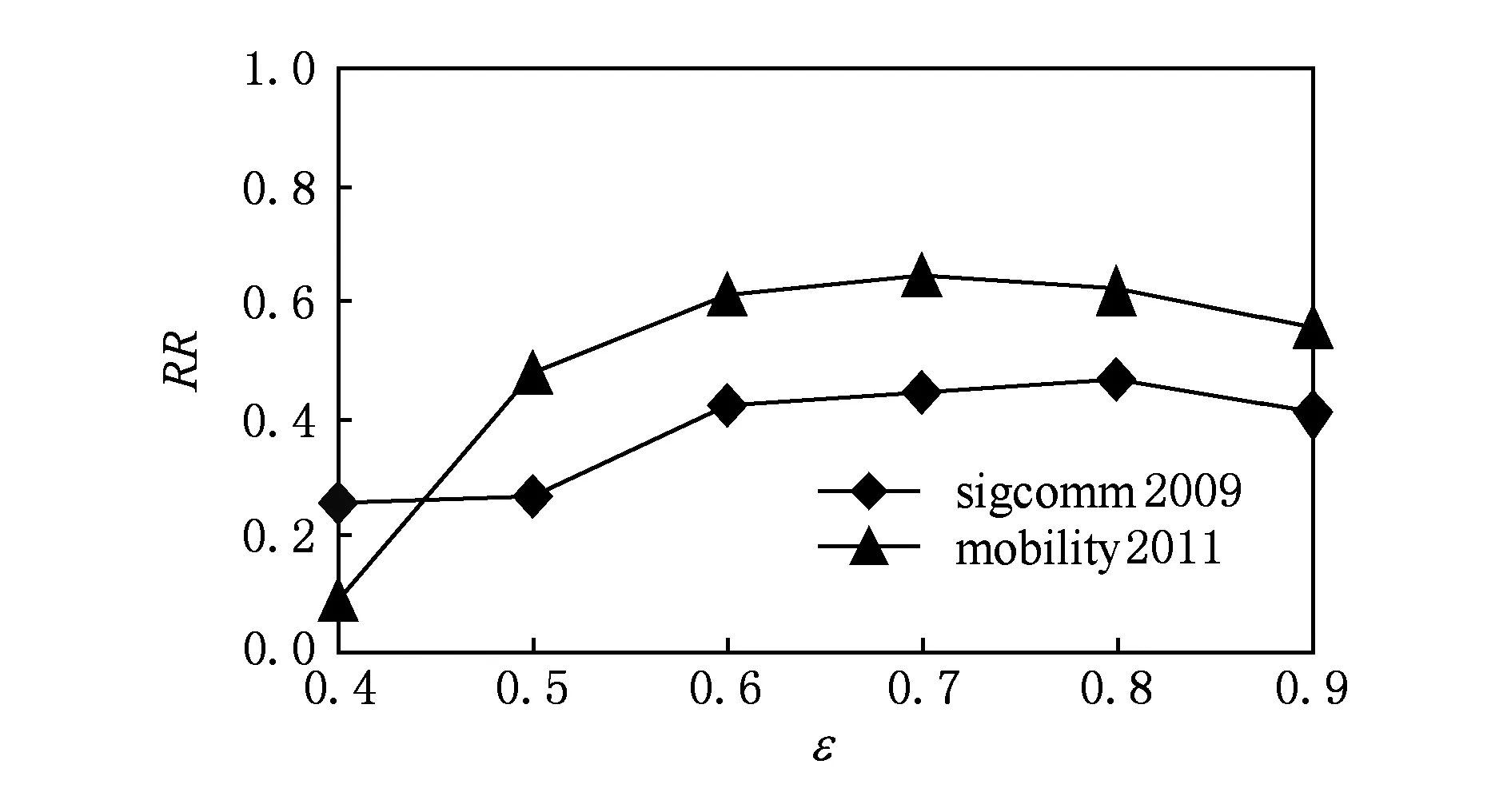
Fig. 8 Influence of the density threshold on recall rates.图8 聚集密度阈值对召回率的影响
从图7和图8可以看出,当ε从0.4变化到0.6时,2个数据集的准确率和召回率都呈上升趋势;而当ε达到 0.6时,2个指标的变化不大.这是由于当ε较大时,极大紧密子图规模相对较小,指标值变化相对固定.
实验3. 加权边介数对准确率和召回率的影响.
图9和图10展示了固定θ=0.06,ε=0.6时,分别利用加权边介数(WEB)和普通边介数(EB)作为分裂依据时的准确率和召回率比较.可以看出,采用加权边介数的准确率和召回率均高于采用普通边介数的准确率和召回率,其原因是加权边介数考虑了边的权重,避免了邻近关系较为紧密的边被删除.

Fig. 9 Influence of edge betweennesses on precision >rates.图9 边介数对准确率的影响

Fig. 10 Influence of edge betweennesses on recall rates.图10 边介数对召回率的影响

Fig. 11 Precision rate comparison of different algorithms.图11 不同算法准确率比较
实验4. 比较不同算法对准确率和召回率的影响.
图11和图12分别是3种算法预测的准确率和召回率的比较结果,其中固定θ=0.06,ε=0.6.

Fig. 12 Recall rate comparison of different algorithms.图12 不同算法召回率比较
可以看出,MPP算法的准确率和召回率都高于GN算法和Radicchi算法.在学术会议的离线网络中,每次同时发生位置邻近的用户数通常不多(常常几个人碰面在一起交流和讨论);而社区发现算法发现的社区规模往往较大,不易发现规模比较小的多用户位置邻近,故它们的准确率和召回率都比MPP算法低.
实验5. 分析不同算法的挖掘时间开销.
图13是3种算法的挖掘时间开销比较结果.可以看出,MPP算法所需时间开销小于GN算法,其原因是GN算法计算分裂终止判断条件——模块度的时间开销高于MPP算法计算聚集密度的开销.但是,由于Radicchi算法只需计算局部边聚集系数作为分裂条件,故其所需时间最少.

Fig. 13 Time overhead comparison of different algorithms.图13 不同算法的时间开销比较
6 结 论
本文针对离线瞬态社会网络中的多用户邻近关系预测问题展开研究,主要创新之处在于考虑了离线瞬态社会网络特征,提出了极大紧密子图概念及其挖掘策略,能有效地解决多邻近关系数及规模不确定问题.全文主要工作总结如下:
1) 设计了离线瞬态社会网络中多用户邻近关系预测的总体框架;
2) 考虑到用户邻近关系的强度不同,提出了采用加权边介数作为网络分裂依据,以避免重要边不被删除;
3) 提出了基于分裂思想的极大紧密子图提取算法;
4) 在真实数据集上进行了性能测试,测试结果验证了所提出算法的可行性.
在后续的研究中,我们将进一步研究离线瞬态社会网络的特征,以期发现更多特征指标及更有效的算法帮助提高预测的准确率.
[1]Kong Xiangnan, Zhang Jiawei, Yu P S. Inferring anchor links across multiple heterogeneous social networks[C] //Proc of the 22nd ACM Int Conf on Information & Knowledge Management (CIKM 2013). New York: ACM, 2013: 179-188
[2]Chin A, Wang Hao, Xu Bin, et al. Connecting people in the workplace through ephemeral social networks[C] //Proc of the 3rd IEEE Int Conf on Privacy, Security, Risk and Trust and Social Computing. Piscataway, NJ: IEEE, 2011: 527-530
[3]Chin A, Zhang Daqing. Ephemeral social networks[M] //Mobile Social Networking. Berlin: Springer, 2014: 25-64
[4]Zhuang Honglei, Chin A, Wu Sen, et al. Inferring geographic coincidence in ephemeral social networks[M] //Machine Learning and Knowledge Discovery in Databases. Berlin: Springer, 2012: 613-628
[5]Scholz C, Atzmueller M, Stumme G. On the predictability of human contacts: Influence factors and the strength of stronger ties[C] //Proc of the 4th IEEE Int Conf on Privacy, Security, Risk and Trust and Social Computing. Piscataway, NJ: IEEE, 2012: 312-321
[6]Liao Guoqiong, Zhao Yuchen, Xie Sihong, et al. An effective latent networks fusion based model for event recommendation in offline ephemeral social networks[C] //Proc of the 22nd ACM Int Conf on Information & Knowledge Management(CIKM 2013). New York: ACM, 2013: 1655-1660
[7]Liben-Nowell D, Kleinberg J. The link-prediction problem for social networks[J]. Journal of the American Society for Information Science and Technology, 2007, 58(7): 1019-1031
[8]Lichtenwalter R N, Lussier J T, Chawla N V. New perspectives and methods in link prediction[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (KDD 2010). New York: ACM, 2010: 243-252
[9]Bliss C A, Frank M R, Danforth C M, et al. An evolutionary algorithm approach to link prediction in dynamic social networks[J]. Journal of Computational Science, 2014, 5(5): 750-764
[10]Hasan M A, Chaoji V, Salem S, et al. Link prediction using supervised learning[C] //Proc of the 6th SIAM Int Conf on Data Mining: Workshop on Link Analysis, Counter-terrorism and Security. Philadelphia, PA: SIAM, 2006: 531-540
[11]Benchettara N, Kanawati R, Rouveirol C. Supervised machine learning applied to link prediction in bipartite social networks[C] //Proc of 2010 IEEE/ACM Int Conf on Advances in Social Networks Analysis and Mining. Los Alamitos, CA: IEEE Computer Society, 2010: 326-330
[12]Wang Chao, Satuluri V, Parthasarathy S. Local probabilistic models for link prediction[C] //Proc of the 7th IEEE Int Conf on Data Mining (ICDM 2007). Los Alamitos, CA: IEEE Computer Society, 2007: 322-331
[13]Kashima H, Abe N. A parameterized probabilistic model of network evolution for supervised link prediction[C] //Proc of the 6th IEEE Int Conf on Data Mining (ICDM 2006). Los Alamitos, CA: IEEE Computer Society, 2006: 340-349
[14]Lü Linyuan. Link prediction on complex networks[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(5): 651-661 (in Chinese)
(吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报, 2010, 39(5): 651-661)
[15]Huang Zan, Lin D K J. The time-series link prediction problem with applications in communication surveillance[J]. INFORMS Journal on Computing, 2009, 21(2): 286-303
[16]Silva Soares da P R, Cavalcante Prudencio R B. Time series based link prediction[C] //Proc of the 6th Int Joint Conf on Neural Networks. Piscataway, NJ: IEEE, 2012: 1-7
[17]Pietilainen A K, Diot C. The thlab/sigcomm2009 dataset[EB/OL]. (2012-07-15)[2015-02-20]. https://crawdad.cs.dartmouth.edu/thlab/sigcomm2009/20120715
[18]Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821-7826
[19]Ciobanu R I, Dobre C. The upb/mobility2011 dataset[EB/OL]. (2012-06-18)[2015-02-20]. http://www.crawdad.org/upb/mobility2011 /20120618
[20]Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of Sciences, 2004, 101(9): 2658-2663

Liao Guoqiong, born in 1969. PhD. Professor at the School of Information Technology, Jiangxi University of Finance and Economics. Senior member of China Computer Federation. His main research interests include database, data mining and social networks.

Wang Tingli, born in 1990. Master from the School of Information Technology, Jiangxi University of Finance and Economics. Her main research interests include data mining and social networks.

Deng Kun, born in 1980. PhD candidate at the School of Information Technology, Jiangxi University of Finance and Economics. His main research interests include data mining and social networks.

Wan Changxuan, born in 1962. PhD. Professor and PhD supervisor at the School of Information Technology, Jiangxi University of Finance and Economics. Senior member of China Computer Federation. His main research interests include Web data management and Web information retrieval.
Multi-User Location Proximity Prediction in Offline Ephemeral Social Networks
Liao Guoqiong1,2, Wang Tingli1, Deng Kun1,2, and Wan Changxuan1,2
1(SchoolofInformationTechnology,JiangxiUniversityofFinanceandEconomics,Nanchang330013)2(JiangxiProvinceKeyLaboratoryofDataandKnowledgeEngineering(JiangxiUniversityofFinanceandEconomics),Nanchang330013)
Offline ephemeral social network (OffESN) is defined as a new kind of offline social networks created at a specific location for a specific purpose temporally, and lasting for a short period of time. With the popularity of mobile intelligent terminals and the development of short distance communication technologies such as Bluetooth and RFID, the OffESN is receiving more and more attentions from industry and academic communities. Location proximity relations are encounter relations of the users in the OffESN. Aiming to the characteristics such as dynamic change and short duration time, this paper intends to study the problem of multi-user location proximity in the OffESN. First of all, the paper puts forward relevant concepts in the OffESN and defines the problem to be solved. Then, it designs the overall framework of multi-user location proximity prediction, including network segments collection, overlay networks construction, network filter and maximal close subgraphs discovery. Based on the framework and the splitting idea, the paper suggests a maximal close subgraph discovery algorithm for predicting multi-user location proximity. The algorithm uses weighted edge betweenness (WEB) as the basis of splitting, and uses the aggregate density as the termination condition of spitting, which can effectively solve the problem that both numbers of location proximity relations and the users in each location proximity are uncertain. Finally, the experiments on two real datasets verify the feasibility and efficiency of the suggested prediction strategy.
social networks; ephemeral social networks; location proximity; maximal close subgraphs; link prediction
2015-05-21;
2016-02-16
国家自然科学基金项目(61262009);江西省自然科学基金项目(20151122040083);江西省优势科技创新团队建设计划项目(20113BCB24008)
TP18
This work was supported by the National Natural Science Foundation of China (61262009), the Natural Science Foundation of Jiangxi Province (20151122040083), and the Jiangxi Foundation of Superiority Science and Technology Innovation Team Building Program (20113BCB24008).

