基于样本权重的不平衡数据欠抽样方法
熊冰妍 王国胤 邓维斌
(重庆邮电大学计算智能重庆市重点实验室 重庆 400065)(1217185006@qq.com)
基于样本权重的不平衡数据欠抽样方法
熊冰妍 王国胤 邓维斌
(重庆邮电大学计算智能重庆市重点实验室 重庆 400065)(1217185006@qq.com)
现实世界中广泛存在不平衡数据,其分类问题是数据挖掘和机器学习的一个研究热点.欠抽样是处理不平衡数据集的一种常用方法,其主要思想是选取多数类样本中的一个子集,使数据集的样本分布达到平衡,但其容易忽略多数类中部分有用信息.为此提出了一种基于样本权重的欠抽样方法KAcBag(K-means AdaCost bagging),该方法引入了样本权重来反映样本所处的区域,首先根据各类样本的数量初始化各样本权重,并通过多次聚类对各个样本的权重进行修改,权重小的多数类样本即处于多数类的中心区域;然后按权重大小对多数类样本进行欠抽样,使位于中心区域的样本较容易被抽中,并与所有少数类样本组成bagging成员分类器的训练数据,得到若干个决策树子分类器;最后根据各子分类器的正确率进行加权投票生成预测模型.对19组UCI数据集和某电信运营商客户换机数据进行了测试实验,实验结果表明:KAcBag方法使抽样所得的样本具有较强的代表性,能有效提高少数类的分类性能并缩小问题规模.
不平衡数据;欠抽样;样本权重;聚类;集成学习
不平衡数据集是指在数据集中某一类的样本数量远远少于其他类的样本数量,其中数量占多数的类称为多数类,而占少数的类称为少数类.不平衡数据集的分类问题大量存在于人们的现实生活和工业生产之中,如客户流失预测[1]、DNA微阵列数据分析[2]、软件缺陷预测[3]、垃圾邮件过滤[4]、文本分类[5]、医疗诊断[6]等,在这些应用中少数类分类精度往往更为重要.因此,提高少数类的分类精度成为不平衡数据集中的研究重点.
现有的不平衡数据处理方法主要分2类:
1) 从训练集入手,通过改变训练集样本分布,降低不平衡程度.常用的抽样方法有2种:过抽样和欠抽样.过抽样是通过增加训练集中少数类的数量,使数据集的样本分布达到平衡,如SMOTE(synthetic minority over-sampling technique)算法[7],该方法通过插值生成新的人造样本,使少数类具有更大的泛化空间.Borderline-SMOTE算法[8]是一种改进的SMOTE算法,其只对少数类的边界样本进行过抽样处理,以保证新增加的样本是有价值的.欠抽样是通过减少多数类样本来使数据集的样本分布达到平衡,如单边选择(one-sided selection)算法[9],该方法采用单边采样方式,去除大类中的噪音样本、边界样本和冗余样本.SBC(under-sampling based on clustering)算法[10]通过聚类后簇内的正类与负类的比例确定抽样比例参数.
2) 从学习算法入手,根据算法在解决不平衡问题时的缺陷,适当地修改算法使之适应不平衡分类问题.常用策略有: 代价敏感方法,在传统的分类算法的基础上引人代价敏感因子,设计出代价敏感的分类算法,如代价敏感决策树[11]、代价敏感支持向量机[12]等;集成学习方法,使用一系列分类器进行学习,并使用某种规则把各个学习结果进行整合从而获得比单个学习器更好的学习效果,如bagging[13],AdaBoost[14],AdaCost[15]等.
此外,将欠抽样方法与集成学习进行融合,既能利用欠抽样的优点平衡数据集,使分类器能更好地提高少数类的分类性能,又能利用集成方法的优点提高不平衡数据集的整体分类能.文献[16]提出的EBBag(exactly balanced bagging)算法结合随机欠抽样和bagging算法,对于每次迭代,训练集由所有的少数类样本和从多数类样本中随机抽取的一个子集组成,但随机抽取多数类样本没有考虑数据的分布特点,容易丢失有用信息.RBBag(roughly balanced bagging)[16]算法是对EBBag算法的改进,其主要思想在于如何决定2类中样本采样的数目:少数类样本采样的数目等于原子集样本的数目,而多数类样本采样数据取决于其二项分布,该算法的优点在于它既保留了初始背包技术的优点,同时还使得少数类样本的有用信息得到充分利用,因此较一般的背包技术鲁棒性更强.文献[17]提出的uNBBag0.5(under-sampling neighbourhood bagging)算法是通过统计各样本周围的多数类样本数来计算其样本权重,并根据权重对原始数据集进行欠抽样,使分类器性能得到较大提升,但其只着重研究了少数类的样本权重,所有多数类样本的权重相同,未考虑样本间的分布差异.将过抽样技术与bagging算法相结合也是一种有效提高分类性能的方法,如oNBBag2(over-sampling neighbourhood bagging)算法[17]、OvBag(over-sampling bagging)算法[18]、SmBag(SMOTE bagging)算法[18].
基于以上研究,本文通过研究多数类样本的分布情况提出一种基于样本权重的不平衡数据欠抽样方法KAcBag(K-means AdaCost bagging),首先根据原始数据集中各类样本的数量初始化各样本的权重,然后通过K-means聚类算法对数据集进行多次聚类,并根据每次的聚类结果更新样本权重,最后按照样本权重的大小对多数类样本进行欠抽样得到平衡的训练集,以决策树作为bagging算法的基分类器,新的测试样本的类别由多个基分类器投票表决.
1 相关理论
1.1K-means聚类算法
MacQueen[19]在1967年提出了K-means算法,它是广泛应用于科学和工业诸多聚类算法中有效的算法之一.K-means算法的工作机理是把n个样本点分为k个簇,各簇内的样本点具有较高的相似性,而各簇间的样本点相似程度较低.如算法1所示.
算法1.K-means聚类算法.
输入:样本数据集、簇的个数k、最大迭代次数;
输出:k个簇.
Step1. 在样本数据集中随机选择k个样本点作为初始簇中心;
Step2. 在第i次迭代中,对任意一个样本,求其到k个中心的距离,将该样本归到距离最短的中心所在的簇;
Step3. 使用每个簇内的样本均值作为新的簇中心;
Step4. 对于所有的k个簇中心,如果利用Step2和Step3的迭代法更新后,目标函数达到最优或达到最大迭代次数,则迭代结束,否则继续迭代;
Step5. 结束,得到k个簇.
采用欧氏距离作为距离度量方法,其计算公式为
(1)
其中,xi和yi分别代表数据x的第i维和数据y的第i维.
目标函数为最小化样本到其簇中心的距离的平方和,其计算公式为
(2)
其中,E是数据集中所有样本的误差平方和,c是给定的样本,ci是簇的中心.
1.2 AdaCost算法
AdaCost算法是Fan于1999年为改进AdaBoost算法而提出[15],其主要思想是给每一个训练样本分配一个权重,并通过不断修正权重来实现推进(boosting)训练.分配初始权重后,用一个弱分类算法在训练集上进行训练,训练后得到一个弱分类器,同时对样本权重进行调整,训练失败的样本权重增大,训练成功的样本权重减少,使分类算法能在下一轮训练中集中力量对训练失败的样本进行学习.权重更新后,算法在更新的训练集上继续训练,再调整样本权重,循环往复,从而得到一系列的弱分类器.这些弱分类器构成组合分类器,算法采用有权重的投票方式来产生最终预测结果.
AdaCost算法的权重更新公式为
(3)

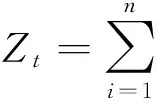
1.3 bagging算法
bagging 是一种基于组合的元学习算法,其基本思想是是给定一个弱学习算法和一个训练集S,让该学习算法训练T轮,每轮的训练集由从初始的训练集中随机取出的n个训练样本组成,每个训练样本在某轮训练集中可以出现多次或根本不出现.训练T轮之后可得到一个预测函数序列h1,h2,…,ht,最终的预测函数h*对分类问题采用投票方式对测试样本进行判别.
2 基于样本权重的欠抽样方法
欠抽样是一种有效处理不平衡数据的方法,但在抽样过程中可能丢失一些具有较强判别性的样本,为了弥补这一缺点,本文通过引入样本权重来反映样本所处区域,旨在找出位于多数类中心区域的样本,增大强判别性样本被选中的概率.bagging方法是一个复合模型,它由多个分类器通过投票返回预测的类标号,可以大幅度提高基分类器的准确率,鉴于每个基分类器的性能不同,本文对各基分类器赋予权重来反映其对最终结果的贡献程度.KAcBag方法主要包括样本权重的确定与分类器加权投票2部分.
2.1 样本权重的确定
具体思路为: 首先根据原始数据集中各类样本的数量初始化各个样本的权重;然后通过K-means聚类算法对数据集进行多次聚类,根据每次聚类的结果对各个样本的权重进行修改,若样本的类别与其所在簇的类别一致则权重减少,若两者类别不一致则权重增大,且权重变化的幅度与其当前权重的大小成正比;最后所得权重小的多数类样本即位于多数类的中心区域,具体过程如算法2所示.
算法2. 样本权重的确定.
输入:带类标记的训练数据集D、聚类次数K、第1次聚类簇的个数N、簇减少的个数n;
输出:一个带权重的数据集.
Step1. 根据D中每类样本的个数给各个样本赋予权重,正类样本数为p,负类样本数为q,所有正类样本权重为1/2p,负类样本权重为1/2q;
Step2. 用K-means算法对训练集D进行聚类,形成N个簇;
Step3. 计算每个簇的类别标记:分别计算每个簇内正负类样本的权重和,取权重和大的类为簇的类标记;
Step4. 根据聚类结果修改各个样本的权重,类标记与簇的类标记相同则权重减小,不同则增大;
Step5. 若聚类次数小于K,修改聚类簇的个数N=N-n,并转Step2;
Step6. 返回一个带权重的数据集.
其中,修改权重的方法以AdaCost算法的权重更新公式为基础,用样本的当前权重替代其代价调整函数里的ci,即样本的当前权重为样本的误分代价,代价调整函数定义如下:
(4)
2.2 分类器加权投票
在确定训练集中各样本的权重之后,按权重大小对多数类样本进行抽样,得到与少数类样本数相同的多数类样本;然后将抽样所得样本与所有少数类样本组合成一个平衡的训练集,作为bagging成员分类器的训练数据;最后根据以每个分类器的正确率作为权值,进行加权投票.但是因为按权重大小抽样,权重越大的样本被抽中的概率越大,本文旨在多抽取位于中心区域的样本,而根据2.1节的权重确定算法所得的结果,权重小的样本处于中心区域,所以在对多数类进行抽样之前,需要对所有多数类样本的权重进行一次求倒运算,使权重小的样本变为权重大的样本.具体过程如算法3所示.
算法3. 分类器加权投票.
输入: 带权重和类标记的训练数据集D、测试数据集T、子分类器的个数K;
输出: 带预测类标记的数据集.
Step1. 对D中所有多数类样本的权重进行求倒计算;
Step2. 按权重对D中的所有多数类样本进行有放回抽样,与所有少数类样本组成一个平衡的数据集Di;
Step3. 使用决策树算法对Di进行学习,得到预测函数hi;
Step4. 若分类器个数小于K,转Step2;
Step5. 使用预测函数序列h1,h2,…,hk对T中的每个样本进行投票表决.
其中,每个预测函数的表决权重为
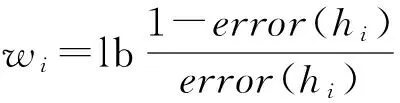
error(hi)为预测函数hi的错误率,即hi误分Di中每个样本的权重和,其计算公式为
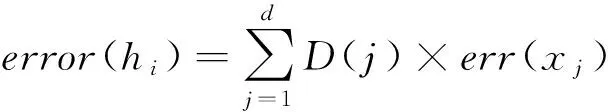
3 实验与分析
3.1 分类的评价方法
传统的分类器采用精度指标来衡量分类性能,但在不平衡数据集中,多数类样例个数远远多于少数类,传统分类算法预测会倾向于多数类,如把所有样例分为多数类,依然会获得很高的分类精度,但是却不能识别一个少数类,故分类精度不能正确反映不平衡数据集的分类结果.针对不平衡数据,很多学者提出F-measure[8],G-mean[20]等评价方法,其大多建立在混淆矩阵(如表1所示)的基础上.假设表1中正类和负类分别代表少数类和多数类,则TP和TN分别表示正确分类的少数样本和多数样本的个数,FP和FN分别表示误分类的少数类样本和多数类样本的个数.
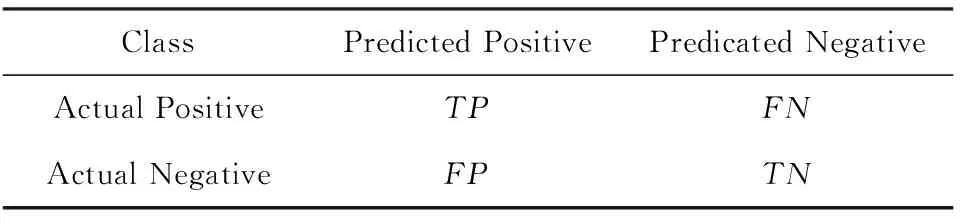
Table1 Confusion Matrix for Two-class Problem
F-measure是一种不平衡数据分类问题的评价准则,其定义[8]为
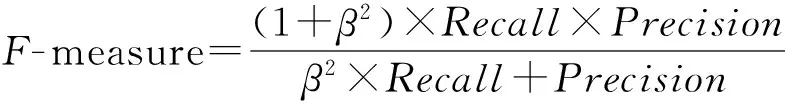
其中,Recall为查全率;Precision为查准率;β表示Precision与Recall的相对重要性,在本文实验中β=1.只有当查全率和查准率都较大时,F-measure才会相应地较大.因此,F-measure可以合理地评价分类器对于少数类的分类性能[21].即令:
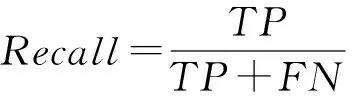

G-mean是一种衡量数据集整体分类性能的评价指标,其定义如下[20]:
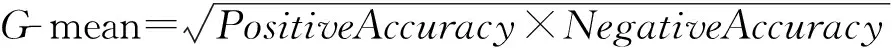
G-mean准则是在保持正、负类分类精度平衡的情况下最大化2类的精度.假定对负类的分类精度很高,而对正类的分类精度很低,则会导致低的G-mean值,而只有当两者都较高时,才会得到高的G-mean值.因此,G-mean准则衡量的是数据集整体的分类性能[21].本文将使用F-measure,G-mean来衡量少数类及数据集整体的分类性能.
3.2 非参数统计检验方法
F-measure和G-mean是从单个数据集上衡量不同算法的分类性能,为了从整体上比较各种算法的性能优劣,本文将非参数统计检验方法中的Friedman检验[22]和Wilcoxon符号秩检验[22]引入到分类算法的性能评估中.
Friedman检验用于判断多种分类算法是否存在显著差异,其原假设是:多种分类算法无显著差异,具体检验步骤为:
1) 将各区组内数据由小到大分别编秩,遇相同数值取平均秩次;
2) 计算各分类算法的秩和Ri、平均秩;
3) 计算检验统计量:
3×n×(k+1),
其中,n是区组的数量,k是分类算法的数量;
4) 利用统计软件或查表确定P值,如果概率P值小于给定的显著性水平,则拒绝原假设,认为各分类算法之间存在显著差异,反之则不能拒绝原假设.
Wilcoxon符号秩检验是用于检验2种分类器算法之间是否存在明显差异问题,其具体检验步骤为: 1)计算2种分类器算法在每一组数据上的性能差值,并将差值的绝对值按从小到大的顺序编秩;2)计算秩和,令R1为第1个算法优于第2个算法的秩和,R2为第2个算法优于第1个算法的秩和;3)计算T值,T=min(R1,R2);4)根据所得T值查表或统计软件确定P值,若P小于给定的显著性水平,则认为2种算法具有显著差异.在本文中,使用SPSS软件来进行Friedman检验和Wilcoxon符号秩检验分析.
3.3 UCI数据
为了检验本文抽样方法的有效性,选择19组少数类和多数类样本比例不平衡的且具有不同实际应用背景的UCI数据*http://www.ics.uci.edu/~mlearn/ML Repository.html,对于含有多个类别的数据,选择数量最少的类作为少数类,并将其他类合并为一个大的多数类.各数据集的基本信息如表2所示,Ratio为数据集的不平衡程度,即Ratio等于多数类样本数除以少数类样本数.
为了使实验结果更具客观性,采用10折交叉验证的方法对分类效果进行验证,即将数据集中的数据随机等分为10份,依次取其中1份作为测试集,其余9份作为训练集,然后运行相应的分类方法对训练集中的数据进行分类学习,并用测试集进行测试,相应的10次测试结果的平均值作为1次10折交叉验证的结果.
在实验中,采用weka软件[23]中SimpleKMeans聚类算法对数据进行多次聚类,设聚类次数为6次,第1次聚类的簇的个数为训练集样本数的10%左右,簇减少的步长根据初始簇的个数和聚类次数确定,其取值需确保最后1次聚类的簇的个数大于0,weka软件中的J48决策树算法作为基分类器,算法参数使用软件中的默认参数设置.将实验结果与RBBag,OvBag,SmBag,oNBBag2,uNBBag0.5这5种bagging技术与抽样方法相结合的算法进行对比,表3和表4分别列出6种方法在19个UCI数据集上的少数类F-measure值和数据集整体的G-mean值,其中作为对比的5种算法的实验结果来自文献[17],表格中的最后一行为通过Friedman检验计算的各个算法的平均秩,其值越小证明算法的性能越好.表5列出了6种算法在F-measure和G-mean上两两进行Wilcoxon符号秩检验的结果(P值),显著性水平设置为0.05.
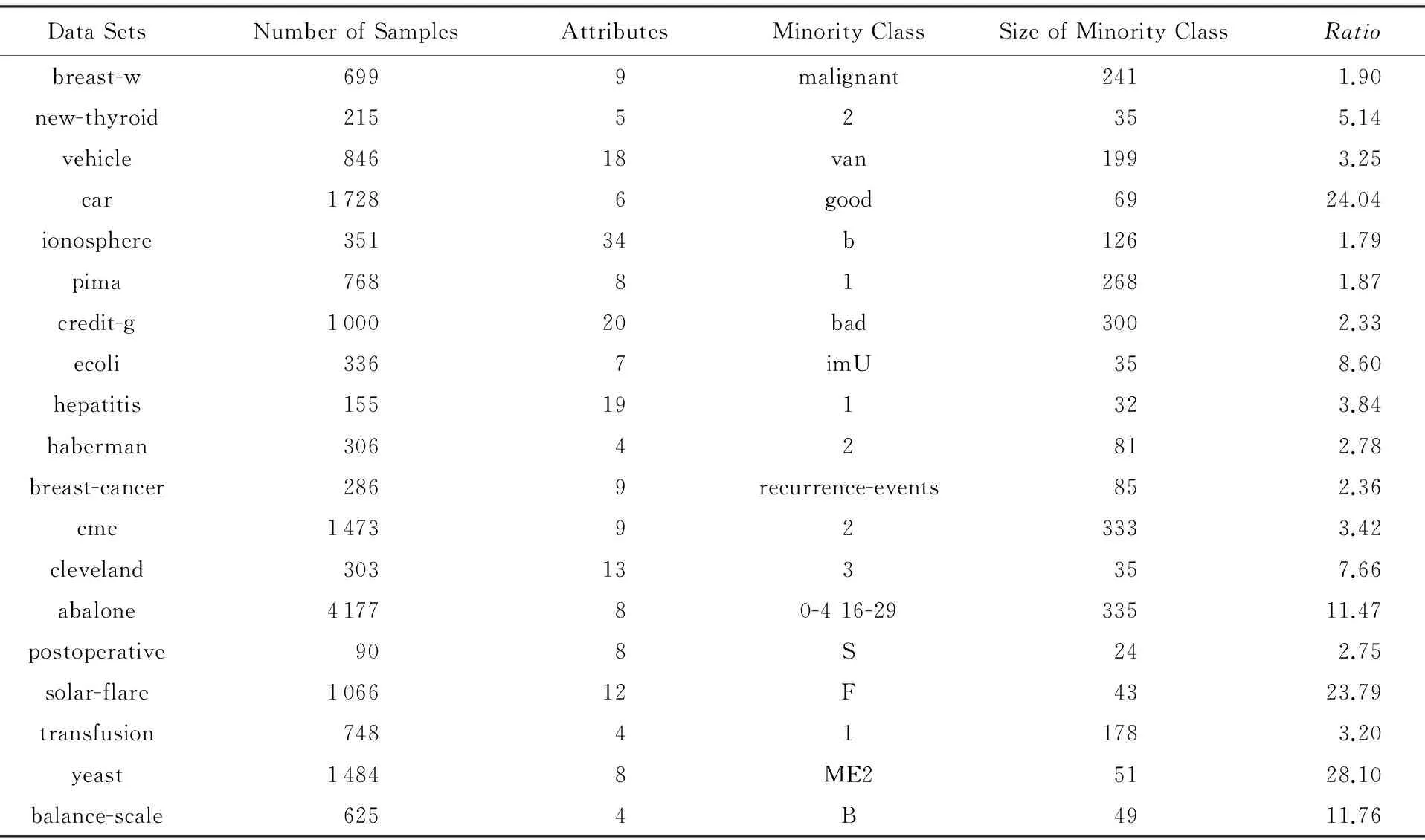
Table 2 Information of Data Sets
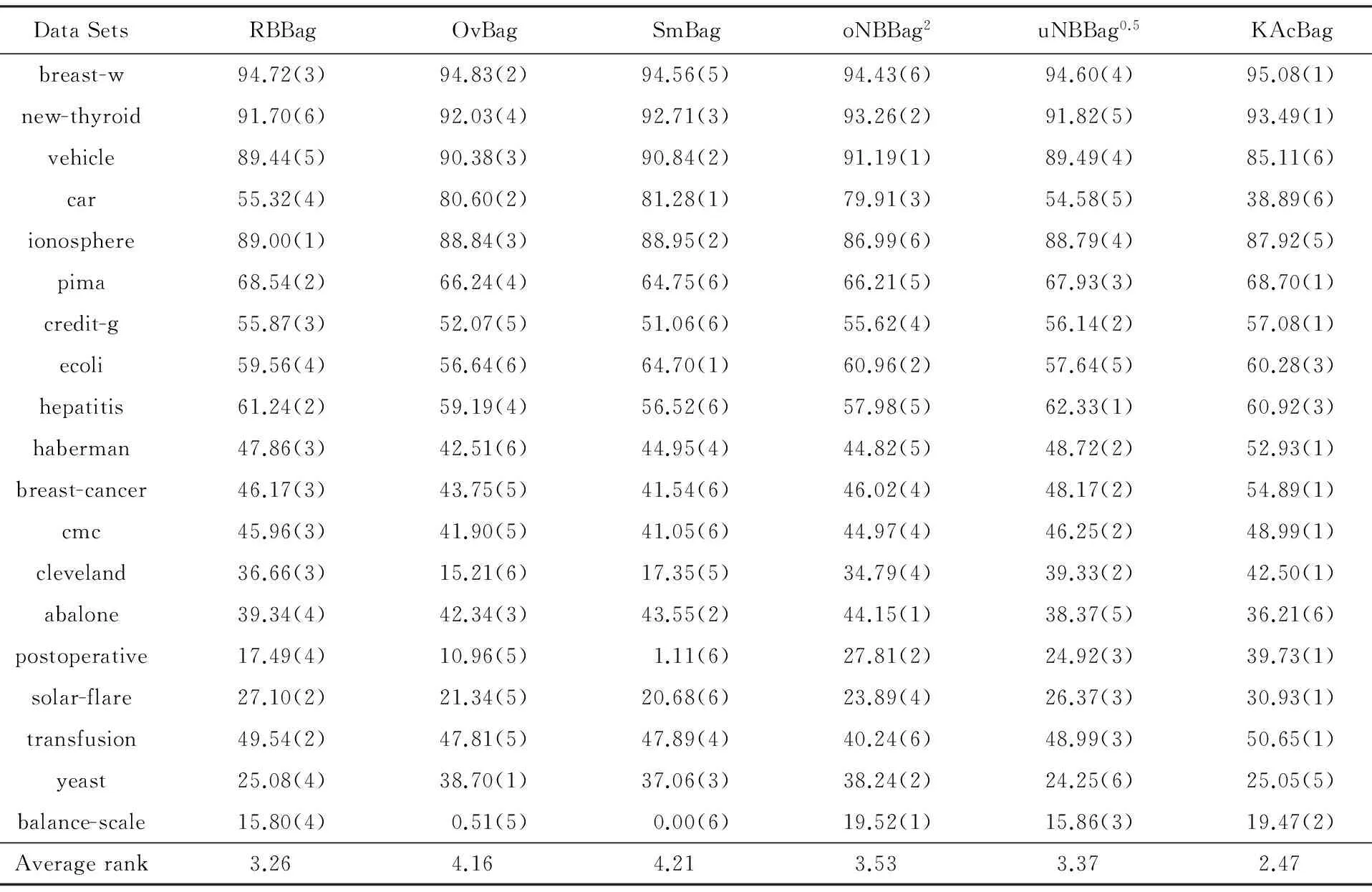
Table3 Minority Class F-measure Comparison of Different Sampling Algorithms
Note: The number between brackets represents the rank of the algorithm on this data set.

Table 4 Minority Class G-mean Comparison of Different Sampling Algorithms
Note: The number between brackets represents the rank of the algorithm on this data set.
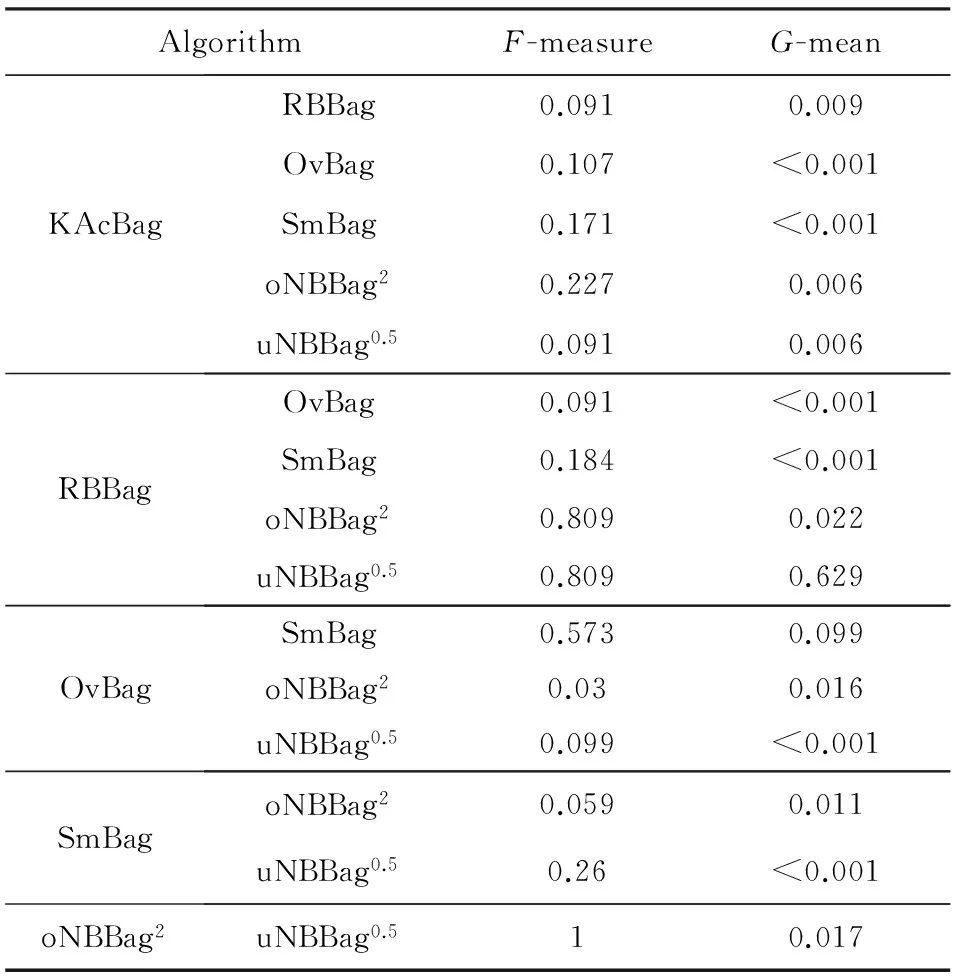
Table 5 The Wilcoxon Sign Rank Set for Pairwise Comparisons of Different Algorithms
由表3和表4可以看出,KAcBag算法在2个性能指标F-measure和G-mean上的平均秩最小,在breast-w,new-thyroid,credit-g,haberman,cleveland,breast-cancer,transfusion,postoperative,solar-flare,cmc上2个评价指标均优于其他算法,在pima,ecoli,abalone,yeast上有1个评价指标高于其他算法,并且另1个评价指标也是良好的,在ionosphere,hepatitis,balance-scale上评价指标略低于其他5种算法的最优值.对ecoli,abalone,yeast,balance-scale,car,vehicle这6个数据集,可以明显地看出过抽样方法的结果要优于欠抽样方法,这是因为数据集中少数类样本过少且不平衡程度较高,使得用欠抽样方法得到的平衡数据集丢失了过多的多数类样本,造成分类性能降低,本文方法虽在这类数据集上分类性能略低于OvBag,SmBag,oNBBag2这3种过抽样方法,但其在1个或2个评价指标上优于RBBag和uNBBag0.5这2种欠抽样方法.
从统计检验的角度来看,在F-measure上的Friedman检验结果为0.047,略小于显著性水平0.05,说明6种算法在此项指标上显著性差异不大.在G-mean上的Friedman检验结果小于0.001,说明6种算法在此项指标上有显著性差异,由表5的Wilcoxon符号秩检验结果可以明显看出,KAcBag算法在G-mean这项指标上效果优于其他5种算法(P<0.05),RBBag和uNBBag0.5算法无显著差异(P=0.629),但均优于另外3种欠抽样方法(P<0.05),3种欠抽样方法中以oNBBag2算法为最优.
为了观察聚类次数和簇减少的步长这2个参数的设定对KAcBag算法的影响,选择solar-flare数据集作为实验数据,它具有较高的不平衡比例和较大的样本个数.图1给出了当簇减少的步长为6且其他参数不变,聚类次数为3,6,9,12,15时,solar-flare数据集的F-measure值和G-mean值的变化情况.图2给出了当聚类次数为6且其他参数不变,簇减少的步长为3,6,9,12,15,18时,2个评价指标的变化趋势.
由图1和图2可知,在聚类次数和簇减少步长2个参数均设置合适的情况下,2个评价指标可以取得较好的结果.

Fig. 1 Effect of different clustering numbers on KAcBag.图1 不同聚类次数对KAcBag方法的影响
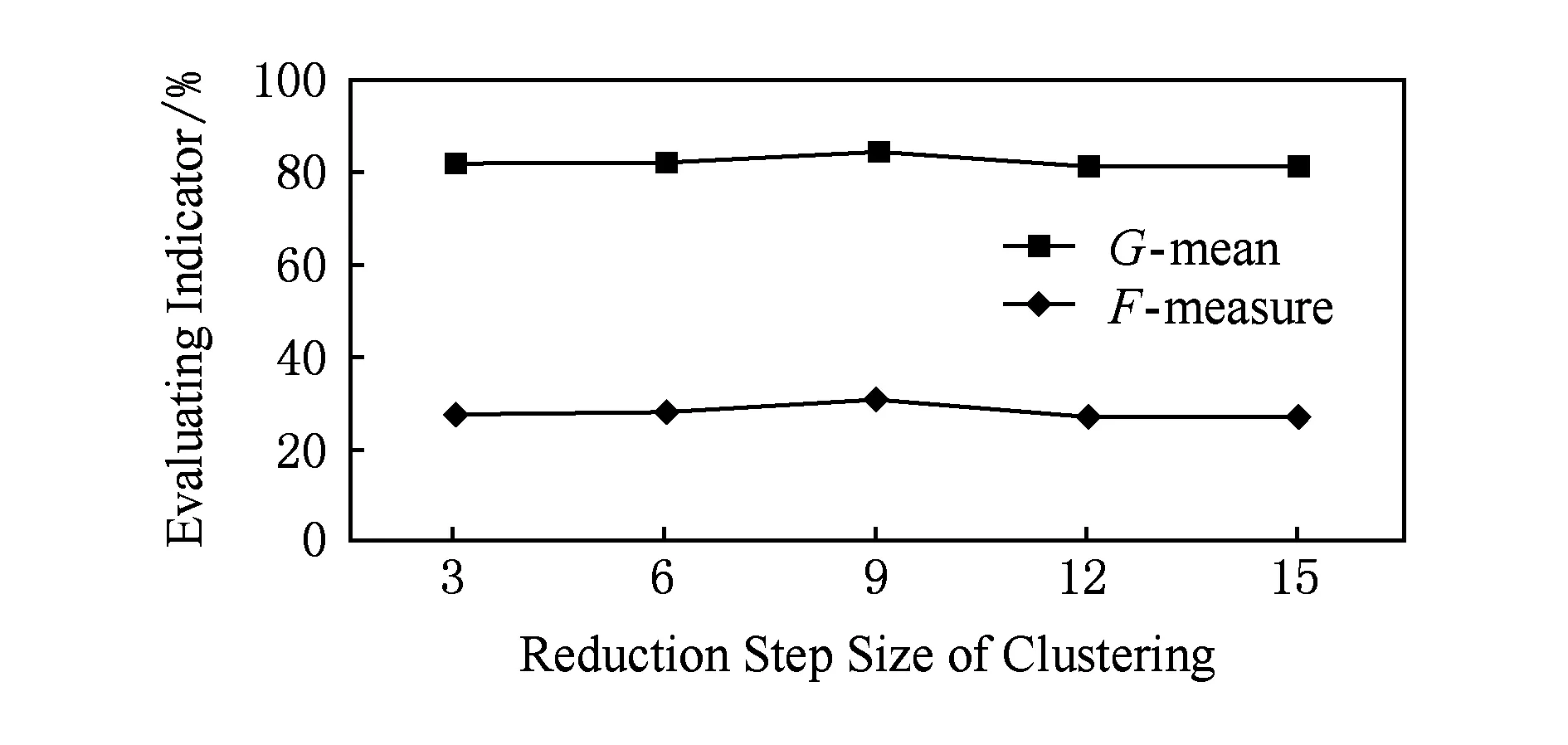
Fig. 2 Effect of different clustering reduction step size on KAcBag.图2 不同簇减少步长对KAcBag方法的影响
3.4 用户换机数据
在手机用户数据集中,样本数量分布存在严重的非平衡性,非换机样本数是换机样本数的几十倍,是一个典型的不平衡数据集.本文针对运营商用户的某一个月产生的数据情况,应用本文方法进行处理,得到决策规则并对另一个月的用户数据进行匹配,从而进行换机意向预测.实验设计如下:
学习集为某电信运营商4月20万按自然比例(非换机∶换机=27∶1)分布的数据记录,测试集为5月40万按1∶1分布的数据记录.通过特征选取和专家经验相结合,选择了19个属性作为预测模型的输入特征,此外,鉴于在学习过程中各属性之间相互独立,但在实际情况中用户近3个月的贡献收入、通话时间及流量联系紧密,所以人为添加了9个属性来衡量3个月间属性的变化情况,具体描述如表6所示:

Table 6 Description of User Data Attribute

Continued (Table 6)
首先对连续属性按照专家经验知识进行离散化处理,并利用粗糙集作属性约简,得到最终用于学习的25个属性: jiling,old_online_month,AGE,countimei,avg_hjzhouqi,tac_month,arpu1,arpu2,mou1,mou2,mou3,dou1,dept,new_flag,price_flag,arpu12,arpu23,mou12,mou23,dou12,dou23,arpu,mou,dou,class,然后采用KAcBag算法进行学习,并与EBBag算法(随机欠抽样+bagging技术)进行对比,实验结果如表7所示,黑体表示评价指标在2种算法上的最大值.

Table 7 Experimental Results
由表7可以看出,本文的抽样方法较随机欠抽样方法在2项指标上有明显的提高,能有效识别出换机用户,并降低非换机用户的误分率,特别对具有大量样本的数据集来说,1个百分点的提高会带来非常可观的收益,说明基样本权重的欠抽样方法在预测用户换机等追求正确率的工程问题下应用前景广阔.
4 结束语
在实际应用领域中存在着大量的不平衡数据集,然而传统的机器学习算法对少数类的识别率较低.本文提出一种基于样本权重的不平衡数据欠抽样方法,该方法通过样本权重来刻画多数类样本所处的区域,在多次聚类后确定各样本的权重;然后根据权重大小抽取对多数类样本进行欠抽样处理,使位于中心区域的多数类样本较容易被抽中,与所有少数类样本组成平衡的训练集,提高少数类的识别率,并融合集成学习的思想,通过分类器加权投票提高数据集整体的分类性能.在UCI数据集和移动用户换机数据上的实验表明,本文提出的抽样方法充分利用了少数类和多数类的分布信息,抽样所得样本较好地保持了多数类信息,同时有效缩小了数据集规模,提高了分类器的分类性能.
在调用 KAcBag方法时,为了选取能够取得最佳预测性能的分类器,需要设置恰当的聚类次数、类簇的个数以及簇减少的步长,本文主要是通过大量的实验来得到最优结果,关于如何根据训练集的样本数及类分布特点自适应地确定参数,是后续研究的重点.
[1]Xiao J, Xie L, He C, et al. Dynamic classifier ensemble model for customer classification with imbalanced class distribution[J]. Expert Systems with Applications, 2012, 39(3): 3668-3675
[2]Yu H, Ni J, Zhao J. ACOSampling: An ant colony optimization-based undersampling method for classifying imbalanced DNA microarray data[J]. Neurocomputing, 2013, 101: 309-318
[3]Wang S, Yao X. Using class imbalance learning for software defect prediction[J]. IEEE Trans on Reliability, 2013, 62(2): 434-443
[4]Ma Z, Yan R, Yuan D, et al. An imbalanced spam mail filtering method[J]. International Journal of Multimedia and Ubiquitous Engineering, 2015, 10(3): 119-126
[5]Kim H, Howland P, Park H. Dimension reduction in text classification with support vector machines[J]. Journal of Machine Learning Research, 2005, 6(1): 37-53
[6]Maes F, Vandermeulen D, Suetens P. Medical image registration using mutual information[J]. Proceedings of the IEEE, 2003, 91(10): 1699-1722
[7]Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: Synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357
[8]Han H, Wang W Y, Mao B H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning[C] //Proc of the Int Conf on Intelligent Computing. Berlin: Springer, 2005: 878-887
[9]Kubat M, Matwin S. Addressing the curse of imbalanced training sets: One-sided selection[C] //Proc of the 14th Int Conf on Machine Learning. San Francisco, CA: Morgan Kaufmann, 1997: 179-186
[10]Yen S J, Lee Y S. Cluster based under-sampling approaches for imbalanced data distributions[J]. Expert Systems with Applications, 2009, 36(3): 5718-5727
[11]Zhang S. Decision tree classifiers sensitive to heterogeneous costs[J]. Journal of Systems and Software, 2012, 85(4): 771-779
[12]Park Y, Luo L, Parhi K K, et al. Seizure prediction with spectral power of EEG using cost-sensitive support vector machines[J]. Epilepsia, 2011, 52(10): 1761-1770
[13]Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 23-140
[14]Freund Y, Schapire R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139
[15]Fan W, Stolfo S J, Zhang J, et al. AdaCost: Misclassification cost-sensitive boosting[C] //Proc of the 16th Int Conf on Machine Learning. San Francisco, CA: Morgan Kaufmann, 1999: 97-105
[16]Hido S, Kashima H, Takahashi Y. Roughly balanced bagging for imbalanced data[J]. Statistical Analysis and Data Mining, 2009, 2(5/6): 412-426
[17]Blaszczynski J, Stefanowski J. Neighbourhood sampling in bagging for imbalanced data[J]. Neurocomputing, 2015, 150: 529-542
[18]Wang S, Yao X. Diversity analysis on imbalanced data sets by using ensemble models[C] //Proc of IEEE Symp on Computational Intelligence and Data Mining. Piscataway, NJ: IEEE, 2009: 324-331
[19]MacQueen J. Some methods for classification and analysis of multivariate observations[C] //Proc of the 15th Berkeley Symp on Mathematical Statistics and Probability. Berkeley, CA: University of California Press, 1967: 281-297
[20]Su C T, Chen L S, Yih Y. Knowledge acquisition through information granulation for imbalanced data[J]. Expert Systems with Applications, 2006, 31(3): 531-541
[21]Chen Si, Guo Gongde, Chen Lifei. Clustering ensembles based classification method for imbalanced data sets[J]. Pattern Recognition and Artificial Intelligence, 2010, 23(6): 772-780 (in Chinese)
(陈思, 郭躬德, 陈黎飞. 基于聚类融合的不平衡数据分类方法[J]. 模式识别与人工智能, 2010, 23(6): 772-780)
[22]Japkowicz N, Shah M. Evaluating Learning Algorithms: A Classification Perspective[M]. Cambridge, UK: Cambridge University Press, 2011
[23]Witten I H, Frank E. Data Mining: Practical Machine Learning Tools and Techniques[M]. San Francisco, CA: Morgan Kaufmann, 2005

Xiong Bingyan, born in 1991. Master. Her main research interests include data mining and rough set.

Wang Guoyin, born in 1970. Professor and PhD supervisor. Member of China Computer Federation. His main research interests include rough set, neural network, machine learning and data mining (wanggy@cqupt.edu.cn).

Deng Weibin, born in 1978. PhD and associate professor. His main research interests include intelligent information processing and uncertainty decision (dengwb@cqupt.edu.cn).
Under-Sampling Method Based on Sample Weight for Imbalanced Data
Xiong Bingyan, Wang Guoyin, and Deng Weibin
(ChongqingKeyLaboratoryofComputationalIntelligence,ChongqingUniversityofPostsandTelecommunications,Chongqing400065)
Imbalanced data exists widely in the real world, and its classification is a hot topic in data mining and machine learning. Under-sampling is a widely used method in dealing imbalanced data set and its main idea is choosing a subset of majority class to make the data set balanced. However, some useful majority class information may be lost. In order to solve the problem, an under-sampling method based on sample weight for imbalance problem is proposed, named as KAcBag (K-means AdaCost bagging). In this method, sample weight is introduced to reveal the area where the sample is located. Firstly, according to the sample scale, a weight is made for each sample and is modified after clustering the data set. The samples which have less weight in the center of majority class. Then some samples are drawn from majority class in accordance with the sample weight. In the procedure, the samples in the center of majority class can be selected easily. The sampled majority class samples and all the minority class samples are combined as the training data set for a component classifier. After that, we can get several decision tree sub-classifiers. Finally, the prediction model is constructed based on the accuracy of each sub-classifiers. Experimental tests on nineteen UCI data sets and telecom user data show that KAcBag can make the selected samples have more representativeness. Based on that, this method can improve the the classification performance of minority class and reduce the scale of the problem.
imbalanced data; under-sampling; sample weight; clustering; ensemble learning
2015-06-19;
2015-10-29
国家自然科学基金项目(61272060);教育部人文社科规划基金项目(15XJA630003);重庆市教委科学技术研究项目(KJ1500416);重庆市自然科学基金项目(CSTC2013jjB40003)
王国胤(wanggy@cqupt.edu.cn)
TP391
This work was supported by the National Natural Science Foundation of China (61272060), the Social Science Foundation of the Chinese Education Commission (15XJA630003), the Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJ1500416), and the Key Natural Science Foundation of Chongqing (CSTC2013jjB40003).

