信息表中概念漂移与不确定性分析

邓大勇苗夺谦黄厚宽

1(浙江师范大学数理与信息工程学院 浙江金华 321004)2(同济大学电子与信息工程学院 上海 201804)3(北京交通大学计算机与信息技术学院 北京 100044)4(浙江师范大学行知学院 浙江金华 321004)(dayongd@163.com)



信息表中概念漂移与不确定性分析

邓大勇1,2,4苗夺谦2黄厚宽3

1(浙江师范大学数理与信息工程学院 浙江金华 321004)2(同济大学电子与信息工程学院 上海 201804)3(北京交通大学计算机与信息技术学院 北京 100044)4(浙江师范大学行知学院 浙江金华 321004)(dayongd@163.com)

概念漂移探测是数据流挖掘的一个研究重点，不确定性分析是粗糙集理论的研究核心之一. 结合数据流、概念漂移和粗糙集、F-粗糙集的基本观点，以上下近似为工具，定义了上下近似概念漂移、上下近似概念耦合等概念，据此分析了信息表内概念随着属性而变化的特点. 以正区域为工具，定义了决策表内概念漂移、概念耦合等概念，分析了决策表内整体概念随属性变化而变化. 在认识论方面,从理想和现实2方面定义了认识收敛， 从粒计算、粗糙集的角度对人类认识世界的方式进行了探讨.

粗糙集；概念漂移；属性约简；概念耦合；上下近似

现实中的数据往往随着时间的变化而变化，例如证劵交易数据、微博、视频、传感器数据等，这种类型的数据称为数据流[1].数据流具有按照时间顺序排列、快速变化、海量甚至无限并且可能出现概念漂移现象等特征[2-3].数据流挖掘是当前数据挖掘研究的一个热点，数据流分类和概念漂移探测是数据流挖掘的主要研究方向.

粒计算[4-5]是人类智能处理问题的思维方式，也是处理不确定性问题的方法.粒计算的主要方法有模糊集[6]、粗糙集[7-9]、商空间[10]和云模型[11]等. 粗糙集理论[7-9]是一种处理不精确、不完全、含糊数据的有效数学工具，是数据挖掘和分类的重要方法.传统的粗糙集理论不太适合研究海量的、动态变化的数据，也不太适合研究数据流；F-粗糙集[12-13]将粗糙集理论从单个信息表或决策表推广到多个，比较适合研究动态变化的数据，能够研究数据流和概念漂移.

利用粗糙集理论研究数据流和概念漂移比较少见.文献[14-15]利用粗糙集的上下近似的变化去度量概念漂移；文献[16]把每个滑动窗口看成是一个决策子表，利用并行约简的方法整体删除冗余属性，通过比较不同子表之间的属性重要性变化探测概念漂移.

粗糙集一个非常大的优势在于不确定性分析.研究者们提出了上下近似[7-9]、隶属度[17]、信息熵[18]、条件熵[19-20]、粗糙熵、模糊熵[21-22]等不确定性度量指标来刻画和描述数据的不确定性.其中最原始、最本质、最核心的不确定性分析和度量指标是上下近似.

本文结合数据流、概念漂移和粗糙集、F-粗糙集的基本观点、基本方法，分析了信息表内信息粒度的概念变化和整个信息表内概念的整体变化.首先利用上下近似分析了信息表内单个概念的变化，定义了上下近似概念漂移与概念耦合等指标，在信息粒度变化的基础上度量概念随着属性而变化的特点;其次，在整个信息表内，用正区域的变化度量整个信息表或决策表内整体概念随属性而变化的特性；最后，分别定义了决策表内和信息表内认识收敛的概念,分析了概念漂移、概念耦合等指标的认识论意义.

1 基础知识

本节简单介绍粗糙集[7-9]的相关基本知识.

IS=(U,A)是一个信息系统，其中U是论域，A是论域U上的条件属性集.对于每个属性a∈A都对应着一个函数a:U→Va，Va称为属性a的值域，U中每个元素称为个体、对象或行.

对于每一个属性子集B⊆A和任何个体x∈U都对应着一个信息函数：

InfB(x)={(a,a(x)):a∈B}.

B-不分明关系(或称为不可区分关系)定义为

IND(B)={(x,y):InfB(x)=InfB(y)}.

任何满足关系IND(B)的2个元素x，y都不能由属性子集B区分，[x]B表示由x引导的IND(B)等价类.

对于信息系统IS=(U,A)、属性子集B⊆A和论域子集X⊆U，上下近似与边界线的个体表示为

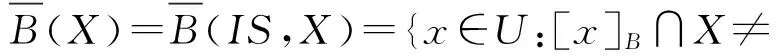
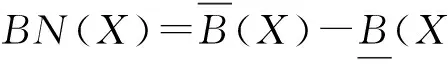
上下近似及边界线的信息粒度表示为

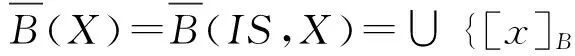
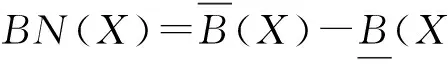
在决策系统DS=(U,A,d)中，{d}∩A=∅，决策属性d将论域U划分为块，U/{d}={Y1,Y2,…,Yp}，其中Yi(i=1,2,…,p)是等价类.决策系统DS=(U,A,d)的正区域定义为

有时决策系统DS=(U,A,d)的正区域POSA(d)也记为POSA(DS,d)或POS(DS,A,d).

定义1[7-9]. 在决策系统DS=(U,A,d)中，B⊆A是DS的约简iffB⊆A满足2个条件：

1)POSB(d)=POSA(d)；

2) 对于任意S⊂B,有POSS(d)≠POSB(d).

定义2[23]. 在决策系统DS=(U,A,d)中,U/{d}={Y1,Y2,…,Yp}，对于任意a∈A，有U/{a}={[x1]{a},[x2]{a},…,[xn]{a}}，则B⊆A是Y∈U/{d}的值约简iffB⊆A满足2个条件：

2 信息粒度的概念漂移与不确定性分析

一个概念，它既可能用外延表示，也可能用内涵表示.但概念不一定是精确的，所以粗糙集常用上下近似来表示和逼近一个概念.本节我们将研究概念的上下近似在同一个信息表中的变化，即概念漂移与概念耦合.

推论1. 在一个信息表IS=(U,A)中，对于∅⊂B1⊆B2⊆A和X⊆U，有BNB2(X)⊆BNB1(X).

我们将文献[15]中的度量概念漂移、概念耦合等指标进行改进，使之能更好地度量信息系统中概念的变化.

定义3. 设信息表IS=(U,A)中， ∅⊂B1⊆B2⊆A和X⊆U，则概念X相对于B1，B2的上下近似漂移定义为

定义4. 设信息表IS=(U,A)中， ∅⊂B1⊆B2⊆A和X⊆U，则概念X相对于B1，B2的上下近似耦合度定义为

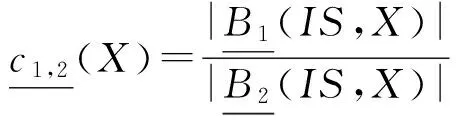
其中,|·|表示“·”的势.

概念X相对于B1，B2的上下近似漂移度定义为

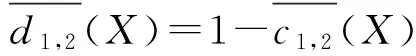
定理2. 设DS=(U,A,d)是一个决策系统，B1⊆A是一个约简，则对于任意的B1⊆B2⊆A和任意概念X={x|d(x)=d1∧x∈U}(其中d1为常数)，有：

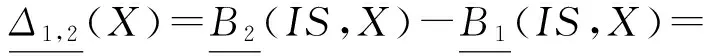
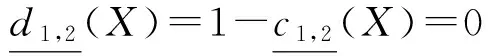
证明. 我们只证明第1个公式，后面2个公式由第1个公式立即推得.

证毕.

定理3. 设DS=(U,A,d)是一个决策系统，B1⊆A是一个约简，则对于任意的B0⊂B1⊆A,则存在概念X={x|d(x)=d1∧x∈U}使得：

证明. 与定理2的证明方式类似，我们只证明第1个公式，后面2个公式由第1个公式立即推得.

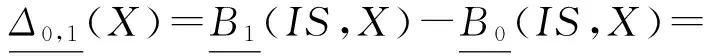
证毕.

定理4. 设DS=(U,A,d)是一个决策系统，X={x|d(x)=d1∧x∈U}是一个概念，B1⊆A是X的一个值约简，则：

证明. 根据值约简的定义以及相应的概念漂移、概念耦合等定义，立得上述结论.

证毕.

例1. 设DS1=(U,A,d)是决策表，如表1所示.其中，a,b,c是条件属性，d是决策属性.

Table 1 A Decision System DS1

令X={x|d(x)=0,x∈U},B0={a},B1={a,b},则：

{y1,y4}-{y1,y4}=∅；

{y1,y2,y3,y4,y5,y6}-{y1,y4,y5,y6}={y2,y3}；

容易看出，B0是决策表DS1的约简,定理1,2,3,4都成立.

3 决策表整体的概念漂移与不确定性分析

第2节讨论是针对信息表或决策表内单个概念的概念漂移与耦合，对于整个决策表或信息表这些指标显得非常局限，因为一个决策表或信息表中有多个概念，将多个概念放在一起讨论概念漂移、耦合及其度量是本节讨论的内容.

定理5[24]. 设DS=(U,A,d)是一个决策系统,∅⊂B1⊆B2⊆A,则有POSB1(d)⊆POSB2(d)⊆POSA(d).

根据定理5将文献[15]中的指标进行改造,我们得到下面概念漂移、概念耦合的度量指标.

定义5. 设DS=(U,A,d)是一个决策系统,∅⊂B1⊆B2⊆A,则决策表中相对于B1，B2的概念漂移定义为

Δ1,2=POSB2(d)-POSB1(d).

定义6. 设DS=(U,A,d)是一个决策系统,∅⊂B1⊆B2⊆A,则决策表中相对于B1，B2的概念耦合度定义为

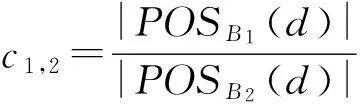
定义7. 设DS=(U,A,d)是一个决策系统,∅⊂B1⊆B2⊆A,则决策表中相对于B1，B2的概念漂移度定义为

定理6. 设DS=(U,A,d)是一个决策系统，B1⊆A是一个约简，则对于任意的B1⊆B2⊆A，有：

Δ1,2=POSB2(d)-POSB1(d)=∅，

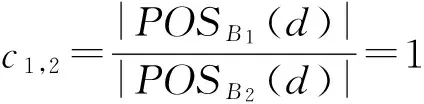
证明. 根据定理5、定义5～7及属性约简的定义，立得上述结论.

证毕.

定理7. 设DS=(U,A,d)是一个决策系统，B1⊆A是一个约简，则对于任意的B0⊂B1⊆A,

Δ0,1=POSB1(d)-POSB0(d)≠∅,

证明. 根据定理5、定义5～7及属性约简的定义，立得上述结论.

证毕.

例2. 设DS2=(U,A,d)是决策表，如表2所示.其中，a，b，c是条件属性，d是决策属性.

Table 2 A Decision System DS2

令B1={a},B2={a,b}，则：

POSB1(d)={x2,x4}；

POSB2(d)={x1,x2,x3,x4}；

Δ1,2=POSB2(d)-POSB1(d)={x1,x3}；

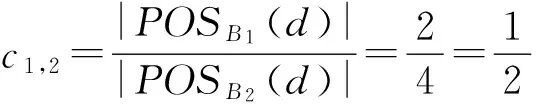
在决策表DS2中，B2是它的一个约简，容易看出，定理5～7都成立.

4 概念漂移与不确定性分析的认识论意义

粗糙集理论认为“知识就是分类”,区分不同的物体是人类知识的体现,在此过程中也需要知识,也就是说知识需要知识来表达. 但不同的知识表达不一样,人类的认识是一个过程,在这个认识过程中选取什么特征来表达知识?选取多少特征?到什么时候为止?这些问题对于人类来说目前都是一个自发的直觉过程,缺乏理性思考. 继承文献[25]的思想，下面我们利用粗糙集和概念耦合的思想来努力回答这些问题.

在决策系统DS=(U,A,d)中,假定条件属性集A1⊂A2⊂…⊂An⊂…=A是一个不断变化的过程,也是一个认识不断深入的过程，我们通过A来表达和认识d.

认识收敛有2条标准：

1)POSA(d)=U；

这2条标准也是认识收敛的定义. 标准1表明决策系统DS=(U,A,d)是一致的，所有概念的边界区域为空，它们的上近似等于下近似；标准2表明增加的属性An-An-1对于区分表中的个体不起作用. 标准1是理想的标准,标准2是现实的标准,这是因为现实世界中并不是每个概念都是精确的,很多概念都是含糊不清、边界线不为空的.

在信息系统IS=(U,A)中，因为没有决策属性d的约束,认识收敛的标准定义如下：

3) 对于任意的概念X⊆U,有：

且

标准3表明从An-1到An对于信息系统IS=(U,A)中的每一个概念都不会发生变化.

标准1是一个理想的标准,在这个标准中所有的对象都被清晰地区分，没有不确定、没有模糊、也没有粗糙；标准2和标准3只是一个局部收敛的标准，随着认识的进一步深入，比如从An到An+1这些指标值也许不等于1，这时认识达到了一个新的高度. 例如:长期以来人们识别某个人,一般是根据相貌、体态、步态、声音等，这种识别方式虽然有一定的误差，但基本稳定. 只有到了近年来,使用DNA技术才能彻底区分不同的人.

当然,我们可以等价地用概念漂移度来定义和度量认识收敛,这里不再赘述.

5 结论与展望

从粒计算、粗糙集和数据流、概念漂移的角度观察信息表，以上下近似为工具，本文定义了概念的上下近似漂移、上下近似耦合等概念，分析了信息表内概念随属性的变化而变化的特性.从单个概念和整个信息表或决策表2种不同的粒度层次上分析和度量了概念漂移和概念耦合.从信息表和决策表的角度定义了认识收敛的概念,指出其认识论意义.

进一步的研究有：运用更多的粒计算、粗糙集不确定性分析方法和指标，分析和度量数据流或信息表中隐藏的不确定性，并将结果应用于集成分类器和数据流分类.

[1]Babcock B, Babu S, Dater M, et al. Models and issues in data stream systems[C] //Proc of the 21st ACM SIGACT-SIGMOD-SIGART Symp on Principles Database Systems. New York: ACM, 2002: 1-30

[2]Wang Tao, Li Zhoujun, Yan Yuejin, et al. A survey of classification of data streams[J]. Journal of Computer Research and Development, 2007, 44(11): 1809-1815 (in Chinese)

(王涛, 李舟军, 颜跃进, 等. 数据流挖掘分类技术综述[J]. 计算机研究与发展, 2007, 44(11): 1809-1815)

[3]Xu Wenhua, Qin Zheng, Chang Yang. Semi-supervised learning based ensemble classifier for stream data[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(2): 292-299 (in Chinese)

(徐文华, 覃征, 常扬. 基于半监督学习的数据流集成分类算法[J]. 模式识别与人工智能, 2012, 25(2): 292-299)

[4]Hobbs J R. Granularity[C] //Proc of the 9th Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 1985: 432-435

[5]Lin T Y. Granular Computing[M]. Announcement of the BASIC Special Interest Group on Granular Computing, 1997[6]Zadel L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338-353

[7]Pawlak Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356

[8]Pawlak Z. Rough Sets—Theoretical Aspect of Reasoning about Data[M]. Dordrecht, the Netherland: Kluwer Academic Publishers, 1991

[9]Wang Guoyin. Rough Set Theory and Knowledge Acquisition[M]. Xi’an: Xi’an Jiaotong University Press, 2001 (in Chinese)

(王国胤. Rough集理论与知识获取[M]. 西安: 西安交通大学出版社, 2001)

[10]Zhang Bo, Zhang Ling. Theories and Applications for Problem Solving[M]. Beijing: Tsinghua University Press, 1990 (in Chinese)

(张钹, 张铃. 问题求解理论及应用[M].北京: 清华大学出版社,1990)

[11]Li Deyi, Meng Haijun, Shi Xuemei. Membership clouds and membership cloud generators[J]. Journal of Computer Research and Development, 1995, 32(6): 16-18 (in Chinese)

(李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995, 32(6): 16-18)

[12]Deng Dayong, Chen Lin. Parallel Reducts and F-rough Sets[M] //Cloud Model and Granular Computing. Beijing: Science Press, 2012: 210-228 (in Chinese)

(邓大勇, 陈林. 并行约简与F-粗糙集[M] //云模型与粒计算. 北京：科学出版社, 2012: 210-228)

[13]Chen Lin. Parallel reducts and decision in various levels of granularity[D]. Jinhua, Zhejiang: Zhejiang Normal University, 2013 (in Chinese)

(陈林. 粗糙集中不同粒度层次下的并行约简及决策[D]. 浙江金华: 浙江师范大学, 2013)

[14]Cao Fuyuan, Huang Joshua Zhexue. A concept-drfting detection algorithm for categorical evolving data[G] //LNAI 7819: Proc of the 17th Pacific-Asia Conf on Knowledge Discovery and Data Mining. Berlin: Springer, 2013: 485-496

[15]Deng Dayong, Pei Minghua, Huang Houkuan. The F-rough sets approaches to the measures of concept drift[J]. Journal of Zhejiang Normal University: Natural Sciences, 2013, 36(3): 303-308 (in Chinese)

(邓大勇, 裴明华, 黄厚宽. F-粗糙集方法对概念漂移的度量[J]. 浙江师范大学学报: 自然科学版, 2013, 36(3): 303-308)

[16]Deng Dayong, Xu Xiaoyu, Huang Houkuan. Concept drifting detection for categorical evolving data based on parallel reducts[J]. Journal of Computer Research and Development, 2015, 52(5): 1071-1079 (in Chinese)

(邓大勇, 徐小玉, 黄厚宽. 基于并行约简的概念漂移探测[J]. 计算机研究与发展, 2015, 52(5): 1071-1079)

[17]Pawlak Z, Skowron A. Rough membership functions[C] //Adances in the Dempster Shafer Theory of Evidence. New York: John Wiley, 1994: 251-271

[18]Miao Duoqian, Hu Guirong. A heuristic algorithm for reduction of knowledge[J]. Journal of Computer Research and Development, 1999, 36(6): 681-684 (in Chinese)

(苗夺谦, 胡桂荣. 知识约简的一种启发式算法[J]. 计算机研究与发展, 1999, 36(6): 681-684)

[19]Wang Guoyin, Yu Hong, Yang Dachun. Decision table reduction on conditional information entropy[J]. Chinese Journal of Computers, 2002, 25(7): 759-766 (in Chinese)

(王国胤, 于洪, 杨大春. 基于条件信息熵的决策表约简[J]. 计算机学报, 2002, 25(7): 759-766)

[20]Yang Ming. Approximate reduction based on conditional information entropy in decision tables[J]. Acta Eletronica Sinica, 2007, 35(11): 2156-2160 (in Chinese)

(杨明. 决策表中基于条件信息熵的近似约简[J]. 电子学报, 2007, 35(11): 2156-2160)

[21]Liang J Y, Chin K S, Dang C Y. A new method for measuring uncertainty and fuzziness in rough set theory[J]. International Journal of General Systems, 2002, 31(4): 331-342

[22]Liang Jiye, Li Deyu. Uncertainty and Knowledge Acquisition in Information Systems[M]. Beijing: Science Press, 2005 (in Chinese)

(梁吉业, 李德玉. 信息系统中的不确定性与知识获取[M]. 北京: 科学出版社, 2005)

[23]Lin Jiayi, Peng Hong, Zheng Qilun. A new algorithm for value reduction based on rough set[J]. Computer Engineering, 2003, 29(4): 70-71 (in Chinese)

(林嘉宜, 彭宏, 郑启伦. 一种新的基于粗糙集的值约简算法[J]. 计算机工程, 2003, 29(4): 70-71)

[24]Qian Y H, Liang J Y, Pedrycz W, et al. Positive approximation: An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence, 2010, 174: 597-618

[25]Deng Dayong, Jiang Feng, Liu Qing. Data reduction & machine learning based on rough set approach[J]. Computer and Modernization, 2002 (1): 21-23 (in Chinese)

(邓大勇, 江峰, 刘清. 基于Rough 集方法的数据约简与机器学习[J]. 计算机与现代化, 2002 (1): 21-23)

Deng Dayong, born in 1968. PhD and associate professor. His main research interests include rough sets, granular computing and data mining.

Miao Duoqian, born in 1964. PhD. Professor and PhD supervisor. His main research interests include rough sets, granular computing, data mining, comput-ational intelligence and image processing.

Huang Houkuan, born in 1940. Professor and PhD supervisor. His main research interests include computational intelligence, data mining and multi-agent system.

Analysis of Concept Drifting and Uncertainty in an Information Table

Deng Dayong1,2,4, Miao Duoqian2, and Huang Houkuan3

1(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua,Zhejiang321004)2(SchoolofElectronicsandInformation,TongjiUniversity,Shanghai201804)3(SchoolofComputerandInformationTechnology,BeijingJiaotongUniversity,Beijing100044)4(XingzhiCollege,ZhejiangNormalUniversity,Jinhua,Zhejiang321004)

Concept drifting detection is one of hot topics in data stream mining, and analysis of uncertainty is dominant in rough set theory. Combined with the ideas of data stream, concept drifting, rough sets and F-rough sets, a lot of concepts such as concept drifting of upper approximation, concept drifting of lower approximation, concept coupling of upper approximation and concept coupling of lower approximation etc are defined. The change of concepts in an information system is analyzed with these definitions. With the positive region, integral concept drifting, integral concept coupling are defined. The analysis and measurement for the change of concept uncertainty are conducted. From the view of epistemology, the concept of cognition convergence is defined from the ways of idealism and realism. It provides heuristic information for realizing the world of human beings from the viewpoints of granular computing and rough sets.

rough sets; concept drift; attribute reduction; concept coupling; upper and lower approximation

2015-09-06；

2016-02-05

国家自然科学基金项目(61473030,61572442,61203247,61273304,61573259,61472166);浙江省自然科学基金项目(LY15F020012,LY13F020016)

TP18

This work was supported by the National Natural Science Foundation of China (61473030,61572442,61203247,61273304,61573259,61472166) and the Natural Science Foundation of Zhejiang Province of China (LY15F020012,LY13F020016).