基于RLWE的身份基认证密钥交换协议
赵秀凤 高海英 王爱兰
(解放军信息工程大学 郑州 450001)(zhao_xiu_feng@163.com)
基于RLWE的身份基认证密钥交换协议
赵秀凤 高海英 王爱兰
(解放军信息工程大学 郑州 450001)(zhao_xiu_feng@163.com)
提出了一个基于分圆环上错误学习(learning with errors, LWE)问题的身份基认证密钥交换协议,其基本思想是利用环上错误学习(ring learning with errors, RLWE)采样生成系统主私钥,进一步生成用户私钥,通过交换Diffie-Hellman临时公钥,计算用于派生会话密钥的密钥材料. 该协议与传统密钥交换协议的区别在于,协议中引入了错误项,以理想格的解码基为工具,详细分析协议的容错性,给出了合理的参数设置建议,从而保证协议以显著概率计算出相同的会话密钥. 协议在ID-BJM模型下具有可证明AKE安全性和PKG安全性,并且在双方临时私钥泄露、双方长期私钥泄露以及A的长期私钥和B的临时私钥泄露这3种情况下也可以保证协议的AKE安全.
分圆环;环LWE;可证明安全;基于身份的密码;密钥交换协议
密钥交换协议使得通信系统中的参与方通过在公开的信道上交换信息计算一个共同的会话密钥,用于以后的保密通信或消息认证.比如Internet密钥交换协议为IPSec安全协议的用户提供安全的会话密钥.
1976年,Diffie和Hellman[1]基于离散对数问题的困难性给出了第1个密钥交换协议,这一研究成果开创了公钥密码学研究领域.1984年,Shamir[2]提出了“基于身份密码学”的概念,大大降低了证书管理的负担.随后,基于身份的密钥交换协议相继提出,这些协议绝大部分是基于双线性对构造的[3-5].由于双线性对运算的复杂性比较高,因此设计不使用双线性对的基于身份的密钥交换协议更为实用.
格上困难问题(如最近向量问题、最短向量问题)具有抗量子计算攻击的特性,并且格上的运算是矩阵-向量的乘法,具有较低的计算复杂性,因此基于格的密码学成为研究热点,并构造了全同态加密、属性加密等新型加密体制.由于基于最小整数解(small integer solution, SIS)问题的单向函数不具备交换性,因此,直接构造基于格的Diffie-Hellman形式的密钥交换协议成为公开问题.直到2012年,Ding等人[6]首次给出了带有噪声的基于理想格的密钥交换协议,使得通信双方以显著概率协商一个会话密钥.基于Ding等人的协议,Zhang等人[7]给出了HMQV形式的基于格的认证密钥交换协议.2014年,Peikert[8]利用分圆环上的调和函数构造了密钥封装机制,有效实现了密钥交换.文献[9-10]对基于环错误学习(ring learning with errors, RLWE)的认证密钥交换协议进行了实用化研究.
1 基础知识
1.1 亚高斯随机变量
对于任意的δ>0,称上的随机变量X服从参数为r>0的δ-亚高斯分布,如果对于所有的t∈,生成函数满足:

对于所有的t≥0,X满足高斯不等式:
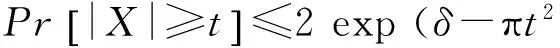
(1)
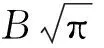
同样,可以定义向量的亚高斯分布.称一个随机实数向量Y服从参数为r的δ-亚高斯分布,如果对于所有的单位向量u,随机变量u,Y∈服从参数为r的δ-亚高斯分布.

1.2 分圆环
对于整数n,令K=(ξm)表示m次分圆域,R=[ξm]⊂K表示m次分圆环,其中ξm表示一个阶为m的抽象元素.ξm在有理数域上的极小多项式称为分圆多项式φm(X)∈[X],其复数根为本原m次单位根,其中/m)∈.因此,环R可看作的扩张,度为n=φ(m),并且同构于商环[X]/(φm(X)).特别地,为环R的一组基,称为幂基(power basis).
对于任意的整数模q≥1,令Rq表示商环R/qR.
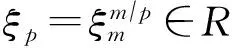



1.3 解码基

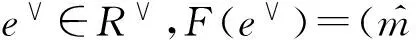

即e∨与e的系数向量相同.因此,分式理想R∨中对错误e∨采样的算法同时适用于在理想R中对错误e进行采样,前提条件是e∨与e都用各自的解码基表示.



在本文中,我们假设g×e服从亚高斯分布,并对错误项e关于R解码基的系数进行具体分析.

1.4 错误分布
对于r>0,上参数为r的高斯分布Dr的概率分布函数为exp(-πx2/r2)/r.本文定义数域K上的错误分布/g)×Dr,通过在分布ψ上采样得到a∈K,然后对a的每个系数最近取整,从而将ψ离散化到环R上,记为χ.


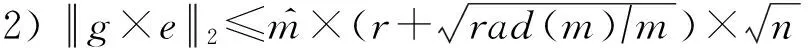
1.5 RLWE问题

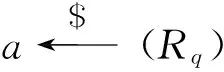

下面以定理的形式给出结论:判定性RLWE问题是困难的.

1.6 近似函数和调和函数


文献[8]利用上述交叉近似函数定义了调和机制.如果q为奇数,为了避免派生位流的不均匀性,引入了随机化函数.令dbl:q→2q,dbl(x)=2x-e.其中e为随机项,e以1/2的概率设置为0,1/4的概率设置为1和-1,从而保证e在模2运算后是均匀的.下面的引理说明对于随机选择的元素v∈q,已知dbl(v)q,2的情况下,q,2在2q中是均匀随机的.
引理5[8]. 对于奇数q, 如果v∈q是均匀随机的,令2q,那么给定q,2在2q上是均匀随机的.
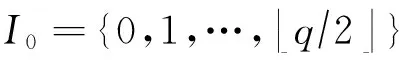
下面的引理表明对于随机元素v∈q,已知与v近似的w和交叉近似函数dbl(v)q,2,可以恢复q,2.
引理6[8]. 对于奇数q, 令v=w+e∈q,w,e∈q使得2e∓1∈Emodq,那么rec(2w,dbl(v)q,2)=q,2.
上述近似函数的定义和调和机制可以利用解码基扩展到分圆环[8].
2 ID-BJM模型简介
2002年,Chen等人[3]将Ballare-Roaryway模型扩展到基于身份密钥交换协议的背景下,称为ID-BJM模型,本节我们简要回顾ID-BJM模型.

ID-BJM模型中会话密钥的安全性通过挑战者和攻击者之间的游戏定义.首先攻击者A选择一定数量的诚实参与者,在游戏的第1阶段,攻击者可以自适应地进行如下查询:
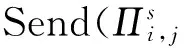

3) Corrupt(i) 返回参与者i的长期私钥,称参与者i被腐化.
在Test查询之后,A可以继续进行查询预言机,但是不允许对测试会话及其匹配会话进行Reveal查询,也不允许对测试会话参与者的伙伴进行Corrupt查询,直到输出b′∈{0,1}作为对b的判断.若b′=b,且Test查询的测试会话是新鲜的,则称敌手A赢得了此游戏.
定义4. AKE安全.在ID-BJM模型下,敌手A攻击协议的优势为
AdvA=|2Pr[b′=b]-1|.
对于任意的概率多项式时间敌手A,如果A赢得上述游戏的优势AdvA是可忽略的,则称该基于身份的认证密钥协商协议是安全的.

3 RLWE-IDAKE协议
3.1 符号表示
1) 正整数m表示第m个分圆环R,阶为n=φ(m).
2) 正整数q为模数,与整除m的任意一个奇素数互素,从而使得g∈R与q互素.为了保证协议的效率和安全性,这里选取的q为素数且满足qmodm=1.

4) 随机化函数dbl:q→2q.
5) 调和函数rec:2q×2→2.
3.2 协议描述
基于身份密钥交换协议包括3个算法:系统建立Setup、密钥抽取算法Extract和密钥交换过程Keyexchange.
3.2.1 系统建立Setup
密钥生成中心PKG执行如下步骤:
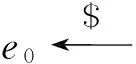
系统公开参数为MPK={M,M1,H1,H},系统主密钥为MSK={S}.
3.2.2 密钥抽取算法Extract(IDi,MSK)
1) 对每个用户IDi,PKG计算Ii=H1(IDi),其中Ii是环Rq中的小范数元素.
2) PKG计算Si=IiS+Mei,其中ei←χ,用户IDi的私钥为Si.
3.2.3 密钥交换Keyexchange
假设用户IDA和用户IDB试图通过交换公开信息计算共享的会话密钥,他们的私钥分别为SA和SB,令bA=IAM1,cA=IAM-1,bB=IBM1,cB=IBM-1.
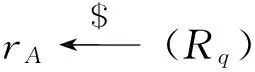
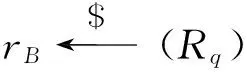
vB1=guArB+gB1∈Rq,
vB2=gbArB+gB2∈Rq,
vB3=gcASB+gB3∈Rq,

3) 用户IDA计算:
vA1=guBrA∈Rq,
vA2=guBSA∈Rq,
vA3=gcBSA∈Rq,
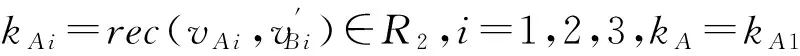
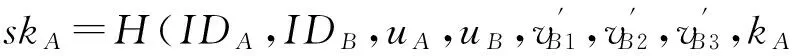
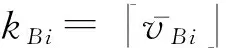

3.3 正确性分析
如果用户IDA和用户IDB诚实地运行协议,那么他们将以显著概率计算一个共享的会话密钥.
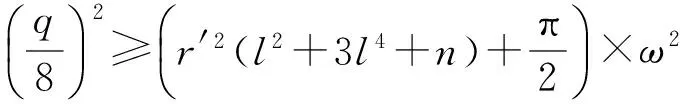
其中,r′2=r2+2π×rad(m)/m,那么基于身份的密钥交换协议RLWE-IDAKE可以显著概率计算出相同的会话密钥,即skA=skB,其错误概率为n的可忽略函数.
证明. 由引理7~9可直接得出:
kA1=kB1,kA2=kB2,kA3=kB3,
从而有:
kA=kA1⊕kA2⊕kA3=kB1⊕kB2⊕kB3=kB.

证毕.

其中,r′2=r2+2π×rad(m)/m,那么基于身份的密钥交换协议RLWE-IDAKE可以显著概率计算出相同的密钥材料kA1=kB1,其不相等概率至多为2n×exp(3δ-πω2),是n的可忽略函数(其中δ<2-n).
证明. 首先,根据协议规范,有:
vB1=guArB+gB1=g(M-1rA+fA)rB+gB1=
gM-1rArB+gfArB+gB1,
vA1=guBrA=g(M-1rB+fB)rA=
gM-1rBrA+gfBrA=vB1+g(fBrA-fArB)-gB1.

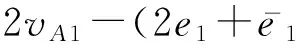
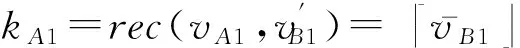
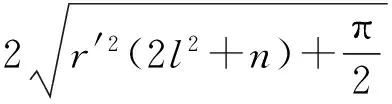

2exp(3δ-πω2).
2nexp(3δ-π×ω2).





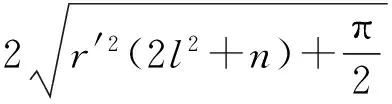
证毕.
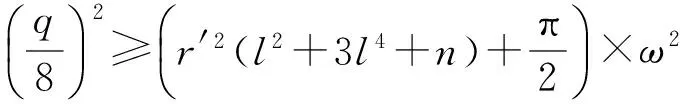
其中,r′2=r2+2π×rad(m)/m,那么基于身份的密钥交换协议RLWE-IDAKE可以显著概率计算出相同的密钥材料kA2=kB2,其不相等概率至多为2n×exp(5δ-πω2),是n的可忽略函数(其中δ≤2-n).
证明. 首先,根据协议规范,有:
vB2=gbArB+gB2=g(IAM1)rB+gB2=
g(IAM-1S+IAe0)rB+gB2=
gIAM-1SrB+gIAe0rB+gB2,
vA2=guBSA=g(M-1rB+fB)(SIA+MeA)=
g(M-1rBSIA+rBeA+SIAfB+MfBeA)=
vB2+g(rBeA+SIAfB+MfBeA-IAe0rB)-gB2.


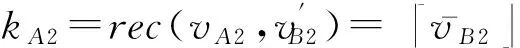

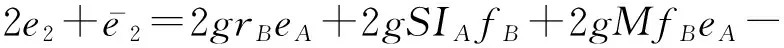


同理,可证明gMfBeA和gIAe0rB的解码基系数服从δ-亚高斯分布,亚高斯分布的系数为l2.


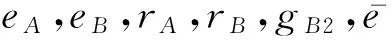

证毕.

其中,r′2=r2+2π×rad(m)/m,那么基于身份的密钥交换协议RLWE-IDAKE可以显著概率计算出相同的密钥材料kA3=kB3,其不相等概率至多为2n×exp(3δ-πω2),是n的可忽略函数(其中δ<2-n).
证明请参考引理7.
3.4 参数设置


则密钥交换协议的错误概率低于ε.
因此,设置q=O(r3×n3lbn),令r=ξq,ξ=α×(5n/lb (5n))1/4,其中:



4 安全性证明
定理3. 如果RLWE问题是困难的,那么RLWE-IDAKE协议在ID-BJM模型下是安全的身份基认证密钥交换协议.具体而言,攻击者A赢得定义4中游戏的优势满足:

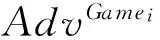
Game0.同定义4的安全游戏,攻击者A赢得游戏Game0的优势定义为

(2)


(3)
Game2.随机选择I,J←[1,N],如果用户J没有被Test查询,则退出游戏,并输出一个随机值,除此之外,与Game1相同.令Event2表示猜测正确这个事件,那么攻击者A赢得游戏Game2的优势为

(4)
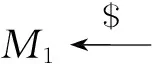
(5)
证毕.
引理10. 如果攻击者A可以区分游戏Game2和Game3,那么可以构造一个区分器D1解决RLWE的一个实例,即已知(M-1,M1)和(Ii,Si),i=1,2,…,N-1,判定M-1和Ii来自RLWE的采样,即M-1和Ii←AS,χ,或者来自于均匀分布U(Rq).
证明. 假设区分器D1的输入为(M-1,M1)和(Ii,Si),i=1,2,…,N-1,如果M-1和Ii来自RLWE的采样,那么D1的输出与Game2相同,如果M-1和Ii来自于均匀分布U(Rq),那么D1的输出与Game3相同.因此,如果A可以区分Game2和Game3,那么D1就可以根据A的输出判决M-1和Ii←AS,χIi来自RLWE的采样,或者来自于均匀分布U(Rq).从而,

证毕.


(6)
引理11. 如果攻击者A可以区分游戏Game3和Game4,那么可以构造一个区分器D2解决RLWE的一个实例,即已知(M-1,uA),判定uA来自RLWE的采样,或者来自于均匀分布U(Rq).
证明. 假设区分器D2的输入为(M-1,uA),如果uA来自RLWE的采样,那么D2的输出与Game3相同,如果uA取值于均匀分布U(Rq),那么D2的输出与Game4相同.因此,如果A可以区分Game3和Game4,那么D2就可以根据A的输出判决uA来自RLWE的采样,或者来自于均匀分布U(Rq).从而:

证毕.

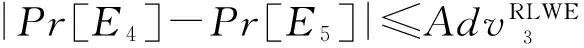
(7)
引理12. 如果攻击者A可以区分游戏Game4和Game5,那么可以构造一个区分器D3解决RLWE的一个实例,即已知(M-1,uB),(guA,vB1)和(gbA,vB2),判定uB,vB1,vB2来自RLWE的采样,或者来自于均匀分布U(Rq).
证明. 证明同引理10.
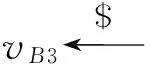

(8)
同时,由于在游戏Game6中,协议公开传输的消息都是随机选择的,因此,协议生成的会话密钥是完全随机的,即攻击者A赢得游戏Game6的概率满足:
(9)
引理13. 如果攻击者A可以区分游戏Game5和Game6,那么可以构造一个区分器D4解决RLWE的一个实例,即已知(gcA,vB3),判定vB3来自RLWE的采样,或者来自于均匀分布U(Rq).
证明. 证明同引理10.
综合式(2)~(9),可以得到

下面,我们对RLWE-IDAKE协议进一步分析.由协议规范可知,用于计算会话密钥的密钥材料包括:
vB1=guArB+gB1∈Rq,
vB2=gbArB+gB2∈Rq,
vB3=gcASB+gB3∈Rq,
分别是由A的临时私钥和B的临时私钥、A的长期私钥和B的临时私钥以及A的长期私钥和B的长期私钥生成的.因此,即使泄露双方的长期私钥也不影响会话密钥的安全性,从而说明该协议满足前向安全性.
5 结束语
本文利用分圆环上的LWE问题设计了身份基认证密钥交换协议,以理想格的解码基为工具,详细分析了协议的容错性能,并给出了合理的参数设置建议.协议在ID-BJM模型下满足AKE安全性和PKG前向安全性,并且在双方长期私钥泄露、双方临时私钥泄露、A的长期私钥和B的临时私钥泄露这3种情况下仍然保证会话密钥安全,但是在A的临时私钥和B的长期私钥泄露的情况下无法实现会话密钥安全,这也是需要进一步研究解决的问题,即如何设计在CK模型中可证明安全的基于格的身份基认证密钥交换协议.
[1]Diffie W, Hellman M. New directions in cryptography[J]. IEEE Trans on Information Theory, 1976, 22(6): 644-654
[2]Shamir A. Identity-based cryptosystems and signature schemes[G] //LNCS 196: Advances in Crypto1984. Berlin: Springer, 1985: 47-53
[3]Chen L, Kudla C. Identity based key agreement protocols from pairings[C] //Proc of the 16th IEEE Computer Security Foundations Workshop. Los Alamitos, CA: IEEE Computer Society, 2002: 219-213
[4]Wang Shengbao, Cao Zhenfu, Dong Xiaolei. Provably secure identity-based authenticated key agreement protocols in the standard model[J]. Chinese Journal of Computers, 2007, 30(10): 1842-1854 (in Chinese)
(王圣宝, 曹珍富, 董晓蕾. 标准模型下可证明安全的身份基认证密钥协商协议[J].计算机学报, 2007, 30(10): 1842-1854)
[5]Gao Haiying. Provable secure id-based authenticated key agreement protocol[J]. Journal of Computer Research and Development, 2012, 49(8): 1685-1689 (in Chinese)
(高海英. 可证明安全的基于身份的认证密钥协商协议[J].计算机研究与发展, 2012, 49(8): 1685-1689)
[6]Ding J, Xie X, Lin X. A simple provable secure key exchange scheme based on the learning with errors problem[OL]. [2015-06-15]. http://eprint.iacr.org/2012/688
[7]Zhang J, Zhang Z, Ding J. Authenticated key exchange from ideal lattices[G] //LNCS 9057: Advance in EuroCrypt2015, Part Ⅱ. Berlin: Springer, 2015: 719-751
[8]Peikert C. Lattice cryptography for the Internet[G] //LNCS 8772: Proc of the 6th Int Conf on Post-Quantum Cryptography 2014. Berlin: Springer, 2014: 197-219
[9]Bos J W, Costello C, Naehrig M, et al. Post-quantum key exchange for the TLS protocol from the ring learning with errors problem[OL]. [2015-06-15]. http://eprint.iacr.org/2014/599
[10]Singh V. practical key exchange for the Internet using lattice cryptography[OL]. [2015-06-15]. http://eprint.iacr.org/2015/138
[11]Lyubashevsky V, Peikert C, Regev O. A toolkit for ring-LWE cryptography[G] //LNCS 7881: Advance in EuroCrypt2013. Berlin: Springer, 2013: 35-54
[12]Lyubashevsky V, Pikert C, Regev O. On ideal lattices and learning with errors over rings[G] //LNCS 6110: Advance in EuroCrypt2010. Berlin: Springer, 2010: 1-23
[13]Applebaum B, Cash D, peikert C, et al. Fast cryptographic primitives and circular-secure encryption based on hard learning problems[G] //LNCS 5677: Advance in Crypto2009. Berlin: Springer, 2009: 595-618

Zhao Xiufeng, born in 1977. Associate professor. Received her PhD degree from Shandong University. Her main research interests include cryptography protocols and lattice-based cryptography.

Gao Haiying, born in 1978. Associate professor. Received her PhD degree from Beijing University of Posts and Teleco-mmunications. Her main research interests include cryptology theory and provable secure theory.

Wang Ailan, born in 1966. Associate professor. Her main research interests include cryptology theory and algebraic number theory.
An Identity-Based Authenticated Key Exchange Protocol from RLWE
Zhao Xiufeng, Gao Haiying, and Wang Ailan
(PLAInformationEngineeringUniversity,Zhengzhou450001)
Key exchange protocol allows two or more users to compute share session key via exchange information in the open communication channel, and uses the session key to finish cryptography tasks, such as secure communication and authentication. Recently, it becomes a hotspot research question that how to design authenticated key exchange protocol with lattice-based one-way function. Several lattice-based two-party authenticated key exchange protocols have been proposed. However, how to extend them to the identity-based cryptography background still remains open question. In this paper, an identity-based authenticated key exchange protocol from the learning with errors (LWE) problem over cyclotomic ring is proposed. The protocol generates master key by ring LWE (RLWE) sample algorithm, and further extracts the users’ secret key, and computes key materials which derive the share session key via exchanging Diffie-Hellman ephemeral key. The protocol introduces error item, uses encoding bases of ideal lattice as the tool for analyzing error tolerance, and makes reasonable suggests for parameters setting. The protocol achieves provable AKE secure and PKG forward secure in the ID-BJM model. Furthermore, the session key is also secure even if both long private keys are leaked or both ephemeral private key are leaked orA’s ephemeral key andB’s long private key are leaked.
cyclotomic ring; ring learning with errors (RLWE); provable secure; identity-based cryptography; key-exchange protocol
2015-06-16;
2015-11-23
国家自然科学基金项目(61272488,61272041,61202491,61601515)
TP309
This work was supported by the National Natural Science Foundation of China (61272488, 61272041, 61202491, 61601515).

