碳纤维多层立体织机引纬机构振动动力学仿真
杨建成,李 浩,蒋秀明
(1.天津工业大学 机械工程学院,天津 300387;2.天津工业大学 天津市现代机电装备技术重点实验室,天津300387;3.天津工业大学 天津市机械基础及纺织装备设计虚拟仿真实验教学中心,天津 300387)
碳纤维多层立体织机引纬机构振动动力学仿真
杨建成1,2,3,李 浩1,2,3,蒋秀明1,2,3
(1.天津工业大学 机械工程学院,天津 300387;2.天津工业大学 天津市现代机电装备技术重点实验室,天津300387;3.天津工业大学 天津市机械基础及纺织装备设计虚拟仿真实验教学中心,天津 300387)
针对现有碳纤维立体织机引纬机构剑杆高速运动振动剧烈、运动稳定性不佳的弊端,以Adams平台为基础,建立立体织机引纬机构的动力学模型,根据Hertz接触理论来考虑齿轮齿条的动态啮合过程,对立体织机引纬机构采用正弦运动规律和修正梯形运动规律的动力学性能进行仿真对比分析.仿真分析结果表明:相比采用不同运动加速度规律,由于齿轮齿条啮合产生的啮合力冲击对引纬机构的振动影响更大,是剑杆产生振动的主要原因.
碳纤维;立体织机;引纬机构;动力学
碳纤维及其立体织物的复合材料具有一系列优异的性能,近年来在航空航天、汽车、能源、交通、运动器材等众多领域得到迅速推广发展.碳纤维立体织造设备的设计研究是应用碳纤维及其立体织物复合材料的重要基础[1].
引纬是织造中的关键工艺环节,立体织机引纬机构的引纬动作由齿轮齿条传动驱动完成,与传统平面织机采用连杆或者连杆凸轮引纬机构不同.引纬机构采用刚性剑杆引纬,剑杆在进入梭口后不需要导向装置,依靠剑杆自身的刚度保持平直,将织物引到对侧,引纬过程中剑头剑杆均不与开口的经纱接触.可以很好的保护织物纤维,保证织造质量,对于织造高性能纤维织物时如碳纤维织物具有重要意义[2].刚性剑杆与机架靠剑杆尾部的滑块连接,相当于悬臂梁结构.实际操作中发现,刚性剑杆在引纬运动过程中会发生较为明显的振动,当剑杆的振动剧烈时,剑头就会刺伤织物经纱,造成经纱纤维的磨损,使织口经纱发生刮纱和起毛现象,导致织口堵塞及开口不清等严重影响织造质量的问题.因此需要在现有基础上对剑杆的振动问题进行研究分析.潘宏根研究表明,剑杆的轴向振动对于剑杆的位移和应力影响都比较小[3].冯志华基于kane方程及假设模态建立了刚性建刚纵横振动的非线性动力学控制方程,并对刚性剑杆的动力稳定性进行初步分析研究[4-5].由于立体织机的特殊性,鲜有对于齿轮齿条型引纬引纬机构的研究,本文将对不同的加速度运动规律下剑杆运动进行动力学模拟仿真,对剑杆振动的原因进行分析探讨.
1 剑杆振动原因初步分析
图1为立体织机采用的引纬机构.机构通过伺服电机驱动齿轮齿条机构,使安装在齿条上的刚性剑杆完成往复引纬动作;采用丝杠传动调节传剑机构上下运动完成不同层面的引纬.
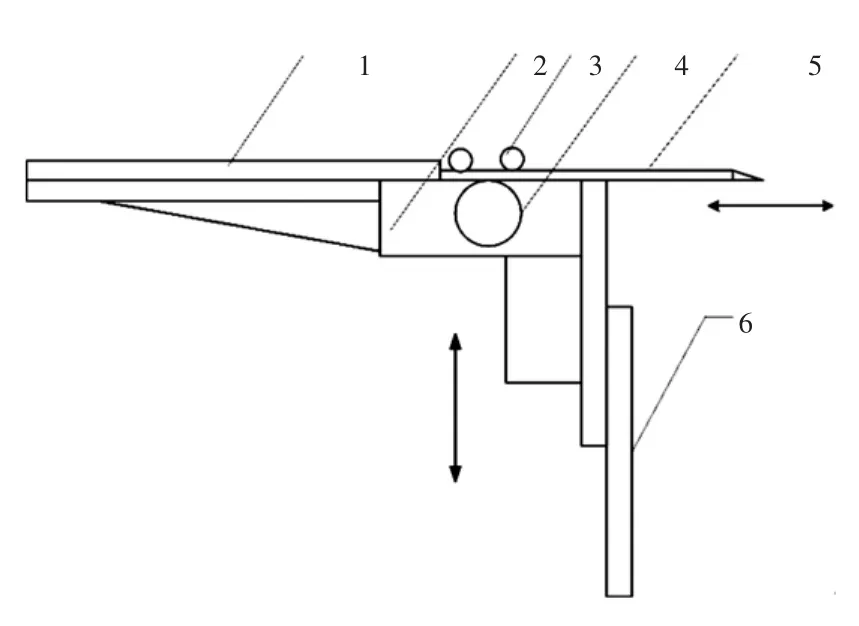
图1 碳纤维立体织机引纬机构示意图Fig.1 Structure of weft insertion mechanism of carbon fiber multilayer loom
由于引纬机构的升降运动与剑杆的伸出运动先后进行,彼此独立,互相之间影响微小.所以这里只考虑剑杆引纬动作,因此建立剑杆运动动力学模型如图2所示.
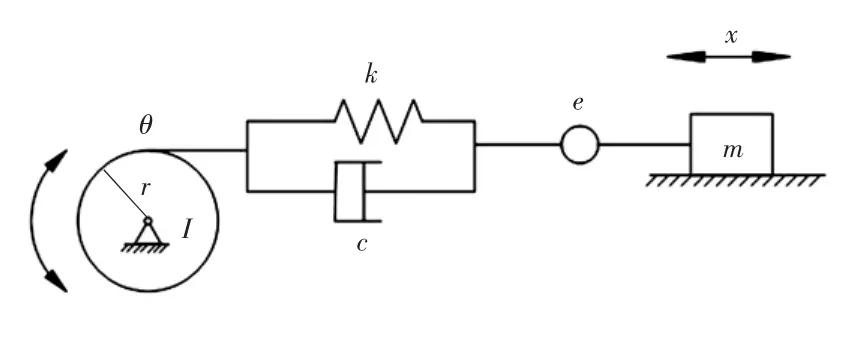
图2 剑杆引纬动力学模型Fig.2 Dynamic model of weft insertion mechanism
该模型只考虑齿轮齿条啮合时的变形,忽略啮合侧隙的非线性变化.
图2中:x为剑杆往复运动位移;m为剑杆质量;e为齿轮齿条啮合侧隙;k为齿轮齿条啮合的综合刚度;c为齿轮齿条啮合的阻尼系数,在此设为定值;θ为齿轮角位移;I为齿轮的转动惯量;r为齿轮的节圆半径.
这里考虑齿轮齿条啮合时齿轮副处的变形,设齿轮齿条啮合时,在沿啮合线的方向想,齿轮齿条啮合变形为σ,由模型可得

式中:α为齿轮齿条啮合压力角.
建立平衡方程为:

得到剑杆运动的动力学微分方程为:
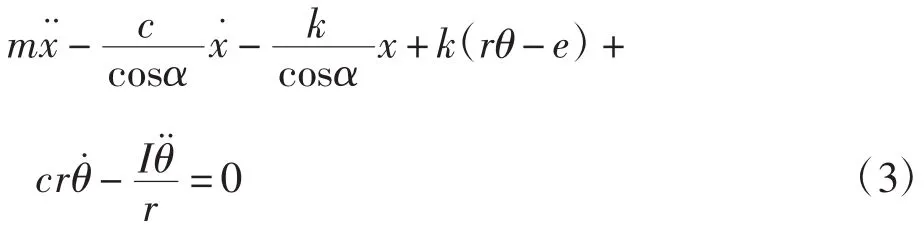
由式(3)看出,时变综合啮合刚度和引纬齿轮的转速及加速度都会影响剑杆运动加速度的变化.即使齿轮转速或者加速度恒定,由于时变综合啮合刚度k的变化,也会使剑杆运动加速度出现波动.及齿轮转动角加速度的变化,都会引起剑杆运动加速度的变化.
齿轮传动由于轮齿的综合啮合刚度不仅具有时变性,而且具有很大的突变性,并且轮齿啮合为动态碰撞冲击过程,将导致齿轮传动产生振动[6],这种振动对高速运动的机构的动力性能和稳定性都存在不良影响.文献[7-9]的研究表明,齿轮齿条的动态啮合将导致啮合力频繁波动,使齿轮角加速度波动.变工况冲击引起的瞬态齿轮动态啮合力具有幅值大、冲击作用时间短等特点[10],在齿轮转速不断变化的情况下,加速度波动将更加剧烈,从而导致机构的振动.在此引纬机构中,齿轮齿条啮合的振动将直接反映到与齿条连接在一起的齿条上.
引纬剑杆长度达到1.5 m,剑杆与织机靠剑杆尾部的滑块连接,相当于悬臂梁结构,实际剑杆并不是严格刚体,剑杆并不是平直状态,而是会产生竖直方向上的挠度位移.因此剑杆轴向运动的加速度会直接引起剑杆前端挠度大的部分产生纵向惯性力,从而使剑杆产生竖直方向上的振动位移,如果加速度变化,则相当于在剑杆前端产生一个竖直方向上的不断变化的激励,使剑杆产生振动.因此剑杆轴向运动的速度和加速度等运动参数影响剑杆运动的平顺性,当剑杆采用不同运动规律时,剑杆运动的速度和加速度分布和峰值不同,不恰当的运动规律会导致机构振动等问题.
因此,引纬剑杆的运动规律的选择以及齿轮齿条的啮合是影响剑杆运动的原因.立体织机引纬机构由齿轮齿条机构组成,因此,齿轮啮合的影响不可避免,但是引纬剑杆的运动规律可以灵活的选择和设计.常用的剑头运动规律有正弦加速度规律、梯形加速度规律和修正梯形加速度规律等.研究表明,在运动动程和运动时间相同的条件下,目前常用的剑头运动规律中,修正梯形加速度运动规律是最优越的[11-12].本文将以Adams平台为基础,对立体织机引纬机构采用常用的正弦运动规律和修正梯形运动规律进行仿真对比分析.
2 三维模型建立及数据转换
图3所示为立体织机采用的引纬机构.机构中齿轮齿数为47,模数为4 mm,齿厚为10 mm,齿条齿厚为10 mm,压力角为20°,材料为碳钢Q235.
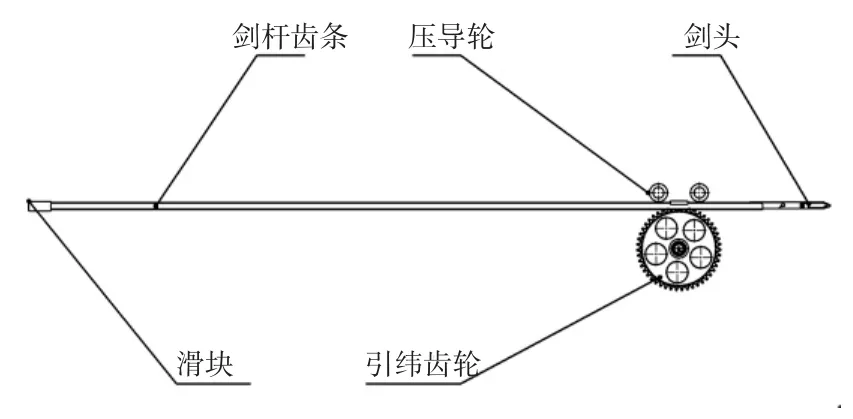
图3 立体织机引纬机构Fig.3 Weft insertion mechanism of carbon fiber multilayer loom
利用三维建模软件Solidworks建立引纬机构个零件实体模型,整体装配后,检查装配正确无干涉,建立立体织机引纬机构模型如图4所示.

图4 立体织机引纬机构模型Fig.4 Solidworks model of carbon fiber multilayer loom
在Adams中仿真时,零部件的一些特征,如倒角、圆角等对于机构的动力学仿真没有影响,却会使模型数据臃肿,导致仿真分析效率低下.因此,在进行模型数据转换之前,将倒角、圆角等对仿真分析无益的特征删除,保留必要的模型特征数据.
Solidworks与Adams之间数据转换接口不稳定易出错,因此采用中间数据格式将模型数据导入Adams软件中.STEP标准具有简便、可兼容性、寿命周期长和可扩展性的优点,能够很好的解决信息集成问题,实现资源的最优组合,实现信息的无缝连接[13].
在solidworks中奖模型数据另存为step格式,然后进入Adams中选择导入step格式数据,将step格式的引纬机构模型数据导入到Adams软件中.
3 建立引纬机构动力学仿真模型
3.1 Adams动力学模型建立
将模型导入Adams后,需要定义各零部件的约束和载荷、接触对以及驱动[14].动力学模型如图5所示.

图5 立体织机引纬机构Adams动力学模型Fig.5 Dynamic model of weft insertion mechanism of carbon fiber multilayer loom
3.2 剑杆引纬运动规律
剑杆采用正弦加速度运动规律时,引纬齿轮角位移规律为2πtsin(2πt-π/2)rad.
剑杆采用修正梯形加速度时,按照文献[12]提出的方法从数学角度出发,根据引纬规律的要求,直接假设位移曲线的方程,然后根据位移、速度、加速度的关系以及引纬规律加速度曲线要求连续光滑的条件,对各段曲线列出边界条件,列出方程组进行求解[15].
如图6所示,x轴为运动时间,y轴为加速度.曲线分为OA、AB、BC、CD、DE、EF、EG这7段,设AB、CD、EF段加速度值为am1、am2、am3.根据文献的方法,可以求得加速度曲线的方程.
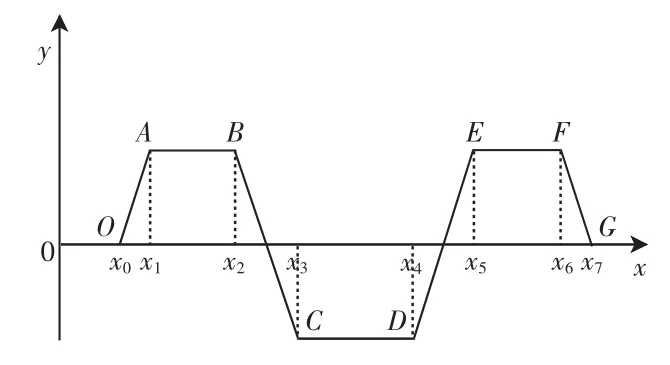
图6 修正梯形加速度运动规律曲线Fig.6 Motion law of modified trapezoidal acceleration
设加速度曲线方程为
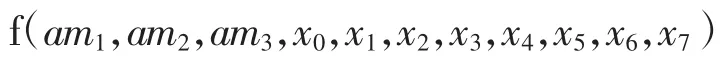
为保证采用修正梯形加速度运动规律时引纬机构的行程和引纬时间一致,取计算参数取值如表1所示,于是得到2种运动规律加速度曲线如图7所示.

表1 修正梯形加速度曲线参数表Tab.1 Modified trapezoidal acceleration curreparameter
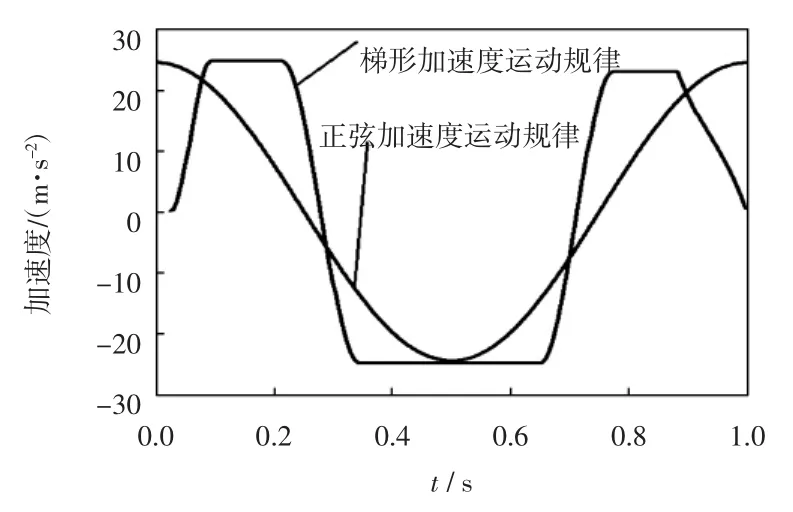
图7 2种运动规律加速度曲线Fig.7 Motion law of modified trapezoidal accelerationand sine acceleration
利用Matlab编程实现方程曲线的计算和数据的输出.根据引纬齿轮尺寸参数转换为角位移运动规律数据,然后将角位移运动规律数据导出txt文本格式.
在Adams中导入实验数据并生成样条数据[16],然后再引纬齿轮相对地面旋转副添加旋转驱动,利用导入生成的样条数据定义旋转角位移.
3.3 接触载荷的确定
齿轮齿条在啮合过程中,齿面接触碰撞产生力,为模拟真实情况,齿轮齿条的啮合采用接触方法来模拟.Adams平台计算接触力常用冲击函数法(Impact).触力计算表达式为:
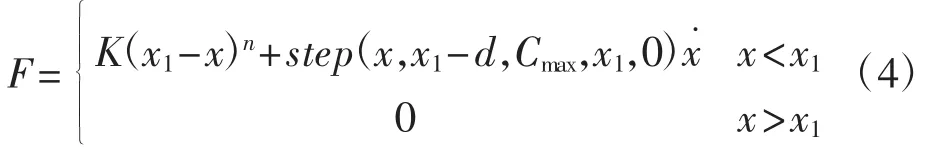
式中:K为接触刚度系数;d为阻尼达到最大时两接触物体的穿透深度;Cmax为最大接触阻尼;˙为穿透速度;n为非线性弹性力幂指数.
根据Hertz接触理论,假设两接触面为圆柱体外圆表面时,有

其中:
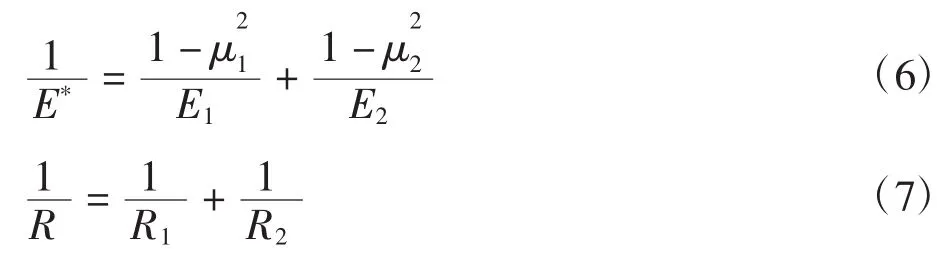
式中:δ为相互接触两个物体对应点接近的距离;F为两轮齿间载荷;R1、R2分别为碰撞点处两物体的曲率半径;E1、E2分别为两物体的材料弹性模量;μ1、μ2分别为两物体的材料泊松比[17].
由式(5)得知:

4 引纬机构动力学仿真计算
根据式(9)计算,齿轮齿条接触刚度设为1460.814 N/m,阻尼系数设为0.01 N·s/m,非线性弹性力指数设为1.5,最大穿透深度设为0.01 mm.积分求解器设为GSTIFF,积分格式为SI2[18].仿真时间1 s,仿真步数5 000.仿真得到以剑头质心为参考点,剑杆运动规律曲线如图8到图13所示.
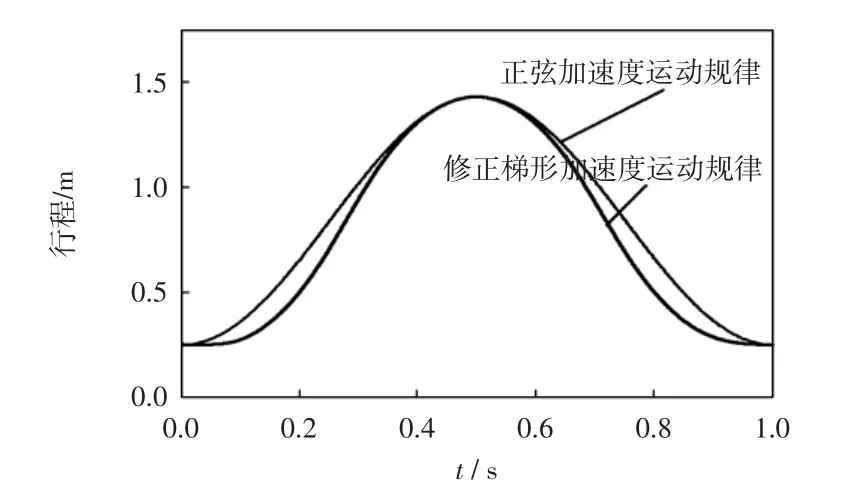
图8 剑头位移曲线Fig.8 Displacement curves of gripper head
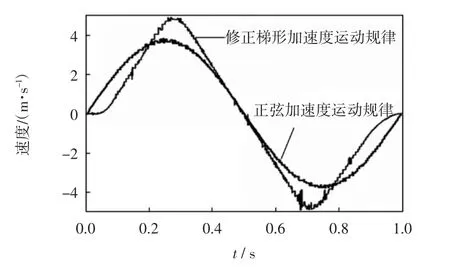
图9 剑头速度曲线Fig.9 Velocity curves of gripper head
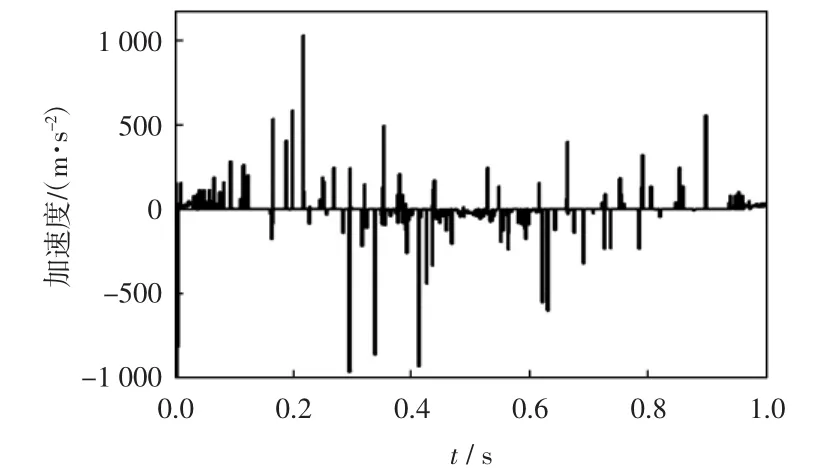
图10 正弦加速度运动规律剑头加速度曲线Fig.10 Acceleration curve of gripper head in law of sinusoidal acceleration
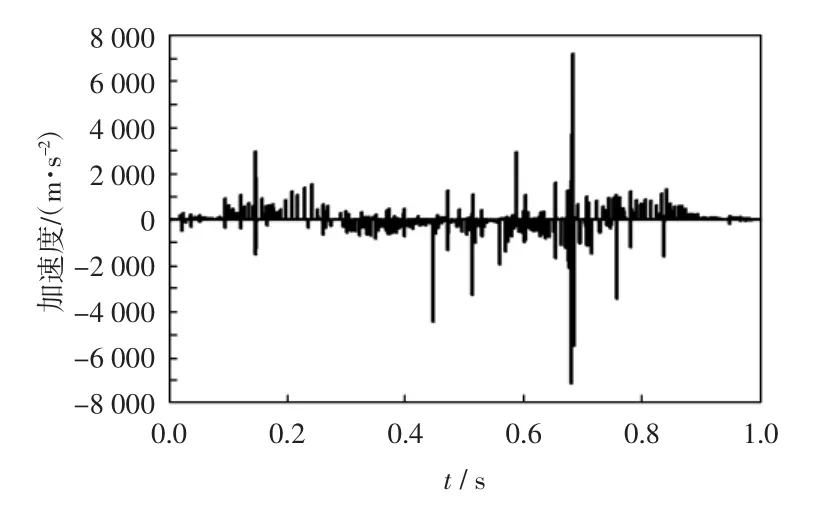
图11 修正梯形加速度运动规律剑头加速度曲线Fig.11 Acceleration curve of gripper head in law of modified trapezoid l acceleration
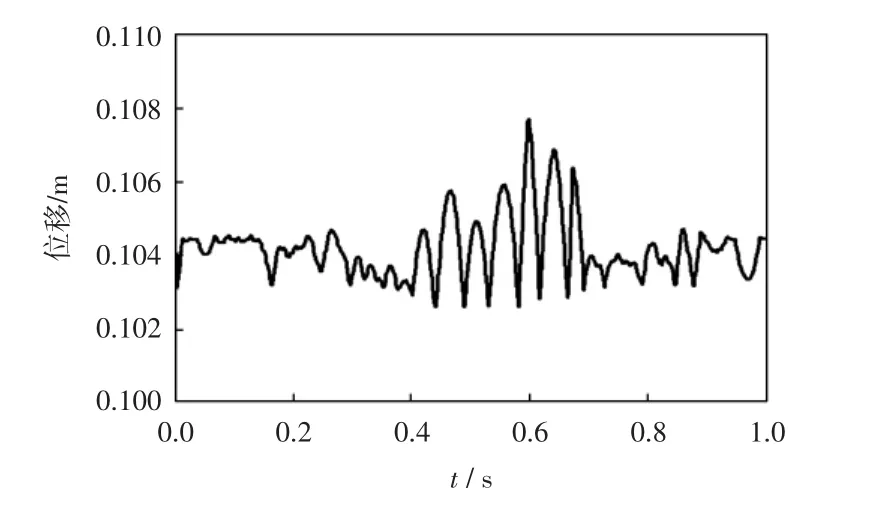
图12 正弦加速度运动规律剑头Y向位移曲线Fig.12 Displacement curve of gripper head in law ofsinusoidal acceleration
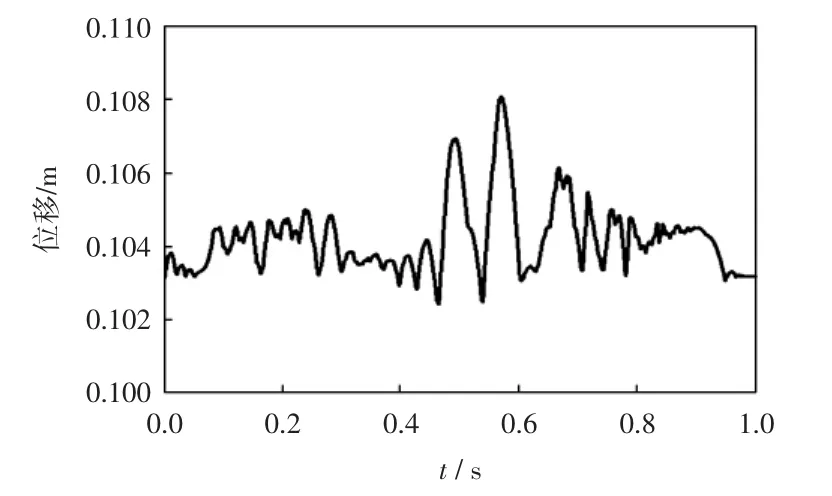
图13 修正梯形加速度运动规律剑头Y向位移曲线Fig.13 Displacement curve of gripper head in law of modified trapezoid l acceleration
5 结果分析
在引纬初始阶段,由图7可知,修正梯形加速度曲线由零开始,启动过程没有惯性冲击;而正弦加速度运动规律加速度不是由零开始而是直接达到加速度峰值,会造成启动冲击.但是由于初始阶段剑杆并未伸出,启动阶段剑杆的振动较小.由图12和图13可以看出,2种运动规律下,剑头在启动阶段的竖直方向振动位移基本相同,启动冲击并没有给剑杆的振动造成明显影响.在剑杆进入梭口后,随着剑杆的伸出,剑杆挠度变大,剑杆自身刚度带来的影响变大.两种加速度运功规律均光滑连续,不会造成惯性冲击.齿轮齿条啮合会造成啮合冲击,由于啮合速度不断变化,是变工况啮合,变工况啮合冲击具有时间短,冲击幅值大的特点.因此,图11和图12加的速度曲线会在局部出现幅值的显著波动,并且由于修正梯形的速度峰值较大,齿轮啮合速度较大,因此引起的啮合冲击较大,所以图11中修正梯形加速度曲线的局部加速度冲击波动比较大.图12和图13中,剑头竖直方向上振动位移最大值分别为0.107 m和0.108 m,可以看出,由于修正梯形运动规律速度峰值较大,引起的啮合冲击较大,因此剑头的振动也更为强烈.
6 结论
本文对立体织机引纬剑杆的振动原因进行分析讨论,并通过Adams平台对立体织机引纬机构分别采用正弦加速度运动规律和修正梯形加速度运动规律时,机构的动力性能进行模拟仿真,结果表明:相比采用不同运动加速度规律,由于齿轮齿条啮合产生的啮合力冲击对引纬机构的振动影响更大,是剑杆产生振动的主要原因.仿真分析结果为进一步研究立体织机引纬机构的动力学性能以及振动特性分析奠定了基础,指明了研究方向.
[1]杨建成.碳纤维多层角联机织装备及技术[J].纺织机械,2014,30(4):88-89. YANG J C.Multilayer carbon fiber angle interlocking woven equipment and technology[J].Textile Machinery,2014,30(4):88-89(in Chinese).
[2]代金友.剑杆织机的发展趋势与品种适应性[J].科技信息,2012(14):428. DAI J Y.Development trend and variety adaptability of Rapier loom[J].Science,2012(14):428(in Chinese).
[3]潘宏根.剑杆的弹性振动[J].中国纺织大学学报,1987,12(5):135-140. PAN H G.Elastic vibration of Rapier[J].Journal of China Textile University,1987,12(5):135-140(in Chinese).
[4]冯志华.刚性剑杆的动力稳定性I:非线性动力学建模[J].机械设计,2002,23(12):28-30,42. FENG Z H.Dynamic stability of rigid rapiers I:nonlinear dynamic modeling[J].Journal of Machine Design,2002,23(12):28-30,42(in Chinese).
[5]冯志华,钱志良,吉迎冬,等.刚性剑杆的动力稳定性Ⅱ:稳定性分析[J].机械设计,2003,24(5):31-33. FENG Z H,QIAN Z L,JI Y D,et al.Dynamic stability of rigid rapiers II:stability analysis[J].Journal Of Machine Design,2003,24(5):31-33(in Chinese).
[6]孙月海,张策,潘凤章,等.直齿圆柱齿轮传动系统振动的动力学模型[J].机械工程学报,2000,36(8):47-50,54. SUN Y H,ZHANG C,PAN F Z,et al.Dynamic model of a spur gear transmission system vibration[J].Chinese Journal of Mechanical Engineering,2000,36(8):47-50,54(in Chinese).
[7]毕凤荣,崔新涛,刘宁.渐开线齿轮动态啮合力计算机仿真[J].天津大学学报:自然科学与工程技术版,2005,38(11):991-995. BI F R,CUI X T,LIU N.Computer simulation for dynamic meshing force of involute gears[J].Journal of Tianjin University:Nature Science and Engineering Technology,2005,38(11):991-995(in Chinese).
[8]黄中华,张晓建,周玉军.渐开线齿轮啮合碰撞力仿真[J].中南大学学报:自然科学版,2011,42(2):379-383. HUANG Z H,ZHANG X J,ZHOU Y J.Simulation of contact force of involute gear meshing[J].Journal of Central SouthUniversity:ScienceandTechnology,2011,42(2):379-383(in Chinese).
[9]洪清泉,程颖.基于ADAMS的多级齿轮传动系统动力学仿真[J].北京理工大学学报,2003,23(6):690-693. HONG Q Q,CHENG Y.Dynamic simulation of multi-stage gear train system in ADAMS [J].Transactions ofBejing Institute of Technology,2003,23(6):690-693(in Chinese).
[10]冯海生,王黎钦,郑德志,等.考虑变工况冲击的齿轮动态啮合力分析[J].振动、测试与诊断,2015,35(2):212-217,394. FENGH S,WANG L Q,ZHENG D Z,et al.Analysis of gear dynamic meshing force considering variable condition impact[J].Journal of Vibration,Measurement&Diagnosis.2015,35(2):212-217,394(in Chinese).
[11]赵雄,胡宇龙,林万焕,等.剑杆织机新型引纬运动学曲线的构造及应用[J].浙江理工大学学报,2010,28(4):556-560,589. ZHAO X,HU Y L,LIN W H,et al.Establishment and application of new weft insertion kinmatics curves on rapier loom[J].Journal of Zhejiang Sci-Tech University,2010,28(4):556-560,589(in Chinese).
[12]陈普生,何敏英.动态综合时剑杆运动规律的选择[J].中国纺织大学学报,1987,12(1):65-70. CHEN P S,HE M Y.Choice of dynamic motion of rapier[J]. Journal of China Textile University,1987,12(1):65-70(in Chinese).
[13]FEENEY A B,FRECHETTE S P,SRINIVASAN V.A portrait of an ISO STEP tolerancing standard as an enabler of smart manufacturing systems[J].Journal of Computing&Information Science in Engineering,2015.
[14]郭会珍,谭长均,陈俊锋.基于ADAMS的行星轮系动力学仿真[J].机械传动,2013,39(5):86-89. GUO H Z,TAN C J,CHEN J F.Dynamics simulation of planetary gear train based on ADAMS[J].Journal of Mechanical Transmission,2013,39(5):86-89(in Chinese).
[15]周香琴.设计引纬曲线的一种简便方法[J].纺织学报,2002,21(1):31-33. ZHOU X Q.A Convenient method of designing rapier movement[J].Journal of Textile Research,2002,21(1):31-33(in Chinese).
[16]赵晓亮.跨坐式单轨交通列车动力学仿真研究[D].北京:北京交通大学,2008. ZHAO X L.Dynamic simulation of straddle-type monorail train[D].Beijing:Beijing Jiaotong University,2008(in Chinese).
[17]LANKARANI H M,NIKRAVESH P E.Continuous contact force models for impact analysis in multibody systems[J].Nonlinear Dynamics,1994,5(2):193-207.
[18]于殿勇,钱玉进.基于ADAMS动力学仿真参数设置的研究[J].计算机仿真,2006,23(9):103-107. YU D Y,QIAN Y J.Parameter-setting for the dynamic simulation based on ADAMS[J].Computer Simulation,2006,23(9):103-107(in Chinese).
Dynamic simulation of weft insertion mechanism of carbon fiber multilayer loom
YANG Jian-cheng1,2,3,LI Hao1,2,3,JIANG Xiu-ming1,2,3
(1.School of Mechanical Engineering,Tianjin Polytechnic University,Tianjin 300387,China;2.Tianjin Key Laboratory of Modern Mechanical and Electrical Equipment Technology,Tianjin Polytechnic University,Tianjin 300387,China;3.Tianjin Virtual Simulation and Experiment Teaching Center of Basic Machinery and Textile Equipment Design,Tianjin Polytechnic University,Tianjin 300387,China)
In view of the poor stability of the existing weft insertion mechanism of carbon fiber multilayer loom,a dynamic model of weft insertion mechanism of carbon fiber multilayer loom is built up based on Adams according to Hertz contact theory with considering dynamic meshing of the gear and rack.The dynamic model is simulated with motion law of sinusoidal and modified trapezoid and the dynamic performance of the two different motion law are compared and analyzed.The result shows that the main factors affecting the vibration properties of weft are the meshing impact of rack and pinion grearing in condition of continuous changes of rapier weft insertion rate.The motion law work on this rack and gear mechanism has relatively small effect on the vibration of the rapier.
carbon fiber;multilayer loom;weft insertion mechanism;dynamic
TS103.134
A
1671-024X(2016)05-0083-06
10.3969/j.issn.1671-024x.2016.05.015
2015-11-30
国家十二五科技支撑项目(2011BAF08B00)
杨建成(1962—),男,博士,教授,主要研究方向为纺织机械设计机器自动化.E-mail:yjc589@163.com

