Prediction of shock-layer ultraviolet radiation for hypersonic vehicles in near space

Niu Qinglin,He Zhihong,Dong Shikui

School of Energy Science and Engineering,Harbin Institute of Technology,Harbin 150001,China

Prediction of shock-layer ultraviolet radiation for hypersonic vehicles in near space

Niu Qinglin,He Zhihong,Dong Shikui*

School of Energy Science and Engineering,Harbin Institute of Technology,Harbin 150001,China

A systemic and validated model was developed to predict ultraviolet spectra features from the shock layer of near-space hypersonic vehicles in the ''solar blindquot;band region.Computational procedures were performed with 7-species thermal non-equilibrium fluid mechanics,finite rate chemistry,and radiation calculations.The thermal non-equilibrium flow field was calculated with a two-temperature model by the finite volume technique and verified against the bow-shock ultra-violet (BSUV) flight experiments.The absorption coefficient of the mixture gases was evaluated with a line-by-line method and validated through laboratory shock tube measurements.Using the line of sight (LOS) method,radiation was calculated from three BSUV flights at altitudes of 38,53.5 and 71 km.The investigation focused on the level and structure of ultraviolet spectra radiated from a NO band system in wavelengths of 200–400 nm.Results predicted by the current model show qualitative spatial agreement with the measured data.At a velocity of 3.5 km/s (about Mach 11),the peak absolute intensity at an altitude of 38 km is two orders of magnitude higher than that at 53.5 km.Under the same flight conditions,the spectra structures have quite a similar distribution at different viewing angles.The present computational model performs well in the prediction of the ultraviolet spectra emitted from the shock layer and will contribute to the investigation and analysis of radiative features of hypersonic vehicles in near space.

1.Introduction

In recent years,near-space aircraft have aroused great interest because of their high success rates for penetration,hence the development of many hypersonic vehicle programs,such as United States' ''HTV-2quot; and ''X-37Bquot;,Russia's ''Clipperquot;,Japan's ''Hopequot;,and England's ''HOTOLquot;.When these aircraft glide through the Earth's atmosphere at incredibly fast speeds,the high-temperature shock layer around the vehicle surface will produce intense emissions accompanied with complex physical and chemical processes such as dissociation,ionization,recombination and chemiluminescence.It is understood that within the features of emission spectra from the shock layer,great attention should be paid to photo-electric offensive and defensive strategies.In practice,the detection of theater targets utilizes the mid-wave infrared(IR)spectral region(3–5 μm as a baseline and distinctive ultraviolet (UV) or visible spectral regions as a second detection band).1Note that,in the so-called''solar blindquot;band covering 200–300 nm,the dark sky background allows one to detect a vehicle as a signature source against a very low background with a striking contrast.2In this typical band region,ultraviolet emissions from the shock layer have great potential for the early warning systems (EWS),target intercept guidance techniques to monitor,identify and track unfriendly aircraft,and also for suppression of radiative noise through the optical window.3,4In support of these concepts,two bow-shock flight experiments were conducted at relatively low velocities(about 3.5 km/s)5and high velocities(about 5.1 km/s)6at different altitudes by the Innovative Science and Technology Office in 1990s,and a series of the spectra signal data were obtained.These are helpful to understand the mechanisms of the shock-layer ultraviolet emission and to calibrate computational models.7–12In a two-color detection strategy,the ultraviolet signature may offer many advantages over long wavelength systems in reducing false alarm rates,and as a supplementary technique for near-space hypersonic aircraft use in offensive and defensive confrontations;hence,it is of great significance to investigate the ultraviolet emission features in the shock layer by a high fidelity numerical approach.

The purpose of this work is to develop an efficient model for prediction of shock-layer ultraviolet spectral radiation characteristics during hypersonic vehicle glide in the Earth's atmosphere.In fluid computations,a two-temperature model will be employed in the treatment of the non-equilibrium flow field of the shock layer,and a 7-species scheme is also considered,which consists of a mixture of ions,electrons,atoms and molecules at high temperature(O2,N2,O,N,NO,NO+and e-).Navier-Stokes equations incorporating finite rate chemical kinetics are solved with the finite volume technique.For comparison with previous literature,cases at three altitudes will be investigated:38,53.5 and 71 km.In radiation models,in particular NO gamma and delta band systems,the radiative transition mechanisms of gas molecules are taken into account to predict spectra within wavelengths of 200–400 nm.In addition,the non-equilibrium population of the electronic state of species is characterized by a three-temperature model,and the absorption coefficient of mixture gases is evaluated with a line-by-line method.Considering the BSUV flights as the focus of this research,the radiative transfer equation (RTE) is integrated with the line of sight (LOS) method.We will compare the computational results of each module with a wide set of experimental data,and analyze the structure and level of the ultraviolet spectra emitted from the bow-shock layer in different flight cases.

2.Available experimental data

Two BSUV flight experiments5,6were developed by the Innovative Science and Technology Office of the Strategic Initiative Organization in the 1990s in order to validate certain issues with hypersonic vehicles at low and high altitudes.These included the spectral distribution and intensity of ultraviolet radiation emitted from the bow-shock layer around the nose cone,the plume exhausted from rocket motors,vehicle aerodynamics,and gas radiative noise in the optics window.In the BSUV experiments,instruments in the payload,with a half cone angle of 15°and a 0.1016 m-radius dome,consisted of a scan spectrometer,eight optic photometers,an electro density microprobe,and two vacuum ultraviolet (VUV) photometers.The forward structure of the vehicle can be seen in Fig.1,and the arrangement of detectors in the payload shown in Fig.2.The spectrometer is used to measure the emission intensity as a function of the wavelengths within 200–400 nm.Photometers,as a redundancy and supplement to the spectrometer,are arranged with viewing angles of 0°,30°and 50°from the vehicle centerline and used to individually detect spectra variations with the precession during flights.Each photometer is employed to identify spectral features of one particular molecule near the center wavelength λ0,such as NO(λ0=215 nm and 230 nm),OH radical(λ0=310 nm)and(λ0=391 nm).A series of spectral profiles of ultraviolet emissions created in the bow-shock layer,covering 38–70 km at 3.5 km/s and 100–65 km at 5.1 km/s,are available to validate computational models of radiation.

3.Numerical models

Broadly speaking,there are four parts to predicting the ultraviolet radiation emitted from high-temperature shock layers around a vehicle13:(1)flow field;(2)population of the exited electronic states;(3)spectra parameters;and(4)radiative transfer calculation.These can be obtained through three methods:multi-species thermo-chemical non-equilibrium fluid mechanics,multi-temperature non-equilibrium radiation modules,and radiative transfer calculation procedures.

Fig.2 The layout of BSUV's detectors from Ref.5.

3.1.Governing equations of flow field

Assuming that the flow is based on a continuum approximation,we use a blunted cone as an object to investigate the chemical and thermodynamic non-equilibrium hypersonic flow.Axisymmetric Navier-Stokes equations for a nonequilibrium mixture of chemically reacting gases coupled with conservation equations for electronic states of molecules are expressed as:

where Q is the conservative variable vector,EC,FCand HCare vectors of the convective fluxes,ED,FDand HDrepresent vectors of the viscous fluxes,and S is the source term.The internal energy,though related to all molecular species,can be represented by one internal temperature equal to vibrationalelectronic temperature.That is to say,the internal energy source term is based solely on the vibrational internal energy.Hence,each vector in Eq.(1)is given in the following matrix:

where

and Yiis the mixture mass fraction of the ith species,Dithe diffusion coefficient,ρ the mixture density,p the pressure,T the translational temperature,Tvibthe inner/vibrational temperature,κ the thermal conductivity of the gas,and Nsis the number of different species.For calorically perfect gases,the translational temperature falls into the scope of the Sutherland law determined from the equation and used to calculate the viscosity.

Given a Newtonian fluid and the Stokes' hypothesis,shear stress terms can be given as follows:

where u and v are components of velocity vector V in Cartesian coordinates(x,r),and μ the viscous coefficient of the nonequilibrium mixture.

Similarly,qr,qint,rand τrrare obtained.

For thermal non-equilibrium with mixing and reacting 7-species gas including N2,O2,N,O,NO,NO+and e-,the total energy per volume is expressed as:

where evib,kis the vibrational energy of the kth molecular component per unit mass,and hf,iis the reference heat of formation.

Without considering the electronic energy of the molecule,translational-rotational and vibrational heat capacities for species i are expressed respectively as:

where the molecular degrees of freedom ξ for each species have fixed values 0,for O,e-and N,and 2 for others.Ruis the universal gas constant.

Internal energy per unit of mass can be a function of characteristic parameters of species i with characteristic vibrational temperature θvsmand the number of degeneracy states in the maximum value of Nd,as follows:

Mixture transport properties,such as dynamic viscosity and thermal conductivity,can be calculated with Wilke's semi-empirical method according to species viscosities,as determined by Bird's formula14,and Eucken's assumption15for the species conductivities.

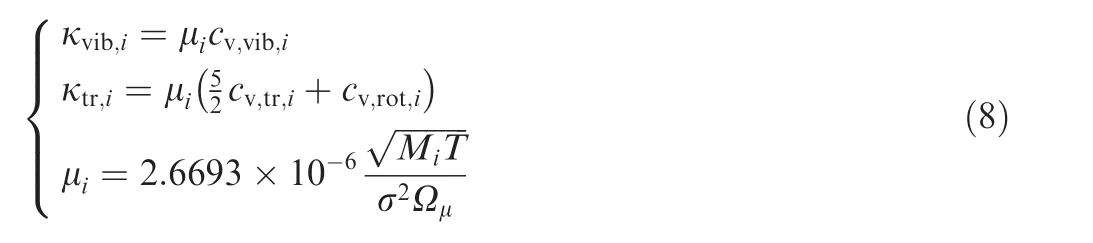
where σ is the characteristic molecular diameter and Ωμis the viscosity collision integral.

Dalton's law was utilized to determine the mixture pressure of gases,which is given as:

where R is the gas constant and Miis the molar weight of the ith species.As the form of pressure,the connections of variables between mixture and individual species are given as:

The sensible enthalpy per unit of mass for species i is defined as:

where cp,iis the heat capacity at constant pressure,evib,iand eele,iare vibrational energy and electronic energy per unit mass for species i,respectively.

The internal or vibrational energy source term with the vibrational relaxation time16has the form

The average relaxation time given by the Milikan-White vibrational relaxation theory17can be expressed as:

To calculate the species production rates˙ωiin the governing equations,the finite-rate ratio model is utilized.In general,Nrchemical reactions involving 7 species can be represented as:

where Vijdenotes stoichiometric coefficient for reactant and product i in reaction j,superscript f and b denote forward and backward.

The mass rate of formation of ith species˙ωiis given as:

where Xiis the mole fraction of the species i,and λijis the third body coefficient.

The rate constants of the forward reactionare determined by the Arrhenius relationship which also were used in Ref.7,and the backward ratecan be derived from the corresponding equilibrium constant.

where A represents the frequency factor and Eais activation energy.

In this work,the chemical reaction set consists of 48 reactions that involve 7 species.These reactions also can be found in Ref.18.

3.2.Radiation model

3.2.1.Mechanism of radiative transition for gas molecules

For near-space hypersonic vehicles,there are a number of species produced in the high-temperature shock layer,which consists of a mixture of ions,electrons,atoms and molecules.Therefore,complex mechanisms of radiation generated by the electronic states of atoms and molecules exist that can be considered in spectroscopic calculations with a line-by-linemethod.These component radiating systems have atomic bound-bound or bound-free(N and O)transitions,and molecular bands(NO,O2and N2).In existing literature,the main mechanisms of ultraviolet radiation for high-temperature gas in the shock layer are listed in Table 1.

Table 1 Band systems of electronic states of molecules that can be considered in the shock layer from Refs.19,20.

In molecular spectroscopy,A,B,C and D represent excited states,and X is the ground state.Their numeric pre-superscript indicates the molecular multiplicity.The symbol∑and∏are electronic states in axial components of Λ =0 and Λ =1,respectively.The superscripts+and-of∑denote signs of the electronic eigenfunction through a symmetrical plane.The subscripts u and g are even and odd states,and r is the regular multiple state.

3.2.2.Absorption coefficient of electronic excitation

The emission coefficient and the absorption coefficient can characterize physical properties of radiation in hightemperature air,and reflect the ability of the species to absorb and emit photons.They individually depend on pressure,temperature and species of the mixture gas.Based on molecular radiative theory,each transition contributes a discrete line for either vibrational and rotational transitions within molecules or electronic transitions and combinations.Therefore,the line absorption coefficient21is expressed as:

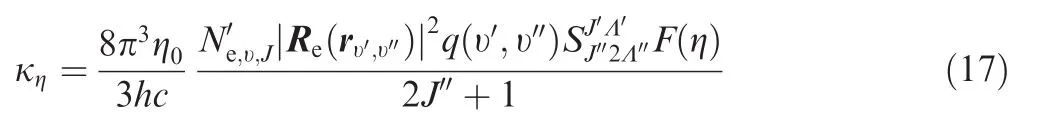
where the single and the double prime represent the upper energy level and the lower energy levelrespectively.|Re(rυ′,υ′)|denotes the matrix element of electronic transition moments,q(υ′,υ′)is the Franck-Condon factor,is the Honl-London factor with rotational degeneracy in the high energy state,is the number density of the molecule in a lower energy level,η0is the center frequency-wave number,and F(η)is a function of the spectral line shape.

For an atom or a molecule,radiation characteristics are only determined by its inherent structure and do not depend on the external temperature.However,for a mixture,the absorption coefficient is associated with the temperature,which influences the population of energy levels.Therefore,computations of the spectral absorption coefficient can be divided into two steps:the radiation calculation forand F(η),and the calculation of number density.The latter is employed to evaluate the number density in lower levels under the thermodynamic state.

If thermal non-equilibrium is to be considered,a threetemperature model,as a function of electronic temperature TE,vibrational temperature TVand rotational-transitional temperature TR,is used to characterize the energy level population and to describe the process of formation and annihilation for excited-state molecules.Thus,three level states of electronic,vibrational and rotational are populated by corresponding Boltzmann distributions as follows22:

where T(e) is the electronic term of the eth electronic level,G(e,υ) is the vibration term of the vth vibrational level,F(e,υ,J) is the rotational term of the Jth rotational level,vth vibrational level and eth electronic level,h is the Planck constant,c is the velocity of light,and geis the degeneracy of the electronic-level of molecules.and Qe

are the molecular partition function,the rotational partition function in the eth electronic level,the vibrational partition function of the Jth rotational,vth vibrational,and eth electronic levels,and the electronic partition function respectively.Based on the prediction of the number density of different levels,the absorption coefficient of the mixture gas species can be obtained by:

where the total coefficient κηis the sum of that for each species κη,iin each transition mechanism.

3.2.3.Radiative transfer calculation of ultraviolet

The UV signature calculation requires solving the RTE by taking into account various emission bands in the source function and particle scattering.Fig.3 shows the sketch of a radiative transfer model where dotted lines denote flow grids.According to the theory of radiative transfer,the monochromatic RTE2describes the variation of the radiance field in a specified direction Ω through a small differential volume and can be given as:

Fig.3 Sketch of the radiative transfer model and LOS method.

where Iλ(s)and Ibλ(s)are spectral radiant intensity and black body spectrum intensity in Ω direction respectively. κaλand κsλare the absorption coefficient and the scattering coefficient of the gas medium with particles.It is noted that the black body spectrum intensity under non-equilibrium conditions should be corrected as given in Refs.21,22,whose values rely on the population of transitions among the upper and lower levels of state.Iλ(s,Ω′)is the spectral scattering intensity in Ω′direction,and Φλ(Ω′,Ω)is the scattering phase function.

For hypersonic flight,neglecting erosion products from the thermal-protective coating,all mixture species will remain in gas phase and particle scattering never occurs in the shock layer.In this case,the radiative transfer equation,introducing optical thickness as τλ= κλL,can be reduced to the following form:

where κλis the spectral absorption coefficient,and L represents the path length.

3.3.Numerical methods

Navier-Stokes equations were solved with a cell-centered finite volume approach,and an implicit scheme was employed to greatly reduce computing time.Based on a structured grid,the approximate equation applicable for a cell can be written as:

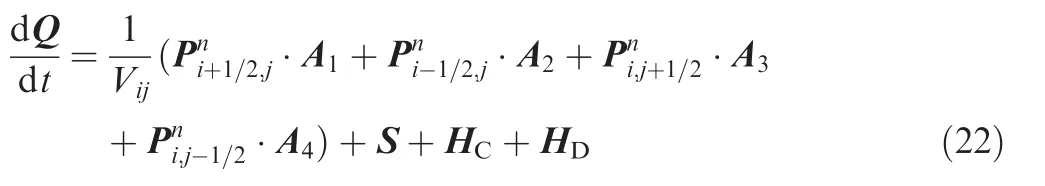
where P=nx(EC+ED)+nr(FC+FD),A1,A2,A3and A4are areas of elemental sides,and nxand nrare axial and radial components of a vector n.The conservative term is placed on the right side of the equation,and on the left side are convective fluxes,source term,and viscous/diffusive fluxes.

In order to improve accuracy in the shock layer,the treatment of convective fluxes used the flux difference scheme,which is equivalent to the Roe approximate Riemann solver based on a second order upwind scheme.23The viscous fluxes,as a function of the gradient and conservative variables velocity and temperature,were discretized using second-order central differencing.The method is described in greater detail in Ref.24.A min-mod limiter borrowed from Ref.25was implemented to control the discontinuous pressure jumps at the shock front.The Runge-Kutta method is utilized here for time stepping.The physical time step is set to 2X10-5s,and each time step has 20 iterations.

The species,temperature and pressure parameters were obtained by the flow field module.The multi-component gas absorption coefficients combined with the multi-temperature model were obtained through line-by-line method.26Spectra with a 5 cm-1resolution were calculated at each grid point along a LOS normal to the body in the forward-viewing window region.A line passing through the shock-layer flow field was calculated in a straightforward manner with a layer-bylayer summation.LOS,when placing a known travel route in the flow,will terminate until the line encounters wall boundaries or departs from the flow field,which is equal to there being no interaction with the lines parallel to the observed direction.This method has been employed in previous work.27Assuming each layered medium is isotropic and isothermal,as shown in Fig.3,the radiative intensity along the LOS can be derived as:

where the superscript i denotes the ith layer,andare directional spectral intensity and black body intensity respectively,andis the transmissivity.Thus,the radiative intensity of a line through the flow covering the wavelengths from λ1to λ2in any direction can be given as:

4.Results and discussion

4.1.Computational approach

To predict the flow field of BSUV,a fine,non-uniform,axisymmetric,orthogonal,instructed grid of 169X158 cells is used with a high resolution near solid boundaries.Fig.4 shows a schematic of the computational domain.A uniform temperature-pressure condition is applied to outer boundaries of the computational domain (a–d).A no-slip,no penetration wall boundary condition (b–c) is imposed on the wall of the dome.An axis symmetric condition (a–b) is employed at the central line of the vehicle.The exit (c–d) has implemented no conditions and is designated as a supersonic outflow boundary.

As mentioned above,the equations solved here are the steady, axisymmetric Reynolds-averaged compressible Navier-Stokes equations with the Menter's shear stress transport (SST) turbulence model,and a binary diffusion model used for closure.Based on the Courant-Friedrichs-Lewy (CFL) number,a local time step is computed with a typical value being 0.1 to improve convergence.Furthermore,the residuals,reduced by at least a factor of 10-6from the starting value,are a necessary condition to properly converge to steady states for all cases.

Fig.4 Sketch for grid distribution.

In this paper,three cases at the 38,53.5 and 71 km altitudes listed in Table 2 are used to validate and analyze present models.Mass fractions of oxygen and nitrogen in ambient atmosphere are 0.23396 and 0.76604 respectively.A mesh sensitivity analysis was carried out in order to estimate the numerical accuracy of the flow field calculation.A comparison of the calculated parameters between a finer 300X300 grid and a basic 169X158 grid is shown in Fig.5.As can be seen,temperature and species mass fractions along the stagnation streamline for two cases are identical.Taking Case 1 as an example,the changes in vibrational temperature,translational temperature,O and NO species are less than 0.1%.Therefore,the basic grid is considered adequate.

4.2.Verification of flow field

High temperature gas heated by the intense ambient atmosphere surrounding hypersonic vehicles displays characteristics of real air.This means that the medium may encompass ionization,radiation,relaxation and non-equilibrium processes.Thus compositional and thermodynamic properties should be a concern in numerical computation.A flight corridor illustration given by Sarma28describes flow regimes and thermochemical phenomena in the stagnation region.According to the flight trajectory of the BSUV experiment,a 7-species reaction scheme is applied for all cases.In Park's multitemperature theory for aerothermodynamics,29the thermal non-equilibrium has an influence on the concentration of species and chemical reaction rates resulting from the difference between translational and vibrational temperatures.Fig.6 illustrates four contours of the translational temperature,the vibrational temperature,and mass fraction of oxygen and nitrogen atoms for Case 2(left)and Case 3(right).This figure demonstrates that the non-equilibrium phenomena become more obvious as the Mach number and altitude increase.This is due to the intensified vibration and ionization that accompanies a rise of temperature around the bow shock.Some differences between contours of Case 2 and Case 3 are also plotted in Fig.7(TTmeans translational temperature).These include higher translational temperatures and longer detached distances for the bow shock,higher vibrational temperature surrounding the forward nose in Case 3,though distribution is similar,and heavier concentration of dissociated species and extensive range.

Fig.5 Grid-independence of the solution.

Table 2 Ambient conditions of BSUV simulations.

Fig.6 Contours of typical parameters for Case 2(left half of contour)and Case 3(right half).

Fig.7 Comparison of translation temperature and vibration temperature.

Fig.8 Comparison of vibration temperature along the stagnation streamline in Case 3.

Fig.9 Number density of NO along the stagnation streamline in Case 1 and Case 3.

To gain confidence with the numerical model used to predict emissions from the shock layer,a validation test is performed on a BSUV blunted cone,and comparison of characteristic parameters is made with the non-equilibrium DSMC method and the multi-temperature CFD model developed by Levin et al.8profiles of the vibrational temperature along the stagnation streamline for Case 3 are given in Fig.8 in which both curves are consistent overall.Fig.9 illustrates number density curves of NO molecules along the stagnation streamline in Case 1 and Case 3.Agreement can be seen between the present model and the CFD method reported by Levin et al.in Case 1.In Case 3,the model's results are located between those of the CFD method and the DSMC procedure.It agrees best with the DSMC in the more heavily concentration regions where higher number density plays an important role in radiation.There are discrepancies for Case 1,however,at positions far from the wall.In the range of 0.6–0.9 normalized distances,the differences can be attributed to a thinner shock layer where high temperatures of gas can be sustained over longer distances than that in Ref.9.Subsequently,the calculated NO stagnation streamline concentration decreases sharply to an extremely small amount and finally to zero.Therefore,it seems unreasonable that Ref.9example remains constant in the end by keeping the temperature of reactions close to ambient temperature.Overall,comparisons of data suggest that the present solution for shock-layer flow is acceptable.

4.3.Validation of absorption coefficient

The non-equilibrium number density can be obtained based on the three-temperature model.Subsequently,the spectra emission coefficient and the absorption coefficient for air mixture can be calculated using the line-by-line method,and validated by shock tube experiments from AVCO Everett Lab.The radiation intensity comparison with R10230and R15631experimentally measured data is given in Fig.10.As plotted in Fig.10(a)and(b),the present data agree well with the experimental data.Consequently,the present radiation calculation module is reliable for predicting the absorption coefficient of the shock layer.

4.4.Validation of ultraviolet intensity

Flow field parameters of the bow shock are treated as input data,and ultraviolet radiation can be predicted by using the radiation model mentioned above.In the current scheme,the three-temperature model is used to obtain the population of the electronic state of species,and the line-by-line technique is employed to evaluate the absorption coefficient of the high temperature multi-species air.The radiation transfer equation is solved with line-of-sight propagation.In the BSUV flight experiments,spectra from the scanning spectrometer(illustrated in Fig.11)show the ultraviolet radiation intensity is mainly determined by nitric oxide gamma(A2∑+)and delta(C2∑+)band systems,and the radiation emitted from(center wavelength is 391 nm)is so weak as to be neglected.9Fig.11 shows a comparison of predictions from the present model with experimental data for ultraviolet radiant intensity.From the plotted UV spectral profiles,there are seven distinct peaks in the ''solar blindquot;region of 200–270 nm,which may be unique spectra features of the bow-shock layer at low altitudes.In addition,radiation from the second excited state to the ground electronic state of the NO molecule delta band system is shown in the center wavelength of 205 nm,and the gamma band system occurs at the peaks of 215,230 and 270 nm.The existence of nitrogen oxide characteristic spectral peaks demonstrates that the dominant radiation is NO.In Fig.11(b),there is an emergence of the OH(X→A)peak at 310 nm above the continuum of the nitrogen oxide band systems for experimental data.This difference near the 310 nm wavelength from Fig.11(a)is because OH signals will be visible with the increase of altitude due to the presence of water in the atmosphere.

Fig.10 Comparison of radiation intensity.

Fig.11 Comparison of the calculated radiant intensity with measured data.

The calculated spectra plotted in Fig.11(a)have a maximum peak absolute magnitude of 4X10-2W/(cm2.μm.sr),which can be compared with 5X10-4W/(cm2.μm.sr)for the spectra shown in Fig.11(b).The difference in intensity of about two orders of magnitude is determined by different flight altitudes.At the same velocity,the molecule-wall collision probability declines as the atmosphere becomes thinner at higher altitudes so that the number density of the excited state molecules is reduced.Spectra profiles predicted by the present model in both Fig.11(a)and(b)are over-predictive compared with the experimental data.At the peak of NO gamma(0,0)(γ(0,0)in Fig.11)of 230 nm and gamma(0,1)of 240 nm,the discrepancy is maximized,up to 50%and 42%respectively.Never the less,error remains below 15%in the ''solar blindquot;region.Note that some uncertainties are unavoidable in radiation calculations for which resolutions of the flow field need to be treated as an input data.In fact,the main sources of error and uncertainty in hypersonic aerothermodynamic modeling consist of physical modeling,spatial/time discretization and ambient conditions.32Taking the free stream as a example,its error can be up to 5%in the 48–69 km altitude range and to 16%in 70–80 km.33Most importantly,the UV emission spectra of the bow-shock layer calculated by the present radiation model show good qualitative agreement with the BSUV flight experiment results in terms of the typical structure and level of intensity.

4.5.Analysis of the bow-shock ultraviolet emission

Agreement between calculations and experimental data for ultraviolet emission intensity within the wavelengths of 200–400 nm is achieved in the four parts of this study.As in the BSUV experiments about sensors,simulations are carried out for viewing ultraviolet radiation intensity from different angles.Fig.12 profiles the comparison of spectra radiation at viewing angles of 0°,15°,30°and 60°for Case 1.The viewing angle is defined as the intersection angle between the centerline of the vehicle and the line of sight.The predicted solutions are observed to have quite a similar distribution,and the intensity declines as the angle increases.The intensity at a viewing angle of 0°is about one order of magnitude higher than that at 30°and about two orders of magnitude greater than that at 60°.

Fig.12 Spherical radiant intensity at different angles for Case 1.

As shown in BSUV experiments using four photometers,the emission features of NO identified were in 215±3 nm and 230±25.5 nm.The photometers were used to select the spectral features of interest.Taking Case 1 as an example,Fig.13 shows that variations in intensity of the spectrum integral relate to viewing angles from 0°to 60°in three bands:212–218 nm,230–280 nm and 200–260 nm.Note that the radiance in each spectral band plotted in Fig.13 decreases with an increase of viewing angle.The intensities in the direction of stagnation streamline at a 0 viewing angle and are heavier than those at the other angles.In the above three bands,the calculated values at a viewing angle of 0°are about two orders of magnitude higher than those at an angle of 60°.In addition,the predicted results in intensity in the band of 230–280 nm are approximately equal to the 200–260 nm band,which indicates the spectrum integral value in band 200–230 nm is roughly equivalent to that in band 260–280 nm.These can depend on spectral intensity and bandwidth.The intensity in band 212–218 nm at each viewing angles is lower by an order of magnitude than the other two bands.The distributions for Case 2 and Case 3 are similar to those plotted in Fig.13,therefore,these profiles are not illustrated.

Fig.14 plots three profiles illustrating radiation characteristics for all cases.The spectra intensity as a function of wavelength is calculated at a viewing angle of 0°to observe emissions toward the stagnation streamline.The intensity in Case 1,similar to Fig.12,is about two orders of magnitude higher than that in Case 2.There are several clear peaks in the region from 200 to about 275 nm,as also shown in Fig.11.For the wavelengths larger than 240 nm,the overall curves of intensity trend downward in all cases.This is especially evident in Case 3,where the ultraviolet spectra emitted from NO bands is extremely weak and displays a steep drop in the short wavelength region of 300–400 nm,which demonstrates that structure and level of spectra profiles differ greatly from those in Case 1 and Case 2.From Fig.14(a),comparisons of three curves show that the intensity in Case 1 is about two orders of magnitude higher than that in Case 2,and the atmosphere of the former,at an altitude of 38 km,is denser than the latter at 53.5 km.Note that the curve in Case 3 remains higher than that in Case 2 and the n becomes lower from 275 nm.One of the most probable reasons for such a difference is a highertemperature region in the shock layer and a lower density ambient gas at 5.1 km/s velocity and 71.0 km altitude for Case 3.As mentioned in Section 3.2,the spectrum emitted from NO(A→X)gamma band is mainly dominated by the two factors of temperature and NO number density.Therefore,the difference between these factors in Case 2 and Case 3 results in variations in intensity relative to position from the stagnation point.

Fig.13 Radiant intensities of characteristic bands at the forward viewing angles for Case 1.

Fig.14 Comparison of radiance predicted.

The column charts in the bottom left corner of the illustrations(from Fig.14(a)–(c))give the radiant intensity in three bands.As can been seen,the values of the intensity from high to low are in bands of 200–260,230–280,and 212–218 nm.For all cases,the total intensity in each band decreases with the increase of viewing angle.The intensity decreases by over an order of magnitude with each additional 30°in viewing angle for Case 1,as well as at a viewing angle of 60°for both Case 2 and Case 3.However,for the latter two cases,there is not much difference in intensity at viewing angles of 0°and 30°due to similar levels of temperature and number density of NO.Meanwhile,the intersection points of the two curves in Fig.14(b)–(c)are located at the wavelengths of 275 nm and 305 nm respectively.Hence the total intensity of band 230–280 nm in Case 3 is higher than that in Case 2.

5.Conclusions

A thermo-chemical non-equilibrium radiation model was developed to predict the ultraviolet emissions in the shock layer for near-space hypersonic vehicles.In this construct,a two-temperature non-equilibrium model and a 7-species,48-reaction chemistry scheme were employed to predict the flow field properties of the shock layer with the finite volume technique.A three-temperature line-by-line method was utilized to evaluate parameters of radiation characteristics for equilibrium and non-equilibrium air,and the RTE was integrated with the LOS method.Comparisons of the results calculated by each module with previous work show the y are in adequate agreement with experimental data.Focusing on the BSUV flights as the object of this research,three cases of 38,53.5 and 71 km altitudes were selected to be systematically compared with previous literature.The ultraviolet spectra predicted by the present computational model demonstrate an identical structure to the measured data.Moreover,the level of intensity,though over-predicted by about 50%in a few narrow regions,agrees well with measurements.The maximum discrepancy occurs at a peak of 230 nm and NO gamma(0,1)(γ(0,1)in Fig.11),but the error remains below 15%in other''solar blindquot;regions.

Simulations were carried out for radiation intensity with different viewing angles as well.From spectra profiles,a seven-peak structure of ultraviolet spectra exists in the ''solar blindquot;region of 200–270 nm,a high density region in the range of NO gamma,delta and beta band systems.The peak absolute magnitude of the intensity was up to 10-2in units of W/(cm2.μm.sr)at a velocity of 3.5 km/s and an altitude of 38 km,while the y dropped to 10-4W/(cm2.μm.sr)at 3.5 km/s and 53.5 km.In the same flight case,the predicted spectra had quite a similar distribution at different viewing angles,but the intensity significantly declined as the viewing angle increased.In relatively thin atmosphere,the structure of spectra emitted from the bow shock may have great changes,and the level drops steeply as well.In summary,this computational model can be used to analyze the ultraviolet spectra features of the shock layer for near-space hypersonic vehicles and will be extended to the infrared spectral band.Within speeds of up to 5.1 km/s and altitudes less than 71.0 km,this model can be used to carry out quantitative analyses of radiative noise for hypersonic vehicles in terms of spectra,bands and viewing angles.

Acknowledgement

This study was supported by the National Natural Science Foundation of China(No.51176039).

1.Levin DA,Candler GV,Limbaugh CC.Multispectral shock-layer radiance from a hypersonic slender body.J Thermophys Heat Transfer 2000;14(2):237–43.

2.Roblin A,Baudoux PE,Chervet P.UV missile-plume signature model.In:Wendlell RW,Dieter C,William RR,editors.AeroSense of international society for optics and photonics;2002 April 1,Orlando,Florida,USA.Washington,D.C.:SPIE;2002.p.344–55.

3.Schreiber P,Dang T,Pickenpaugh T,Smith GA,Gehred P,Litton CW.Solar-blind UV region and UV detector development objectives.Optoelectronics' 99-integrated optoelectronic devices of international society for optics and photonics;1999 Jan 23,San Jose,California,USA.Washington,D.C.:SPIE;1999.p.230–48.

4.Horvath TJ,Cagle MF,Grinstead JH,Gibson DM.Remote observations of reentering spacecraft including the space shuttle orbiter Aerospace conference;2013 March 2–9;Virginia Hampton,USA.Piscataway (NJ):IEEE Press;2013.p.1–15.

5.Erdman PW,Zipf EC,Espy P,Howlett C,Levin DA,Loda R,et al.Flight measurements of low-velocity bow shock ultraviolet radiation.J Thermophys Heat Transfer 1993;7(1):37–41.

6.Erdman PW,Zipf EC,Espy P,Howlett CL,Levin DA,Collins RJ,et al.Measurements of ultraviolet radiation from a 5 km/s bow shock.J Thermophys Heat Transfer 1994;8(3):441–6.

7.Levin DA,Candler GV,Collins RJ,Erdman PW,Zipf E,Espy P,et al.Comparison of theory with experiment for the bow shock ultraviolet rocket flight.J Thermophys Heat Transfer 1993;7(1):30–6.

8.Candler GV,Boyd ID,Levin DA,Moreau S,Erdman P.Continuum and DSMC analysis of bow shock flight experiments.Reston:AIAA;1993.Report No.:AIAA-1993-0275.

9.Levin DA,Candler GV,Collins RJ,Erdman PW,Zipf EC,Howlett CL.Examination of theory for bow shock ultraviolet rocket experiments.I.J Thermophys Heat Transfer 1994;8(3):447–52.

10.Levin DA,Braunstein M,Candler GV,Collins RJ,Smith GP.Examination of theory for bow shock ultraviolet rocket experiments.II.J Thermophys Heat Transfer 1994;8(3):453–9.

11.Levin DA,Collins RJ,Candler GV,Wright MJ,Erdman PW.Examination of OH ultraviolet radiation from shock-heated air.J Thermophys Heat Transfer 1996;10(2):200–8.

12.Boyd ID,Phillips WD,Levin DA.Prediction of ultraviolet radiation in nonequilibrium hypersonic bow-shock waves.J Thermophys Heat Transfer 1998;12(1):38–44.

13.Johnston CO.Nonequilibrium shock-layer radiative heating for Earth and Titan entry[dissertation].Virginia:Virginia Polytechnic Institute and State University;2006.

14.Bird GA.Molecular gas dynamics.Oxford:Clarendon;1976.p.145–67.

15.Vincenti WG,Kruger CH.Introduction to physical gas dynamics.New York:John Wileyamp;Sons,Inc.;1965.p.21.

16.Zhao X,Lei J,Zhang SJ.Hypersonic non-equilibrium computations for ionizing air.Reston:AIAA;2009.Report No.:AIAA-2009-1591.

17.Millikan RC,White DR.Systematics of vibrational relaxation.J Chem Phys 1963;39(12):3209–13.

18.Park C.Review of chemical-kinetic problems offuture NASA missions.I-Earth entries.J Thermophys Heat Transfer 1993;7(3):385–98.

19.Gorshkov AB.The simulation of ultraviolet radiation under conditions of re-entry of space vehicle from near-Earth orbit.High Temp 2010;48(1):12–22.

20.Bose D,Mccorkle E,Thompson C.Analysis and model validation of shock layer radiation in air.Reston:AIAA;2008.Report No.:AIAA-2008-1246.

21.Dong SK,Tan HP,He ZH,Yu QZ.Calculation of spectral absorption coefficient of high temperature equilibrium or nonequilibrium 11-species air.Chin J Aeronaut 2001;14(3):140–6.

22.Dong SK,Ma Y,Tan HP.Modeling of high-temperature air species nonequilibrium spectral radiation properties.J Thermophys Heat Transfer 2008;22(2):301–6.

23.Hirsch C.Numerical computation of internal and external flow.New York:John Wileyamp;Sons,Inc.;1990.p.536–56.

24.Shan J,Surzhikov S,Yan H.Hypersonic nonequilibrium flow simulation based on kinetic models.Front Aerosp Eng 2012;1(1):1–12.

25.Josuyla E,Gaitonde D,Shang JS.Hypersonic non-equilibrium flow computations using the Roe flux-difference split scheme.AIAA J 1993;31(5):812–3.

26.Ozawa T,Garrison MB,Levin DA.Accurate molecular and soot infrared radiation model for high-temperature flows.J Thermophys Heat Transfer 2007;21(1):19–27.

27.Mu L,Ma Y,He ZH,Dong SK.Radiation characteristic simulation of non-equilibrium flow field around the hypersonic blunted cone.J Eng Thermophys 2012;33(11):1958–62.

28.Sarma G.Physico-chemical modelling in hypersonic flow simulation.Prog Aerosp Sci 2000;36(3):281–349.

29.Park C. Nonequilibrium hypersonic aerothermodynamics.Canada:John Wileyamp;Sons,Inc.;1989.p.145–69.

30.Allen R,Camm J,Keck JC.Radiation from hot nitrogen.J Quant Spectrosc Radiat Transfer 1961;1(3):269–72.

31.Allen RA,Camm JC,Rose MH,Rose PH.Nonequilibrium and equilibrium radiation at supersatellite re-entry velocities.Geophysics. Washington, D.C.: NASA; 1963. Report No.:19630018570.

32.Tang ZG,Zhang YY,Chen JQ,Mao ML,Zhang YF,Liu YH.More fidelity,more accurate,more efficient-progress on numerical simulations for hypersonic flow.Acta Aeronaut Astronaut Sin 2015;36(1):120–34(Chinese).

33.Champion K.Middle atmosphere density data and comparison with models.Adv Space Res 1990;10(6):17–26.

Niu Qinglinis a Ph.D.candidate at the School of Energy Science and Engineering,Harbin Institute of Technology(HIT).He received his M.S.degree from Beijing Institute of Technology(BIT)in 2014.His areas of research include rocket exhaust plumes and hypersonic vehicle phenomenology.

He Zhihongis an associate professor at the School of Energy Science and Engineering,Harbin Institute of Technology(HIT),China.She received her M.S.and Ph.D.degrees from the same university.Her main research interests are multi-dimensional radiative transfer and coupled heat transfer and its application to space technology.

Dong Shikuiis a professor and Ph.D.supervisor at the School of Energy Science and Engineering,Harbin Institute of Technology(HIT),China.He received his M.S.and Ph.D.degrees from the same university in 2002.His current research interests are thermal protection of aero-engines,and IR,ultraviolet,amp;polarization imaging.

23 October 2015;revised 16 February 2016;accepted 23 March 2016

Available online 27 August 2016

Bow shock ultraviolent (BSUV);

Hypersonic vehicle;

Shock layer;

Thermal non-equilibrium;

Ultraviolet radiation

©2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 451 68412108.

E-mail address:dongsk@hit.edu.cn(S.Dong).

Peer review under responsibility of Editorial Committee of CJA.