系统误差下基于双重模糊拓扑的编队航迹精细关联算法

王海鹏，潘新龙，贾舒宜，丛瑜

(海军航空工程学院 信息融合研究所，山东，烟台 264001)



系统误差下基于双重模糊拓扑的编队航迹精细关联算法

王海鹏，潘新龙，贾舒宜，丛瑜

(海军航空工程学院 信息融合研究所，山东，烟台 264001)

为解决系统误差下编队内各目标航迹精细关联的难题，基于编队目标航迹的特点，利用模糊拓扑的思想，提出了一种系统误差下基于双重模糊拓扑的编队航迹精细关联算法. 算法首先基于循环阈值模型对各传感器获得的航迹进行编队识别，然后利用编队中心航迹代替编队整体，深入分析系统误差对编队中心航迹的影响，建立第一重模糊拓扑模型，完成编队航迹的预互联和普通目标航迹的对准关联，最后基于预关联编队内目标航迹之间或与航迹关联对之间的拓扑关系建立第二重模糊拓扑模型，实现编队内目标航迹的精细关联. 经仿真数据验证，与基于目标不变信息量的模糊航迹对准关联算法、基于航迹迭代的航迹对准关联算法和修正的加权法相比，该算法综合性能明显优越，能很好满足工程上对系统误差下编队内目标航迹精细关联的需求.

编队航迹；精细关联；系统误差；模糊拓扑

近年来，随着传感器分辨率的提高，编队目标[1-4]跟踪技术受到国内外学者的广泛关注. 在一些实际应用中，与编队的整体态势相比，往往更关心编队内个体目标的情况[2-3]. 例如，当面对敌方编队飞机突防时，为更好地进行战术拦截和打击，要求在探测系统只能部分分辨飞机编队的条件下，尽可能精确估计出编队中飞机的个数及各架飞机的运动轨迹，以便为后续的作战决策提供精确的信息支持. 此时，为有效改善编队内目标的精确跟踪效果，工程上通常利用多套不同的设备、从不同测向获取编队目标测量数据，进行数据互联和融合等处理；因组网传感器通常存在系统误差，系统误差下编队内目标的航迹精细关联成为必须要解决的问题.

然而，传统的系统误差下航迹关联算法[5-16]对编队内目标航迹的复杂性估计不足，设计相对简单，整体关联效果十分有限. 首先，编队中各目标空间距离较小且行为模型相似；如采用系统误差下的模糊航迹关联算法[9，14]，其模糊因素集中的航向、航速等因子已丧失对关联判决的辅助作用，继续采用会干扰正确的模糊评判，加大航迹错误关联率；如采用基于复数域拓扑描述的航迹对准关联算法[15]，其航迹粗关联波门交叉严重，关联信息矩阵的拆分易引起计算爆炸，难以满足系统的实时性要求；如采用基于整体图像匹配的航迹对准关联算法[12-13，16]，其估计旋转和平移量的时间会延长，且当量测误差较大时，其估计值可能发散，不能实现航迹的实时准确关联. 其次，各航迹前后时刻相似性很强，错误的航迹关联在后续时刻会继续存在，此时采用传统的双门限准则进行关联对的确认，会增大错误航迹关联率.

因此，为解决该问题，本文基于编队内目标航迹的特点，利用模糊拓扑的思想，提出了一种系统误差下基于双重模糊拓扑的编队航迹精细关联(formation targets track refined correlation algorithm with systematic error based on double fussy topology，FTTRC-SE-DFT)算法；并建立了多种典型的仿真环境，验证了本文算法的有效性.

1 FTTRC-SE-DFT算法

1.1 基于循环阈值模型的编队识别

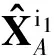
1.2 第一重模糊拓扑关联模型

为实现各传感器重叠探测区域内所有航迹的关联，利用一个等效航迹代替编队整体，建立第一重模糊拓扑关联模型，实现编队整体及普通目标航迹的整体关联.

1.2.1 编队等效航迹的选取

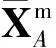
(1)

(2)

1.2.2 系统误差对编队中心航迹的影响分析

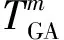
(3)

因为系统误差不改变编队内各目标间的拓扑关系，所以通常情况下rA≈rB，将其代入式(3)得

(4)

同理可得

(5)

总之，系统误差使编队中心航迹发生了整体的旋转和平移，旋转角度与普通目标的旋转角度相同，平移距离由式(4)(5)确定.

1.2.3 模糊拓扑关联模型

基于系统误差对编队中心航迹的影响分析，就编队中心航迹和普通目标构成的整体目标空间而言，各目标间的拓扑关系发生了一定程度的放射变化.

① 模糊因素集的建立.

(6)

式中Td为待关联航迹.

② 模糊因素权值的分配.

(7)

式中a1max和a1min为a1(k)可取的最大值和最小值；rmax为编队中各相邻目标间距离的最大值，可根据技侦情报和目标场景获得. 因此，A1(k)中的各个因子为

(8)

(9)

③ 模糊航迹关联准则的建立.

此处选取正态模糊隶属度函数，建立模糊关联矩阵，结合航迹质量及多义性处理实现编队整体及普通目标的关联，具体过程同文献[16]，在此不再赘述. 但在此需要注意的是，编队航迹的预互联不是最终的关联结果，只是完成编队内航迹精细互联的基础.

1.3 第二重模糊拓扑关联模型

1.3.1 模糊因素集的建立

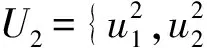
1.3.2 模糊因素权值的分配

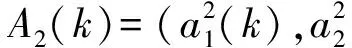
1.3.3 编队内航迹精细关联准则

编队内航迹的精细关联准则与第一重模糊拓扑模型相同，在此不再重复介绍. 需要注意的是，基于编队内航迹的精心关联，可直接利用文献[10]中提出的系统误差下目标状态估计算法，实现分布式多传感器编队内目标的精细跟踪.

2 仿真验证与分析

为验证说明算法性能和有效性，本节采用100次蒙特卡洛仿真，对本文所提出的FTTRC-SE-DFT算法与修正的加权法、基于目标不变信息量的模糊航迹对准关联算法[16](表示为模糊对准算法)及基于航迹迭代的航迹对准关联算法[16](表示为航迹迭代算法)的性能进行仿真比较与分析.

2.1 仿真环境

假定传感器为2部2D雷达，位置分别为(0 m，0 m)，(150 000 m，0 m)，测向误差均为σθ=0.5°，测距误差均为σr=80 m，采样周期均为1 s；为比较各算法在不同仿真环境中的航迹起始性能，设置以下5种典型环境：

① 环境1：模拟常见系统误差稀疏编队目标环境. 稀疏编队目标中各目标的距离一般处于区间(600 m，1 000 m)中. 设在一两维平面上存在14个目标，构成3个匀速直线运动的编队目标；第1个编队由前4个目标组成，初始位置分别为(5 000 m，800 m)，(5 400 m，1 400 m)，(5 850 m，1 500 m)，(6 100 m，900 m)，初始速度均为(0 m/s，-300 m/s)；第2个编队第5～8个目标组成，初始位置分别为(-5 000 m，10 000 m)，(-5 200 m，9 400 m)，(-4 900 m，8 600 m)，(-5 300 m，8 000 m)，初始速度均为(200 m/s，-300 m/s)；第3个编队由剩余目标组成，初始位置分别为(10 000 m，-8 000 m)，(9 500 m，-9 000 m)，(9 000 m，-9 000 m)，(8 500 m，-8 000 m)，(8 000 m，-8 000 m)，(7 500 m，-7 000 m)，初始速度为(-240 m/s，-230 m/s). 两传感器测距系统误差均为0.5 km，测角系统误差分别为0.5°和-0.5°.

② 环境2：模拟常见系统误差密集编队目标环境. 密集编队目标环境编队中各目标的距离一般处于区间(100 m，300 m)中，第1个编队中各目标的初始位置变为(5 000 m，800 m)，(5 200 m，850 m)，(5 350 m，900 m)，(5 550 m，830 m)；第2个编队中各目标的初始位置变为(-5 000 m，10 000 m)，(-5 100 m，9 800 m)，(-5 000 m，9 650 m)，(-5 050 m，9 500 m)；第3个编队中各目标的初始位置变为(10 000 m，-8 000 m)，(9 800 m，-8 000 m)， (9 700 m，-8 200 m)，(9 500 m，-8 300 m)，(9 400 m，-8 400 m)，(9 300 m，-8 300 m)，其他参数同环境1；

③ 环境3：模拟较大系统误差稀疏编队目标环境；目标设定同环境1；两传感器测距系统误差均为1 km，测角系统误差分别为1°和-1°.

④ 环境4：模拟较大系统误差密集编队目标环境；目标设定同环境2；两传感器测距系统误差均为1 km，测角系统误差分别为1°和-1°.

⑤ 环境5：模拟常见系统误差编队目标部分可分辨环境，假设两部传感器分别对第1个编队、第2个编队是部分可辨的；其他参数设置同环境1.

2.2 仿真结果及分析

① 由表1可知，对本文设定的5种环境而言，FTTRC-SE-DFT算法的正确关联概率均为最高，航迹迭代算法次之，模糊对准算法和修正的加权法基本无法对编队内目标航迹进行正确关联. 而且，无论在哪种环境下，FTTRC-SE-DFT算法的正确关联概率均在82%以上，特别是在环境5下，航迹迭代算法的正确关联率已跌至16.86%，而FTTRC-SE-DFT算法的正确关联概率仍高达84.57%，提高了67.71%. 各项指标充分说明了FTTRC-SE-DFT算法具有更为广泛的适用环境，在各种环境中均能对编队内目标航迹进行精确互联，其关联性能远远优于其他3种算法.

② 表2给出了5种环境中各算法的单次仿真耗时. 相比较而言，在各种仿真场景中，航迹迭代算法的实时性能相对最好，模糊对准算法相对最差，修正的加权法和FTTRC-SE-DFT算法居中，且前者略优于后者.

表1 各算法航迹关联概率比较表

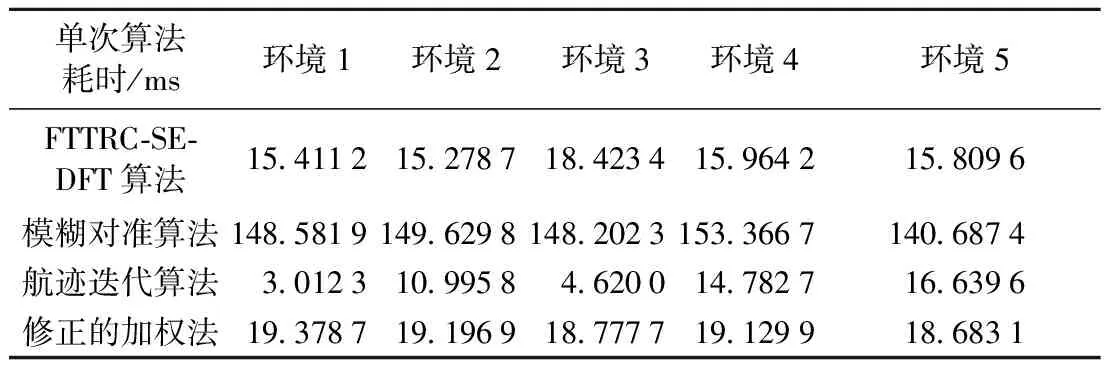
表2 各算法单次耗时比较表

此外，通过比较同一算法在不同仿真环境中的单次耗时可知，FTTRC-SE-DFT算法、模糊对准算法、修正加权法的关联耗时基本不受编队内目标密集程度、系统误差大小以及是否部分可辨等环境因素的影响；而航迹迭代算法的耗时受环境影响较为明显，但其算法实时性亦为最好.

3 结 论

为解决系统误差下编队内目标航迹的精细航迹关联问题，本文提出了一种FTTRC-SE-DFT算法，该算法建立第一重模糊拓扑关联模型，实现编队航迹和普通目标航迹的整体关联；基于参照关联对，建立第二重模糊拓扑关联模型，实现各传感器对编队目标探测状态不一致等复杂环境下的编队内航迹精细关联，且耗时较少、性能稳定，较好地满足了实际工程需求.

[1] 邢凤勇，熊伟，王海鹏.基于聚类和Hough变换的多编队航迹起始算法[J].海军航空工程学院学报，2010，25(6):624-629.

Xing Fengyong， Xiong Wei， Wang Haipeng. Dense multi-formation track initiation algorithm based on k-means clustering and Hough transform[J]. Journal of Naval Aeronautical and Astronautical University， 2010，25(6):624-629. (in Chinese)

[2] Peng Z H， Sun L， Chen J. Path planning of multiple uavs low-altitude penetration based on improved multi-agent coevolutionary algorithm[C]∥Proceedings of 2011 the 30th Chinese Control Conference. [S.l.]: IEEE， 2011:4056-4061.

[3] Zhen Q， Shelton C R. Improving multi-target tracking via social grouping[C]∥Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE， 2012:1972-1978．

[4] 赵盟盟，张群，陈怡君，等.一种用于空间群目标分辨的滑动窗轨迹跟踪算法[J].宇航学报，2015，36(10):1187-1194．

Zhao Mengmeng， Zhang Qun， Chen Yijun， et al. A sliding window tracking algorithm for distinguishing space group targets[J]. Journal of Astronautics， 2015，36(10):1187-1194. (in Chinese)

[5] Xu E， Ding Z， Dasgupta S. Target tracking and mobile sensor navigation in wireless sensor networks[J]. Mobile Computing， 2013，12(1):177-186．

[6] Vo B N， Vo B T， Phung D. Labeled random finite sets and the Bayes multi-target tracking filter[J]. IEEE Transactions on Signal Processing， 2014，62(24):6554-6567.

[7] Bocca M， Kaltiokallio O， Patwari N， et al. Multiple target tracking with RF sensor networks[J]. Mobile Computing， 2014，13(8):1787-1800.

[8] Demigha O， Hidouci W K， Ahmed T. On energy efficiency in collaborative target tracking in wireless sensor network: a review[J]. Communications Surveys & Tutorials， 2013，15(3):1210-1222.

[9] 宋长贺，李云松，宁纪锋，等.分布场的多特征融合目标跟踪方法[J].西安电子科技大学学报，2015，42(4):1-7.

Song Changhe， Li Yunsong， Ning Jifeng， et al. Study of multi-feature fusion methods for distribution fields in object tracking[J]. Journal of Xidian University， 2015，42(4):1-7. (in Chinese)

[10] 崔亚奇，宋强，何友.系统偏差情况下的目标跟踪技术[J].仪器仪表学报，2010，31(8):1848-1854．

Cui Yaqi， Song Qiang， He You. Direct tracking technique when systematic error exist[J]. Chinese Journal of Scientific Instrument， 2010，31(8):1848-1854. (in Chinese)

[11] 许婉君，侯志强，余旺盛，等.背景加权的多特征融合目标跟踪算法[J].空军工程大学学报:自然科学版，2015，16(3):71-76．

Xu Wanjun， Hou Zhiqiang， Yu Wangsheng， et al. Fusing multi-feature object tracking algorithm based on background-weighting[J]. Journal of Air Force Engineering University :Natural Science ed， 2015，16(3):71-76. (in Chinese)

[12] 白浩，赵凯，王越，等.基于K-中心点聚类的模糊航迹关联算法[J].计算机应用，2015，35(A01):310-312．

Bai Hao， Zhao Kai， Wang Yue， et al. Fuzzy track association algorithm based on K-center clustering[J]. Journal of Computer Applications， 2015，35(A01):310-312. (in Chinese)

[13] 何友，宋强，熊伟.基于相位相关的目标航迹对准关联技术[J].电子学报，2010(12)：2718-2723．

He You， Song Qiang， Xiong Wei. Track alignment-correlation technique based on phase correlation[J]. Acta Electronica Sinica， 2010(12)：2718-2723. (in Chinese)

[14] 丁锋，薛磊.基于模糊理论的证据航迹关联算法分析[J].计算机应用研究，2015，32(6):1694-1697.

Ding Feng， Xue Lei. Analysis of track association based on fuzzy evidence theory[J]. Application Research of Computers， 2015，32(6):1694-1697. (in Chinese)

[15] 宋强，熊伟，何友.基于复数域拓扑描述的航迹对准关联算法[J].宇航学报，2011，32(3)：560-566．

Song Qiang， Xiong Wei， He You. A track alignment-correlation algorithm based on topological description of complex number field[J]. Journal of Astronautics， 2011，32(3)：560-566. (in Chinese)

[16] 宋强.目标航迹对准关联与传感器系统误差估计算法研究[D].烟台:海军航空工程学院，2011．

Song Qiang. Target track alignment correlation and sensor system error estimation algorithm[D]. Yantai: Naval Aeronautical and Astronautical University， 2011. (in Chinese)

(责任编辑：李兵)

Formation Targets Track Refined Correlation Algorithm with Systematic Error Based on Double Fussy Topology

WANG Hai-peng，PAN Xin-long，JIA Shu-yi，CONG Yu

(Research Institute of Information Fusion， Naval Aeronautical and Astronautical University，Yantai， Shandong 264001， China)

Aiming to solve the track refined correlation problem of the formation targets with systematic errors， based on the characteristics of the formation tracks and fussy topology theory， an algorithm of track refined correlation within formation targets based on double fussy topology was proposed considering systematic errors. In this algorithm， the formation identification of each sensor was obtained based on the cyclic threshold model firstly. And then the formation center was used to replace the whole formation， the first fussy topology model was established by deeply analyzing the effect of system error on the track of formation center， that is to say the pre-interconnection of formation tracks and alignment of common target tracks were completed. At last， the second fussy topology model was established by the topological relations between the pre-interconnection of formation tracks and correlated tracks， in order to realize formation targets track refined correlation. The analysis results of the simulation data show that the general performance of this algorithm， which can meet the engineering requirement of the track refined correlation of the group targets with systematic errors very well， is better than that of fuzzy track alignment-correlation algorithm based on target invariant information， track alignment-correlation algorithm based on iterative closest track and modified weighted track correlation algorithm.

formation track; refined correlation; systematic error; fussy topology

2016-06-23

国家自然科学基金项目资助项目(61531020，61471383)；国家部委预研基金资助项目(9140A07030514JB14001，9140A07041415JB14001)

王海鹏(1985—)，男，博士，讲师，E-mail：whp5691@163.com.

潘新龙(1983—)，男，博士生，E-mail：airadar@126.com.

TP 953

A

1001-0645(2016)09-0960-06

10.15918/j.tbit1001-0645.2016.09.015