基于ANSYS的管笼结构抗震分析

贾守亚+肖广涛

摘 要：运用有限元分析软件ANSYS对管笼参数化建模，通过模态分析确定管笼的固有频率，根据设备的固有频率的计算结果，确定x、y、z三个方向的地震加速度，通过计算确定设备各部位的受力情况。计算结果对管笼的结构设计有实际意义，明确放映出管笼结构在地震状况下的结构安全性。

关键词：ANSYS；抗震分析；管笼结构

中图分类号：TH122；TP391 文献标识码：A 文章编号：1006-8937（2016）27-0160-02

1 概 述

管笼结构是在化工领域广泛使用的设备，管笼的种类繁多、形式多样，但其基本结构是类似的，多由主管道、法兰、阀门及其支座组成。管笼结构在工程应用中必须具有足够的强度，否则不能保证安全运行。在实际运用中，管笼结构主要受到地震载荷的破坏，需要对其在地震作用下的强度进行校核。

本文利用ANSYS对某工程的管笼参数化建模，通过计算确定设备各部位的受力情况。Ansys软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件。它能与大多数CAD软件接口，实现数据的共享和交换，是现代产品设计中的高级CAE工具之一。所以选择Ansys软件对管笼结构进行有限元分析，能够准确的反应管笼机构在地震载荷下各部分的受力状况。

2 计算方法

本文以管笼结构为例，首先通过利用Ansys有限元分析软件对其进行参数化建模，其次通过模态分析确定设备的频率，然后通过频率的计算结果，确定设备在x、y、z三个方向的地震加速度，最后通过力学分析对设备进行抗震计算[1]。

3 有限元模型的建立

3.1 模型简化

实物分析模型，如图1所示，简化模型，如图2所示。

本次分析在有限元建模时对Pipe Cage设备三维模型进行了简化，具体如下：

将主管道内的cooling water简化为质点单元并均布于内壁；

将阀门及组件内部的冷却水简化为质点单元，质点位置位于简化部分的重心，且作用于对应的法兰连接位置；

连接螺栓或铆钉采用具有等径和材质的beam单元简化，忽略了影响网格划分的圆角、倒角、小孔等小特征，焊接简化为绑定接触。将阀门及部分组件简化为质点单元后，其在结构上的连接关系使用MPC单元来模拟[2]；

简化后有限元模型总质量为5 155 kg。

3.2 网络划分说明

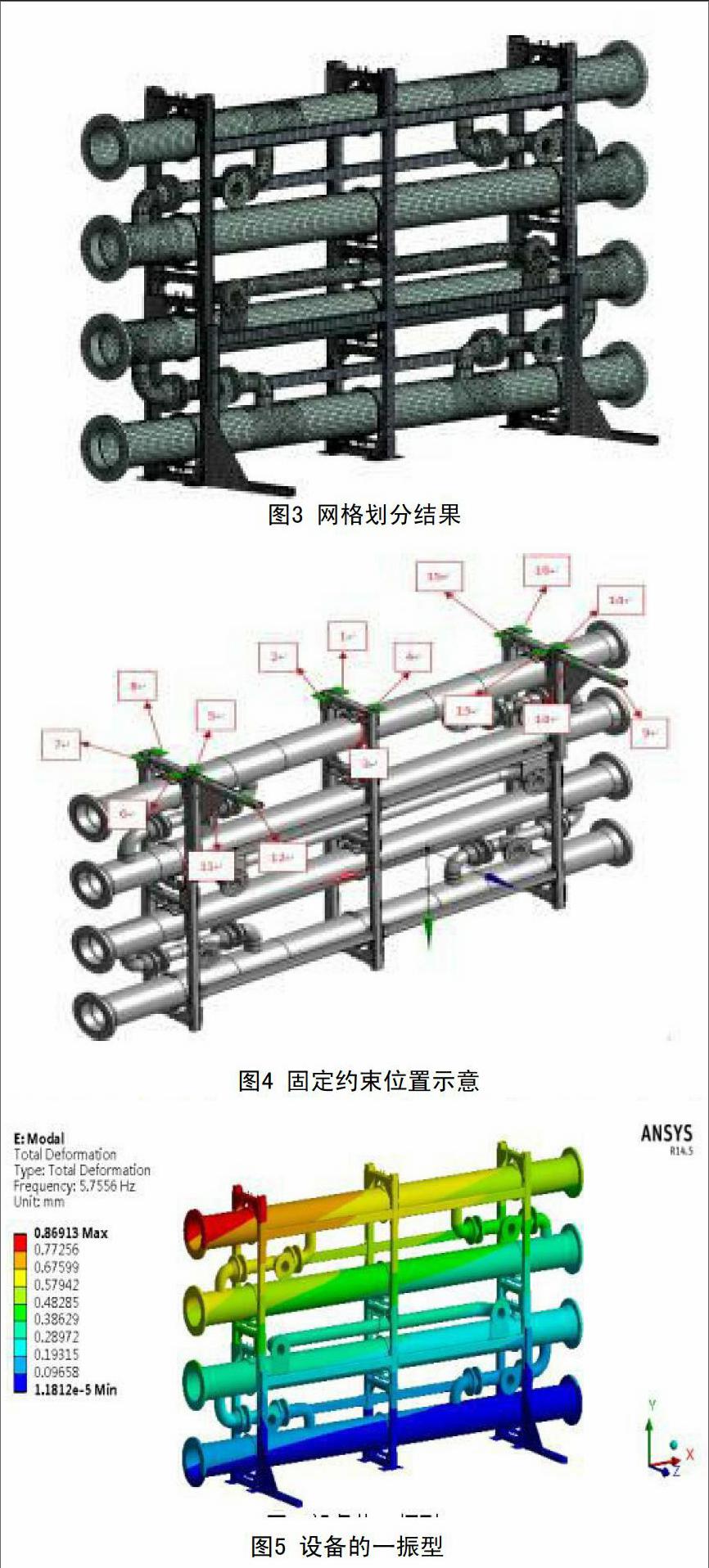
本次分析对框架结构主体主要使用20节点三维六面体单元solid186进行网格划分，对管道采用solid285四面体单元进行网格划分，主要体网格尺寸设置为8～20 mm。共生成159 888个单元，528 770个节点。网格划分结果，如图3所示。

3.3 分析方法

本次谱分析使用SRSS振型组合法叠加，模态分析约束的位置见图4所示，地震加速度方向按照系统坐标系X、Y、Z三个方向分别进行计算[3]。

模态分析约束支点使用的碳素结构钢螺栓ASTM A36弹性模量为MPa，泊松比为0.26，材料密度为7 850 kg/m3，螺栓的屈服强度为250 MPa，抗拉强度为500 MPa。

3.4 模态分析

由于管笼结构在地震载荷的作用下，其变形与内力均与设备的自振周期和振型有关，因此模态分析是对管笼结构进行抗震计算的基础。对支座上16个螺栓进行全自由度约束，施加载荷并求解，可获得设备的固有频率，地震载荷只考虑模型的一阶基本振型与固有频率的影响，一阶振型，如图5所示，可以看出一阶固有频率为5.7 Hz。

4 计算结果

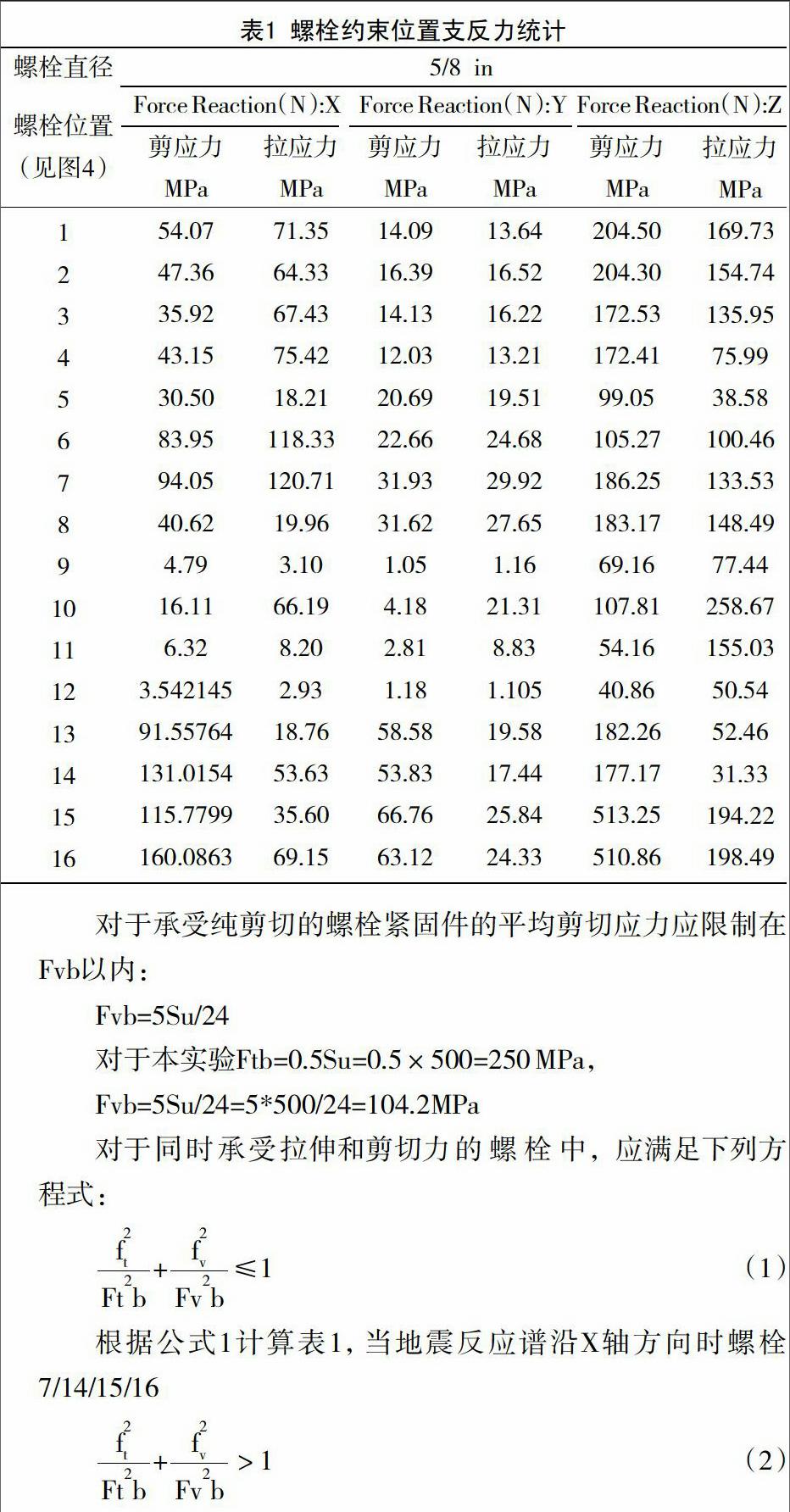
当地震反应谱分别沿x、y、z时，螺栓约束位置支反力统计，见表1。

4.1 地震反应谱沿X轴方向时

当地震反应谱沿X轴方向时，螺栓约束位置支反力统计，见表1。

因此当地震反应谱沿X轴方向时螺栓7、14、15、16存在失效的可能。

4.2 地震反应谱沿Y轴方向时

当地震反应谱沿X轴方向时，螺栓约束位置至反力统计，见表1。根据公式1对表1中各螺栓的约束支反力计算可知，所有螺栓均满足公式1，因此当地震反应谱沿Y轴方向时，所有螺栓均能满足抗震要求。

4.3 地震反应谱沿Z轴方向时

当地震反应谱沿X轴方向时，螺栓约束位置至反力统计见表1。根据公式1对表1中各螺栓的约束支反力计算可知，仅螺栓5/9/11/12能满足公式1，能满足抗震要求。

因此当地震反应谱沿Z轴方向时，设备发生大面积失效。

5 结 语

当地震反应谱沿X轴方向时，螺栓7、14、15、16存在失效的可能。

当地震反应谱沿Y轴方向时，所有螺栓均能满足抗震要求。

当地震反应谱沿Z轴方向时，设备发生大面积失效。

从计算结果可以看出，该设备不满足抗震要求，建议通过改变设备结构，选用高力学性能的材料来满足抗震要求。

参考文献：

[1] 余伟炜，高炳军，陈洪军.ANSYS在机械与化工装备中的应用2版[M].北 京：中国水利水电出版社，2007.

[2] 陈淑玲，陈帆，林利芬.基于ANSYS的减速器斜齿-直齿圆柱齿轮的模 态分析[J].企业技术开发，2012，（31），6-8.

[3] 任辉启.ANSYS7.0工程分析实例讲解[M].北京：人民邮电出版社， 2003.