SM2椭圆曲线公钥加密算法的研究与实现

李玉生

（南京理工大学 自动化学院，江苏 南京 210094）

SM2椭圆曲线公钥加密算法的研究与实现

李玉生

（南京理工大学 自动化学院，江苏 南京 210094）

随着互联网的发展，越来越多的信息交换通过网络进行，在这些信息中包含着不能为人所知的私密信息，例如，信用卡账号、银行账号、病历、电子邮件等。由于私密信息泄露产生不良后果的事件时有发生，这些都牵扯到对数据信息的加密问题。针对这一问题，文章提出运用SM2加密算法实现数据信息的加密，保证网络通信的安全性。事实表明，SM2公钥加密算法能够更加安全地加密数据信息，且加密的数据很难破译。

私密信息泄露；SM2加密算法；安全性；难破译

保密通信催生了密码技术，从古到今先进的技术都首先应用在军事领域，军队历来是使用密码最频繁的地方，保护己方秘密洞悉敌方秘密是克敌制胜的重要条件，正所谓“知己知彼，百战不殆”，古代中国所使用的密码技术主要有：阴符、阴书、虎符、信牌、字验和矾书等。西方的传统密码技术主要包含凯撒密码、换字式密码、多表替代密码、转制式密码等。第二次世界大战密码学得到了长远的发展，无论是在密码学的技术、理论，还是在应用方面，都发生了革命性的变化。

1976年，公钥密码算法的思想被提出，1978年，第一个公钥密码算法RSA诞生了，标志着密码学进入了一个全新的时代。2010年国家密码管理局提出了SM2椭圆曲线公钥密码算法主要包括数字签名算法、密钥交换协议和公钥加密算法3部分。

本论文主要研究SM2公钥加密算法并基于keil uVision 5软件平台采用C语言编程，将设计的模加、模减、模乘、模幂和模逆5个底层运算函数封装成库函数，供点加、倍点、标量乘函数和其他模块调用，最后，在LPC1778硬件平台上实现数据的加密与解密。

1　公钥加密算法简介

公钥加密算法又称非对称加密算法，相对于只有一个密钥的对称加密算法，非对称加密算法中加密密钥和解密密钥是一对密钥，可以由解密密钥通过一定的数学算法计算出加密密钥，而加密密钥理论上即使知道了数学算法也很难推导出解密密钥，这就是密钥在数学上的大数难解问题。由于加密密钥是公开的，理论上任何人都可以获得这个加密密钥用来加密信息，但是使用加密密钥加密的消息只有相应的解密密钥可以解开，而这个解密密钥是保密的，是不公开的。非对称密码算法中，加密密钥也叫作公开密钥或公钥，解密密钥则称为私人密钥或私钥。

例如，通信双方A和B建立通信，公钥密码算法实现的是A和B之间的数据加密，加解密过程如图1所示。

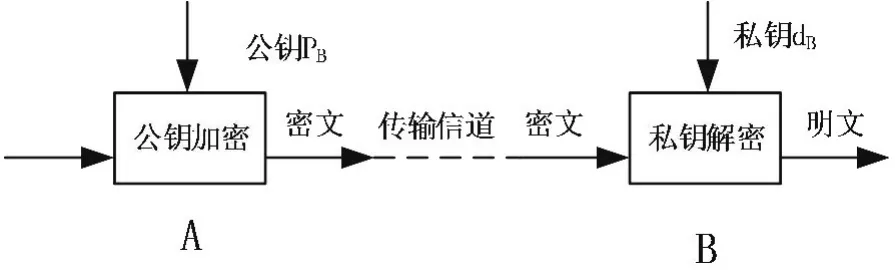
图1　公钥加密算法的加密和解密过程

A要发送消息给B，那么A必须持有B的公钥作用于明文进行加密将加密后的密文发送给接收方B，B在接收到密文后，用自己持有的私钥作用于密文进行解密操作，还原出A发送的明文。同样B要发送数据给A则用自己的私钥加密明文将生成的密文发送给接收方A，接收方A用B的公钥解密收到的密文就能还原出B发送的明文了，但是这样不能保证数据传输的私密性。因为B的公钥是公开的所以理论上获得B的公钥的人，都可以解密出明文信息，要实现B向A发送密文数据，则B应该持有A的公钥，用A的公钥加密数据把密文发送给A，A用自己的私钥解密密文获得明文信息，也就是说A和B之间相互的通信需要A的公钥、私钥，B的公钥、私钥共4把钥匙，A 和B各持有对方的公钥，私钥只有A和B自己知道。

在这一过程中要保证私钥的私密性，这样即使密文被人截获了，在没有私钥的情况下也无法破译出密文所对应的明文信息，仅私钥的持有者能够解密密文获取明文信息，保证了信息的安全性。公钥密码算法的公钥和密码算法是公开的。原则上，B的公钥人人都可以获取，所以数据加密不提供身份认证和不可抵赖的功能。关于身份认证的内容，即A如何确定收到的公钥是B的，可由SM2椭圆曲线公钥密码算法的数字签名算法保证。

由于对称密码算法加密解密使用的是同一把钥匙，密钥在传递的过程中容易遭到窃取，导致密钥泄露，使用公钥密码算法加密数据的一大好处是通信双方不需要事先协商加密密钥，减少了密钥泄露的风险，也扩大了通信对象的范围，所有人都可以使用公钥密码算法轻易地建立安全的通信信道。

2　椭圆曲线大数运算的数学基础

2.1模运算与素数域

同余是数论中的等价关系，对于正整数m如果有a=b+km （a，b，k均是整数）那么记b=a mod（m），则称a与b关于m同余。当m=p（p为素数）时，我们定义素数域FP可由{0，1，2，3…p-1}中P个元素构成，关于P的模运算称为素数域上模运算。

2.2有限域上的模运算的设计与实现

有限域上的模运算是SM2椭圆曲线公钥密码算法的基础，主要包括模加和模减运算、模乘运算、模幂和模逆运算。

模逆运算是模运算中最复杂运算量最大的运算，模逆运算可以通过费马小定理（n是素数的时候，和n互素的某个整数a有公式an-1=1modn成立）得到，即当p为素数时，有ap-1=1mod p，则可得到模逆运算a-1=ap-2mod p，这样就可以利用模幂运算来表示模逆运算。以上的这些模运算都已在LPC1778硬件平台上实现，如图2所示。

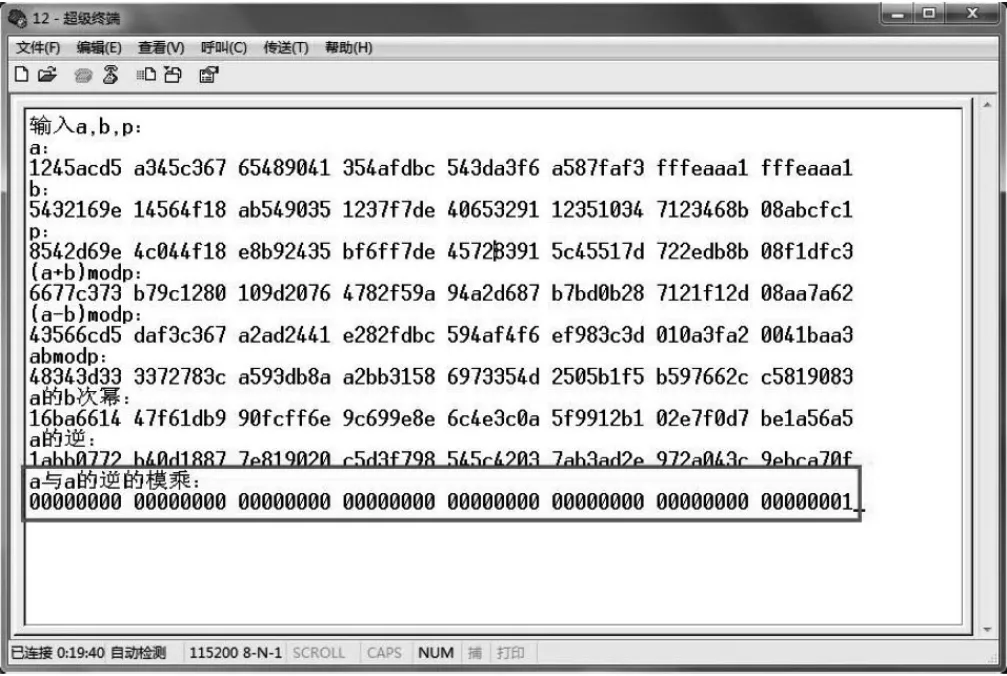
图2　模运算测试结果

2.3有限域上标量乘运算的设计与实现

标量乘的数学形式，P=（xp，yp）为椭圆曲线E（FP）上的点，k为正整数，P的k倍点为Q。Q=［k］P=P+P+…+P（k 个p）。标量乘运算是所有运算中最耗时的运算操作，主要由点加和倍点产生，点加和倍点运算在不同坐标系下的运算规则不同。采用仿射与雅可比混合坐标系下的运算规则：y2=x3+axz4+bz6，其中，a，b为椭圆曲线上的整数，并且△= （4a3+27b2）mod p≠0。

三维坐标P（x1，y1，z1），Q（x2，y2，1）的无穷远点为（1，1，0）。倍点运算P+P=（ x3，y3，z3）声明为Padd1（x1，y1，z1，x3，y3，z3），把2P的值存入（x3，y3，z3），点加运算P+Q=（x3，y3，z3）声明为Padd2（x1，y1，z1，x2，y2，x3，y3，z3），把P+Q的值存入（x3，y3，z3）。最后还要把结果（x3，y3，z3）从雅可比加重摄影坐标系下转换到仿射坐标系下，需要对参数进行转换：x3=x3/ z12，y3=y3/z13，即可得到所需的二维坐标点（x3，y3）。

有了点加和倍点运算就可以进行标量乘运算，标量乘从右往左的算法为：

3　SM2公钥加密算法

素数域椭圆曲线的参数：素数域的模P，椭圆曲线E（FP）的系数：a，b；E（FP）上的基点G（Gx，Gy）≠0，基点G的解为n余因子h=1，用户A持有的用户B的公钥PB，用户B持有的私钥dB。

3.1SM2加密算法

（1）用随机数发生器生成随机数k，0＜k＜n。

（2）计算椭圆曲线上的点C1=［k］G。

（3）计算椭圆曲线点S=［h］PB，若S为无穷远点则报错并退出，h为余因子，这里取为1。

（4）计算椭圆曲线上的点［k］PB=（x2，y2）。

（5）计算t=KDF（x2||y2，len）若t全为0则返回1。

（6）计算C2=M⊕t。

（7）计算C3= SM3（x2||M||y2）。

（8）计算密文C=C1||C2||C3。

SM2加密流程如图3示。

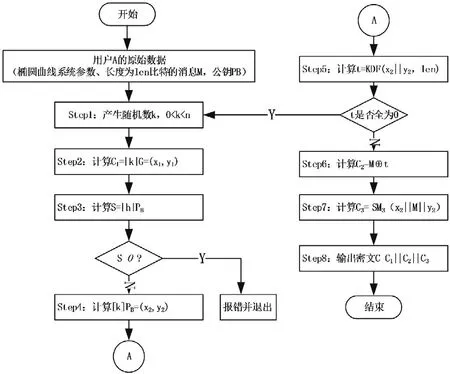
图3　SM2加密算法流程

3.2SM2解密算法

（1）从密文中取出C1，验证C1是否满足椭圆曲线方程，若不满足则报错并退出。

（2）计算S=［h］C1，若S为无穷远点则报错并退出。

（3）计算 ［dB］C1=（x2，y2）。

（4）计算 t=KDF（x2||y2，len）。

（5）从C中取出C2计算m= C2⊕t。

（6）计算u=SM3（x2||m||y2），若u与C3不相等，则报错并退出。

（7）输出明文m。

SM2解密流程如图4所示。

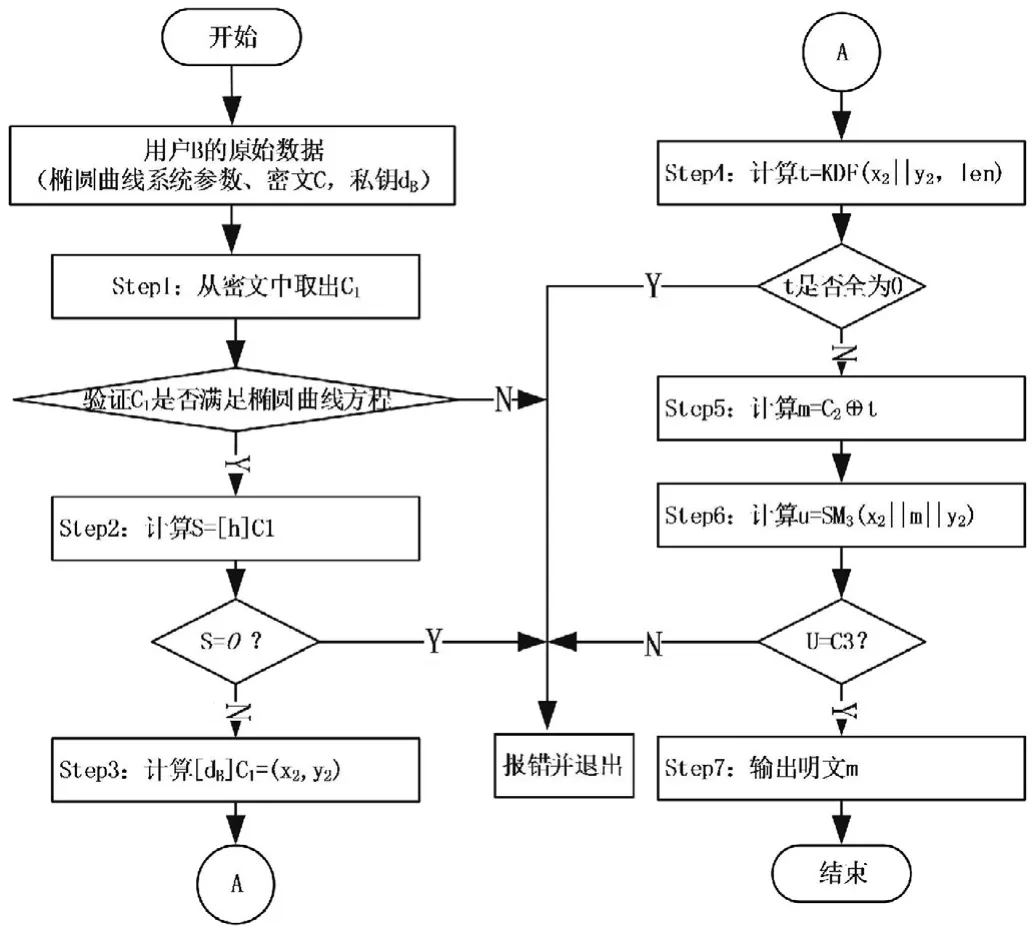
图4　SM2解密算法流程

加密解密算法在LPC1778上实现通过串口RS232在超级终端上的显示结果如图5所示，待加密的消息M为“Hello World！”。

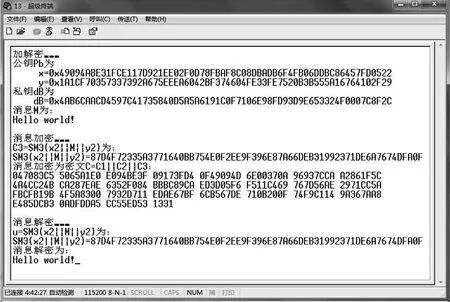
图5　加解密测试结果

4　结语

SM2公钥加密算法可以实现数据的加密，但相对于对称密码算法如DES，AES等对称密码算法计算量大，加密速度慢，所以在实际应用中一般把公钥密码算法和对称密码算法结合起来使用，既利用了公钥密码算法的密钥易于传输的优点又利用了对称密码算法加密速度快、适合大批量数据加密的优点。

[1]张明德，刘伟.PKI/CA与数字证书技术大全[M].北京：电子工业出版社，2015.

[2]卢开澄，卢华明.椭圆曲线密码算法导引[M].北京：清华大学出版社，2008.

[3]刘合义.谈数论中的同余及其应用[J].计算机学报，2004（1）：38-39.

[4]李学俊，敬忠良.基于椭圆曲线离散对数问题的公钥密码[J].计算机工程与应用，2002（6）：20-22.

[5]周宣武，杨晓元，黄德官，等.网络中基于椭圆曲线密码的密钥管理方案[J].计算机工程，2004（11）：89-91.

[6]国家密码管理局.SM2椭圆曲线公钥密码算法[EB/OL].（2016-10-25）[2010-12-18].http://wenku.baidu.com/view/6337c57c27284b73f242501a. html.

[7]刘铎，戴一奇.计算椭圆曲线上标量乘的快速算法[J].计算机学报，2008（3）：102-106.

[8]李辉，刘中华，易军凯.基于伪随机数生成器的标量乘改进算法[J].计算机系统应用，2015（1）：151-155.

[9]牛广平，马建峰.椭圆曲线标量乘的快速实现[J].计算机工程，2004（16）：45-46.

[10]LAUTER K.The Advantages of Elliptic Curve Cryptography for Wireless Security.[J]Wireless Communications，2004（3）：62-67.

[11]NEAL K，ALFRED M，VANSTONE S.The State of Elliptic Curve Cryptography Designs[J].Codes and Cryptography，2010（1）：173-193.

Research and realization of SM2 elliptic curve public key encryption algorithm

Li Yusheng
（Automation School of Nanjing University of Science and Technology, Nanjing 210094,China）

With the development of the Internet, more and more information is exchanged through the network, among those information, there are some private information that can not be known by others, for example, credit card accounts, bank accounts, medical record, e-mail, etc. Bad consequences caused by private information leakage occurred frequently, which is involved in the encryption of data information. In view of this problem, this paper proposes the use of SM2 encryption algorithm to achieve data encryption and ensure the security of network communication. Facts show that the SM2 public key encryption algorithm can encrypt data more safely, and the encryption data is difficult to decipher.

private information leakage; SM2 encryption algorithm; security; difficult to decipher

李玉生（1989— ），男，江苏徐州，硕士研究生；研究方向：arm嵌入式软件开发，SM2公钥密码算法。