Assessment of surface drag coefficient parametrizations based on observations and simulations using the Weather Research and Forecasting model

LI Fu-Ning， SONG Jin-Bo， HE Hi-Lun， LI Shung， Li Xin GUAN Shou-De

aInstitute of Oceanology， Chinese Academy of Sciences， Qingdao， China；bCollege of Earth Science， University of Chinese Academy of Sciences，Beijing， China；cOcean College， Zhejiang University， Zhoushan， China；dState Key Laboratory of Satellite Ocean Environment Dynamics， Second Institute of Oceanography， Hangzhou， China；eInstitute of Atmospheric Physics， Chinese Academy of Sciences， Beijing， China

Assessment of surface drag coefficient parametrizations based on observations and simulations using the Weather Research and Forecasting model

LI Fu-Ninga，b， SONG Jin-Baoc， HE Hai-Lund， LI Shuangc， Li Xiab，eand GUAN Shou-Dea

aInstitute of Oceanology， Chinese Academy of Sciences， Qingdao， China；bCollege of Earth Science， University of Chinese Academy of Sciences，Beijing， China；cOcean College， Zhejiang University， Zhoushan， China；dState Key Laboratory of Satellite Ocean Environment Dynamics， Second Institute of Oceanography， Hangzhou， China；eInstitute of Atmospheric Physics， Chinese Academy of Sciences， Beijing， China

The drag coefcient is important in meteorological studies of the boundary layer because it describes the air-sea momentum fux. Eight drag coefcient schemes were assessed. These parametrizations were compared taking into account data from in situ and laboratory observations. The drag coefcients determined using three schemes were consistent with the level-of phenomenon， supported by the results of laboratory studies. The drag coefcient determined using one scheme decreased at wind speeds higher than approximately 30 m s-1， in agreement with indirect measurements under typhoon conditions. In contrast， the drag coefcients determined using the other four schemes increased with wind speed， even under high wind regimes. Sensitivity tests were performed using simulations of two super typhoons in the Weather Research and Forecasting model. While the typhoon tracks were negligibly sensitive to the parametrization used， the typhoon intensities （the maximum 10-m wind speed and the minimum sea level pressure）， sizes， and structure， were very sensitive to it.

ARTICLE HISTORY

Revised 27 April 2016

Accepted 27 April 2016

Air-sea momentum fux；drag coefcient； typhoon；WRF model

海气界面动量交换对台风发展起着重要作用，其估算公式依赖于拖曳系数。本文利用观测和台风模拟试验对八种拖曳系数参数化方案进行系统的评估。结果表明，相对于早期的参数化方案，近些年提出的参数化方案对拖曳系数的描述有了显著的改进，主要体现在高风速条件下。不同的拖曳系数参数化方案对超强台风“海燕”的模拟路径几乎没有影响，但是对其强度、尺寸和结构的模拟结果有显著影响。

1. Introduction

A bulk formula is often used to represent the exchange of momentum fux （also known as wind stress） between the atmosphere and the ocean surface. The bulk formula is given by

where τ is the air-sea momentum fux， ρ is the density of the air， U10is the 10-m wind speed， and Cdis the drag coeffcient. The extrapolation of Cdderived from feld measurements made in weak wind regimes （assuming that Cdcontinuously increases with wind speed） has been shown not to be robust either in theory （Andreas 2004； Emanuel 2003）， laboratory experiments （Alamaro 2001； Donelan et al. 2004； Troitskaya et al. 2012）， or feld studies （Bell，Montgomery， and Emanuel 2012； Black et al. 2007； Jarosz et al. 2007； Potter et al. 2015； Powell， Vickery， and Reinhold 2003）. It is believed that Cdstops increasing for strong winds（generally with wind speeds greater than 30 m s-1）. Various parametrizations of Cdhave been proposed in recent years，but the parametrizations difer greatly because they have been developed using a variety of methods and datasets. A comprehensive comparison of the parametrizations would therefore be useful for those wishing to use Cdin practice.

The air-sea momentum fux plays a crucial role in the intensifcation and maintenance of a tropical cyclone. Potential intensity theory and the results of numerical models presented by Emanuel （1986， 1995） suggest that the square of the maximum wind speed） and the minimum central pressure （Pmin） of a tropical cyclone in a given environment will be dependent on the ratio of the enthalpy exchange coefcient （Ck） and Cd， and that the Ck/Cdratio in a real typhoon should not be less than 0.75. Other modelling studies （Bryan 2012， 2013； Bryanand Rotunno 2009； Green and Zhang 2013） have produced results that are consistent with the potential intensity theory to some degree， and it has been accepted that Vmax～ （Ck/Cd）1/2. Green and Zhang （2013） conducted fve physical sensitivity experiments using three diferent momentum fux parametrizations and two diferent moist enthalpy fux parametrizations， using version 3.4.1 of the Weather Research and Forecasting （WRF） model. They found that the surface fuxes signifcantly afected a simulation of Hurricane Katrina （2005） and that in particular Cdafected the pressure-wind relationship and the maximum surface wind radius of the hurricane. Recently， it has been shown that Cdcan be optimized using data assimilation（e.g. 4D Variational Data Assimilation）， and some new models can be obtained through data assimilation （Li et al. 2013； Peng and Li 2015； Peng， Li， and Xie 2013）.

In the study， eight previously published Cdparametrizations were compared with each other and with observational data. The sensitivities of simulated typhoons to the diferent parametrizations were then examined using version 3.6 of the WRF model.

The confguration of the WRF model and the experimental design are presented in Section 2. The eight Cdparametrizations are described in Section 3. A comparison and validation of the parametrizations with the observations， as well as analyses of the modelling results for two super typhoons， are provided in Section 4. And fnally， the study is summarized in Section 5.

2. Method

The ‘Advanced Research' core of the WRF model， version 3.6， was utilized to simulate typhoons Haiyan and Maysak using the selected Cdparametrizations. A two-domain confguration with two-way nesting was used in the WRF model. The horizontal grid resolution in the outer domain（D01） was 18 km， and in the inner domain （D02） was 6 km. For the simulation of typhoon Haiyan （2013）， D01 was from 0° to 20°N and 115°E to 155°E， and D02 was from 4°N to 14°N and 120°E to 150°E. For the simulation of typhoon Maysak （2015）， D01 was from 0° to 20°N and 120°E to 170°E，and D02 was from 5°N to 15°N and 134°E to 156°E. The time steps used in D01 and D02 were 60 and 20 s， respectively. There were 44 levels in the vertical direction， and 12 of these levels were inhomogeneous and below 3 km. The model extended up to a height of 50 hPa （approximately 30 km）. The microphysics scheme presented by Lin， Farley，and Orville （1983）， the revised MM5 Monin-Obukhov surface layer scheme （Beljaars 1995； Dyer and Hicks 1970；Paulson 1970； Webb 1970； Zhang and Anthes 1982）， the BouLac planetary boundary layer scheme （Bougeault and Lacarrere 1989）， the Dudhia shortwave scheme （Dudhia 1989）， and the ‘rapid radiative transfer model' longwave scheme （Mlawer et al. 1997） were implemented in both domains. The Kain-Fritsch cumulus scheme （Kain 2004）was used only in D01， and no cumulus parametrization was adopted for D02. A simple mixed-layer ocean model（Pollard， Rhines， and Thompson 1973） was coupled with the atmospheric model to provide updated SSTs.

The initial conditions and lateral boundary conditions in the WRF model were obtained from the NCEP ‘FNL' （fnal）‘operational global analysis' data-set， with a 1° × 1° grid and at intervals of six hours. The wave-age-related parametrization of Cdwas examined using peak-wave-period data with a resolution of 0.5° （from the US Environmental Research Division's Data Access Program； http://oos.soest.hawaii. edu/erddap/griddap/NWW3_Global_Best.html） and providing these to the WRF model every six hours to allow the wave age to be calculated. The peak-wave-period data were taken from the WaveWatch III Global Wave Model，implemented by the University of Hawaii. The wave model was forced using the U.S. NCEP ‘Global Forecast System' wind data， and it was initialized daily， making the peakwave-period data consistent with the initial and lateral boundary conditions of the WRF model.

The experiments were begun at 1800 UTC 4 November 2013 for Typhoon Haiyan and at 1800 UTC 28 March 2015 for Typhoon Maysak， and were integrated for 72 h， covering the development and rapid strengthening stages of the typhoons. The hourly results from D02 were used in the analysis described below.

3. Description of the selected parametrizations

In a neutrally stratifed atmosphere， the surface Cdcan be expressed in terms of the momentum roughness length（z0） as

where the von Karman constant k is taken to be 0.4 and the reference height z is typically 10 m.

The default option for the z0parametrization in the WRF model is based on the Charnock relationship given by

Table 1.The values of Cdfor the diferent parametrizations at moderate （U10= 30 m s-1） and high （U10= 70 m s-1） wind speed.

Figure 1.The relationships between the drag coefcient and the surface wind speed for the wind-speed-related parametrizations（solid lines） and the Liu2012 scheme at diferent wave ages β*（dashed lines）.

with the Charnock coefcient α = 0.0185 （Wu 1980）， where g is acceleration due to gravity and u*is the friction velocity. The second term on the right-hand side of Equation（3） represents the smooth-fow component， supported by viscous shear （Edson et al. 2013）. Charnock1955， TY2001， TYlimit， Moon2007， Davis2008，Andreas2012， Edson2013， and Liu2012 to represent the parametrizations tested. As mentioned above， the formula for z0in the TYlimit scheme was the same as in the TY2001 scheme except that the TYlimit scheme had an upper limit （z0≤ 2.85 × 10-3m）. The specifc values of Cdby the diferent schemes at moderate （U10= 30 m s-1） and high （U10= 70 m s-1） wind speed are presented in Table 1.

The relationships between Cdand the surface wind speed in the parametrizations tested are shown in Figure 1. The value of Cdwas larger and increased at a higher rate in the Edson2013 scheme than in the other wind-speedrelated or friction-velocity-related schemes. Cdincreased rapidly （at almost the same rate） in the Charnock1955 and Davis2008 scheme. The value of Cdin the TY2001 scheme increased at a moderate rate and the Cdbecame smaller than in the Davis2008 scheme at wind speeds of 40 m s-1and higher. The Cdtended to level of and approach roughly 3 × 10-3at high wind speeds in both the Andreas2012 and the Moon2007 scheme. The upper limit of 2.85 × 10-3m on z0caused the Cdin the TYlimit scheme to remain at approximately 2.4 × 10-3at wind speeds higher than 20-30 m s-1. The wave-age-related Liu2012 scheme was distinctly diferent from the other schemes in that Cdreached a maximum at wind speeds of 25-33 m s-1and then decreased linearly as the wind speed increased further. A lower wave age in the Liu2012 scheme corresponded with a higher maximum Cdand weaker surface winds. In the real simulation of Typhoon Haiyan， the wave age was found to decrease quickly as the wind speed increased， causing Cdto increase quickly in weak and moderate winds and then slowly decrease in strong winds （fgures not shown）.

The Cdvalues determined using the eight parametrizations and observational data are also compared in Figure 1. The Cdvalues determined using the Andreas2012，Moon2007， and TYlimit schemes were very close to the Cdvalues obtained from laboratory measurements made by Donelan et al. （2004） and Troitskaya et al. （2012）， particularly at high wind speeds （30-52 m s-1）. The Cdonly decreased at wind speeds higher than 25-33 m s-1in the Liu2012 scheme， and this agreed with feld observations reported by Powell， Vickery， and Reinhold （2003） and Jarosz et al. （2007）. The Liu2012 scheme also partly attributed the scatter in the observed Cddistribution at specifc wind speeds to the diferent wave states during the measurements （Liu， Guan， and Xie 2012）. However， the observations in Figure 1 were obtained in a limited range of wind speed （less than 52 m s-1， roughly）. Bell， Montgomery， and Emanuel （2012） computed drag coefcients obtained from six separate aircraft missions into the major hurricanes of Fabian and Isabel （2003）， at a range of surface wind speeds from 52 to 72 m s-1， but the data showed a large scatter （the values of Cdranged from 0.4 × 10-3to 5.2 × 10-3for wind speeds greater than 52 m s-1）. Thus， it is hard to decide which of the candidate schemes in Figure 1 was the most realistic according to the observations available.

4.2. Simulated results

The WRF model was used to investigate how diferent Cdparametrizations （i.e. the roughness length z0） afected the two simulated super typhoons. Typhoon Haiyan（2013）， which had a maximum wind speed of 87 m s-1，and Typhoon Maysak （2015）， which had a maximum wind speed of 72 m s-1， both formed in the western North Pacifc Ocean. The simulated tracks， maximum 10-m wind speeds，

and minimum SLPs for the typhoons are presented here. Further structural analyses and comparisons are presented only for Typhoon Haiyan because of its extraordinary intensity.

4.2.1. Tracks and intensities

Figure 2.（a） Observed best track of Typhoon Haiyan from the JTWC （thick line） and the simulated tracks determined using the eight parametrizations （thin lines）. （b） The maximum 10-m wind speeds， with lines as defned in （a）. （c） As in （b） but for the minimum SLPs. As for Typhoon Haiyan， the results of Typhoon Maysak are displayed in （d-f）， except that in （f） the observed SLP data are provided by the Regional Specialized Meteorological Center of the Tokyo-Typhoon Center at the Japan Meteorological Agency.

Table 2.RMSEs of the maximum U10and the minimum SLP relative to the observations for the simulated typhoons using diferent Cdparametrizations from 12 to 72 h in 6-h intervals.

There were slight diferences （less than 50 km） between the diferent simulated tracks for the typhoons （as shown in Figure 2（a） and （d））， which could be ignored. Compared with the observed tracks， the simulated tracks for Typhoon Maysak （shown in Figure 2（a）） were much more accurate than those for Typhoon Haiyan （shown in Figure 2（d））. All of the simulated tracks for Typhoon Haiyan were to the right of the best track， and the bias reached almost 2° of latitude after 48 h. However， the simulated tracks for Typhoon Maysak were quite close to the observed track. As shown in Figure 2（b）-（f）， both the maximum U10and the minimum SLP were very sensitive to the parametrization selected. Small values of Cdin the simulations seemed to lead to strong surface winds. For example， the simulation using the Liu2012 scheme gave the highest maximum surface wind speed for both typhoons because it gave the lowest Cdat high wind speeds. However， though the values of Cdwere smaller in the TYlimit and Moon2007 schemes than that in the Andreas2012 scheme at high wind speeds，the maximum surface winds from 48 to 72 h in the simulations of typhoon Maysak were weaker using the TYlimit and Moon2007 schemes than that using the Andreas2012 scheme. There were also some exceptions related to the simulated minimum SLP. For example， the Edson2013 scheme gave a larger Cdbut a lower minimum SLP than most of the other wind-speed-related parametrizations for both typhoons. Compared with the observations， for typhoon Haiyan， the simulation using the Liu2012 scheme gave the lowest RMSEs of the maximum U10and the minimum SLP （as shown in Table 2）， whereas the Davis2008 scheme led the worst simulation. However， for Typhoon Maysak， the RMSE of the maximum U10was almost 3-5 m s-1larger in the simulation using the Liu2012 scheme than using the other schemes， and the Liu2012 scheme also led to a bigger deviation for the SLP than most of the other schemes （except the Moon2007 scheme）.

4.2.2. Size

The radius of the maximum U10（RU10） and the average radius of 35 kts （approximately 17.5 m s-1） winds （R35）were defned as the inner-core and the outer size of Typhoon Haiyan， respectively. The inner-core sizes of the simulations （shown in Figure 3（a）） increased slightly from 35 to 45 km on average between 12 and 72 h. However， in the simulation using the Liu2012 scheme， RU10 decreased slowly up to 50 h， and then increased slowly with time. The outer sizes （shown in Figure 3（b）） increased quickly and linearly from 150 to 325 km （350 km in the simulation using the Davis2008 scheme） between 12 and 54 h，then grew slowly to 350 km by 72 h， which suggests that the simulated typhoons reached a quasi-steady state after 54 h. RU10 and R35 were both lowest in the simulation using the Liu2012 scheme and highest in the simulation using the Davis2008 scheme.

4.2.3. Structure: wind and pressure

The relationships between the minimum surface central pressures and the maximum surface wind speeds for the simulations of Typhoon Haiyan and the results for the JTWC best track are shown in Figure 3（c）. The simulations and observations intersected at roughly 56 m s-1at 940 hPa，above which the wind speeds and pressures were higher in the simulations than the observations， and below which the opposite was true. The simulated points showed considerable scatter at relatively low pressures. The results in the simulation using the Moon2007， TYlimit， Andreas2012，and Liu2012 scheme were much closer to the best track，but only the simulation using the Liu2012 scheme could reproduce the points at wind speeds higher than 80 m s-1. Four radius-height plots of the horizontal， radial， and vertical winds at 67 h are shown in Figure 3（d） as examples， allowing further assessment of the structure of the simulated Typhoon Haiyan. The maximum horizontal wind speeds in the lowest 8 km were more than 95 m s-1in the simulations using the Edson2013， Moon2007，and Liu2012 schemes， but only reached roughly 85 m s-1in the simulation using the Davis2008 scheme. The radii of the maximum horizontal winds were less than 50 km（approximately 40 km） to the right of the center in the simulations using the Edson2013， Moon2007， and Liu2012 schemes， and the Liu2012 scheme also gave a strong wind zone on the left side of the center. However， the radii of the maximum horizontal winds were roughly 60 km on both sides of the center in the simulation using the Davis 2008 scheme. Strong infow and outfow occurred mainly below and above 2 km， respectively. Infow was more obvious to the right of the center， while outfow was dominant on the left. Convergence at low levels caused upward motion near the area at which the maximum horizontal wind speed occurred， and the vertical motion was much weaker in thesimulation using the Moon2007 scheme than in the other simulations.

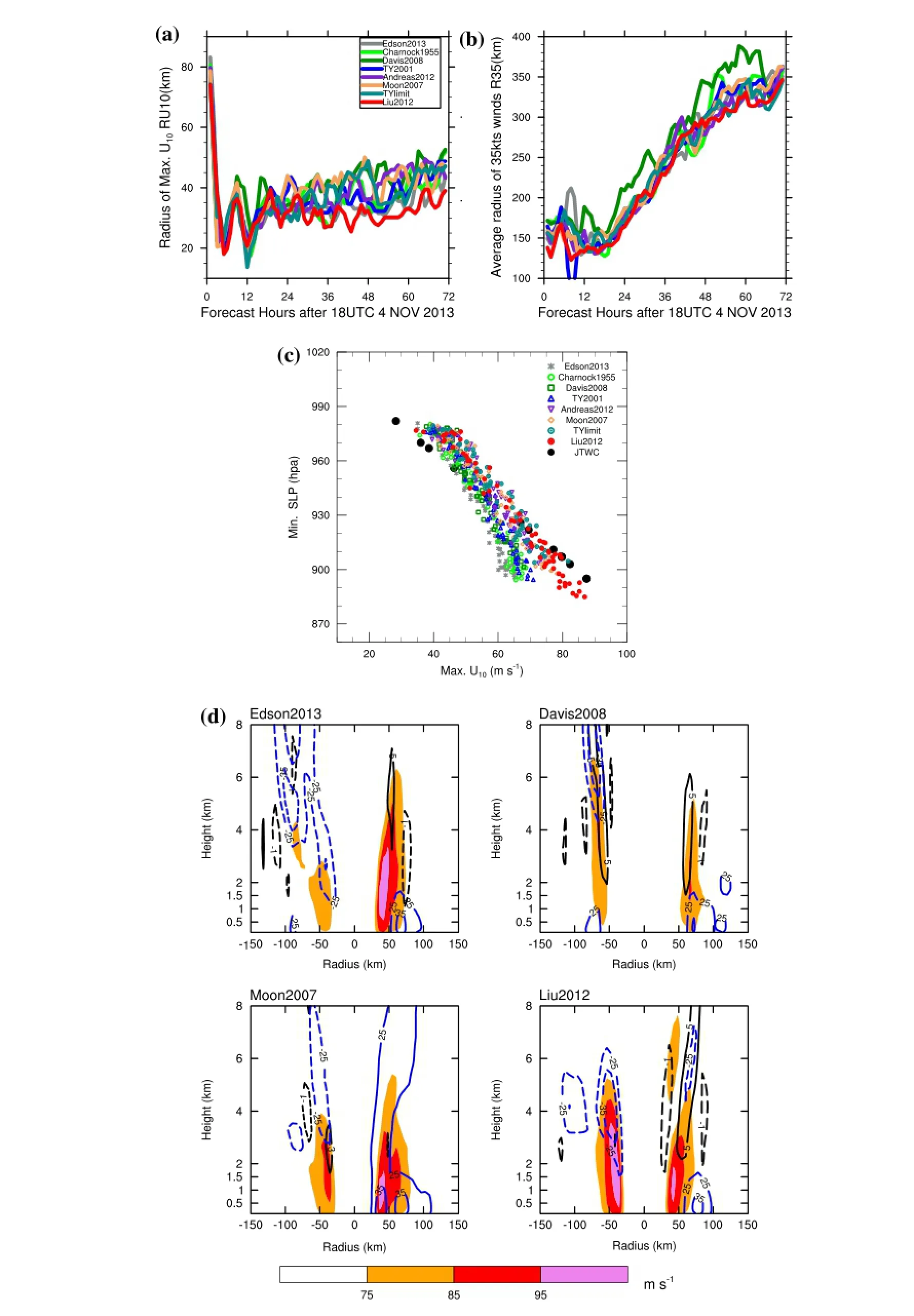
Figure 3.Time series of （a） the radius of the maximum U10（RU10） and （b） the average radius of 35 kts winds （R35） for the simulated Typhoon Haiyan. （c） Scatter plot of the maximum U10and the minimum SLP in the Typhoon Haiyan simulations from 12 to 72 h at intervals of 1 and the JTWC observations from 0 to 72 h at intervals of 6 h. （d） Radius-height plots at 67 h for strong horizontal wind speeds（colored contours）， the radial wind speed （infow （outfow） in solid （dashed） blue）， and the vertical wind speed （upward （downward） in solid （dashed） black） for the Typhoon Haiyan simulations using the Edson2013， Davis2008， Moon2007， and Liu2012 scheme， respectively.

5. Summary

Eight parametrizations of Cdwere comprehensively compared and assessed in this study. It is difcult to observe the behaviour of Cdin strong winds， so some parametrizations of Cd（e.g. Charnock 1955； Davis et al. 2008； Edson et al. 2013） have been extrapolated from feld measurements in weak winds， which all reveal that Cdrapidly increases as the surface wind speed increases. By combining the wave height and wave steepness， the formula proposed by Taylor and Yelland （2001） reduces the rate at which the Cdincreases with wind speed. Laboratory observational datasets （Donelan et al. 2004； Troitskaya et al. 2012） acquired in strong winds tend to cause Cdto be saturated at wind speeds exceeding about 30 m s-1. This feature is approximately described by the formulae proposed by Andreas， Mahrt， and Vickers （2012）and Moon et al. （2007） and the restrained formula proposed by Taylor and Yelland （2001） in the WRF model. A wave-age-related scheme （Liu， Guan， and Xie 2012）was also used in this study， and this gave a decreasing Cdvalue at wind speeds of more than 25-33 m s-1，consistent with feld measurements （Jarosz et al. 2007；Powell， Vickery， and Reinhold 2003）. The observations of Cdwere limited in the region and range of wind speeds，and presented big scatters， and thus more accurate observations at high wind speeds are necessary for validation of the Cdparametrizations.

Numerical simulations of super typhoons Haiyan（2013） and Maysak （2015） were performed using version 3.6 of the WRF model with diferent Cdparametrizations. Large diferences between the eight schemes had almost no infuence on the tracks of the simulated typhoons. The typhoon intensity indicated by the maximum 10-m wind speed and the minimum SLP was very sensitive to the selected parametrization. The size， wind-pressure relationship， and vertical structure of the wind feld for the simulated Typhoon Haiyan were also afected by the surface momentum fux.

The simulations performed in this study serve to raise awareness of how and to what extent the diferent Cdparametrizations can afect simulated typhoons， but do not reveal which parametrization can help produce the most accurate simulation compared with observation. Some other physical or dynamical parametrized processes， the spatial resolution of the WRF model， and the accuracy of initial conditions may also have a signifcant infuence on typhoon modelling. As the next step of this research， more typhoon cases will be simulated using a coupled oceanwave-atmosphere model to give some general results.

Disclosure statement

No potential confict of interest was reported by the authors.

Funding

This research was supported by the National Key Basic Research Program of China （973 Program） ［grant number 2012CB417402］；the Strategic Priority Research Program of the Chinese Academy of Sciences ［grant number XDA11010104］； the National Natural Science Foundation of China ［grant numbers 41576013，41476021， 41506023］； the National High Technology Research and Development Program of China （863 Program） ［grant number 2013AA122803］.

Notes on contributors

LI Fu-Ning is a graduate student at the Institute of Oceanology（IO）， Chinese Academy of Sciences （CAS）. His main research interests are numerical modeling， tropical cyclone， air-sea interaction， and boundary-layer meteorology.

SONG Jin-Bao is a professor at Ocean College， Zhejiang University. His main research interests are non-linear surface waves， internal waves， upper ocean mixing， air-sea fuxes. His recent publications include papers in Boundary-Layer Meteorology， Deep-Sea Research Part I， Acta Oceanologica Sinica，and other journals.

HE Hai-Lun is an associate research scientist at SIO， SOA. His main research interests are tropical cyclone， surface waves， and upper ocean dynamics. His recent publications include papers in Geophysical Research Letters， Acta Oceanologica Sinica， China Ocean Engineering， and other journals.

LI Shuang is an associate professor at Ocean College， Zhejiang University. Her main research interests are air-sea interaction，upper ocean mixing， ocean dynamics and numerical simulation. Her recent publications include papers in Journal of Geophysical Research-Ocean， Acta Oceanologica Sinica， Chinese Physics B， Chinese Journal of Oceanology and Limnology， and other journals.

LI Xia is a graduate student at the Institute of Atmospheric Physics （IAP）， Chinese Academy of Sciences （CAS）. Her main research interests are numerical modeling， coastal ocean dynamics， air-sea interaction and data assimilation.

GUAN Shou-De is a postdoc at the Institute of Oceanology （IO），Chinese Academy of Sciences （CAS）. His main research interests are numerical modeling， upper ocean mixing and tropical cyclone. His recent publications include papers in Journal of Geophysical Research-Ocean， Chinese Journal of Oceanology and Limnology， and other journals.

References

Alamaro， M. 2001. “Wind Wave Tank for Experimental Investigation of Momentum and Enthalpy Transfer from the Ocean Surface at High Wind Speed.” PhD diss.， Massachusetts Institute of Technology.

Andreas， E. L. 2004. “Spray Stress Revisited.” Journal of Physical Oceanography 34: 1429-1440.

Andreas， E. L.， L. Mahrt， and D. Vickers. 2012. “A New Drag Relation for Aerodynamically Rough Flow over the Ocean.”Journal of Atmospheric Sciences 69: 2520-2537.

Beljaars， A. C. M. 1995. “The Parametrization of Surface Fluxes in Large-scale Models under Free Convection.” Quarterly Journal of the Royal Meteorological Society 121: 255-270.

Bell， M. M.， M. T. Montgomery， and K. A. Emanuel. 2012. “Air-Sea Enthalpy and Momentum Exchange at Major Hurricane Wind Speeds Observed during CBLAST.” Journal of Atmospheric Sciences 69: 3197-3222.

Black， P. G.， E. A. D'Asaro， W. M. Drennan， J. R. French， P. P. Niiler，T. B. Sanford， E. J. Terrill， E. J. Walsh， and J. A. Zhang. 2007. “Air-Sea Exchange in Hurricanes: Synthesis of Observations from the Coupled Boundary Layer Air-Sea Transfer Experiment.”Bulletin of the American Meteorological Society 88: 357-374.

Bougeault， P.， and P. Lacarrere. 1989. “Parametrization of Orography-induced Turbulence in a Mesobeta-scale Model.”Monthly Weather Review 117: 1872-1890.

Bryan， G. H. 2012. “Efects of Surface Exchange Coefcients and Turbulence Length Scales on the Intensity and Structure of Numerically Simulated Hurricanes.” Monthly Weather Review 140: 1125-1143.

Bryan， G. H. 2013. “Comments on ‘Sensitivity of Tropical-cyclone Models to the Surface Drag Coefcient'.” Quarterly Journal of the Royal Meteorological Society 139: 1957-1960.

Bryan， G. H.， and R. Rotunno. 2009. “The Maximum Intensity of Tropical Cyclones in Axisymmetric Numerical Model Simulations.” Monthly Weather Review 137: 1770-1789.

Charnock， H. 1955. “Wind Stress on a Water Surface.” Quarterly Journal of the Royal Meteorological Society 81: 639-640.

Davis， C.， W. Wang， S. S. Chen， Y. Chen， K. Corbosiero， M. DeMaria，J. Dudhia， et al. 2008. “Prediction of Landfalling Hurricanes with the Advanced Hurricane WRF Model.” Monthly Weather Review 136: 1990-2005.

Donelan， M. A.， B. K. Haus， N. Reul， W. J. Plant， M. Stiassnie， H. C. Graber， O. B. Brown， and E. S. Saltzman. 2004. “On the Limiting Aerodynamic Roughness of the Ocean in Very Strong Winds.”Geophysical Research Letters 31: L18306. doi:http://dx.doi. org/10.1029/2004GL019460.

Dudhia， J. 1989. “Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-dimensional Model.” Journal of Atmospheric Sciences 46: 3077-3107.

Dyer， A. J.， and B. B. Hicks. 1970. “Flux-gradient Relationships in the Constant Flux Layer.” Quarterly Journal of the Royal Meteorological Society 96: 715-721.

Edson， J. B.， V. Jampana， R. A. Weller， P. S. Bigorre， A. J. Plueddemann， C. W. Fairall， S. D. Miller， L. Mahrt， D. Vickers，and H. Hersbach. 2013. “On the Exchange of Momentum over the Open Ocean.” Journal of Physical Oceanography 43: 1589-1610.

Emanuel， K. A. 1986. “An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-state Maintenance.” Journal of Atmospheric Sciences 43: 585-605.

Emanuel， K. A. 1995. “Sensitivity of Tropical Cyclones to Surface Exchange Coefcients and a Revised Steady-state Model Incorporating Eye Dynamics.” Journal of Atmospheric Sciences 52: 3969-3976.

Emanuel， K. A. 2003. “A Similarity Hypothesis for Air-Sea Exchange at Extreme Wind Speeds.” Journal of Atmospheric Sciences 60: 1420-1428.

Foreman， R. J.， and S. Emeis. 2010. “Revisiting the Defnition of the Drag Coefcient in the Marine Atmospheric Boundary Layer.” Journal of Physical Oceanography 40: 2325-2332.

Green， B. W.， and F. Zhang. 2013. “Impacts of Air-Sea Flux Parametrizations on the Intensity and Structure of Tropical Cyclones.” Monthly Weather Review 141: 2308-2324.

Jarosz， E.， D. A. Mitchell， D. W. Wang， and W. J. Teague. 2007.“Bottom-up Determination of Air-Sea Momentum Exchange under a Major Tropical Cyclone.” Science 315: 1707-1709.

Jones， I. S. F.， and Y. Toba. 2008. Wind Stress over the Ocean. Cambridge: Cambridge University Press.

Kain， J. S. 2004. “The Kain-Fritsch Convective Parameterization: An Update.” Journal of Applied Meteorology and Climatology 43: 170-181.

Li， Y.， S. Peng， J. Yan， and L. Xie. 2013. “On Improving Storm Surge Forecasting Using an Adjoint Optimal Technique.” Ocean Modelling 72: 185-197.

Lin， Y. L.， R. D. Farley， and H. D. Orville. 1983.“Bulk Parameterization of the Snow Field in a Cloud Model.” Journal of Applied Meteorology and Climatology 22: 1065-1092.

Liu， B.， C. Guan， and L. Xie. 2012. “The Wave State and Sea Spray Related Parametrization of Wind Stress Applicable from Low to Extreme Winds.” Journal of Geophysical Research: Oceans （1978-2012） 117: C00J22. doi:http://dx.doi.org/10.1029/2011JC007786. Mlawer， E. J.， S. J. Taubman， P. D. Brown， M. J. Lacono， and S. A. Clough. 1997. “Radiative Transfer for Inhomogeneous Atmospheres: RRTM， a Validated Correlated-K Model for the Longwave.” Journal of Geophysical Research: Atmospheres（1984-2012） 102: 16663-16682.

Moon， I. J.， I. Ginis， T. Hara， and B. Thomas. 2007. “A Physics-based Parameterization of Air-Sea Momentum Flux at High Wind Speeds and Its Impact on Hurricane Intensity Predictions.”Monthly Weather Review 135: 2869-2878.

Paulson， C. A. 1970. “The Mathematical Representation of Wind Speed and Temperature Profles in the Unstable Atmospheric Surface Layer.” Journal of Applied Meteorology and Climatology 9: 857-861.

Peng， S.， and Y. Li. 2015. “A Parabolic Model of Drag Coefcient for Storm Surge Simulation in the South China Sea.” Scientifc Reports 5: 15496. doi:http://dx.doi.org/10.1038/srep15496.

Peng， S.， Y. Li， and L. Xie. 2013. “Adjusting the Wind Stress Drag Coefcient in Storm Surge Forecasting Using an Adjoint Technique.” Journal of Atmospheric and Oceanic Technology 30: 590-608.

Pollard， R. T.， P. B. Rhines， and Rory O. R. Y. Thompson. 1973.“The Deepening of the Wind-mixed Layer.” Geophysical Fluid Dynamics 4: 381-404.

Potter， H.， H. C. Graber， N. J. Williams， C. O. Collins， R. J. Ramos， and W. M. Drennan. 2015. “In Situ Measurements of Momentum Fluxes in Typhoons.” Journal of Atmospheric Sciences 72: 104-118.

Powell， M. D.， P. J. Vickery， and T. A. Reinhold. 2003. “Reduced Drag Coefcient for High Wind Speeds in Tropical Cyclones.”Nature 422: 279-283.

Taylor， P. K.， and M. J. Yelland. 2001. “The Dependence of Sea Surface Roughness on the Height and Steepness of the Waves.” Journal of Physical Oceanography 31: 572-590.

Troitskaya， Y. I.， D. A. Sergeev， A. A. Kandaurov， G. A. Baidakov，M. A. Vdovin， and V. I. Kazakov. 2012. “Laboratory and Theoretical Modelling of Air-Sea Momentum Transfer under Severe Wind Conditions.” Journal of Geophysical Research: Oceans （1978-2012） 117: C00J21. doi:http://dx.doi. org/10.1029/2011JC007778.

Webb， E. K. 1970. “Profle Relationships: The Log-linear Range，and Extension to Strong Stability.” Quarterly Journal of the Royal Meteorological Society 96: 67-90.

Wu， J. 1980. “Wind-stress Coefcients over Sea Surface near Neutral Conditions-A Revisit.” Journal of Physical Oceanography 10: 727-740.

Zhang， D.， and R. A. Anthes. 1982. “A High-resolution Model of the Planetary Boundary Layer-Sensitivity Tests and Comparisons with SESAME-79 Data.” Journal of Applied Meteorology and Climatology 21: 1594-1609.

海气动量通量； 拖曳系数；台风； WRF模式

25 February 2016

CONTACT SONG Jin-Bao songjb@zju.edu.cn

© 2016 The Author（s）. Published by Informa UK Limited， trading as Taylor & Francis Group.

This is an Open Access article distributed under the terms of the Creative Commons Attribution License （http://creativecommons.org/licenses/by/4.0/）， which permits unrestricted use， distribution， and reproduction in any medium， provided the original work is properly cited.