An observational study on vertical raindrop size distributions during stratiform rain in a semiarid plateau climate zone

CHEN Yong， AN Jun-Ling，b， LIU Hui-Zhind DUAN Jing

aState Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry， Institute of Atmospheric Physics， Chinese Academy of Sciences， Beijing， China；bCenter for Excellence in Urban Atmospheric Environment， Institute of Urban Environment， Chinese Academy of Sciences， Xiamen， China；cKey Laboratory for Cloud Physics， Chinese Academy of Meteorological Sciences， Beijing， China

An observational study on vertical raindrop size distributions during stratiform rain in a semiarid plateau climate zone

CHEN Yonga， AN Jun-Linga，b， LIU Hui-Zhiaand DUAN Jingc

aState Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry， Institute of Atmospheric Physics， Chinese Academy of Sciences， Beijing， China；bCenter for Excellence in Urban Atmospheric Environment， Institute of Urban Environment， Chinese Academy of Sciences， Xiamen， China；cKey Laboratory for Cloud Physics， Chinese Academy of Meteorological Sciences， Beijing， China

Vertical raindrop size distributions of two stratiform rain events were measured with a Micro Rain Radar during summer 2009 at a semiarid continental site located in Xilinhot， China （43°38′N，116°42′E）. The sequential intensity fltering technique （SIFT） was used to minimize the efect of the spurious variability on disdrometric data to obtain the refectivity—rain rate （Z—R） relationship（Z = aRb）. Compared with the least squares regression （LSR） method， SIFT led to a -5% to 4% change in the coefcient （a） and an 8%—15% increase in the exponent （b） of the Z—R relationship at 300 m. Rainfall estimation using the Z—R relationship with SIFT had lower standard deviation than that with LSR. The vertical variability of the mean rain rate， total raindrop numbers， and parameters （a and b）of the Z—R relationship was small below a melting layer， suggesting that using the radar refectivity of weather radar to estimate stratiform rainfall is relatively accurate， at least in the Xilinhot area.

ARTICLE HISTORY

Revised 29 January 2016

Accepted 7 March 2016

Stratiform rain； vertical drop size distributions； semiarid climate； Micro Rain Radar

雨滴谱随高度变化的观测有助于我们改进雷达估雨精度和认识云雨微物理过程的特征。以往研究较少关注半干旱区的垂直雨滴谱及Z—R关系回归方法的不确定性。在我国半干旱区内蒙古锡林浩特地区，我们使用一台小型垂直指向测雨雷达MRR，观测了两次夏季层状云降雨过程的雨滴谱垂直分布，并利用强度顺序滤波（SIFT）方法计算了Z—R关系。结果表明：这两次层状云降雨过程在零度层以下的平均雨强、平均雨滴总数及Z—R关系的两个参数（a和b）垂直变化较小；利用SIFT方法计算的Z—R关系估算降雨比传统的最小二乘法准确。

1. Introduction

The accurate measurement of raindrop size distributions（RSDs） is important in the calculation of radar rainfall and precipitation scavenging of gases/aerosols， as well as understanding related microphysical processes （Duhanyan and Roustan 2011； Ruan et al. 2014）. Most studies of RSDs focus on their variability in diferent rain types and climate regimes， while few studies consider their vertical structure. The vertical structure of RSDs can be measured by two or more surface instruments positioned at diferent altitudes on a mountain （Levin et al. 1991）， as well as by an airborne particle measuring system （Jia and Niu 2008） or vertical pointing radar （VPR） （Cifelli et al. 2000； Blahak and Beheng 2001； Peters et al. 2005； Tokay et al. 2009； Yoshikawa et al. 2010； Harikumar， Sampath， and Sasi Kumar 2012；Ruan et al. 2014）. Compared with ground measurements along a mountain slope and airborne measurements，observations of vertical microphysical variables using VPRs are more temporally and spatially consistent. Therefore，radar remote sensing has become an important platform for studying the vertical structure of RSDs.

The characteristics of vertical RSDs， such as the total number concentration， radar refectivity Z， rain rate R， and the Z—R relationship， have been presented using VPRs（Cifelli et al. 2000； Tokay et al. 2009； Harikumar， Sampath，and Sasi Kumar 2012； Ruan et al. 2014）. The results of such studies have shown that signifcant diferences occur in the mean rainfall parameters and Z—R relationships for each rainfall category （stratiform/convective） as a function of height， especially in a convective rainfall event. However，study areas have mostly been located in tropical or humid regimes， with few situated in a semiarid regime.

Furthermore， the Z—R relationship derived from the least squares regression （LSR） method can lead to erroneous conclusions due to drop sorting， a small sampling volume， and instrumental noise. The sequential intensityfltering technique （SIFT）， which minimizes the efect of the spurious variability on disdrometric data， was developed by Lee and Zawadzki （2005b） so as to obtain a stable Z—R relationship that is independent of averaging samples. However， few studies have used SIFT to derive the profle of Z—R relationships.

In the present study， the RSD profles of two stratiform rain events obtained from the Xilin River region during the Matter Fluxes in Grasslands of Inner Mongolia as Infuenced by Stocking Rate （MAGIM） project in 2009 were analyzed to present the characteristics of vertical RSD and the Z—R relationship in a semiarid area.

2. Experiment and methodology

2.1. Site and instrument

The experiment was conducted at the Inner Mongolia Grassland Ecosystem Research Station （43°38′N， 116°42′E；1250 m above sea level）， which is located in the Xilin River Basin， Inner Mongolia Autonomous Region， China. The experimental area is located in a semiarid zone. The mean annual precipitation is 323 mm， with ～80% occurring in the growing season from May to September （Chen 1988）. More background on the experiment can be found in Chen et al. （2015）.

The RSDs profle data used in this paper were recorded by a vertically pointing K-band （24 GHz） radar （Micro Rain Radar （MRR）） manufactured by METEK GmbH （Elmshorn，Germany）. The MRR is a frequency-modulated continuous-wave Doppler radar， recording Doppler spectra in 63 bins from 0 to 12 m s-1over 32 range gates （100 m）every 10 s （Peters et al. 2005）. Based on Mie theory and the relationship between terminal fall velocity and drop size （Atlas， Srivastava， and Sekhon 1973）， the single particle backscattering cross section is calculated and used to derive the corresponding profles of RSDs and the integral RSD parameters: radar refectivity factor Z （mm6m-3）， and the rain rate R （mm h-1） （Tridon， Van Baelen， and Pointin 2011）. The procedures used to derive the RSDs， Z， and R are described in detail in Peters et al. （2005）. Only 28 range gates （300—3000 m） of the 32 can be used， because range gate no. 0 （corresponding to 0 m height）， as well as the following two range gates （Nos. 1 and 2； afected by nearfeld efects） and no. 31 （too noisy） are usually omitted from analysis （Maahn and Kollias 2012）. The average time was 1 min and the lowest analysis height was 300 m （based on the range gate of 100 m） in our study.

The accuracy of MRRs is infuenced by vertical wind and turbulence， particularly when the vertical winds are strong （Tridon， Van Baelen， and Pointin 2011）. Therefore，we only used the data from stratiform rain events in this RSD study. The validity of the MRR， through its consistency with a collocated rain gauge， was carried out by examining their measured daily rainfall amounts in summer 2009（Chen et al. 2015）. The MRR1 in Chen et al. （2015） was the instrument used in this paper； it showed good consistency with the rain gauge， with a slope of 1.03 and correlation coefcient of 0.95 （Chen et al. 2015）.

In addition， the antenna of the MRR was checked every week to ensure it was vertically straight and clean. In particular， it was important that no dirt covered the refector. Furthermore， the inclined antenna disk with 26.2° to horizontal line can wash out rainfall quickly on raining days. Therefore， the impact of the antenna on RSD observations was minimized.

2.2. Rain events and their main characteristics

Generally， the existence of a bright band （BB） of radar refectivity is thought to be associated with stratiform precipitation. Through examining the existence of a BB in the time—height cross sections of refectivity from the MRR，two stratiform rain events were determined during the observation period （from 11 July to 14 September 2009）. These two stratiform rain events showed a well-defned BB maintained continuously at around 2.3 km and 1.6 km，respectively， except for a few intermittent periods （Figure 1）. The mean rain rate of the two events was ≤ 1.6 mm h-1（Table 1）.

2.3. Methodology

RSDs are often described using the Marshall—Palmer distribution:

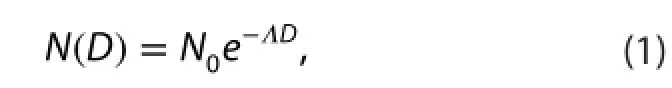
where N（D） is the RSD （m-3mm-1）， N0is the intercept（m-3mm-1）， Λ is the slope （mm-1）， and D is the particle diameter （mm）. Besides， to describe the RSD at diferent heights， the mean rain rate and total drop concentration are analyzed:

Radar rainfall estimation is usually computed from the Z—R relationship. The widely used empirical relationship is a power law:

where a and b are unknown constants. These constants are strongly dependent on the shape of the RSD. Both methods， i.e. LSR and SIFT （Lee and Zawadzki 2005b）， were used in this study.

Figure 1.Time—height cross sections of refectivity and the 300-m rain rate （blue solid line） from the MRR.

Table 1.Characteristics of the rain events measured by the MRR （300 m）.

The basic steps of the SIFT procedure can be summarized as follows （Lee and Zawadzki 2005b）: （i） Z （or R） is calculated from the 1-min RSD for a time window W； （ii） the RSDs are then ordered by increasing Z （or R）； and （iii）a moving average of M （the average sample or size） consecutively ordered RSDs is performed to derive the fltered RSDs. Our study only used the Z to order the RSDs. From these fltered RSDs， we calculated Z and R to obtain a and b in Equation （3）. The window size W is the number of rainy minutes of each stratiform rain event， and the averaging size M is 20 min for both events in our study， because the Z—R relationship is independent of the averaging sample when M ≥ 10 （Lee and Zawadzki 2005b）.

3. Results

3.1. Raindrop size distributions

Figure 2 shows the averaged RSDs of the two stratiform rain events at four levels （300， 800， 1500， and 2000 m）. As can be seen， the RSDs show near exponential decreases as the drop diameter increases. The number concentration of small drops （D ＜ 1.5 mm） mostly decreases with height for both events， while that of larger drops （D ≥ 1.5 mm） is diferent （Figure 2）. However， considering the diferent BB heights （2.3 km/1.6 km） in this two rain events， the vertical RSD in both cases shows a similar trend at 300 m below the melting layer. The number concentration of larger drops （D ≥ 1.5 mm） at that height （2000 m/1300 m） is less than that at lower height， while that of smaller drops is more （Figure 2）， consistent with previous observations of a stratiform rain event in a semiarid area （Jia and Niu 2008）. It is possible that this is caused by insufcient coalescence growth of rain drops at this short distance. Besides， certain diferences exist in the relative variation of the RSD shape between 300 and 800 m for both events， with greater variation in larger drops （D ≥ 1.5 mm） on 23 June. This may be caused by their diferent environmental temperatures and the duration needed to attain a steady equilibrium distribution under the action of coalescence， breakup and evaporation （Hu and Srivastava 1995）.

The mean rain rates of the two rain events （23 July and 26 August） at 300 m are 0.8 and 1.6 mm h-1， respectively（Table 1）. The mean rain rate， total raindrop number， intercepts （N0）， and slope （Λ） on 26 August are larger than those on 23 July （Figure 3）. However， the vertical variability of the mean integral or ftting RSD parameters below the melting layer is small （Figure 3）， consistent with previous fndings in the stratiform region of a mesoscale convective system over Darwin， Australia （Cifelli et al. 2000）.

3.2. Z-R relationships

The scatter of the Z—R relationship on 23 June is less than that on 26 August （Figure 4）. The reduction in the scatter is remarkable and the Z—R relationship becomes more stable when using SIFT， especially for the rain event on 26 August（Figure 4）.

Figure 2.The mean RSD at four height levels.

Figure 3.Vertical distributions of the mean parameters （R and Nt） and ftting parameters （N0and Λ） of RSD.

Figure 4.Scatter of Z—R at 300 m based on LSR （gray open circles） and SIFT （black flled circles）.

The values of a and b in Equation （3） at 300 m when using the two diferent methods are listed in Table 2. When using LSR， the range of a in the Z—R relationship is from 197 to 276， and that of b is from 1.12 to 1.53， for both events （Table 2）. The values are consistent with those reported previously in semiarid or semihumid areas in China （Table 2）.

The value ranges of a and b at 300 m change to 188—288 and 1.29—1.65， respectively， when using SIFT， meaning SIFT leads to a change of -5% to 4% in a， and an increase of8% to 15% in b， compared with LSR. This result is similar that based on two stratiform rain events in Canada （Lee and Zawadzki 2005b）. A larger value of b in Equation （3）indicates a relatively high rainfall intensity for a given refectivity because of the abundance of small drops （Lee and Zawadzki 2005b）. This means that， based on SIFT， the Z—R relationship contains a greater contribution from small drops， because SIFT considers the efect of drop sorting.

Table 2.The Z—R relationship of stratiform rain in diferent regions using the LSR method.

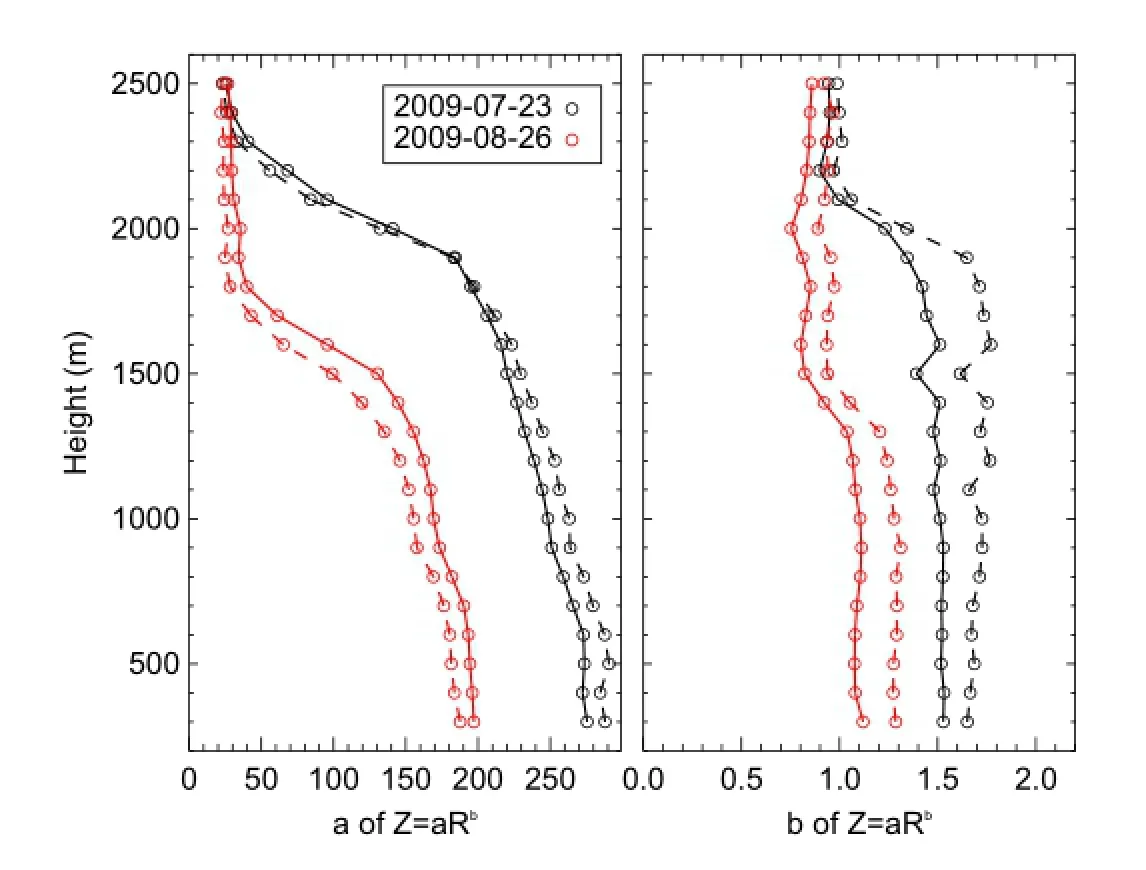
Figure 5.The vertical distributions of parameters of the Z—R relationship based on LSR （solid line） and SIFT （dashed line）.

The vertical variability of the Z—R relationship for the stratiform rain events， below the BB， using both LSR and SIFT， is small （Figure 5）； the relative changes of a and b in Equation （3） （300—1200 m compared with 300 m） using LSR（SIFT） are -13% to 18% （-12% to 22%） and -3% to 5% （3% to 7%）， respectively， for both events， consistent with the observation using LSR by Cifelli et al. （2000）. In other words，the Z—R relationships of stratiform rain events obtained from ground level can represent the profle of the Z—R relationships below the melting layer. Using the Z of weather radar to estimate stratiform rainfall is relatively accurate due to the small vertical variability in the Z—R relationship.

Figure 5 also shows that the relative changes in a （b）when using SIFT and LSR， at heights below the melting layer， are small. Besides， the fuctuation in b when using SIFT， from 1000 to 1400 m， on 23 June， is more obvious than that when using LSR， though it is not large（Figure 5）. The possible cause of the fuctuation is the RSD variability among physical processes throughout this 10-h rainfall event， and the limitation of SIFT. For example， there are more points at 1100 m with a small slope of Z—R when R ＜ 0.1 mm h-1than at 1200 m （fgures omitted）. The scatters of Z—R are more clustered when using SIFT than when using LSR， so the impact on b of the RSD from the low rain rate is greater when using SIFT compared with when using LSR. Therefore， when using SIFT to calculate the Z—R relationship， one must keep in mind the limitations of this method under conditions of a low rain rate and high altitude.

To evaluate the rainfall estimated via the Z—R relationship， the standard deviation （SD） is calculated using the following equation:

where k is the number of data points， R is the rainfall calculated from the RSD within 1 min measured by the MRR， and Rcis calculated by the refectivity with a diferent Z—R relationship. Table 3 lists the SDs based on three rainfall estimation methods: by using Z = 300R1.4， which is widely adopted in operational weather radar rainfall estimation （Fulton et al. 1998）， and by using LSR and SIFT， for both rain events. The results show that using the Z—R relationship obtained using SIFT， for both events， can decrease the standard deviation compared with using Z = 300R1.4. Meanwhile， the SDof only one of the events is lower when using LSR， compared with using Z = 300R1.4. Rainfall estimation using the Z—R relationship with SIFT produces lower SD than with LSR. This is similar to the results of Lee and Zawadzki （2005a）and Yang et al. （2010）， suggesting that SIFT can reduce the efects of RSD variability in rain estimation.

Table 3.The SD （units: mm h-1） of rainfall estimated by three Z—R relationships at 300 m.

4. Summary

This paper reports the characteristics of vertical RSD for two stratiform rain events in a semiarid area， based on observations with a vertically pointing MRR. To minimize the efect of the spurious variability on disdrometric data，SIFT was used to obtain the vertical Z—R relationship. The primary fndings can be summarized as follows:

（1） The variation in the averaged RSD with height for large drops and small drops difered between the two cases， possibly due to their diferent environmental temperatures and the duration needed to attain a steady equilibrium distribution. The vertical structures of RSD parameters （e.g. the mean rain rate， total drop number， the intercept N0， and slope Λ） below the BB were almost uniform.

（2） The ranges of the coefcient （a） and exponent（b） of the Z—R relationship at 300 m when using LSR and SIFT for these rain events were 197—276 and 188—288， and 1.12—1.53 and 1.29—1.65，respectively. The values are consistent with those reported previously for semiarid and semihumid areas in China. Compared with LSR， SIFT led to a —5% to 4% change for a， and an 8% to 15% increase for b， at 300 m. Rainfall estimation using the Z—R relationship with SIFT produced lower SD than that with LSR.

（3） The vertical variability of the Z—R relationship below the BB for the stratiform rain events investigated in this study was small both when using LSR and SIFT. This suggests that using the Z of weather radar to estimate stratiform rainfall is relatively accurate， at least in the Xilin River Basin，due to its small vertical variability in the Z—R relationship.

Disclosure statement

No potential confict of interest was reported by the authors.

Funding

This work was partially supported by the German Research Foundation ［Research Unit 536， MAGIM］； National Natural Science Foundation of China ［grant number 41175105］， ［grant number 41175122］， ［grant number 41505091］， ［grant number 41575124］.

Notes on contributors

CHEN Yong is an assistant professor at the Institute of Atmospheric Physics （IAP）， Chinese Academy of Sciences （CAS）. His main research interests are cloud microphysics and atmospheric environment. His recent publications include papers in Journal of Applied Meteorology and Climatology， Atmospheric Environment， and other journals.

AN Jun-Ling is a professor at IAP， CAS. His main research interests are atmospheric chemistry and atmospheric environment. His recent publications include papers in Atmospheric Chemistry and Physics， Atmospheric Environment， Advances in Atmospheric Sciences， and other journals.

LIU Hui-Zhi is a professor at IAP， CAS. His main research interests are micrometeorology， atmospheric boundary layer physics，and atmospheric environment. His recent publications include papers in Journal of Applied Meteorology and Climatology，Advances in Atmospheric， Science China: Earth Sciences， and other journals.

DUAN Jing is an associate professor at Chinese Academy of Meteorological Sciences. Her main research interests are cloud microphysics and aerosol—cloud—precipitation interactions. Her recent publications include papers Chinese Science Bulletin，Journal of Meteorological Research， and other journals.

References

Atlas， D.， R. C. Srivastava， and R. S. Sekhon. 1973. “Doppler Radar Characteristics of Precipitation at Vertical Incidence.” Reviews of Geophysics 11: 1—35.

Blahak， U.， and K. D. Beheng. 2001. “Measurement of Vertical Profles of Raindrop Size Distributions at Locarno during the SOP: Rain Enhancement by the Seeder/Feeder Mechanism？”MAP Newsletter 15: 250—253.

Chen， Z. 1988. “Topography and Climate of Xilin River Basin.” ［in Chinese.］ In Vol. 3 of Research of Grassland Ecosystem edited by Inner Mongolia Ecosystem Grassland Station， 13—22. Beijing: Science Press.

Chen， Y.， H. Liu， J. An， U. Görsdorf， and F. H. Berger. 2015. “A Field Experiment on the Small-Scale Variability of Rainfall Based on a Network of Micro Rain Radars and Rain Gauges.” Journal of Applied Meteorology and Climatology 54: 243—255.

Cifelli， R.， C. R. Williams， D. K. Rajopadhyaya， S. K. Avery， K. S. Gage，and P. T. May. 2000. “Drop-Size Distribution Characteristics in Tropical Mesoscale Convective Systems.” Journal of Applied Meteorology 39: 760—777.

Duhanyan， N.， and Y. Roustan. 2011. “Below-Cloud Scavenging by Rain of Atmospheric Gases and Particulates.” Atmospheric Environment 45: 7201—7217.

Fulton， R. A.， J. P. Breidenbach， D. J. Seo， D. A. Miller， and T. O'Bannon. 1998. “The WSR-88D Rainfall Algorithm.” Weather and Forecasting 13: 377—395.

Harikumar， R.， S. Sampath， and V. Sasi Kumar. 2012. “Altitudinal and Temporal Evolution of Raindrop Size Distribution Observed over a Tropical Station Using a K-Band Radar.”International Journal of Remote Sensing 33: 3286—3300.

Hu， Z.， and R. C. Srivastava. 1995. “Evolution of Raindrop Size Distribution by Coalescence， Breakup， and Evaporation: Theory and Observations.” Journal of the Atmospheric Sciences 52: 1761—1783.

Jia， X.， and S. Niu. 2008. “Observational Analysis of Raindrop Size Distributions Measured at Surface and Cloud.” ［in Chinese.］Journal of Nanjing Institute of Meteorology 31: 865—870.

Lee， G.， and I. Zawadzki. 2005a. “Variability of Drop Size Distributions: Time-Scale Dependence of the Variability and Its Efects on Rain Estimation.” Journal of Applied Meteorology 44: 241—255.

Lee， G.， and I. Zawadzki. 2005b. “Variability of Drop Size Distributions: Noise and Noise Filtering in Disdrometric Data.”Journal of Applied Meteorology 44: 634—652.

Levin， Z.， G. Feingold， S. Tzivion， and A. Waldvogel. 1991. “The Evolution of Raindrop Spectra: Comparisons between Modeled and Observed Spectra along a Mountain Slope in Switzerland.” Journal of Applied Meteorology 30: 893—900.

Liu， H.， and H. Lei. 2006. “Characteristics of Rain from Stratiform versus Convective Cloud Based on the Surface Raindrop Data.” ［in Chinese.］ Chinese Journal of Atmospheric Sciences 30: 693—702.

Maahn， M.， and P. Kollias. 2012. “Improved Micro Rain Radar Snow Measurements Using Doppler Spectra Post-Processing.”Atmospheric Measurement Techniques 5: 2661—2673.

Niu， S.， X. An， and J. Sang. 2002. “Observational Research on Physical Feature of Summer Rain Dropsize Distribution under Synoptic Systems in Ningxia.” ［in Chinese.］ Plateau Meteorology 21: 37—41.

Peters， G.， B. Fischer， H. Münster， M. Clemens， and A. Wagner. 2005. “Profles of Raindrop Size Distributions as Retrieved by Microrain Radars.” Journal of Applied Meteorology 44: 1930—1949.

Ruan， Z.， H. Ming， J. Ma， R. Ge， and L. Bian. 2014. “Analysis of the Microphysical Properties of a Stratiform Rain Event Using an L-Band Profler Radar.” Journal of Meteorological Research 28: 268—280.

Tokay， A.， P. Hartmann， A. Battaglia， K. S. Gage， W. L. Clark， and C. R. Williams. 2009. “A Field Study of Refectivity and Z-R Relations Using Vertically Pointing Radars and Disdrometers.”Journal of Atmospheric and Oceanic Technology 26: 1120—1134.

Tridon， F.， J. Van Baelen， and Y. Pointin. 2011. “Aliasing in Micro Rain Radar Data due to Strong Vertical Winds.” Geophysical Research Letters 38: L02804. doi: 10.1029/2010GL046018.

Yang， J.， H. Xiao， W. Xiao， and Y. Qin. 2010. “A Study of Raindrop Size Distributions and Their Characteristic Parameters Based on the Methods of SATP and SIFT.” ［in Chinese.］ Journal of Plateau Meteorology 29: 486—497.

Yoshikawa， E.， S. Kida， S. Yoshida， T. Morimoto， T. Ushio，and Z. Kawasaki. 2010. “Vertical Structure of Raindrop Size Distribution in Lower Atmospheric Boundary Layer.” Geophysical Research Letters 37: L20802 doi: 10.1029/2010GL045174.

层状云降雨； 雨滴谱垂直分布； 半干旱气候； 小型测雨雷达

28 October 2015

CONTACT CHEN Yong chenyong@mail.iap.ac.cn

© 2016 The Author（s）. Published by Taylor & Francis

This is an Open Access article distributed under the terms of the Creative Commons Attribution License （http://creativecommons.org/licenses/by/4.0/）， which permits unrestricted use， distribution， and reproduction in any medium， provided the original work is properly cited.