基于Excel运用BWRS方程计算汽液平衡热力学性质*
陈 漓,莫小梅
(百色学院材料科学与工程学院,广西 百色 533000)
专论与综述
基于Excel运用BWRS方程计算汽液平衡热力学性质*
陈 漓,莫小梅
(百色学院材料科学与工程学院,广西 百色 533000)
对于纯流体饱和蒸汽压的计算,由于所联解的BWRS状态方程为高次非线性方程,计算流程涉及多次迭代求根等形式,计算较为繁琐的。而利用Excel便捷的计算功能,通过简单的设计,把流体基本物性数据输入表格中,即可方便求出纯流体汽液平衡相关的热力学性质。
BWRS状态方程;饱和蒸汽压;Excel;热力学性质
在热力学上,相平衡是多种多样的,最为典型的,也是研究最为深入的是汽液平衡。对于纯流体汽液平衡饱和蒸汽压以及饱和汽液相的密度是反映流体热力学性质的重要特性,为此准确测定是很有必要的。然而直接实验测定的数据往往不完整,而运用状态方程计算纯流体的性质是工程中最常用的方法之一。
1 BWRS方程汽液模型
由于多参数状态方程可以在更宽的T、p范围内准确地描述不同物系的pVT关系,尤其是BWRS状态方程在计算纯流体的饱和蒸气压以及相平衡的特性有良好的准确度,以该方程为基础的汽一液平衡模型被认为是当前烃类分离计算中最佳的模型之一。在此我们以BWRS状态方程为模型结合Excel电子表格计算纯流体的饱和热力学性质纯流体的汽、液平衡系统只有一个独立变量,通常取温度T或压强p,一般而言有两类计算;一类是沸点计算一类是饱和蒸汽压计算。
在此我们以蒸气压计算为例说明,并以BWRS方程[1-3]为模型描述纯流体在汽液平衡的两相热力学性质。
(1)
式中:p——系统压强,Pa
T——系统温度,K
ρ——气体或液体的密度,mol·m-3
R——气体常数,8.314J·mol-1·K-1
式(1)中,A0、B0、C0、D0、E0、a、b、c、d、α、γ为状态方程的11个参数。
其逸度系数表达式如下:

(2)
结合汽-液平衡准则式:
lnφv=lnφl
(3)
对于计算纯流体的汽液平衡,首先输入临界参数和偏心因子后,先计算给定温度T下的BWRS方程常数。假设p的初值,求状态方程得到汽相摩尔密度根ρv和液相摩尔密度根ρl,由此判别方程式(3)是否满足收敛条件,若不满足,通过调节p,直到方程式(3)收敛,此时的p、ρv和ρl就是方程组式(1)和式(3)的解。由于整个计算过程需要多次进行试差和迭代运算,如果用手工计算是很繁琐的,一般需借助计算机进行编程计算。然而这对于大多数学生以及初学者而言不易做到,如果能用常用办公软件之一Excel来解决,将对于计算纯流体在汽液平衡下热力学性质带来很大的方便。
Excel具有强大的可视化数据处理功能,它可以进行各种复杂数据处理、统计分析等操作。Excel电子表格还可进行较为复杂的热力学计算,可简单明了地展示计算原理与过程,不仅有利于课堂教学甚至在热力学工程计算方面也有较大的作用[4]。
1.1 饱和蒸汽压的计算
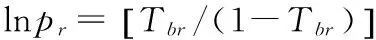
(4)
对于饱和蒸汽压p的迭代式,可从式(3)利用Newton迭代法得到:
(5)
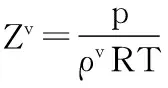
1.2 摩尔密度根的计算
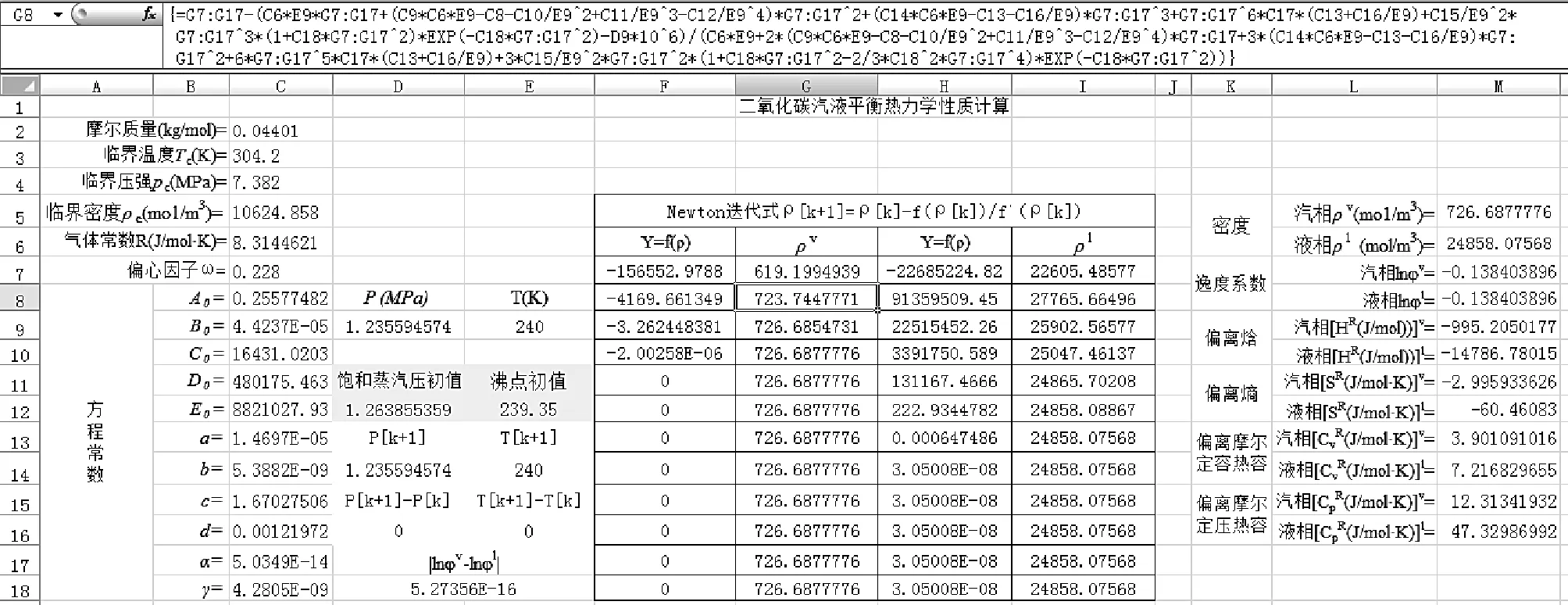
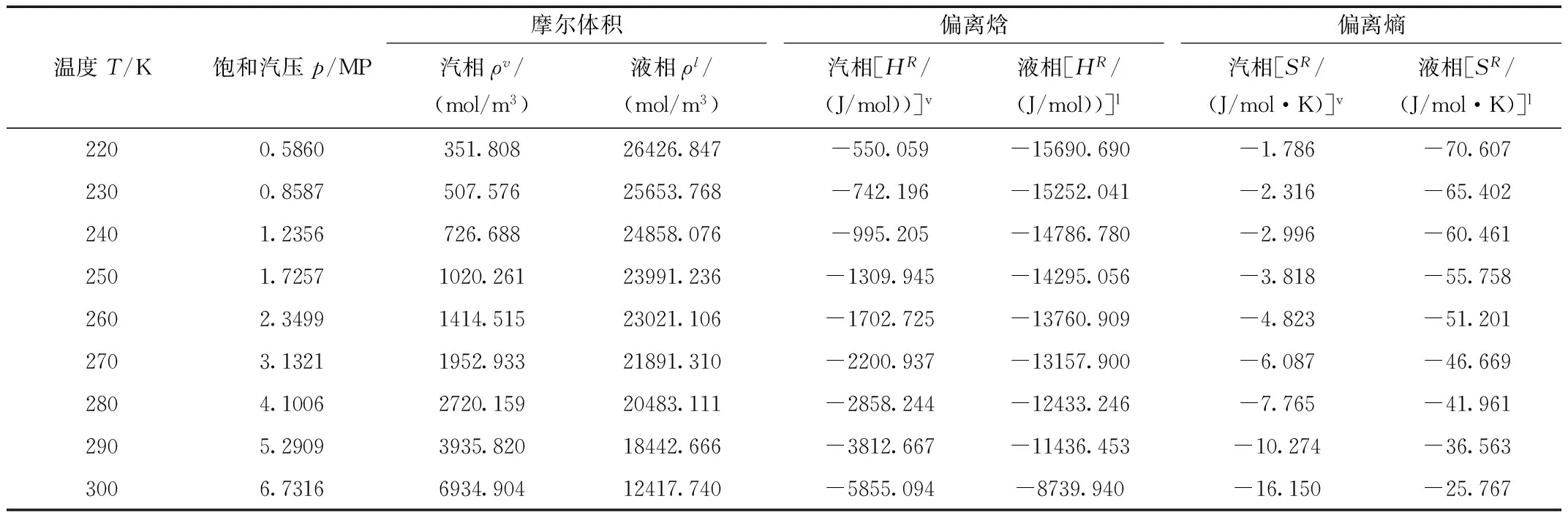
作为多参数状态方程BWRS方程摩尔体积的计算,当T (6) 为了方便迭代,将BWRS方程表示为: 其中: (7) f ′(ρ)为f(ρ)的一阶导。 汽相摩尔密度ρv的求取通常以理想气体密度ρ=p/RT为初值,而液相摩尔密度pl以V=b为初值,代入式(6),得到ρ值后再代入等式右边,一直迭代下去,直到摩尔密度ρ变化很小时就可以了。然而如用手工计算来完成上述的迭代过程是很困难的。利用Excel的计算功能,则可方便同时迭代出ρv和ρl,这样就极大提高计算的效能,且直观的看到整个迭代过程中ρv和ρl数值的变化,对于提高学生的理解能力有很大的帮助。 1.3 其它热力学性质的计算 结合Excel电子表格,BWRS状态方程还可以很方便的计算饱和蒸汽压的其它热力学性质,如偏离焓和偏离熵等热力学性质。 偏离焓: (8) 偏离熵: (9) 利用Excel计算流体的饱和热力学性质,首先要考虑在一定的温度和压强下利用状态方程的PVT关系同时解出ρv和ρl(即当T (1)以CO2为例,分别在C2~C7单元格里输入摩尔质量、临界温度、临界压强、临界密度、气体常数和偏心因子等数值。C8~C18单元格根据临界性质和偏心因子关联BWRS方程的11个常数。如在C9单元格输入“=(0.44369+0.115449*C7)/C5”。 (2)在E9单元格输入某一温度“240”如图1所示,运用式(4)计算饱和蒸气压的初值,即在D12单元格输入“=C4*10^(7*(1+C7)/3*(1-C3/E9))”,把计算数值粘贴到D9单元格里。 (3)在单元格G7和I7分别输入ρv的初值(ρ=p/RT)“=D9*10^6/(C6*E9)”和的初值(ρ=1/B0)“=B8”,单元格G8-G18和I8-I18分别输入Newton迭代式(6),如G8-G18单元格输入如下式子“{=G7:G17-(C6*E9*G7:G17+(C9*C6*E9-C8-C10/E9^2+C11/E9^3-C12/E9^4)*G7:G17^2+(C14*C6*E9-C13-C16/E9)*G7:G17^3+G7:G17^6*C17*(C13+C16/E9)+C15/E9^2*G7:G17^3*(1+C18*G7:G17^2)*EXP(-C18*G7:G17^2)-D9*10^6)/(C6*E9+2*(C9*C6*E9-C8-C10/E9^2+C11/E9^3-C12/E9^4)*G7:G17+3*(C14*C6*E9-C13-C16/E9)*G7:G17^2+6*G7:G17^5*C17*(C13+C16/E9)+3*C15/E9^2*G7:G17^2*(1+C18*G7:G17^2-2/3*C18^2*G7:G17^4)*EXP(-C18*G7:G17^2))}”。同样在I8~I18单元格参照上式输入数组式子,I8~I18单元格式子与G8~G18内容的不同之处仅仅是把式中G7:G17改为I7:I17即可。一般来说大多数情况下迭代5~6次即可得到满意结果如图1所示,为确保迭代的精度我们进行了11次迭代,单元格G18和I18得到的数值分别为ρv和ρl。单元格F7~F18和H7~H18分别为式(7)中f(ρ)的ρv和ρl收敛情况。 (5)计算其它的热力学性质,在单元格M9到M16分别输入式(8)、式(9)、式(10)、和式(11),这样我们同时得到二氧化碳汽相和液相偏离焓、偏离熵、偏离定容摩尔热容和偏离定压摩尔热容等数值。例如在单元格M9输入“=(C9*C6*E9-2*C8-4*C10/E9^2+5*C11/E9^3-6*C12/E9^4)*M5+1/2*(2*C14*C6*E9-3*C13-4*C16/E9)*M5^2+1/5*C17*(6*C13+7*C16/E9)*M5^5+C15/(C18*E9^2)*(3-(3+C18*M5^2/2-C18^2*M5^4)*EXP(-C18*M5^2))”计算得到的数值为汽相偏离焓。 为了检验Excel在计算纯流体饱和性质的可靠性,我们以二氧化碳为研究对象,对该气体饱和蒸汽压等性质进行计算。在单元格C3、C4和C5分别输入二氧化碳的临界温度Tc和临界压强pc和临界密度ρc,单元格C7输入偏心因子ω的数值参见图1,计算二氧化碳温度为220~300 K的饱和蒸汽压、摩尔体积和偏离性质。计算的结果参见表1。 图1 二氧化碳饱和性质的计算 温度T/K饱和汽压p/MP摩尔体积汽相ρv/(mol/m3)液相ρl/(mol/m3)偏离焓汽相[HR/(J/mol))]v液相[HR/(J/mol))]l偏离熵汽相[SR/(J/mol·K)]v液相[SR/(J/mol·K)]l2200.5860351.80826426.847-550.059-15690.690-1.786-70.6072300.8587507.57625653.768-742.196-15252.041-2.316-65.4022401.2356726.68824858.076-995.205-14786.780-2.996-60.4612501.72571020.26123991.236-1309.945-14295.056-3.818-55.7582602.34991414.51523021.106-1702.725-13760.909-4.823-51.2012703.13211952.93321891.310-2200.937-13157.900-6.087-46.6692804.10062720.15920483.111-2858.244-12433.246-7.765-41.9612905.29093935.82018442.666-3812.667-11436.453-10.274-36.5633006.73166934.90412417.740-5855.094-8739.940-16.150-25.767 同样也可以以蒸汽压p为独立变量来进行沸点的计算,只需在单元格E14输入如下的迭代式即可。 通过上面实例可以看出,用Excel解决进行纯流体汽液两相饱和性质的计算,运算过程中的重复操作很方便,整个表格的计算内容具有通用性,且可根据教学需要自行扩充完善,如增加偏离定容热容和偏离定压热容的计算。整个运算过程没有涉及编程等复杂设计,便于教学讲解演示,也可用于工程计算。 [1] Strling K E, Han M S.Thermo Data Refined for LPG (Part 14: Mixture)[J].Hydrocarbon Processing, 1972, 51(5): 129-132. [2] 苑伟民,贺三,袁宗明,等.求解BWRS方程中压缩因子的数值方法[J].管道技术与设备,2009(3):14-16. [3] 吴玉国,陈保东.BWRS方程在天然气物性计算中的应用[J].油气储运,2003,22(10):16-21. [4] 武新伟.ExceI在BWRS方程密度迭代中的应用[J].能源与节能,2014,100(1):148-151. [5] 陈新志,蔡振云,胡望明,等.化工热力学.3版[M].化学工业出版社,2009:44-45. Vapor Liquid Equilibrium Thermodynamic Properties Using BWRS Equation Calculation Based on Excel* CHENLi,MOXiao-mei (School of Materials Science and Engineering, Baise University, Guangxi Baise 533000, China) The saturated vapor pressure was calculated for pure fluids, due to the combined solution BWRS equation of state for higher order nonlinear equation, the process involved multiple iterations root and other forms of computing more complicated.Using Excel convenient calculation function, with simple design, the basic physical properties of the fluid were input in form, the relevant thermodynamic properties of pure liquid-vapor equilibrium can easily be found. BWRS equation of state; vapor pressure; Excel; thermodynamic properties 广西高校科学技术研究项目(2013YB244)。 陈漓(1962-),男,副教授,主要从事热力学研究。 O642 A 1001-9677(2016)019-0001-03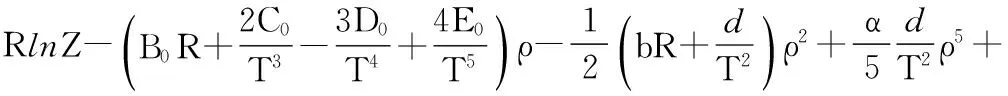
2 利用Excel进行纯流体饱和热力学性质的计算

3 应用分析
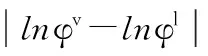
4 结 论

