媒体报道对传染病传播控制的影响

马芙玲

（中山火炬职业技术学院公共课部，广东中山528436）

媒体报道对传染病传播控制的影响

马芙玲

（中山火炬职业技术学院公共课部，广东中山528436）

建立一个三维房室模型，用于研究媒体报道对传染病在某一地区的影响.该模型的稳定性分析表明：基本再生数R0＜1时，无病平衡点是全局渐近稳定的；如果R0＞1，则一个独特的地方病平衡点出现，它是渐近稳定的；在特殊情况下，地方病平衡点是全局稳定的.根据理论结果讨论媒体报道在传播中的作用.

SIRS模型；媒体报道；稳定性

0　引言

当一种传染病在一个地方传播时，政府疾控部门将尽最大努力预防疫病传播.措施之一是尽快通过媒体宣传教育，使人们得到正确预防疾病的知识.掌握预防疫病的知识越多，越能预防疫病的传播.通过研究孟加拉国已婚夫妇中爱滋病传染的统计分析可知，宣传教育在提高大众公共卫生意识、预防爱滋病传染起了重要作用，接受宣传教育的人与没有接受宣传教育的人染病率分别是4.67％和77.73％［1］.2002年11月，非典作为一种新的传染性感染疫病首次在中国广东出现，随后在亚洲乃至在全球一定范围内传播.那时媒体宣传教育对整个疫情传播起了很大的抑制作用；因此，有必要研究建立一个媒体宣传教育对传染病影响的模型，分析比较媒体宣传教育对传染病传播的作用.

最近有学者在研究媒体报道对传染病传播的作用时，讨论心理因素影响感染人数和入医院人数［2］.用房室模型探索多个暴发新传染病的情形［3］.用有接触速度的SEI模型从理论上研究媒体报道对传染病动态的影响［4］.

本文通过用新接触速度μe-mI建立一个SIRS模型，纳入了媒体对疾病传染的影响因子，通过计算研究媒体报道对传染病传播动态影响的理论结果.

1　与媒体传播有关的SIRS模型

考虑到传染病在某地区有一定的传染，将此地区人口分为三类：可疑者、感染者和恢复者，分别用S（t），I（t）和R（t）表示.建立一个与媒体传播有关的标准SIRS模型［5］：

其中：r为易感染者的抽样数；γ为感染者的恢复率；d为自然死亡数；α为相关传染病死亡数；β（I）=μe-mISI为疾病传播期值，用来表示特定个体病毒感染的传播速度；δ为免疫丧失率；m为媒体传播与传染病传播速度的影响因子，若m=0，感染速率是常数；当m＞0时，传染病者的增加速率减慢.假定所有参数都是正常数.

有研究者用房室模型及繁殖模型验证模型（1）的基本再生数，在无病平衡点是局部稳定的［6］.现用2个向量表示新传染病周期和传染条件.

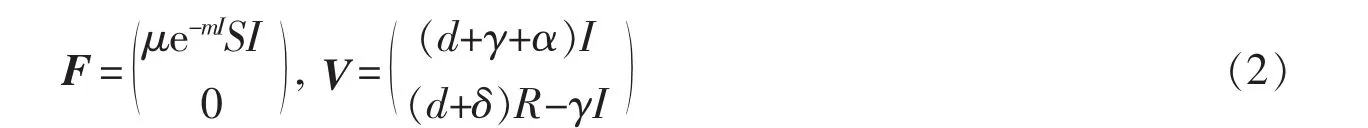
对受感染者组成I和R计算如下：

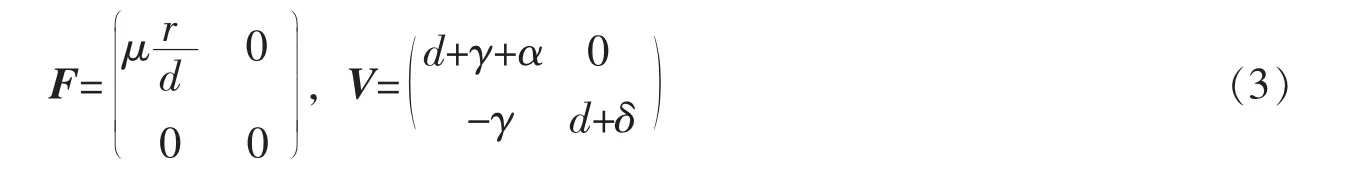
这里，F是非负数，V是非奇异M－矩阵；因此，FV-1是非负数，且

由ρ（FV-1）得基本再生数：

讨论R0的符号，有以下定理：

定理1.1对于系统模型（1），若基本再生数R0＜1则无病平衡点E0是稳定的；若R0＞1则是不稳定的.

计算得到系统模型（1）在平衡点E0的特征方程：

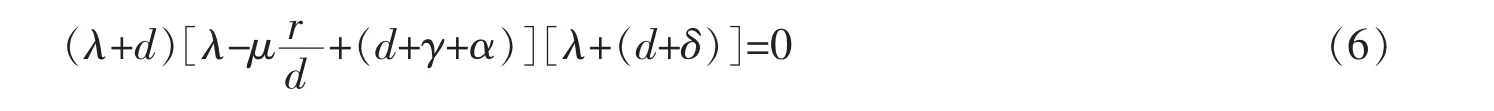
根据Routh－Hurwitz准则，当且仅当R0＜1，所有特征值是负数.

定理1.2系统模型（1）初始条件为：S（0）≥0，I（0）≥0，R（0）≥0，在连续正区间D=｛（S，I，R）∈R3|0＜内，模型（1）的解正有界.

则有：

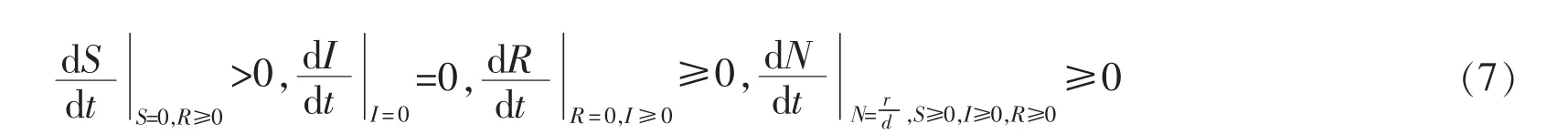
因此，在连续内建立的系统模型（1），所有解为正且有界.

定理1.3如果基本再生数R0＜1，无病平衡点E0在全局D内是处于无发病稳定状态.

证明：选择Lypunov函数V=1计算系统模型（1）中V的导数，得：

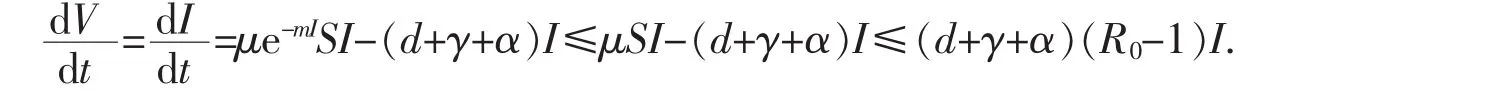
2　地方性传染病平衡的存在

若m=0，即人们还没受到媒体影响，可验证当R0＞1，系统模型（1）在出现特有的传染病平衡状态.即：

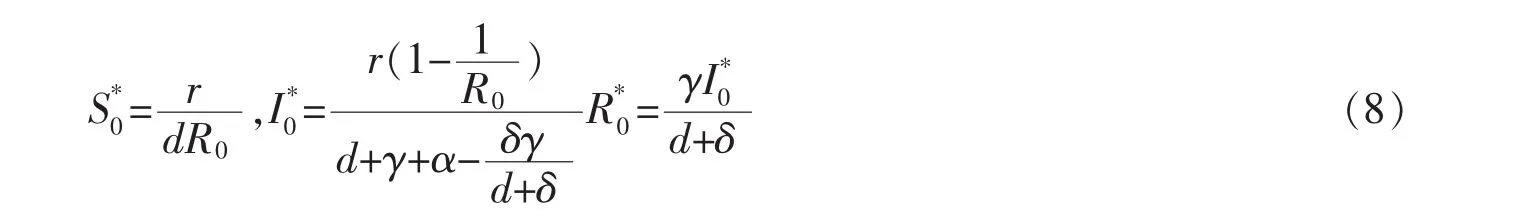
如果考虑到媒体和心理因素影响，则平衡如下：

由式（10）得：

由式（9）、式（10）得：

调递增指数函数.

由此得到系统模型（1）特有的传染病平衡点（S*，I*，R*），有：

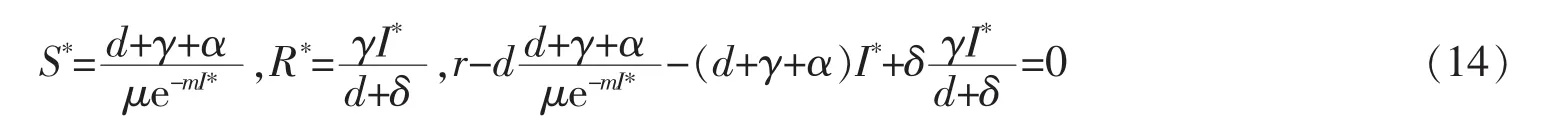
3　传染病平衡的稳定

定理3.1若R0＞1，m=0传染病在平衡点是局部渐近稳定的.

证明：容易得到相关特征方程：

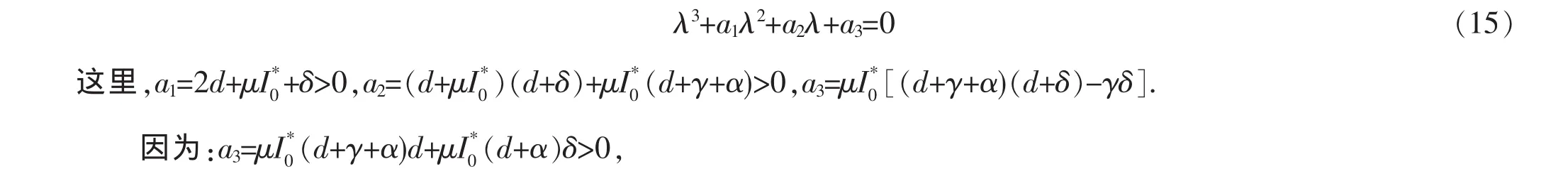
计算可得：a1a2-a3＞0.

方程（15）的所有特征根都是负数，由Routh－Hurwitz准则，当R0＞1时，是局部渐近稳定的［7］.

定理3.2如果R0＞1，m＞0，传染病在平衡点是局部渐近稳定的.

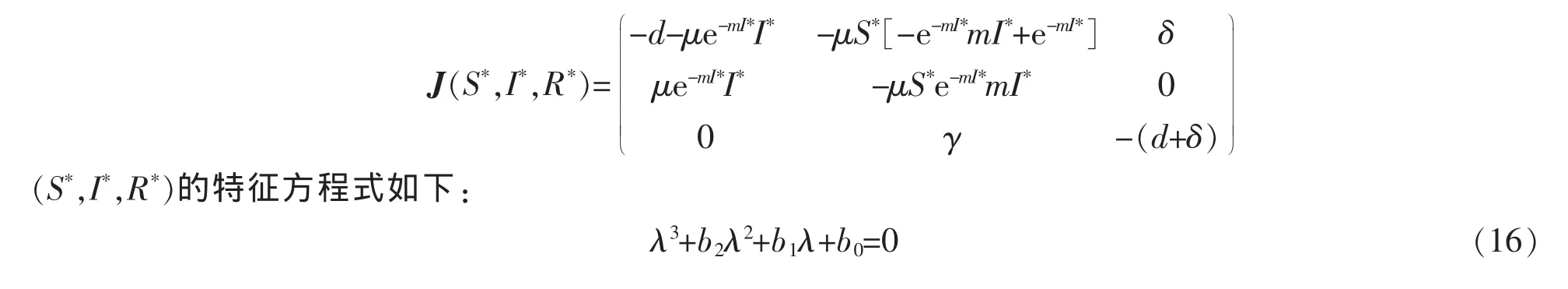
证明：讨论Jacobian平衡矩阵这里，b2=μS*e-mI*m I*+2d+δ+μe-mI*I*，b1=（2d+δ）μS*e-mI*m I*+d（d+δ）+μe-mI*I*（d+δ+μS*e-mI*），b0=d（d+δ）μS*e-mI*m I*-μe-mI*I*γδ+（d+δ）μS*e-mI*μe-mI*I*.

很明显，由Routh－Hurwitz标准，当b2＞0［7］时，容易证明：b0＞0，b2b1-b0＞0.

方程（15）的所有特征根为负，由Routh－Hurwitz准则，当R0＞1，m＞0时（S*0，I0*，R*0）是局部渐近稳定的［8］.

综上所述，当R0＞1时，能得到传染病局部地区渐近稳定.对特殊情况当δ=0时，可以证明当R0＞1时，相应地方特有的传染病趋于渐近稳定.

4　模型（1）中δ=0的特殊病例

在系统模型（1）中若δ=0，得到如下SIRS模型：

易见模型（17）前2个方程独立于第3个方程，故只需讨论以下模型：

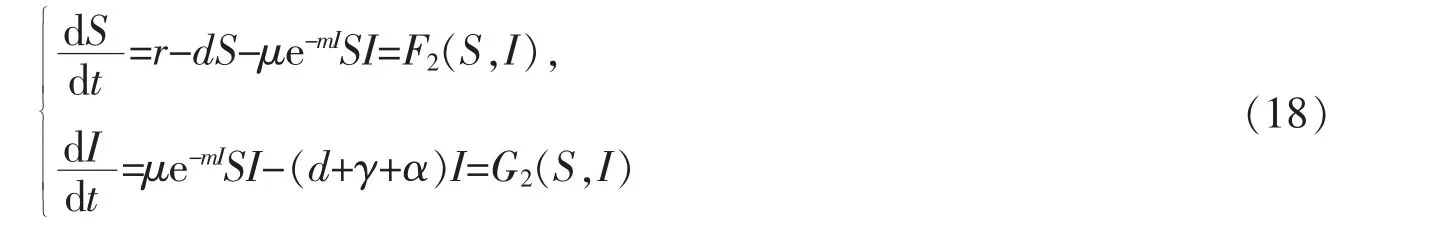
让方程（18）右边为零，能证明R0＜1时，模型（18）有一个无病平衡点是全局渐近稳定的，且

当m=0时，得到如下SIRS模型：

它是模型（18）的特例.

容易证明，当R0＞1时局部地区病情趋于稳定.

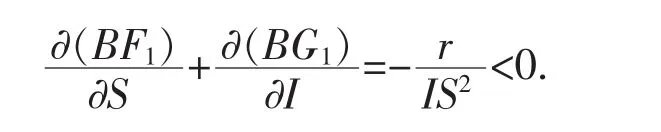
由Bendixson－Dulac准则，在D1范围内无传染迹象；因此，若R0＞1，在全局范围内是渐近稳定的.

当m＞0时，容易证明模型（18）当R0＞1时，在平衡点是局部渐近稳定的.

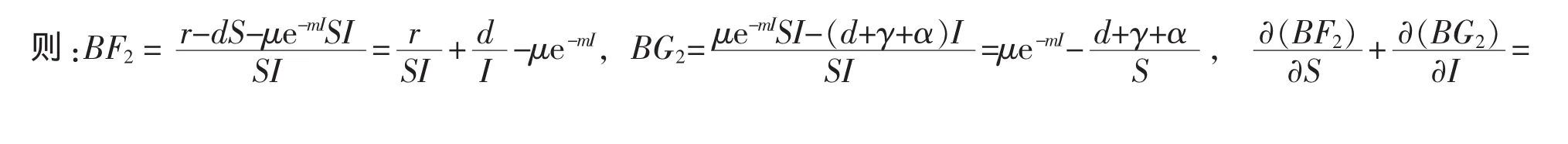
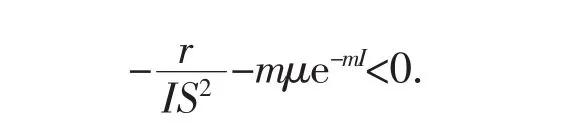
根据Bendixson－Dulac标准，当R0＞1时，模型（18）在平衡点是局部渐近稳定的.

5　数值模拟

通过数值对系统模型（1）进行模似计算，显示媒体对传染病的一些影响.选取参数μ=0.002，r=5，d=0.02，α=0.1，γ=0.05，δ=0.01时，R0=2.94＞1.模型（1）存在一个独特的地方病平衡点.如图1所示，当m=0，无媒体报道的影响，疾病流行出现一个峰值平衡.从图2可明显看出，当m＞0时，即有媒体报道的影响，此时感染者数量很少，当m变得较大时感染者数量更少，这些表明媒体传播能够影响人群感染数量.

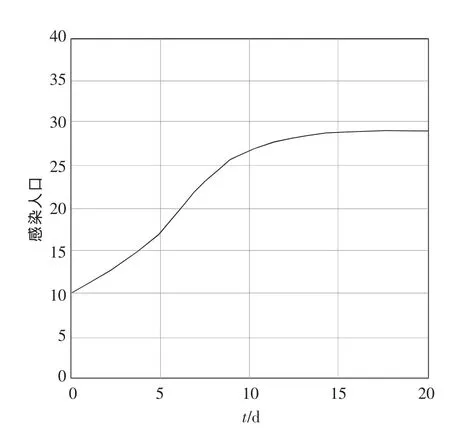
图1　m＝0时媒体宣传的影响曲线Fig.1 The curve represent e the case when m＝0.

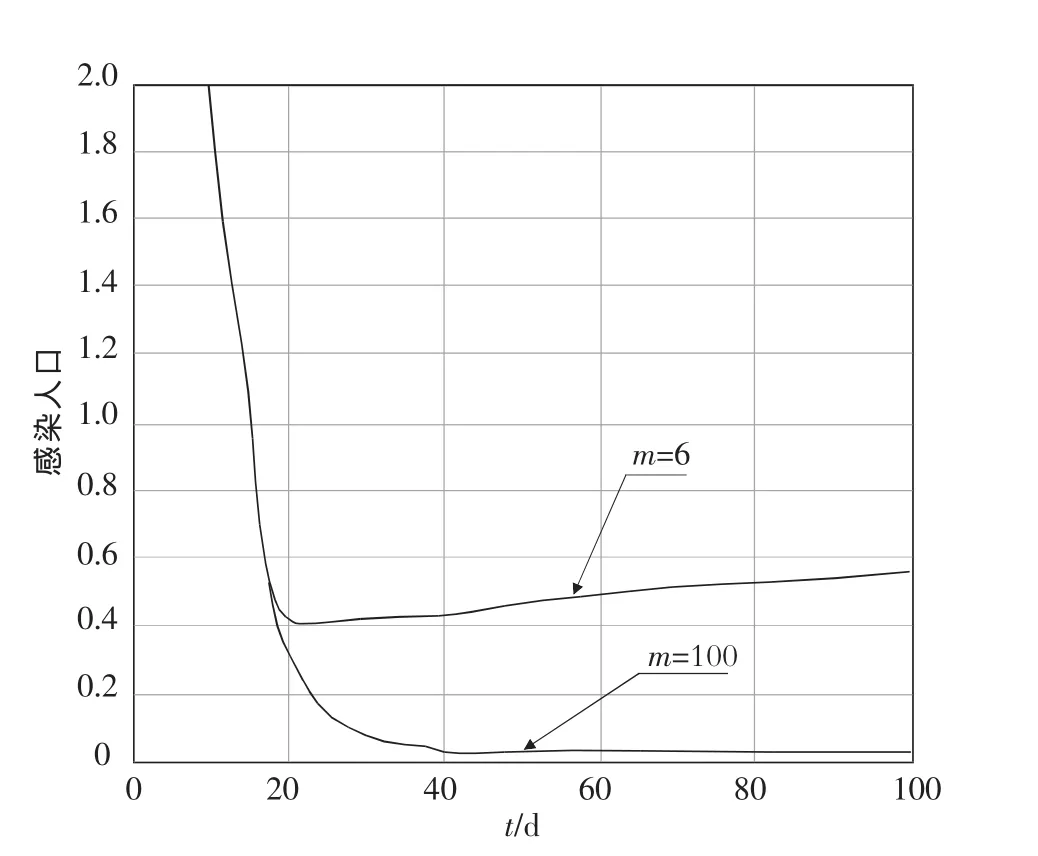
图2　m＝6和m＝100时媒体宣传的影响曲线Fig.2 The curve represent e the case when m＝6 and m＝100.

6　结论

通过分别研究无病平衡和传染病模型（1）、模型（17）的平衡，研究了受媒体传播影响的SIRS模型.首先，当m=0时，分别比较模型（1）和模型（17）的动态，得出媒体传播不能改变病毒基本再生数R0和平衡值；其次，m值只改变流行平衡坐标，R0＞1时流行病平衡在局部的稳定性是保持不变的.

［1］RAHMAN M S，RAHMAN M L.Media and Education Play a Tremendous Role in Mounting AIDS Awareness among Married Couples in Bangladesh［J］.Aids Research and Therapy，2007，4（10）：10－17.

［2］LIUR，WU J，ZHU H.Media／Psychological Impact on Multiple Outbreaks of E merging Infectious Disease［J］.Computational and Mathematical Mathods in Medicin，2007，8（3）：153－164.

［3］CUI J，S UN Y，Z H UH.The Impact of Media on the Control of Infectious Disease［J］.Journal of Dynamics and Differential Equations，2008，20（1）：31－53.

［4］LIU Yi-ping，CUI Jing-an.The Impact of Media Coverage on the Dynamics of Infectious Disease［J］.International Journal of Biomathematic,2008，1（1）：65-74.

［5］VAN DEN DRIESSCHE P，WATMOUGH J.Reproduction Numbers and S ub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission［J］.Math.Biosci，2002,180(1-2)：29-48.

［6］王琦，秦斌，陈占和，等.一类差分方程组的全局渐进稳定性［J］.广西工学院学报，2011，22（2）：74-77，85.

［7］王琦，张更容，韩松，等.一类高阶线性差分方程的全局稳定性［J］.广西工学院学报，2013，24（2）：33-35.

［8］MURRAY JD.Mathematical Biology［M］.Berlin：Springer-Verlag，1998.

（学科编辑：张玉凤）

Influence of media coverage on the spread and control of infectious diseases

MA Fu-ling
（Department of Public Courses,ZhongShan Huoju Polytechnic,Zhongshan 528436,China）

We develop a three dimensional compartmental model to investigate the impact of media coverage on the spread and control of infectious diseases(such as SARS)in a given region/area.Stability analysis of the model shows that the disease-free equilibrium is globally-asymptotically stable if a certain threshold quantity,the basic reproduction number R0＜1,is less than unity.But if R0＞1,it is shown that a unique endemic equilibrium appears, which is asymptotically stable.On a special case,the endemic equilibrium is globally stable.We discuss the role of media coverage on the spreading based on the theory results.

SIRS model;media coverage;stability.

O175

A

2095-7335（2016）03-0116-06

10.16375/j.cnki.cn45-1395/t.2016.03.020

2016-02-25

教育部高等学校博士学科点专项科研基金教师类资助课题（20120172120050）资助.

马芙玲，学士，副教授，研究方向：微分方程模型，E-mail：flima＠sina.com.