在线低秩表示的目标跟踪算法

王海军,葛红娟,张圣燕

(1.南京航空航天大学民航学院,江苏南京 210016; 2.滨州学院山东省高校航空信息技术重点实验室,山东滨州 256603)

在线低秩表示的目标跟踪算法

王海军1,2,葛红娟1,张圣燕2

(1.南京航空航天大学民航学院,江苏南京 210016; 2.滨州学院山东省高校航空信息技术重点实验室,山东滨州 256603)

针对传统的基于生成模式的跟踪方法对噪声及遮挡问题比较敏感,导致跟踪结果失败的问题,提出了以前几帧的跟踪结果作为观测矩阵,采用鲁棒的主元成分分析模型求解观测模型的低秩特征.当新的视频流到来时,不是把所有的跟踪结果矩阵作为观测矩阵.并提出了新的增量鲁棒的主元成分分析模型,采用增广拉格朗日算法求解新矩阵的低秩特征,并以此低秩矩阵在贝叶斯框架下建立跟踪模型,用恢复的低秩特征更新字典矩阵.将文中方法与其他6种跟踪算法在8种跟踪视频上进行跟踪对比.实验结果表明,所提出的方法具有较低的像素中心位置误差和较高的重叠率.

目标跟踪;低秩特征;鲁棒的主成分分析模型;字典矩阵

目标跟踪是计算机视觉领域一项重要的研究课题,在视频监控、交通流量控制、辅助驾驶系统、人机接口等方面得到了广泛的应用.近年来,国内外许多学者提出了很多鲁棒的目标跟踪算法,取得了较好的跟踪性能.目前,目标跟踪算法主要分为两种类型:判别模式[1-2]和生成模式[3-6].

判别模式将目标跟踪看成把跟踪目标从背景目标块中分离出来的二值分类问题,这类方法的运算耗时少,可实现实时的目标跟踪;生成模式将跟踪问题看成是从候选样本中选出与目标区域重构误差最小的样本作为跟踪目标,可以实现鲁棒的目标跟踪,跟踪精度较高,但是耗时大,难以实现实时跟踪.文献[5]提出了增量在线目标跟踪算法,在粒子滤波框架下,通过增量主成分学习在线学习跟踪目标的外观模型,实现目标的跟踪.文献[3]将稀疏表示应用到目标跟踪领域,并提出用琐碎模板解决跟踪过程中出现的遮挡问题,但是该方法用Lasso方法来求解l1范数最小化问题,导致计算量大,实时性低,且跟踪目标的像素较低,难以充分利用跟踪目标的特征信息.文献[7]提出了用加速近似梯度算法代替Lasso方法来求解l1范数最小化问题,实现了快速跟踪.文献[8]提出了一种基于稀疏原型的在线目标跟踪算法,该算法对跟踪过程中出现的异常噪声进行显式处理,降低了l1算法的计算量,提高了跟踪精度和速度.

虽然判别模式和生成模式都能够对目标进行准确跟踪,但是判别模式当跟踪目标出现大面积的遮挡时,难以实现准确的跟踪,且很难解决跟踪过程中出现的尺度变化问题.而在生成模式中,大多数方法采用的字典矩阵是由已得到的跟踪结果组成的,当跟踪结果出现遮挡或漂移时,就会对后来的跟踪产生漂移,引起跟踪误差.

为解决上述问题,笔者提出了一种基于增量低秩特征的目标跟踪算法,在线地学习跟踪目标的低秩特征,恢复跟踪目标被遮挡的部分,并更新字典矩阵.同时,该方法能准确恢复跟踪目标的全局子空间,解决了以往基于子空间跟踪方法对噪声不鲁棒,以及跟踪出现遮挡时跟踪失败的问题.

1　低秩特征

鲁棒的主元成分分析(Robust Principal Component Analysis,RPCA)[9]在计算机视觉领域得到了广泛的应用,该方法假定观测到的受污染数据矩阵Y∈Rm×n由低秩矩阵D和噪声矩阵E构成,即Y=D+E,其中,D和E是未知的.为从污染矩阵Y中恢复低秩矩阵D,可用下面的数学模型来描述:

但是,式(1)假定观测数据Y是从一个子空间提取来的,如果观测数据Y是从多个子空间取样来的样本,若继续采用式(1)来恢复低秩特征D,则将存在误差.为了更准确地获得低秩特征矩阵D,文献[9]提出了更加一般化的秩最小化数学模型,即

但是式(1)和式(2)求得的干净矩阵是在所有观测数据组成一个污染矩阵Y的基础上求得的,当有新的数据到来时,需要把新的数据和原有的观测矩阵组成新的观测矩阵,重新进行核最小化计算以求得低秩特征,这样就大大降低了计算效率.为解决这个问题,在式(1)和式(2)的基础上,提出了增量求解低秩特征的算法,并应用到目标跟踪算法上,取得了较好的效果.

2　基于在线低秩特征的目标跟踪算法

2.1在线低秩特征学习

当对一段视频中的目标进行跟踪时,首先用手选方法将前k帧中跟踪目标提取出来,组成一个前k帧的标准跟踪结果的矩阵.然后用

进行前k帧的低秩特征Dk计算,并采用文献[9-11]的方法对Dk进行不足奇异值分解(Singular Value Decomposition,SVD)计算,即

其中,Uk为前k帧的子空间基底,Σk为半正定对角矩阵.

当有新的视频帧时,即第k+1帧来临时,如果采用原始方法,则需组成包括前k帧的观测矩阵,重新进行计算式(3),计算效率大大降低.为了解决这个问题,采用式(2)在线计算低秩矩阵D.式(2)的求解是凸优化问题,为求解Z和E,文中采用增广拉格朗日乘子(Augmented Lagrange Multiplier,ALM)算法[12].首先,把式(2)转化为下面等价问题:

式(5)可通过Inexac ALM来求解,即

其中,Y1和Y2是拉格朗日乘子;μ＞0,是惩罚参数.使用In ALM解式(6)中的优化问题的算法如下:

输入:一个观测图像块(向量形式)Y,子空间基底U,这里令A=U,参数λ.

初始化:Z=J=0,E=0,Y1=0,Y2=0,μ=10-6,ρ=1.1,ε=10-8.

While不收敛do

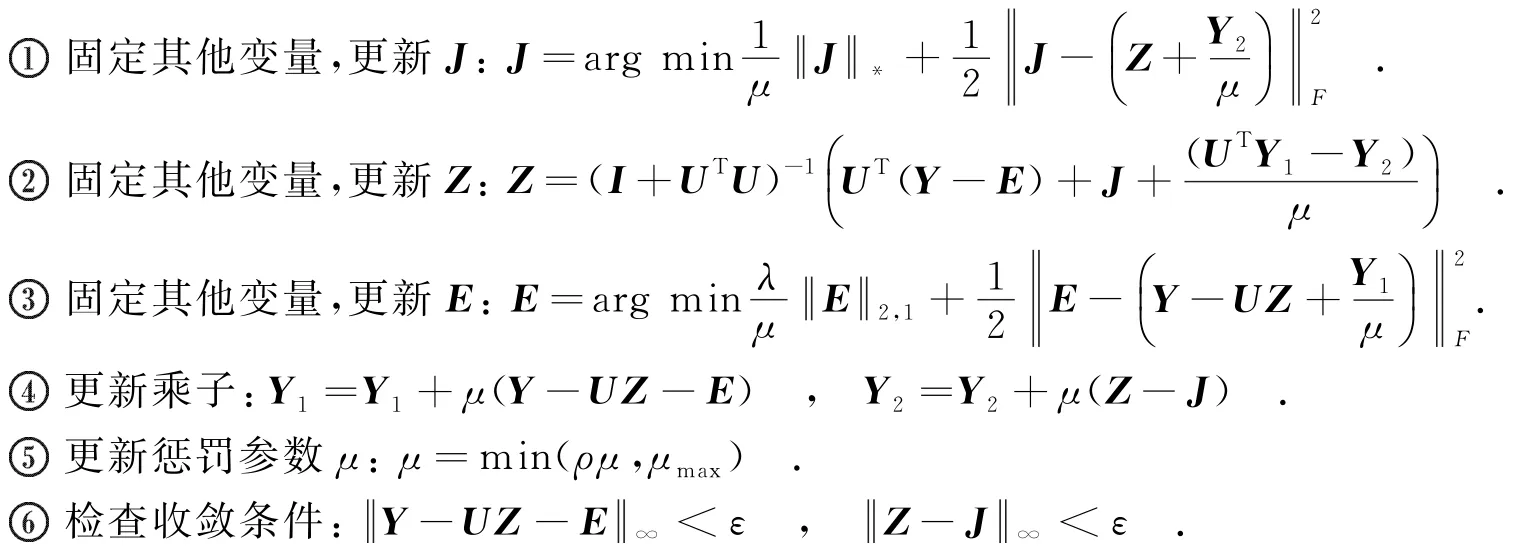
End while.

求出新的Z后,则增量低秩特征D=UZ.

2.2运动模型

目标跟踪可以看成是隐式马尔科夫模型下的贝叶斯推理问题,假定已知前t帧的观测数据Yt={y1,y2,…,yt},则t时刻的状态变量xt可通过迭代求解获得,即

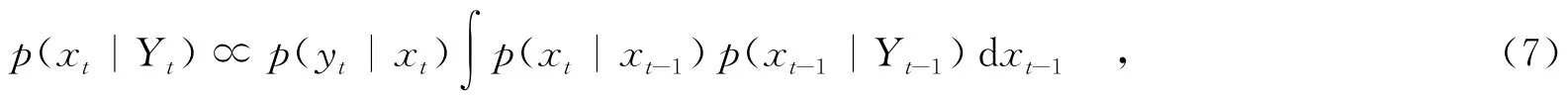
其中,p(xt|xt-1)表示连续两个状态之间的运动模型;p(yt|xt)为似然函数或观测模型;xt为仿射变换的6个参数,用来表征连续两帧跟踪目标的运动状态.xt={zt,pt,θt,st,αt,φt},分别用来表示跟踪目标的坐标位置、旋转角度、尺度变化、宽高变化和斜交变化等.运动模型p(xt|xt-1)=N(xt|xt-1,Σ),其中Σ为状态xt的6个参数的对角协方差矩阵.

2.3观测模型

由式(3)可知,由前k帧视频跟踪结果组成矩阵可求出低秩特征,当有新的视频流时,可通过式(4)求出新的视频流的低秩特征,其中,i为第k+1帧的第i个样本.因此,判断第i个样本是否为跟踪目标,可通过如下观测模型判断:

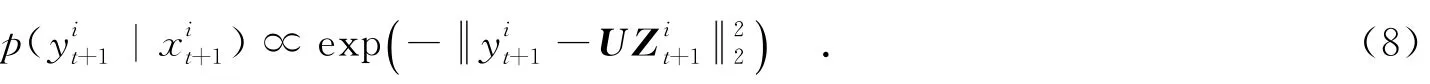
式(8)为第t+1帧中第i个样本为跟踪目标的概率.当跟踪目标出现遮挡时,采用文献[8]中方法,引入一个掩模向量,来指示误差向量E中的零元素与非零元素,即

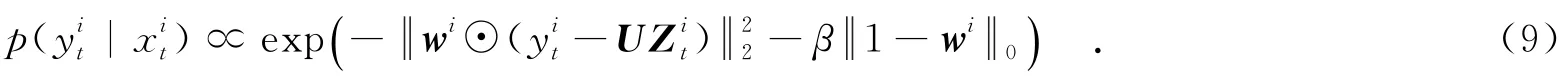
当误差向量Ei中第j个元素为0时,则;否则,.☉表示对应元素相乘.

2.4在线更新

为更好地适应跟踪过程中运动目标的变化,需要对子空间基底U进行更新,当时,t为一阈值,为误差向量中非零元素的个数,l(Et)为误差向量中元素的个数,则重新采用式(3)计算低秩特征,这时的视频流矩阵由开始的前20帧跟踪目标与最新10帧的跟踪目标组成,这样既保留了原始跟踪目标的信息,又能适应跟踪过程中目标的变化.

3　实验结果

文中算法在Window 7操作系统、Pentium Dual-Core CPU、2 GB内存电脑平台采用Matlab软件进行仿真实验.为了验证文中方法的优越性,采用8个具有挑战性的视频与当前比较流行的6种算法进行比较.这些视频为Occlusion1、Caviar1、Singer1、Car4、Car11、DavidIndoor、David Outdoor、Stone,分别具有光照变化、尺度变化、背景混乱、遮挡以及姿态变化等影响跟踪效果的因素.6种算法分别为:Frag[13]、L1[3]、MIL[1]、PCA[5]、PN[14]、VTD[15]等.每组视频第1帧跟踪目标的位置手动标出,文中算法每种视频跟踪采用的粒子数目为600,其他方法的参数分别采用其具有最优性能的参数.

3.1定性比较

图1(a)为Occlusion1视频的跟踪结果,图中女孩头部位置基本不发生变化,但是存在来自左边、下方、右边图书的严重遮挡.从跟踪结果看,大部分方法基本上都能对女孩头部进行跟踪,但是PCA和MIL算法存在偏移.VTD算法尺度变化的太大,导致跟踪结果方框不能覆盖女孩的头部.文中算法采用了考虑遮挡的模型及在线更新机制,能够准确跟踪女孩的头部位置.

图1 不同视频采用不同算法跟踪结果对比图

图1(b)为Caviar1视频的跟踪结果.Caviar1视频存在相似人物的遮挡,跟踪目标人物本身也存在运动以及尺度变化,同时视频场景中存在光照变化.Caviar1视频中目标人物由近及远逐渐移动,目标人物尺度逐渐变小,同时存在来自右边人物的遮挡.文中算法由于采用基于低秩特征,同时引入遮挡机制以及仿射变换方法,所以当出现相似人物遮挡时,也能准确地对目标人物进行跟踪,同时适应目标人物尺度的变化.MIL算法基于多示例的方法,当出现相似人物的干扰时,偏移目标人物比较大.

图1(c)～(f)分别为Singer1、Car4、Car11和DavidIndoor视频的跟踪结果.Singer1视频为穿白衣的歌者在强烈白光照射下演唱的视频片段.该视频中跟踪目标存在严重的光照变化,同时由于摄像机的运动,使得跟踪目标存在尺度变化.MIL和Frag算法没有考虑尺度变化,所以不能准确对目标进行定位跟踪.PN算法虽然考虑了尺度变化,但是不能跟上目标的变化速度.文中算法、VTD和PCA算法能够较准确地对歌者目标进行跟踪;在Car4视频中,目标汽车和道路以及公路两旁树木的颜色较为相近,同时汽车过桥时,存在由亮到暗以及由暗到亮的光照变化.MIL和Frag算法没有考虑尺度变化,出现了飘移现象.文中算法、PCA及L1算法较为准确地对目标汽车持续跟踪;在Car11视频中,目标汽车在夜晚的公路上快速行驶,存在来自对面汽车灯光严重的干扰.当汽车出现转弯时,大部分算法都偏移到对面来的汽车灯光上,只有文中算法和PCA算法准确地对目标汽车进行了跟踪;在DavidIndoor视频中,目标人物从屋子黑暗角落走到明亮位置,同时伴有尺度变化和头部旋转.文中算法不仅能够适应跟踪目标的亮度变化,而且当目标人物存在角度变化时,也能较准确地进行跟踪.MIL算法虽然也对目标人物进行成功跟踪,但是不能随着目标尺度大小的变化而变化.Frag算法对光照变化比较敏感,所以存在跟丢现象.

图1(f)和(h)为David Outdoor和Stone视频.在David Outdoor视频中,存在背景混乱、遮挡以及目标人物旋转等干扰跟踪效果的因素.从跟踪结果来看,目标人物第1次经过树木遮挡,且当目标人物旋转时,只有文中算法准确地进行了跟踪,其他算法都跟踪失败;Stone视频存在严重的相似物体干扰,人物手部的颜色和目标石头的颜色以及背景石头的颜色非常相似,同时对目标石头存在遮挡.图1结果表明,文中算法对相似物体的干扰现象也有着非常鲁棒的性能,其他算法则容易受到干扰,跟踪失败.

3.2定量比较

文中采用中心位置误差(以像素为单位)和覆盖率两个指标对不同跟踪算法的性能进行比较.中心位置误差是指通过比较跟踪算法的跟踪方框的中心位置与人工手动标注的跟踪目标的中心位置之间的欧式距离得到的.覆盖率的含义,其中,表示第t帧中跟踪目标以为中心的方框的覆盖面积,表示第t帧中采用跟踪算法得到的以为中心的跟踪方框覆盖面积.很明显,OR值越大,表明跟踪算法的性能越好.为跟踪结果标准的中心位置,为采用跟踪算法得到的中心位置.图2给出了不同算法在各个帧的中心位置误差图,其中横坐标为帧号,纵坐标为中心位置误差.从图2中可以看出,文中算法的中心位置误差对给出的8种视频是最低的.图3给出了不同算法的覆盖率对比,相比其他算法,文中算法的跟踪目标覆盖率较高,能实现鲁棒的跟踪.

3.3计算复杂度分析

假设观测图像样本的维数为d,子空间基底U的秩为r,每一帧的迭代次数为n.根据文献[10]可知,文中算法每一帧的计算复杂度为O(drn+nr2+r3),若整个视频有F帧,则整个视频的跟踪复杂度为O((drn+nr2+r3)F).若采用标准RPCA算法进行视频跟踪,则迭代n次的复杂度为O(dtrn+nr2+r3),t为跟踪的视频帧数,完整视频的跟踪复杂度为O(d F2rn+Fnr2+Fr3),复杂度相对跟踪视频的帧数是呈二次平方增加的.

图3　覆盖率比较

4　结束语

文中提出了一种基于低秩特征的在线目标跟踪算法,把固定帧的视频看作是观测矩阵,当有新的视频流到来时,采用增广拉格朗日算法增量地求出观测矩阵的低秩特征,解决了传统RPCA方法不能在线处理大数据的缺点.相比其他算法,文中算法充分利用跟踪目标的全局子空间,并用低秩特征更新字典矩阵,解决了当跟踪结果出现遮挡时,字典更新出现偏差的问题.通过与其他6种算法对比,文中算法能够较好地克服视频中出现的遮挡、尺度变化、光照变化等问题,具有较强的鲁棒性.

[1]BABENKO B,YANG M H,BELONGIE S.Robust Object Tracking with Online Multiple Instance Learning[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(B):1619-1632.

[2]黄宏图,葛渊,张继,等.仿射变换在压缩感知跟踪中的应用[J].西安电子科技大学学报,2015,42(2):162-205. HUANG Hongtu,GE Yuan,ZHANG Ji,et al.Application of Affine Transform in Compressed Sensing Tracking[J]. Journal of Xidian University,2015,42(2):162-205.

[3]XUE M,LING H B.Robust Visual Tracking Using L1 Minimization[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision.Piscataway:IEEE,2009:1436-1443.

[4]贺文骅,刘志镜,屈鉴铭.利用超像素混合投票的在线目标跟踪算法[J].西安电子科技大学学报,2015,42(3): 61-66. HE Wenhua,LIU Zhijing,QU Jianming.Online Visual Tracking Method Based on Superpixel Hybrid Voting[J]. Journal of Xidian University,2015,42(3):61-66.

[5]ROSS D,LIM J,LIN R S,et al.Incremental Learning for Robust Visual Tracking[J].International Journal of Computer Vision,2008,77(1/2/3):125-141.

[6]王海军,张圣燕.基于L2范数和增量正交投影非负矩阵分解的目标跟踪算法[J].黑龙江大学自然科学学报,2015,32 (2):262-269. WANG Haijun,ZHANG Shengyan.Object Tracking Algorithm via L2 Norm and Incremental Orthogonal Projective Non-negative Matrix Factorization[J].Journal of Natrual Science of Heilongjiang University,2015,32(2):262-269.

[7]BAO C L,WU Y,LING H B,et al.Real Time Robust L1 Tracker Using Accelerated Proximal Gradient Approach[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington: IEEE,2012:1830-1837.

[8]WANG D,LU H C,YANG M H.Online Object Tracking with Sparse Prototypes[J].IEEE Transactions on Image Processing,2013,22(1):314-325.

[9]CANDÈS E,LI X D,MA Y,et al.Robust Principal Component Analysis?[J].Journal of the ACM,2011,58(3): 1-37.

[10]LIU G,LIN Z,YAN S,et al.Robust Recovery of Subspace Structures by Low-rank Representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(1):171-184.

[11]ZHANG C C,LIU R S,QIU T S,et al.Robust Visual Tracking via Incremental Low-rank Features Learning[J]. Neurocomputing,2014,131:237-247.

[12]LIN Z C,LIU R S,SU Z X.Linearized Alternating Direction Method with Adaptive Penalty for Low-rank Representation[C]//Advances in Neural Information Processing Systems:24.New York:NIPS,2011:612-620.

[13]ADAM A,RIVLIN E.Robust Fragments-based Tracking Using the Integral Histogram[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2006:798-805.

[14]ZDENEK K,MATAS J,MIKOLAJCZYK K.P-N Learning:Bootstrapping Binary Classifiers by Structural Constraints [C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2010: 49-56.

[15]KWON J,LEE K M.Visual Tracking Decomposition[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2010:1269-1276.

(编辑:齐淑娟)

Object tracking via online low rank representation

WANG Haijun1,2,GE Hongjuan1,ZH ANG Shengyan2
(1.College of Civil Aviation,Nanjing Univ.of Aeronautics and Astronautics,Nanjing 210016,China; 2.Key Lab.of Aviation Information Technology in Univ.of Shandong,Binzhou Univ.,Binzhou 256603,China)

Object tracking is an active research topic in computer vision.The traditional tracking methods based on the generative model are sensitive to noise and occlusion,which leads to the failure of tracking results.In order to solve this problem,the tracking results of the first few frames are used as the observation matrix,and the low rank features of the observation model are solved by the the RPCA model. When the new video streams come,a new incremental RPCA is proposed to compute the new observation matrix by the augmented Lagrangian algorithm.The tracking model is established in the Bayesian framework,and the dictionary matrix is updated with the low rank feature.We have tested the proposed algorithm and six state-of-the-art approaches on eight publicly available sequences.Experimental results show that the proposed method has a lower pixel center position error and a higher overlap ratio.

object tracking;low rank feature;RPCA model;dictionary matrix

TP391

A

1001-2400(2016)05-0098-07

10.3969/j.issn.1001-2400.2016.05.018

2015-09-07 网络出版时间:2015-12-10

山东省自然科学基金资助项目(ZR2015FL009);滨州市科技发展计划资助项目(2013ZC0103);滨州学院科研基金资助项目(BZXYG1524)

王海军(1980-),男,南京航空航天大学博士研究生,E-mail:whjlym@163.com.

网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.036.html