基于多层多位置稀疏的滑动轴承AE信号降噪
张峻宁, 张培林, 陈彦龙, 孙也尊, 杨望灿
(1.军械工程学院,七系 石家庄 050003; 2.驻二四七厂军事代表室,太原 030009)
基于多层多位置稀疏的滑动轴承AE信号降噪
张峻宁1, 张培林1, 陈彦龙1, 孙也尊2, 杨望灿1
(1.军械工程学院,七系 石家庄 050003; 2.驻二四七厂军事代表室,太原 030009)
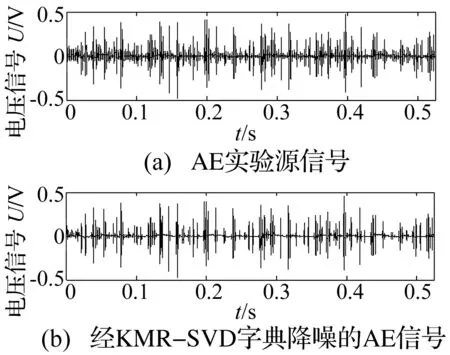
滑动轴承的声发射(Acoustic Emission, AE)信号噪声污染严重,限制了K均值奇异值分解(K-means Singular Value Decomposition,K-SVD)字典算法的降噪能力。基于此,结合AE信号特点,提出了基于多层多位置稀疏的滑动轴承AE信号降噪算法。首先提出移动标尺策略重构AE信号,使信号获得多层多位置的稀疏特性,解决了K-SVD容易忽略原子间隐藏信息的问题,然后通过灰色B型绝对关联度降低字典原子冗余度,提高字典运算速度。因此,与传统的K-SVD算法相比,该算法具有更好的降噪性能。应用到实例中,该算法成功获得了滑动轴承不同程度摩擦状态的变化,证明了该算法的有效性。
滑动轴承;声发射;K均值奇异值分解(K-SVD);移动标尺;灰色B型绝对关联度
滑动轴承的接触摩擦故障不像滚动轴承故障,没有明显的特征频率指向轴承损坏,因此监测滑动轴承的故障极为困难。近几年不少学者通过声发射(acoustic emission, AE)信号监测滑动轴承,但声发射信号易受到噪声的干扰,致使微弱故障的监测效果并不好,AE技术的发展一直受到噪声因素的制约。目前常用的降噪方法主要通过频率分布将信号和噪声分开,例如小波分解,默认高频为噪声、低频为信号,通过小波分解去除含噪声的高频部分,但噪声和信号的边界却只能依据经验公式;再者,机械信号中高频部分往往是故障特征提取的关键,因此选择小波对信号降噪并不是最佳。
信号的字典稀疏表示是当前研究的另一热点,字典中的原子代表信号的原始模型,信号具有被字典稀疏的特点;而噪声“杂乱无章”的排列决定了不具有字典稀疏的特性,因此字典降噪通过字典稀疏信号,避免了噪声与高频信号混淆问题,弥补了小波分解的不足,其中最经典算法是K-SVD。近几年,许多学者深入研究K-SVD算法并优化字典算法。例如,文献[1]针对图像降噪,提出了递归最小二乘字典学习算法(Recursive Least Squares Dictionary Learning Algorithm, RLS-DLA),相比于K-SVD提高了收敛速度,但信噪比却仅提高了1 dB。而后,发展了如基于聚类的局部字典学习算法(clustering-based denoising with locally lerrned dictionary,K-LLD)[2],最小二乘字典学习算法(Least Squares Dictionary Learning Algorithm, LS-DLA)[3,4],奇异值分解降噪字典算法(K-means Singular Value Decomposition Denoising,K-SVDD)[5,6],K均值聚类-奇异值分解的字典算法(K-means Singular Value Decomposition Dictionary Learning Algorithm, KSVD-DLA)[7,8]等,针对图像信号降噪都取得了良好的效果,但直接应用于AE信号降噪效果不佳。究其原因,AE信号属脉冲信号类一维信号,简单通过字典整体稀疏,易忽略原子间隐藏的脉冲结构特征。
本文在K-SVD的基础上,提出移动标尺策略重构信号,试图对AE信号多层多位置稀疏,实现降噪最大化的同时保留信号的特征信息;为了提高字典运算速度,应用灰色B型绝对关联度(Absolute Grey Relational Degree of B-mode,AGRDB)[9]去除冗余字典原子,降低字典维数。实验结果表明,该算法不仅具有更好的降噪效果,更好的保留信号特征信息,而且具有较快的运算速度。
1 AE信号的多层多位置K-SVD字典
1.1 信号的K-SVD字典
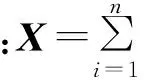
argmin(‖a‖0),s.t.X=Da
(1)
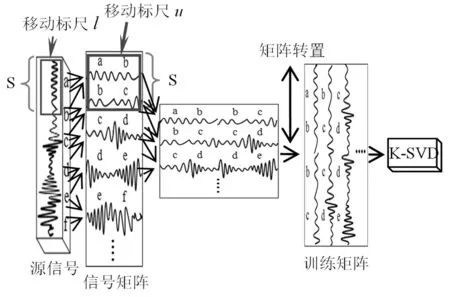
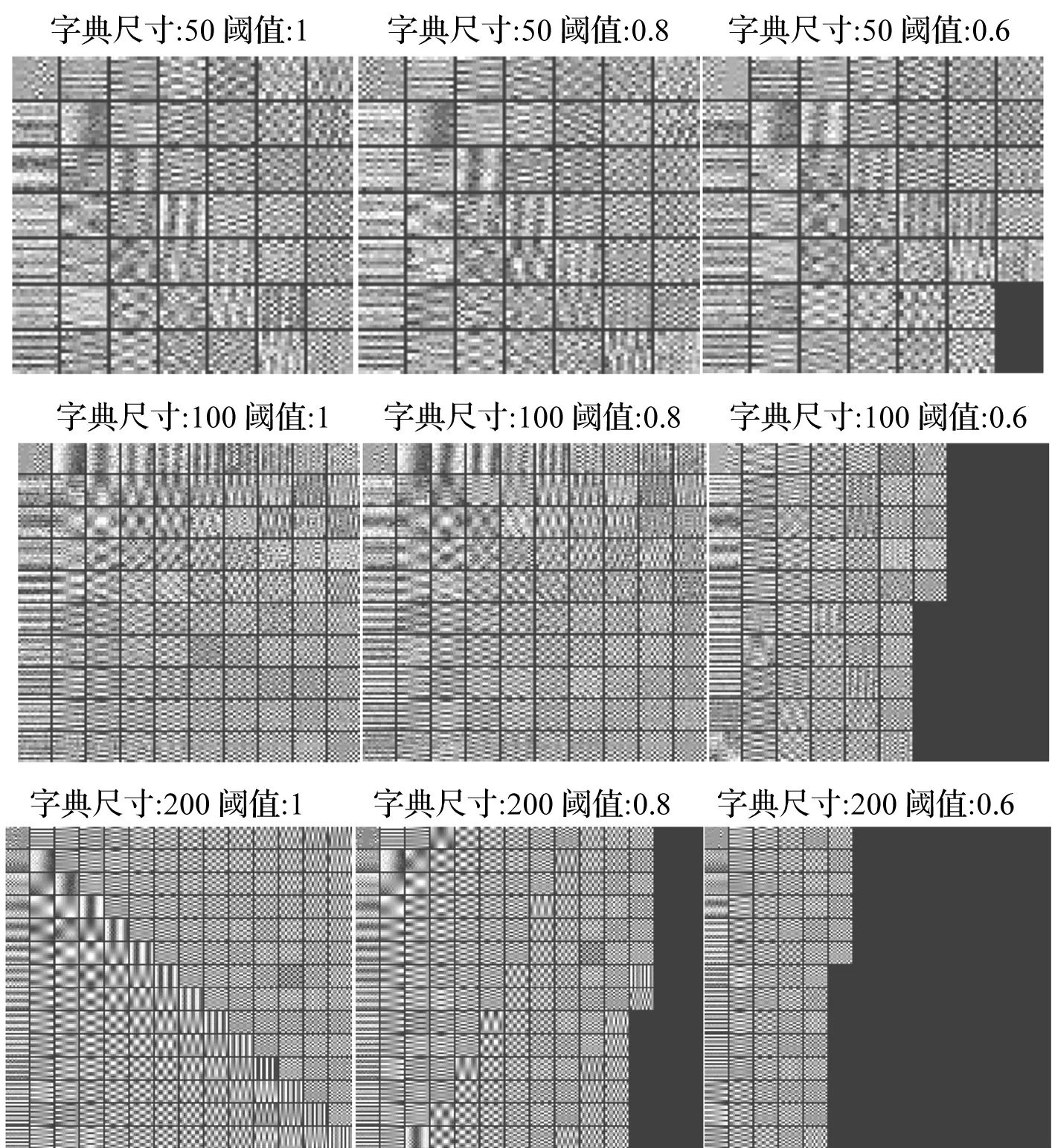
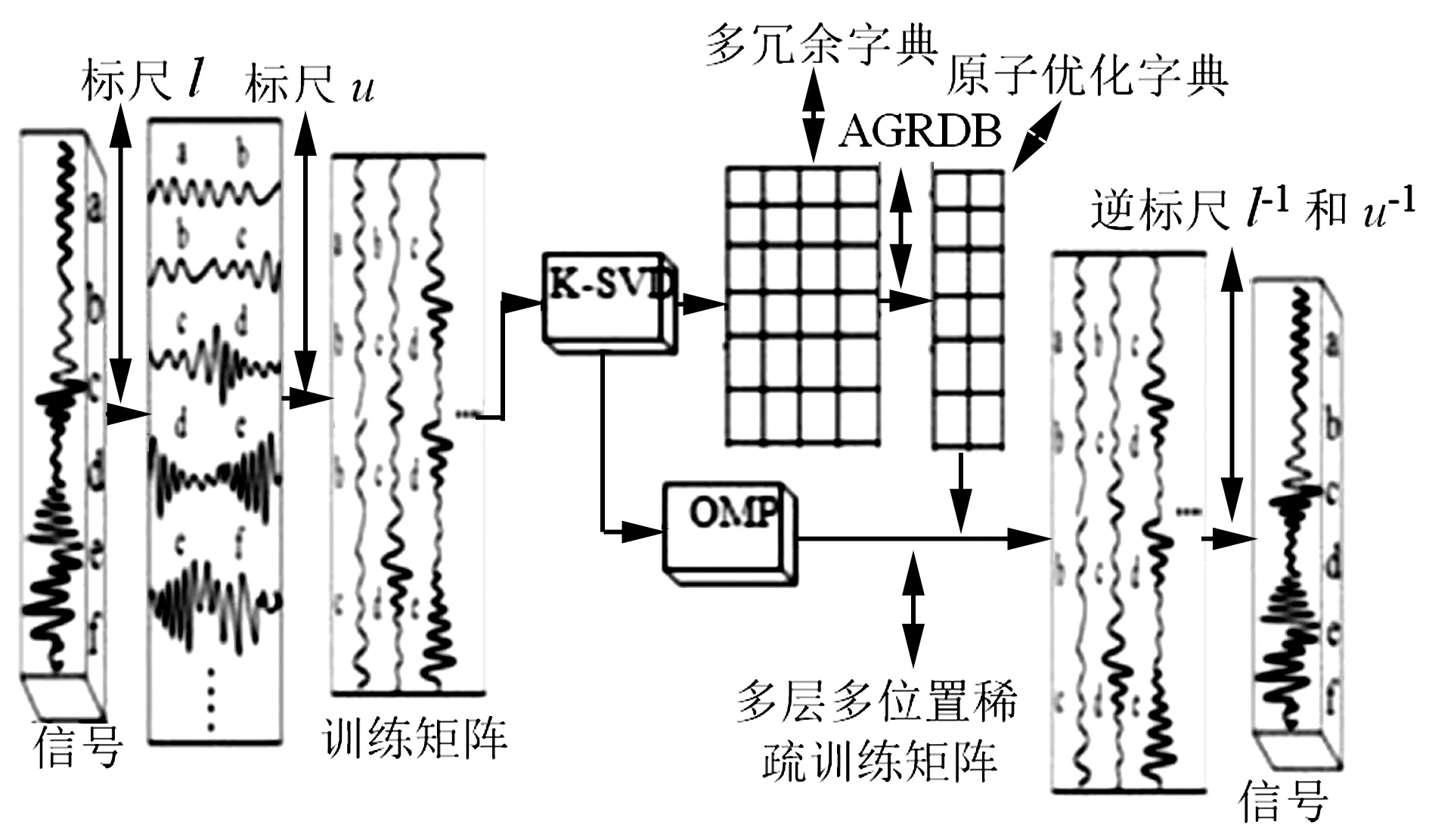
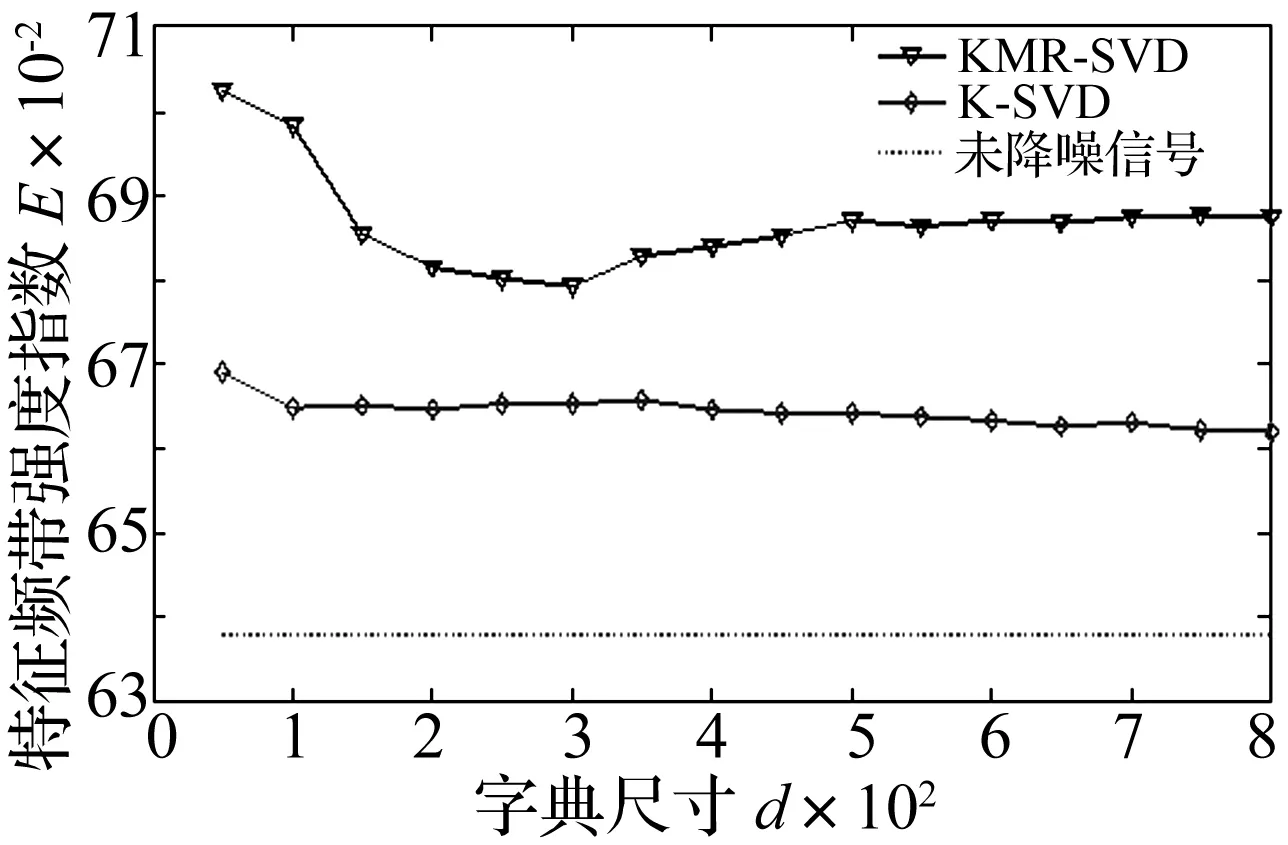
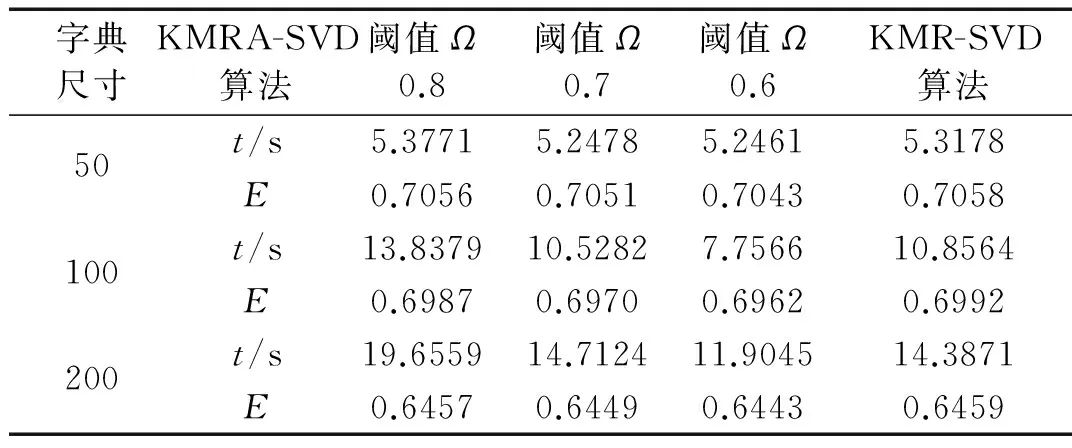
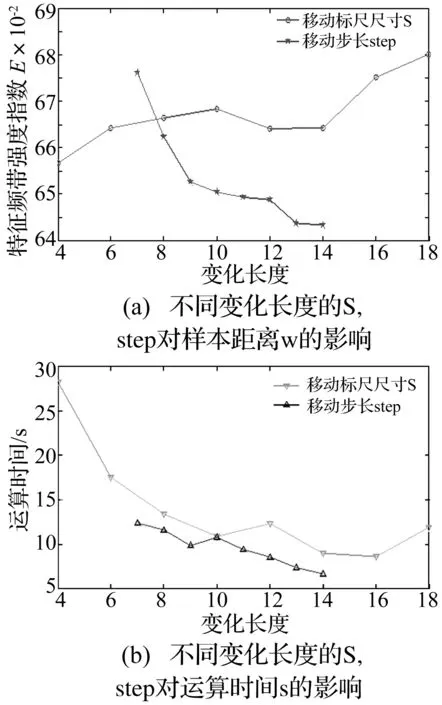
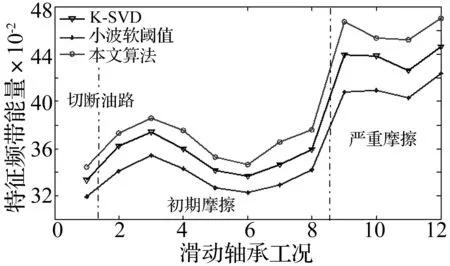
式中:D∈Rn×m为构造的字典矩阵,a∈Rm是字典矩阵的稀疏向量,‖a‖0 假定含噪的AE信号为Y=X+B,其中X是AE信号,B是均值为零,方差为σ2的随机白噪声。若X能被字典D表示,X=Da,则AE信号的降噪稀疏为: (2) 由式(2)知,信号稀疏的效果仅取决于字典矩阵D中少数原子,但是AE信号数据量大,且K-SVD中初始化的DCT字典前后行系数差距大,仅仅通过字典原子单尺度稀疏AE信号,容易造成去噪不彻底和部分信号特征信息遗漏的问题。 1.2 多层多位置的移动标尺策略 基于上述分析,本文尝试寻找一种“放大镜”,通过放大镜研究观测镜中所呈现的数据,隐藏在原子中的细微信息就能被放大和提取。因此,本文提出移动标尺字典算法(K-means singular value decomposition dictionary-with sliding ruler,KMR-SVD),利用标尺将每一段信号存储于不同列向量的不同位置,整个AE信号组成为交替重叠的矩阵信号;再被字典稀疏,就可实现多层多位置稀疏AE信号,避免原子间特征信息的遗漏,达到最优降噪的目的。下文给出KMR-SVD的具体步骤和算法框架图。 (1)记L为移动标尺l,Lj=L(S)为移动标尺算子,用该标尺截取训练信号X∈RG。截取规则为:用长为S的标尺截取X的首段信号,组成信号向量L1,并移动标尺距离step(step (2)记U为移动标尺u,用Uj=U[S,S]的标尺依次抽取大小为(S×S)的块状矩阵UjMx,定义j(1≤j≤t-S+1)为块状矩阵抽取的列数标记,然后再把每一块拉直作为一个向量Ij,并全部组成训练矩阵UMx=(I1,I2,…,It-S+1)。 (3)定义字典大小为N,噪声增益为P,按照K-SVD算法求解每列向量Ij稀疏系数: argmin{μ‖Y-X‖+ (3) 式中:λj为惩罚因子,μ为拉格朗日算子。 图1 KMR-SVD算法框架图Fig.1 Diagram of KMR-SVD algorithm 如图1所示,移动标尺策略将AE信号分段交替重组,以c段信号为例,通过标尺将c段信号存储于训练矩阵的前S列向量中的不同位置,这样矩阵中不同列向量间必然有交叉,这部分交叉将导致采用更多的向量来描述,从而更精确的表达信息,弥补了K-SVD中DCT字典系数分布不一致的缺点。因此,多次稀疏的信号去噪效果更好,特征信息的稀疏更加完全。 采用移动标尺策略重构AE信号,获得多层多位置的稀疏特性,将具有更好的降噪效果,但却付出了信号数据量增加、字典冗余度高,降低了稀疏效率的代价。AGRDB是一种描述两者事物在空间结构相似性的方法,广泛应用于各个行业,尤其在人脸识别、指纹鉴定等领域。本文试图依据这种在空间结构的相似性解决字典原子高冗余问题,将AGRDB引用到KMR-SVD字典算法中,提高字典运算速度,并将该算法称为基于多层多位置的K-SVD快速字典算法(K-means singular value decomposition dictionary-with mobile ruler and absolute grey relational degree of B-mode,KMRA-SVD)。因只考虑原子间的关联度,仅定义列向量的AGRDB。 (4) 式中:δmn是字典原子dm、dn之间的AGRDB值,d:m、d:n为字典第m,n列的原子。 (5) (1)将向量d:m和d:n始点均差化。 (6) δmn= (7) 式中:距离差(位移差Dmn,速度差Vmn,加速度差Amn)如下表示。 (8) (9) (10) 分析式(9)可知,AGRDB是以两原子之间空间结构的相似性为依据,刻画原子间的关联度δmn。关联度越大,表明两原子抗噪性能越接近。因此设定阈值Ω,认定当两原子的关联度δmn≥Ω时,两原子为同一类原子,在更新字典阶段,只需取其中一个原子作为该类原子的类型。图2是在不同字典尺寸不同阈值下的KMRA-SVD字典原子,其中KMRA-SVD字典参数随机设定为:S=14,step=6,t=10,P=1.15,trainnum=1 000,噪声水平q=30,初始冗余字典DCT,稀疏度k=3。分析图2可见,字典的尺寸越大,字典原子冗余度越高,设置阈值的意义就越明显,且随着阈值Ω的减小,字典维数降低,字典运算的速度越快。 图2 不同字典尺寸不同阈值的KMRA-SVD字典原子Fig.2 KMRA-SVD dictionary atoms of different sizes and different threshold values 本文针对AE信号提出了多层多位置稀疏的移动标尺策略,同时引入AGRDB优化KMR-SVD字典原子,降低了字典原子冗余度,提高了降噪效果和稀疏表示的效率。下面给出KMRA-SVD字典快速算法框架图(见图3)和具体步骤。 图3 KMRA-SVD字典算法框架图Fig.3 KMRA-SVD algorithm frames dictionary 1)信号重组:按照1.1节建立移动标尺l和u,通过该标尺得到训练矩阵UMx; 2)字典更新:初始化字典D=overcomplete DCT字典,并利用K-SVD初步完成更新字典各列原子j=1,2,…,N,再按照式(5)~(11)依次计算第n列原子与第m列原子的关联度δmn(m 3)系数稀疏编码:因字典D已知,系数aj和信号向量UjMx的求解通过OMP(Orthonormal Matching Pursuit)[10-11]算法不断迭代得到: aj=argmin‖aj‖0, (11) 4)AE信号恢复:利用移动逆标尺u-1和l-1(与标尺u,l的构建顺序相反)将稀疏后的UMx矩阵恢复成AE信号,而对于不同列不同位置稀疏的相同信号,再通过求取平均值作为该信号的最终AE信号,就避免原子间特征信息的遗漏,达到最优降噪的目的。 采集了滑动轴承摩擦故障实验的声发射数据验证本文算法的有效性,主要做了三方面研究。①比较了K-SVD、KMR-SVD字典算法在AE信号的降噪效果,讨论移动标尺策略的作用;②测量了KMR-SVD、KMRA-SVD字典降噪的运算时间,分析AGRDB在字典维数降低和对降噪质量的影响以及字典参数[step,S]与降噪的关系;③利用经KMRA-SVD算法降噪的AE信号监测内燃机滑动轴承,验证KMRA-SVD算法相比于小波,更好保留微弱信号特征信息的优势。 实验数据来源于西南交通大学机械试验台的S195-2型柴油机,声发射传感器安置于柴油机输出端主轴承座附近的机体壁上,实验模拟工况2 000r/min,工率4.67 kW,实验通过切断润滑油油路模拟滑动轴承摩擦故障,同时测定轴承背面温度,作为判断轴承是否出现故障的依据。规定开始切断油路为0时刻,断油前为“负”时刻,断油后为“正”时刻,具体工况见表1所示。 表1 故障发生前后滑动轴承工况特征的变化 4.1 K-SVD和KMR-SVD的降噪质量比较 随机设定KMR-SVD字典参数(S=14,step=6,t=1,P=1.15,trainnum=1 000,k=3,噪声水平q=30),并对实验信号降噪见图4所示。易见,经KMR-SVD降噪的信号效果明显,局部特征清晰。为了定量比较K-SVD和KMR-SVD的降噪效果,定义特征频段信号强度指数[12],设定Hi,i=1,2,3,…,2n为n层小波包分解中各频带能量值,H(p~q)为反映滑动轴承接触摩擦故障特征频带(p~q)的能量值。 (12) 易见,特征频带强度指数E反应了滑动轴承特征频带能量占整个频带的比重,E越大,则特征频带越显著,信号中的噪声和干扰信息越少。 针对本次实验,选择n=4层小波包分解,并根据文献[13]中高频信号能量变化是反应滑动轴承接触摩擦故障的重要特征的结论,定义高频频带9(50~56.25 kHz)~频带10(56.25~62.5 kHz)为特征频带。图5是信号在KMR-SVD和K-SVD字典降噪后的特征频带强度指数曲线,其中K-SVD字典相关参数(S=14,t=1,P=1.15,trainnum=1 000,冗余度为8)。分析曲线可得,KMR-SVD和K-SVD字典能够在一定程度对信号降噪,不同的是KMR-SVD字典降噪的特征频带强度指数均要高于K-SVD字典,表明了经KMR-SVD降噪的信号故障频带特征更加明显,去除噪声更加彻底,证明了移动标尺策略的有效性。 图4 KMR-SVD字典降噪效果图Fig.4 KMR-SVD dictionary noise reduction effect 图5 KMR-SVD和K-SVD的特征频带强度指数曲线Fig.5 The features band intensity index curves of KMR-SVD and K-SVD dictionary 4.2 KMRA-SVD和KMR-SVD的降噪速率比较 比较了KMRA-SVD和KMR-SVD对4.1节中AE源信号降噪的运算时间time和特征频带强度指数E,如表2所示。实验环境为:Intel core i5,2.40 GHz,内存4.00 GB,操作系统和软件为64位的win7的MATLAB (R2012b)。 表2 KMRA-SVD和KMR-SVD运算时间和特征频带强度指数的比较 经上表分析,字典尺寸越大,阈值Ω设定越小,KMRA-SVD运算的速度提高越快,表明通过AGRDB提高KMR-SVD字典运算速率的方法是有效的,但是随着阈值的降低,特征频带强度指数E逐渐减小,信号降噪效果越差,更进一步表明同时寻求降噪速率和降噪质量最大化的状态是不存在的,KMRA-SVD字典的推广,只能是降噪符合标准的前提下达到最快时间,或者运算时间要求下寻求最好的降噪质量。因此,认定阈值Ω为0.7时,KMRA-SVD算法在运算时间和降噪质量上效果不错。 为了进一步提高KMRA-SVD运算速率,分析了KMRA-SVD参数(S,step)对降噪的影响。图6是不同移动标尺参数(S,step)对KMRA-SVD的降噪质量和降噪时间的关系曲线。 图6 标尺参数(step、S)对降噪的影响Fig.6 Scale parameter impact on the noise reduction 从图6可见,标尺参数均能不同程度的影响降噪的质量和速度,例如移动步长step,微小变化都大幅决定了降噪的特征频带强度指数E,但却微小的影响运算时间;而移动标尺尺寸S则是呈现相反的变化。由此,KMRA-SVD字典的最佳降噪应是由最优参数和最佳字典共同完成,这也是未来的研究重点。 4.3 KMRA-SVD在滑动轴承AE信号上的应用 图7 不同滑动轴承摩擦工况的特征频带能量变化Fig.7Characteristics band energy of different bearing friction conditions 分析曲线发现,特征频带能量在摩擦早期逐渐增加,表明切断油路后,轴瓦开始形成点对点式接触摩擦;而后,轴瓦的凹凸被磨平,接触摩擦缓和,轴承处于短暂的润滑状态,因此频带能量又有所降低,这也是曲线呈波浪形增加的原因。如此波浪式发展,点对点式的接触摩擦逐渐发展成点对面式、面对面式的接触,直至最后轴承损坏,上述的变化正好符合摩擦是周而复始的恶性循环而逐渐摩擦越来越严重的摩擦学规律[14-15]。对比经K-SVD、小波软阈值降噪的信号频带能量图,也能分析上述特征。不同的是,通过本文算法去噪后的特征频带能量曲线更加突出,更好的保留微弱故障信息,证明了KMRA-SVD字典降噪的优势,因此针对混叠在AE信号中的噪声,利用KMRA-SVD字典算法降噪的方法是有效的。 基于多层多位置稀疏的K-SVD字典快速算法实现了对AE信号的降噪,该算法比经典字典算法K-SVD具有更好的降噪性能。提出移动标尺策略达到了AE信号多方向多位置稀疏的目的,提高了降噪的质量,然后通过AGRDB降低字典原子的冗余度减少了字典算法的运算时间。将该算法运用于滑动轴承AE信号分析,成功描述了滑动轴承不同状态之间的变化,准确检测了滑动轴承运行状态,完成了故障诊断。 [1] SKRETTING K, ENGAN K. Recursive least squares dictionary learning algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(4): 2121-2123. [2] CHATTERJEEPP, MILANFARP P. Clustering-based denoising with lo-cally learned dictionaries[J]. IEEE Trans on Image Pro-cessing,2009,18(7):1444-1451. [3] ENGAN K, SKRETTING K, HUSOY H J. Family of iterative LS-based dictionary learning algorithms, ILS-DLA, for sparse sig-nal representation[J]. DigitalSignal Processing,2007,17(1):38-49. [4] OLSHAUSEN B A, FIELD D J. Sparse coding of sensory inputs [J]. Current opinion in Neurobiology, 2004, 14(4): 481-487. [5] SMITH E C, LEWICKI M S. Efficient auditory coding [J]. Nature, 2006, 439(7079): 978-982. [6] ELAD M, ABARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745. [7] WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation [J]. Pattern Analysis and Machine Intelligence IEEE Transactions on,2009,31(2): 210-227. [8] AHARON M, ELAD M, BRUCKSTEIN A, et al. K-SVD: an algorithm for designing of overcomplete dictionaries for sparse representation[J]. IEEE Trans. on Signal Processing,2006,54(11): 4315-4320. [9] 邵晓刚. 基于矩阵灰色B型绝对关联度的人脸检测算法研究[D]. 辽宁: 东北师范大学, 2012. [10] GRIBONVAL R,NIELSEN M.Sparse approximations in signal and image processing[J].Signal Processing,2006,86(3):414-415. [11] 唐宏宾, 吴运新, 滑广军,等. 基于EMD包络谱分析的液压泵故障诊断方法[J].振动与冲击, 2012, 31(9):44-46. TANG Hongbin, WU Yunxin, HUA Guangjun. Fault diagnosis of pump using EMD and envelope spectrum analysis[J]. Journal of Vibration and Shock, 2012, 31(9):44-46. [12] YIN Chun, ZHONG Shouming, CHEN Wufan. Design of sliding mode controller for a class of fractional-order chaotic systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2012,17(1):356-366. [13] 荆双喜, 吴鑫涛, 华伟. 基于小波包频带能量特征提取的低速重载滑动轴承诊断研究[J]. 煤矿机械, 2007, 28(9):191-193. JING Shuangxi, WU Xintao, HUA Wei. Plain bearing fault diagnose based on detecting technology of wavelet packet frequency bandenergy[J]. Coal Mine Machinery, 2007,28(9): 191-193. [14] 傅和品, 秦萍. 滑动轴承故障诊断方法的实用性分析研究[J]. 轻工机械, 2006, 24(4): 97-98. FU Hepin, QIN Ping. The study of fault diagnosis method on slide bearing[J]. Light Industry Machinery, 2006, 24(4): 97-98. [15] 赵慧敏,梅建民,肖云魁,等.基于双谱和变精度粗糙集理论的柴油机故障特征自动提取[J].振振动与冲击, 2011,30(6):223-225. ZHAO Huimin, MEI Jianmin, XIAO Yunkui, et al. Automatic extraction of fault features for diesel engine based on bispectrum approach and variable precision rough set theory [J]. Journal of Vibration and Shock, 2011,30(6):223-225. De-noising approach for AE signals of plain bearings based on multi-level and multi-position sparse representations ZHANG Junning1,ZHANG Peilin1,CHEN Yanlong1,SUN Yezun2,YANG Wangcan1 (1. Department 7th Ordnance Engineering College, Shijiazhuang 050003, China;2. Military Delegation Office at Factory 247, Taiyuan 030009, China) Acoustic emission (AE) signals of plain bearings are polluted seriously by noise, this restricts the denoising capacity of the K-means singular value decomposition (K-SVD) dictionary algorithm. Here, a method for de-noising AE signals of plain bearings based on multi-level and multi-position spare representation was proposed considering the characteristics of AE signals. Firstly, AE signals’ multi-level and multi-position sparse characteristics were obtained by using the moving ruler strategy to reconstruct AE signals. Thus, the problem that the K-SVD ignored the hidden information among atoms was solved. Secondly, the computing speed of the dictionary algorithm was improved by applying the absolute grey relational degree of B-mode(AGRDB) to reduce the redunancy of atoms. Therefore, compared with the traditional K-SVD algorithm, it was shown that this proposed algorithm has a better denoising performance; moreover, it can preserve the information of local features as well. The examples’ results showed that the changes of the friction states of plain bearings are acquired with the proposed algorithm, and the effectiveness of the algorithm is verified. plain bearing; acoustic emission (AE); K-means singular value decomposition (K-SVD); moving ruler; absolute grey relational degree of B-mode 国家自然科学基金项目(51205405;51305454) 2015-05-14 修改稿收到日期:2015-09-25 张峻宁 男,硕士生,1992年生 张培林 男,教授,博士生导师,1955年生 TH133.31 A 10.13465/j.cnki.jvs.2016.19.018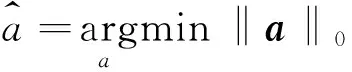
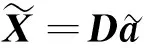
2 KMR-SVD字典原子冗余度的降低
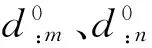
3 KMRA-SVD字典算法框架
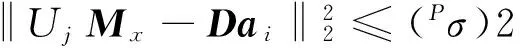
4 KMRA-SVD的验证与应用

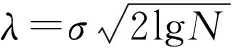
5 结 论

