考虑温度效应的圆形均布载荷下沥青混凝土场坪的动力响应分析

张震东， 马大为， 杨 云， 何 强

(1.南京理工大学 机械工程学院，南京 210094； 2.黄河科技学院 交通学院，郑州 450000)



考虑温度效应的圆形均布载荷下沥青混凝土场坪的动力响应分析

张震东1， 马大为1， 杨 云2， 何 强1

(1.南京理工大学 机械工程学院，南京 210094； 2.黄河科技学院 交通学院，郑州 450000)

对黏弹性材料的积分型本构关系进行Laplace积分变换，推导出采用广义Maxwell模型描述的黏弹性算子，并引入“时温等效”原理来反映温度对沥青混凝土力学性能的影响。将直角坐标系下黏弹性问题的动力平衡方程、几何方程以及物理方程进行Laplace变换和二维Fourier变换，建立了多层黏弹性体系的传递关系。在此基础上，根据已知边界条件给出了场坪表面垂向位移的求解方法，并利用Matlab软件编写计算程序。以三层沥青混凝土场坪为例，分析了考虑温度效应的圆形均布动载荷下场坪的动力响应。结果表明，温度越高，场坪下沉量越大，局部弯沉现象越明显，残余变形也愈大。

温度效应；黏弹性；沥青混凝土场坪；传递矩阵；动力响应

沥青路面的一种重要军事用途，就是作为导弹发射车辆的发射场坪，发射装备主要通过圆形刚性支撑盘将载荷传递至发射场坪表面，表面的下沉又会影响发射装备的动力响应，最终影响到导弹的出筒姿态，因此，研究沥青场坪的动力响应具有重要的工程意义。

沥青混凝土场坪的动力响应问题已经进行了较多研究，研究方法主要有弹性/黏弹性层状理论，地基上的板梁理论以及有限元方法。由于弹性/黏弹性层状理论是根据路面的实际结构建立起来的，而且一般情况下可得到理论解，因此在道路工程领域广泛应用。传递矩阵法求解弹性/黏弹性层状体系问题时，具有概念清晰、便于工程应用的特点，任瑞波等[1-2]利用传递矩阵方法，分析了多层黏弹性半空间体在动载荷作用下的动力响应；上述研究由于在柱坐标系下采用Hankel积分变换求解状态方程，解决轴对称问题时优势明显。为了使传递矩阵方法能够得到更广泛的应用，王有凯等[3-4]发展了直角坐标系下层状弹性体系的传递矩阵技术，不足之处在于只解决了静力学问题。汤连生[5]在弹性层状体系理论基础上，采用传递矩阵方法，结合黏弹性运动方程，推导了交通荷载下三维黏弹性层状道路系统的动力响应解答，但没有很好的描述沥青混合料的黏弹特性。董忠红等[6-7]将沥青路面视为层状体系结构，采用Burgers模型表征面层的黏弹性行为，建立了移动荷载下路面的动力响应模型。

众所周知，温度对黏弹性材料的力学性能有很大影响，而上述文献均忽略了温度效应，虽然艾智勇在文献[8]中引入温度场，得到了稳定温度场下层状路面体系平面问题的解析层元解，但仍然没有考虑沥青混合料的热敏感性。

在地基上的板梁理论方面：刘小云等[9-10]将沥青路面简化为非线性黏弹性地基上的黏弹性无限长梁，分析了车辆荷载下路面的动力响应。卢正等[11-12]将路面视为黏弹性地基上多层Kirchhoff薄板，解决了考虑车-路耦合的路面动力学问题，然而无论是梁模型，还是板模型都存在一些假设，计算精度不高。相比之下有限元法比较精确，在道路工程中应用较多，赵延庆[13]建立了典型沥青路面的三维动态有限元模型，阐述了温度、阻尼等因素对路表弯沉的影响规律。张丽娟[14]同样基于有限元方法，采用广义Maxwell模型描述黏弹性材料的变形模式，计算蠕变应变和弹性应变，分析了沥青混合料的弹性恢复能力。周晓和[15]采用有限元方法分析了某导弹无依托发射场坪的动力响应。文献[13-15]主要利用ABAQUS、ANSYS等成熟的有限元软件进行响应分析，虽然结果比较直观，但偏重于利用有限元软件自身的本构模型进行多工况计算，总结分析场坪动力响应规律，对机理研究相对较少。

针对现有研究存在的不足，本文采用广义Maxwell黏弹性模型，结合“时温等效”原理考虑了温度对沥青混合料力学性能的影响，采用传递矩阵方法求解直角坐标系下的多层黏弹性半空间问题，进一步完善了沥青场坪动力响应的研究工作。

1 黏弹性模型

1.1 黏弹性算子

黏弹性材料的积分型本构方程为：

(1)

式中:σ(T,t)为应力；T为温度；t为时间；K(T,t)为松弛模量；ε(T,t)为应变。

采用卷积形式表示，式(1)可写成：

σ(T,t)=K(T,t)*dε(T,t)

(2)

式中:*为卷积运算符号。

定义如下形式的Laplace变换对：

(3)

式中:s为复变量。

对式(2)进行Laplace变换，并利用斯蒂尔吉斯卷积的性质，上式可表示为：

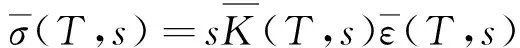
(4)

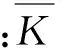
由式(4)可得Laplace变换后的黏弹性算子：

(5)

1.2 广义Maxwell模型及“时温”等效原理

由M个Maxwell体并联组成的广义模型，可以解释复杂的应力松弛现象[14]，其松弛模量为：

(6)

Km(T)为第m个Maxwell单元的弹性模量，τm=ηm/Km为松弛时间，ηm(T)为第m个Maxwell单元的黏性常数。

根据“时温等效”原理，某一温度条件下的应力松弛过程，可以用不同温度条件下的模量-时间曲线拟合而得。“时温等效”原理可表示为：

K(T,t)=K(T0,t/αT)

(7)

式中:T0为参考温度，αT为位移因子。

本文采用Arrhenius公式确定位移因子αT[16]：

αT=exp[δH(1/T-1/T0)/R]

(8)

式中:δH为材料活化能，R为摩尔气体常数。

(9)

2 多层体系的传递关系

本文在直角坐标系中对多层黏弹性体的轴对称问题进行分析，假设x,y方向场坪尺寸足够大，如图2所示。

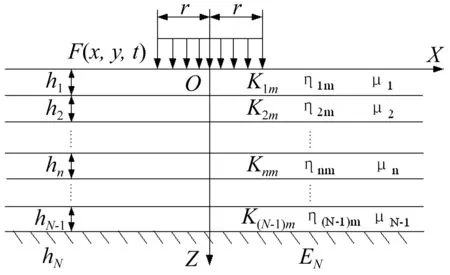
图1 多层黏弹性体系Fig.1 Multilayered viscoelastic body

2.1 黏弹性问题的基本方程

不计体力时，直角坐标系下黏弹性问题的基本方程包括动力平衡方程、几何方程及物理方程，分别对上述三个方程进行Laplace变换，可得到：

① 动力平衡方程

(10)

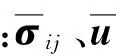
② 几何方程

(11)

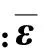
③ 物理方程

(12)

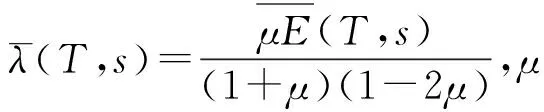
2.2 单层体系的传递关系

定义如下变量：

(13)

由式(10)～(13)整理得到：

(14)

定义二维Fourier变换对，如下：

(15)

式中:ξ，ζ为复变量。

对式(14)进行二维Fourier变换，得到：

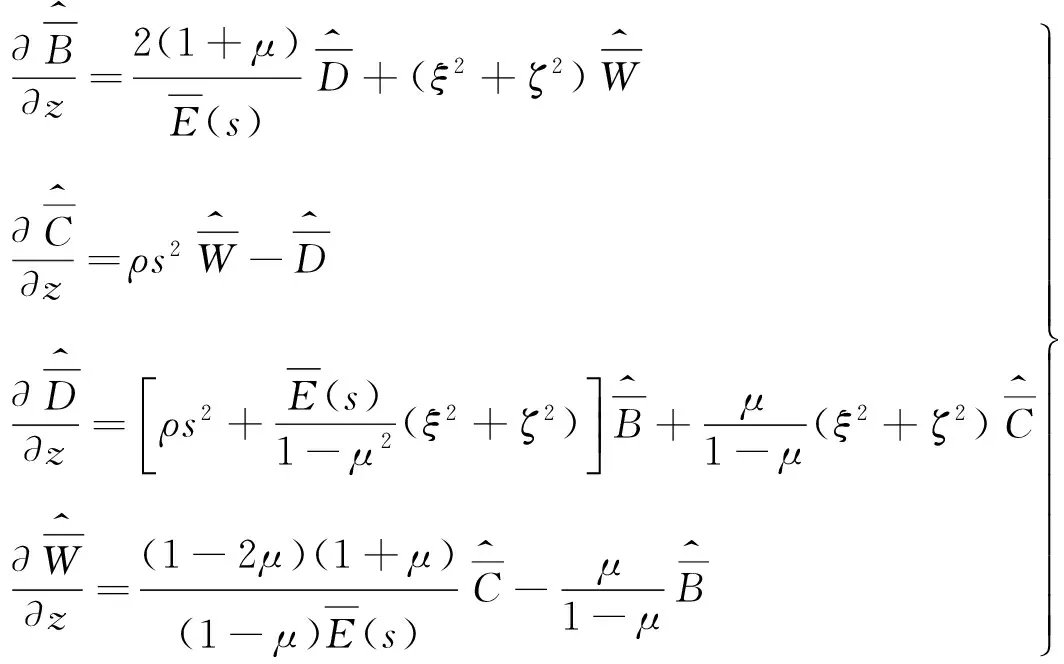
将式(16)写成矩阵形式：

(17)

式中:

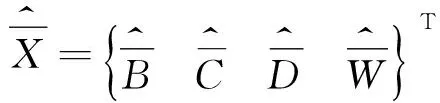
式(17)给出了单层状态变量的传递关系。

2.3 多层体系传递矩阵求解

根据文献[3]，式(17)解的形式为：

(18)

式中：eAnz为指数传递矩阵，上式给出了z= 0处经拉氏变换以及二维傅氏变换的位移和应力边界向量与任意深度z处向量之间的关系。

eAnz可用下式求出：

Tn=eAnz=L-1{[pI-An]-1}

(19)

式中:p为对z进行Laplace变换后的复变量，由式(19)可求得场坪各层的传递矩阵Tn。

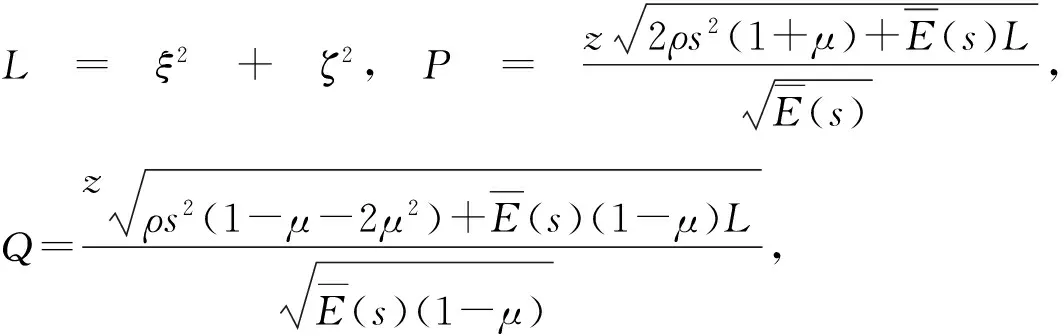
Tn24=

假设层间状态完全连续，通过逐层传递，可得到多层黏弹性体系的传递关系：

(20)

式中:hn为第n层的厚度。

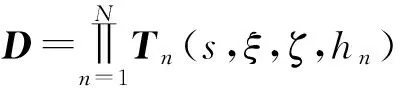
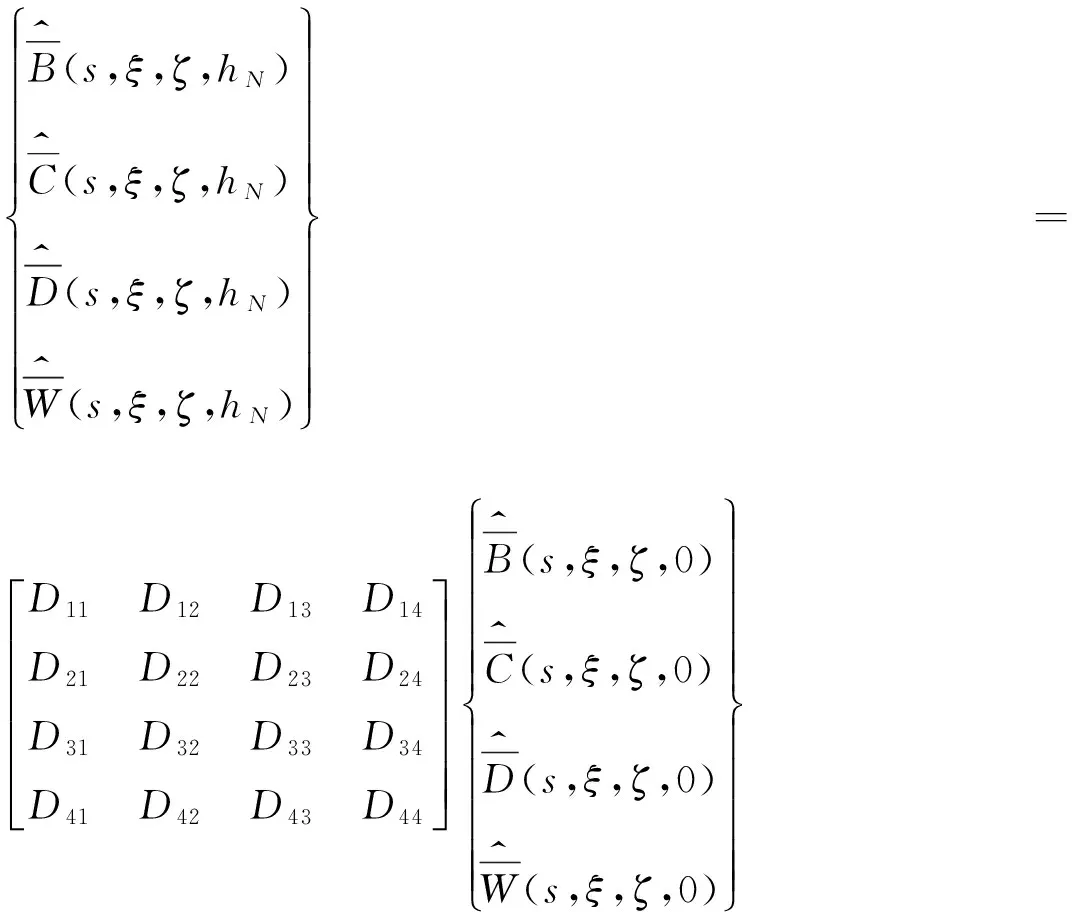
3 场坪表面下沉量求解

场坪表面的圆形均布动载荷可表示为：

F(x,y,t)=f(t)×H[r2-(x2+y2)]

(22)

式中:f(t)为载荷平均集度，本文取载荷平均集度变化规律为f(t)=0.7×sinπt，单位为MPa.s；r为载荷圆形分布区域半径；H(x,y)为Heaviside阶跃函数。

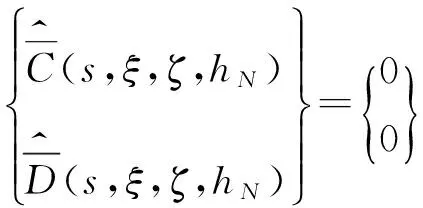
由边界条件，以及式(21)可得到：

对上式进行Laplace逆变换后再进行二维Fourier逆变换就可求出场坪表面的垂向位移。

4 算例及结果分析

本文视基层与土基为弹性体，以3层沥青混凝土场坪为例(如图2)分析温度对路表弯沉的影响，参数取值见表1。参考文献[16]，黏弹性模型参数取值如表2。

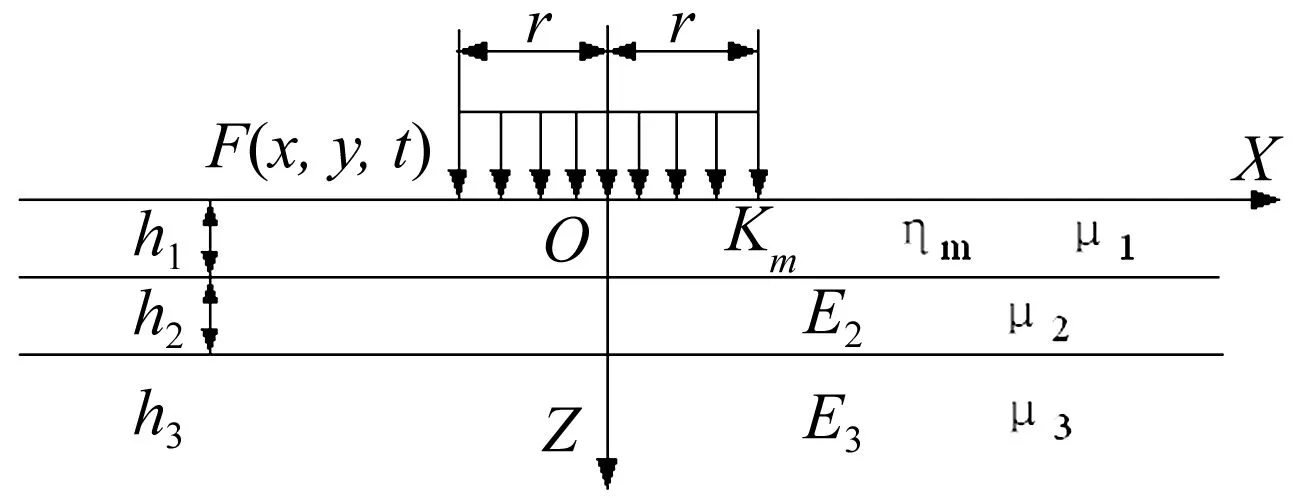
图2 三层沥青混凝土场坪Fig.2 Three layered asphalt launching site viscoelastic body

参数符号参数名称取值ρ1ρ2ρ3面层、基层、土基密度/(kg·m-3) 200020001900h1h2h3面层、基层、土基厚度/m0.18 0.35∞E2E3基层、土基弹性模量/MPa910 100μ1μ2μ3面层、基层、土基泊松比0.40.25 0.25r载荷作用面半径/m0.1065T0参考温度/K268

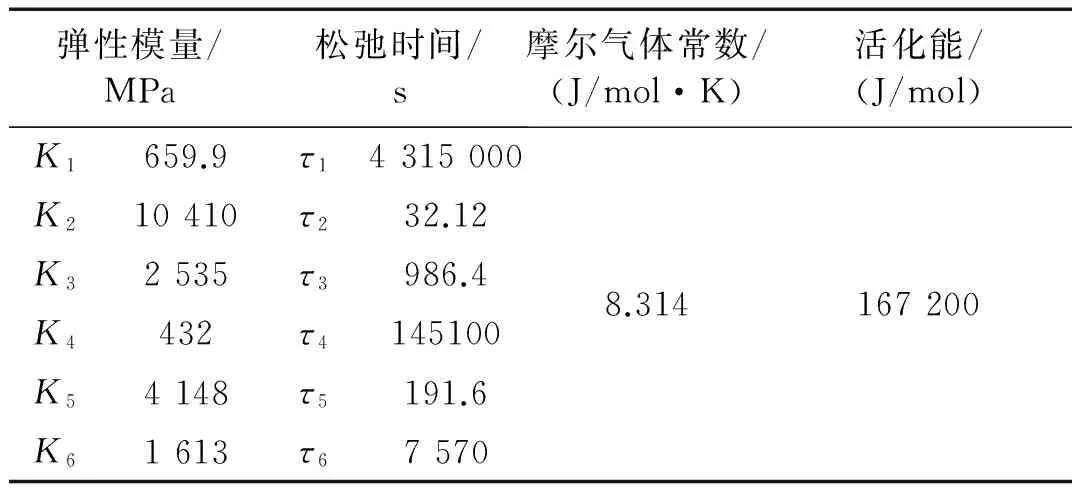
表2 Maxwell模型参数

本文取载荷作用时间为1 s，载荷完全卸载后观测场坪表面的弹性恢复情况。采用DURBIN F方法[17]进行Laplace逆变换，参考10节点的复合二维Guass积分方法[4]处理Fourier逆变换，在MATLAB软件中编写计算程序，可得到时域下直角坐标系中场坪表面的下沉量。

图3给出了不同温度时，载荷作用面中心处的下沉量变化曲线。通过这组曲线可以看出，当面层温度从0℃升高至60℃时，沥青混合料黏性越明显，路面面层刚度下降，引起场坪表面下沉量逐渐增大。另外，面层温度为0℃时，载荷卸载后路表弯沉能够马上恢复，说明温度较低时沥青混合料的黏弹特性可忽略。

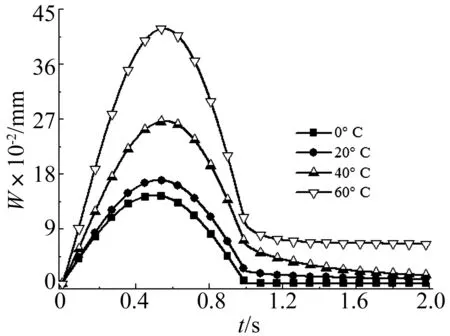
图3 不同温度时，载荷作用面中心O处的下沉量变化Fig.3 Launching site settlement of circle center O at different temperature

黏弹性材料的总应变由弹性应变以及蠕变应变(非弹性应变)组成，弹性应变在载荷卸载后可以完全恢复，蠕变应变只能部分恢复，造成场坪永久变形。对比面层温度为20℃、40℃、60℃时场坪的响应情况，由于温度越高，蠕变应变在总应变中的比例越大，因此载荷卸载后，弹性恢复过程越缓慢，场坪的残余弯沉越大。

图4～图7分别给出了面层温度为0℃、20℃、40℃、60℃时不同观测点处场坪表面下沉量的变换情况。从中可知：① 距载荷作用面越远的观测点，垂向位移越小，载荷卸载后的残余变形亦越小。② 比较不同温度下各个观测点下沉量最大差值可以看出，温度越高，场坪表面的局部弯沉现象越明显。

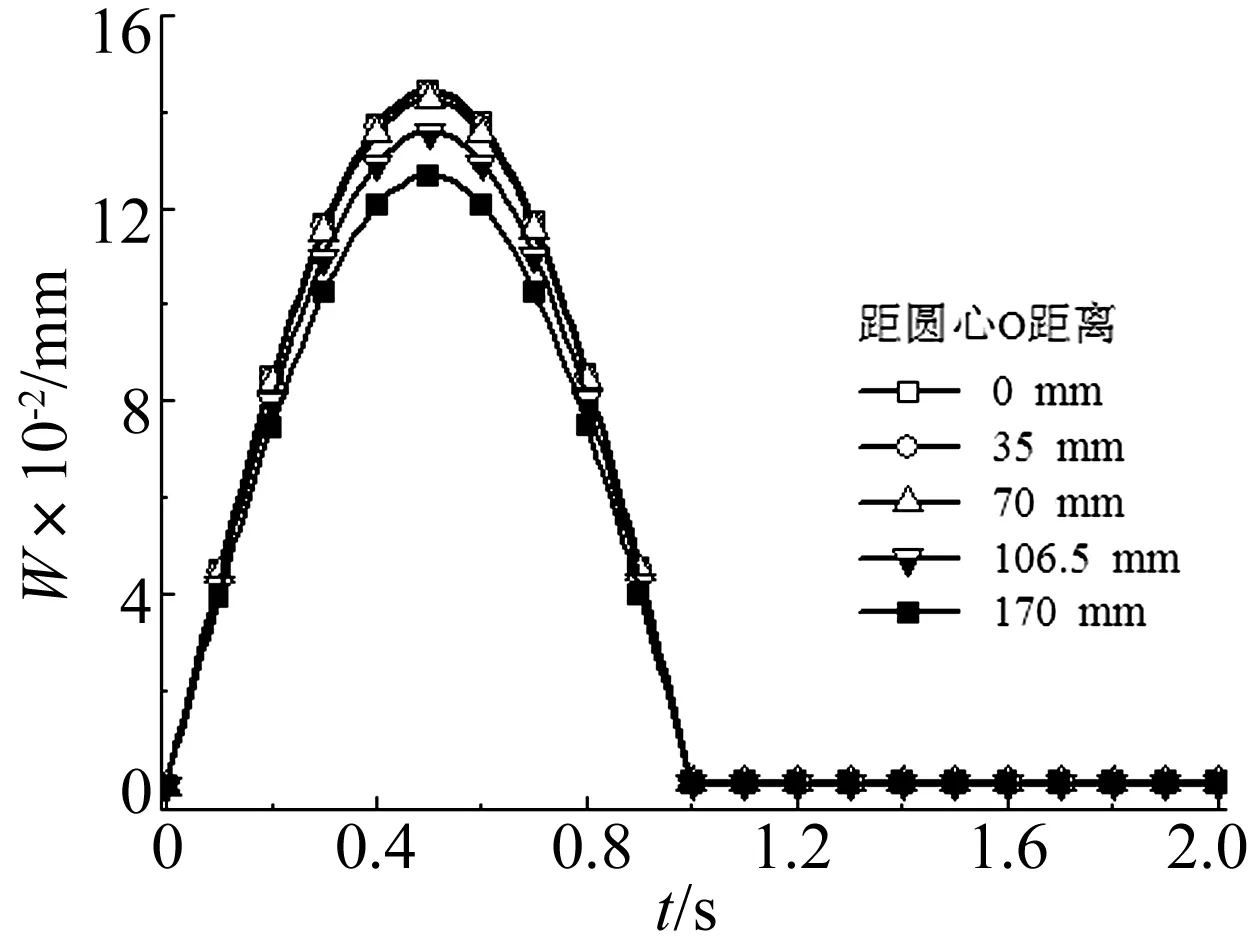
图4 面层温度为0℃度时，场坪表面不同观测点的下沉量变化Fig.4 Launching site settlement of different points at surface course temperature 0℃

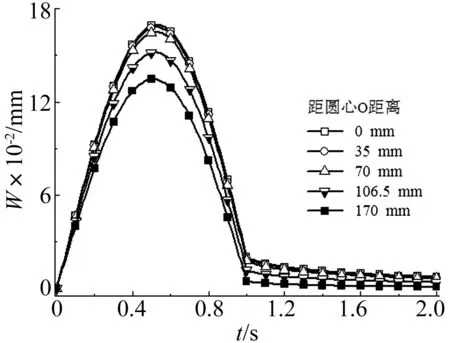
图5 面层温度为20℃度时，路表不同观测点的下沉量变化Fig.5 Launching site settlement of different points at surface course temperature 20℃

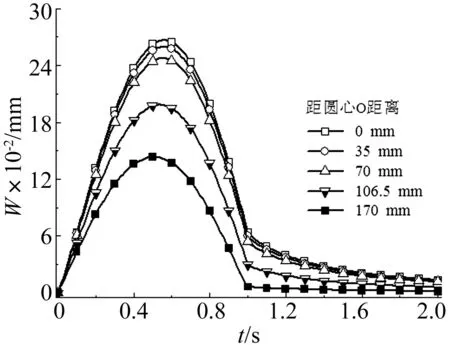
图6 面层温度为40℃度时，场坪表面不同观测点的下沉量变化Fig.6 Launching site settlement of different points at surface course temperature 40℃

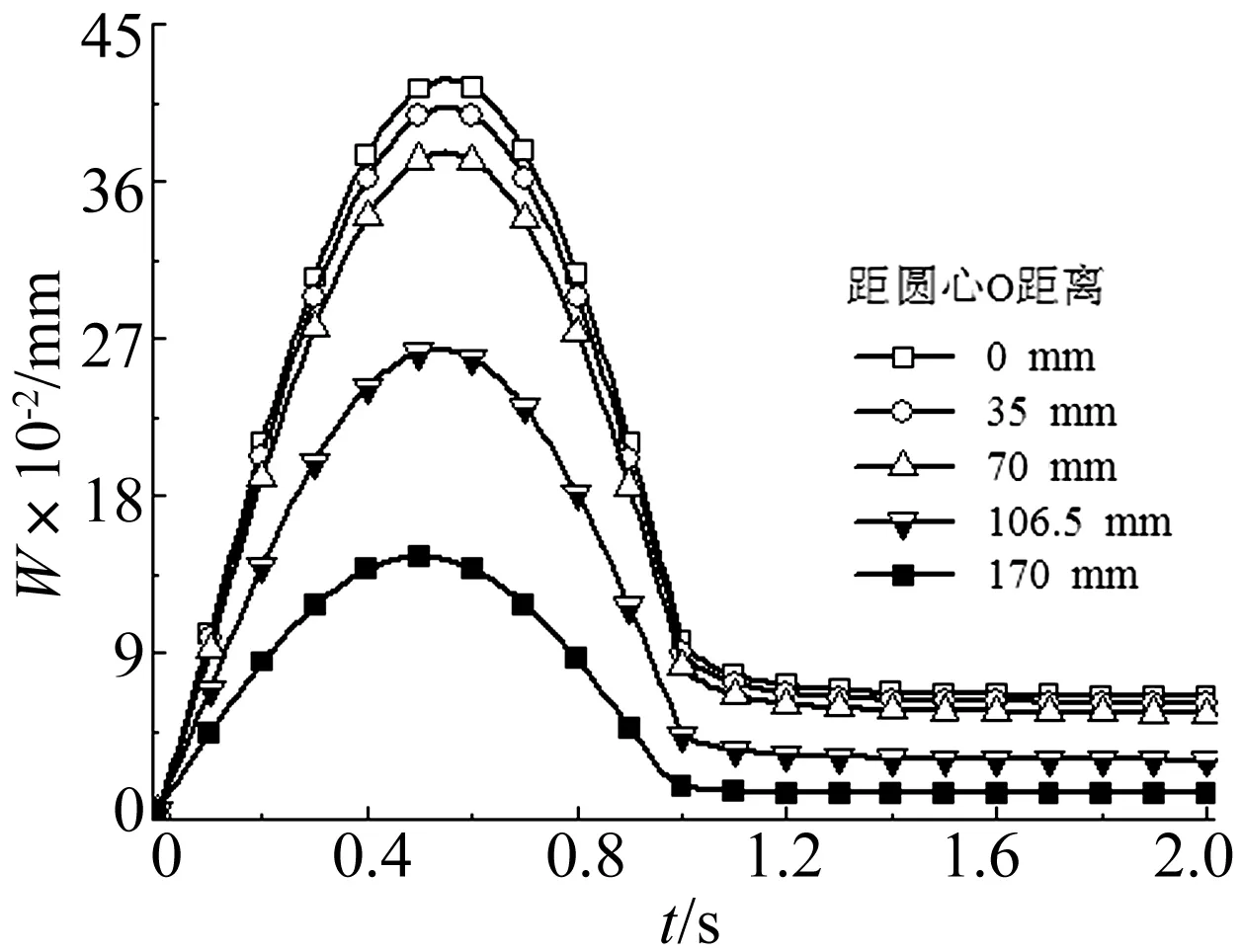
图7 面层温度为60℃度时，场坪表面不同观测点的下沉量变化Fig.7 Launching site settlement of different points at surface course temperature 60℃

5 结 论

将“时温等效”原理与广义Maxwell黏弹性模型结合以反映温度对材料力学性能的影响，根据直角坐标系下黏弹性问题的基本方程，通过Laplace变换和二维Fourier变换，建立了多层黏弹性体系的传递关系，研究了考虑温度效应的圆形均布动载荷下场坪的动力响应，通过分析可得出以下结论：

(1) 温度越高，场坪表面的下沉量越大，局部弯沉现象越明显，载荷卸载后残余弯沉也越大。

(2) 温度较低时，沥青混凝土的黏弹性特性可以忽略，可视场坪面层为线弹性体。

[1] 任瑞波, 谭忆秋, 张肖宁. FWD动载荷作用下沥青路面层状体黏弹性解与弹性解分析[J]. 哈尔滨建筑大学学报, 2001, 34(5): 116-120.

REN Ruibo, TAN Yiqiu, ZHANG Xiaoning. So1ution of multilayered viscoeIastic and elastic bodies of asphalt pavement under action of FWD dynamical load[J]. Journal of Harbin University of C. E. & Architecture, 2001, 34(5): 116-120.

[2] 任瑞波, 谭忆秋, 张肖宁. FWD动载荷作用下沥青路面层状体路表弯沉的求解[J]. 中国公路学报,2001,14(2): 9-17.

REN Ruibo, TAN Yiqiu, ZHANG Xiaoning. Solution for solving asphalt pavement multilayered viscoelastic body surface deflection in the FWD dynamic case[J]. China Journal of Highway and Transport, 2001, 14(2): 9-17.

[3] 王有凯, 牛婷婷. 直角坐标系下层状地基力学计算中的传递矩阵技术[J]. 工程力学, 2007, 24(增刊1): 83-86.

WANG Youkai, NIU Tingting. The method of transferring matrix for multi-layered half space elastic problems in rectangular coordinate system[J]. Engineering Mechanics, 2007, 24(Sup1): 83-86.

[4] 艾智勇, 吴超. 三维直角坐标系下分层地基的传递矩阵解[J].重庆建筑大学学报, 2008, 30(2): 43-46.

AI Zhiyong, WU Chao. Transfer matrix solutions for multi-layered soils in rectangular coordinate system[J]. Journal of Chongqing Jianzhu University, 2008, 30(2): 43-46.

[5] 汤连生, 徐通, 林沛元, 等. 交通荷载下层状道路系统动应力特征分析[J]. 岩石力学与工程学报, 2009, 28(增刊2): 3876-3884.

TANG Liansheng, XU Tong, LIN Peiyuan, et al. Study on dynamic stress characters of layered road system under traffic loading [J]. Chinese Journnl of Rock Mechnnics and Engineering, 2009, 28(Sup2): 3876-3884.

[6] 董忠红, 吕彭民. 移动荷载下黏弹性层状沥青路面动力响应模型[J]. 工程力学, 2011, 28(12): 153-159.

DONG Zhonghong, LÜ Pengmin. A model to study the dynamic response of viscoelastic layered system under moving load[J]. Engineering Mechanics, 2011, 28(12): 153-159.

[7] 李皓玉, 杨绍普, 刘进, 等. 移动分布荷载下层状黏弹性体系的动力响应分析[J]. 工程力学,2015,32(1):120-127.

LI Haoyu, YANG Shaopu, LIU Jin, et al. Dynamic response in multilayered viscoelastic medium generated by moving distributed loads[J]. Engineering Mechanics, 2015, 32(1): 120-127.

[8] 艾智勇, 王陆君, 曾凯. 稳定温度场下层状路面体系的解析层元解[J]. 同济大学学报(自然科学版),2014,42(11):1665-1669.

AI Zhiyong, WANG Lujun, ZENG Kai. Analytical layer-element solution for layered pavement in stable temperature field[J]Journal of Tongji University (natural science), 2014, 42(11): 1665-1669.

[9] 刘小云, 史春娟. 车辆荷载下沥青路面动力响应随机特性及可靠性分析[J]. 中国公路学报, 2012, 25(6): 49-55.

LIU Xiaoyun, SHI Chunjuan. Random characteristics and reliability analysis of asphalt pavement under vehicle random load[J]China Journal of Highway and Transport,2012,25(6): 49-55.

[10] 史春娟, 吕彭民. 基于非线性模型的沥青路面动力响应研究[J]. 工程力学, 2013, 30(2): 326-347.

SHI Chunjuan, LÜ Pengmin. Study on the dynamic response of asphalt pavement based on the nonlinear viscoelastic model[J]. Engineering Mechanics, 2013, 30(2): 326-347.

[11] 卢正, 姚海林, 胡智. 基于车辆-道路结构耦合振动的不平整路面动力响应分析[J]. 岩土工程学报, 2013, 35(增刊1): 232-238.

LU Zheng, YAO Hailin, HU Zhi. Dynamic response analysis of rough pavement under vehicle-road system coupled vibration[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Sup1): 232-238.[12] 张震东, 马大为, 任杰, 等. 冷发射装备对地载荷作用下预设场坪的动力响应[J]. 兵工学报, 2015, 36(2):279-286.

ZHANG Zhendong, MA Dawei, REN Jie, et al. Dynamic response of cold launching equipment to prepared launching site subjected to loading[J]. Acta ArmamentarII,2015,36(2):279-286.

[13] 赵延庆, 钟阳. 沥青路面动态黏弹性相应分析[J]. 振动与冲击, 2009, 28(9): 159-162.

ZHAO Yanqing, ZHONG Yang. Dynamic response analysis of viscoelastic asphalt mixtures pavement[J]. Journal of Vibration and Shock, 2009, 28(9): 159-162.

[14] 张丽娟, 陈页开. 重复荷载下沥青混合料变形的黏弹性有限元分析[J]. 华南理工大学学报(自然科学版), 2009, 37(11): 12-16.

ZHANG Lijuan, CHEN Yekai. Viscoelastic finite element analysis of deformation of asphalt mixtures under repeated load[J]. Journal of South China University of Technology (Natural Science Edition) , 2009, 37(11): 12-16.

[15] 周晓和, 马大为, 胡建国, 等. 某导弹无依托发射场坪动态响应研究[J]. 兵工学报, 2014, 35(10): 1595-1603.

ZHOU Xiaohe, MA Dawei, HU Jianguo, et al. Research on dynamic response of Launching Site for missile unsupported random launch[J]. Acta ArmamentarII, 2014，35(10): 1595-1603.

[16] 钱国平, 郭忠印, 郑健龙, 等. 环境条件下沥青路面热黏弹性温度应力计算[J]. 同济大学学报, 2003, 31(2): 150-155.

QIAN Guoping, GUO Zhongyin, ZHENG Jianlong, et al. Calculation for thermal stress of asphalt pavement under environmental conditions based on thermalviscoelasticity theory[J]. Journal of Tongji University, 2003, 31(2): 150-155.

[17] DURBIN F. Numerical inversion of laplace transforms．an efficient improvement to dubner and abate’s method[J]．The Computer Journal, 1973,17(4): 371-376.

Dynamic response of an asphalt launching site under circular distributed load considering temperature effect

ZHANG Zhendong1, MA Dawei1, YANG Yun2, HE Qiang1

(1. College of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;2. College of Transportation, Huanghe College of Science and Technology, Zhengzhou 450000, China)

By transforming viscoelastic materials’ integral type constitutive equation with Laplace Transformation, the viscoelastic operator described with Maxwell model was deduced. Then time-temperature equivalent principle was introduced to reflect the influence of temperature on mechanical property of asphalt concrete. By means of Laplace transformation and Fourier transformation for dynamic equilibrium equations, geometric equations and physical equations of visco-elastic problems in a rectangular coordinate system, the transfer matrix of axisymmetrical problems in a multi-layered viscoelastic half space was derived. Based on the transferring relation and known boundary conditions, the solution to surface vertical displacements of an asphalt launching site was derived and the computing program was complied by using MATLAB software. Taking a three-layer launching site as an example, its dynamic response under circular distributed load was analyzed. Results indicated that the settlement and residual deflection increase gradually with increase in temperature; the higher the temperature, the more obvious the local deflection phenomenon.

temperature effect; viscoelasticity; asphalt launching site; transfer matrix; dynamic response

装备预先研究项目(51328020106)

2015-07-10 修改稿收到日期：2015-11-02

张震东 男，博士生，1988年生

马大为 男，教授,博士生导师，1953年生

TJ768.1

A

10.13465/j.cnki.jvs.2016.19.015