复合材料波纹板在剪切载荷下的屈曲特性分析与可靠性优化

郑宇宁 ， 邱志平 ， 苑凯华

(1.北京航空航天大学 航空科学与工程学院，北京 100191； 2.北京机电工程研究所，北京 100074)



复合材料波纹板在剪切载荷下的屈曲特性分析与可靠性优化

郑宇宁1， 邱志平1， 苑凯华2

(1.北京航空航天大学 航空科学与工程学院，北京 100191； 2.北京机电工程研究所，北京 100074)

飞机机翼的墙腹板广泛采用复合材料波纹板结构，该结构在剪切载荷作用下的屈曲可靠性是其设计中必须考虑的因素。基于波纹板等效拉伸和弯曲刚度模型，采用Ritz法和最小势能原理，推导了复合材料波纹板临界剪切屈曲载荷的计算方法；充分考虑复合材料属性及外载荷中存在的不确定性，采用区间向量实现不确定参数的定量化；借助参数顶点法确定屈曲载荷因子的上下界,提出了剪切载荷作用下屈曲可靠性的区间分析方法；利用区间可能度指标刻画剪切屈曲可靠度，建立了含不确定参数的复合材料波纹板区间可靠性优化模型。数值算例表明，该方法与有限元方法(FEM)相吻合，优化结果验证了所建立的区间可靠性优化模型及算法的有效性。

复合材料；波纹板；屈曲；不确定性；区间分析；可靠性优化

复合材料波纹板由于具有良好的承载能力和稳定性，在现代飞行器结构设计中得到了广泛应用，如美国X-15高超声速飞行器采用了波纹板结构蒙皮，F-22隐形战斗机将正弦波纹腹板梁应用在机翼和尾翼结构中，而NASA的兰利研究中心早在1963年就展开了对波纹板结构弯曲刚度和扭转刚度的研究[1]，并将研究成果应用于飞行器结构的概念设计阶段。

复合材料波纹板在飞行器结构中的大量应用，促使国内外学者探索波纹板结构的等效简化刚度模型，以提高计算效率。BRIASSOULIS[2]对各向同性正弦型波纹板的等效弯曲刚度进行了预测；SAMANTA等[3]将梯形波纹板等效为正交各向异性平板，推导并给出了其等效拉伸和弯曲刚度；YOKOZEKI等[4]计算了U形波纹板的拉伸和弯曲模量，并与实验结果进行了对比；XIA等[5]基于应变能守恒原理推导了复合材料波纹板等效刚度的表达式，并利用有限元模型验证了该方法的合理性。

针对波纹板屈曲稳定性的研究在国内外也取得了一定进展。LIEW等[6]基于一阶剪切变形理论，将波纹板近似成等刚度的正交各向异性板，研究了加筋和无加筋波纹板的弹性屈曲问题；WENNBERG等[7]研究了原始波纹板模型与等效正交各向异性平板模型在轴向载荷作用下的稳定性问题，其结果显示利用等效简化刚度模型计算波纹板屈曲载荷具有较高精度；SHAW等[8]分析了应用于智能飞行器柔性蒙皮结构中的复合材料波纹板屈曲模态；吴存利等[9]采用工程算法和有限元方法计算了复合材料波纹板的临界屈曲载荷，并利用修正因子对有限元计算值和工程计算值进行了修正。

然而，以上针对复合材料波纹板屈曲问题的研究大多是从工程算法角度给出临界屈曲载荷计算值，并且都是在确定性范围内进行的。在实际工程中，复合材料受到加工工艺、制造工艺、试验环境[10]等诸多随机因素的影响，其材料属性包括(弹性模量、剪切模量、泊松比)及外载荷具有一定的不确定性[11]。针对复合材料属性及外载荷中客观存在的不确定因素，HAN等[12]基于非线性区间规划方法开展了考虑材料属性不确定性的复合材料层合板结构优化设计；许孟辉等[13]考虑了材料参数及外载荷中的不确定因素，基于模糊方法进行了复合材料点阵夹芯结构平压性能不确定分析与优化。但是，关于不确定环境下复合材料波纹板剪切屈曲性能的分析与优化研究还未见有报道。

鉴于此，本文首先推导了复合材料波纹板临界剪切屈曲载荷的计算方法，与有限元方法进行了验证比较；在此基础上，考虑复合材料参数及外载荷中不确定性对波纹板剪切屈曲性能的影响，建立了含不确定参数复合材料波纹板区间可靠性优化模型及算法。最后，通过数值算例表明本文方法可以实现波纹板结构轻质、可靠的设计目标。

1 复合材料波纹板的等效力学模型

复合材料梯形波纹板的结构形式如图1所示，其中波纹板沿波纹方向的长度为a，展向长度为b。图2所示为在笛卡尔坐标系和曲线坐标系下定义的梯形波纹板截面外形。梯形波纹板由正交各向异性层合板构成，其中y和s为材料主方向。为了定量描述两种坐标系之间的联系，在曲线坐标系中引入位置向量r=r(s,y) ，可表示为如下形式：

r(s,y)=x(s)i+yj+z(s)k

(1)

式中：i,j,k为x,y,z方向的单位向量。在曲线坐标系中的单位切向量et与法向量en定义为：

(2)

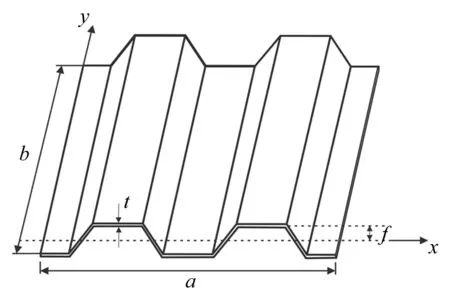
图1 波纹板简图Fig.1 Sketch of corrugated plate

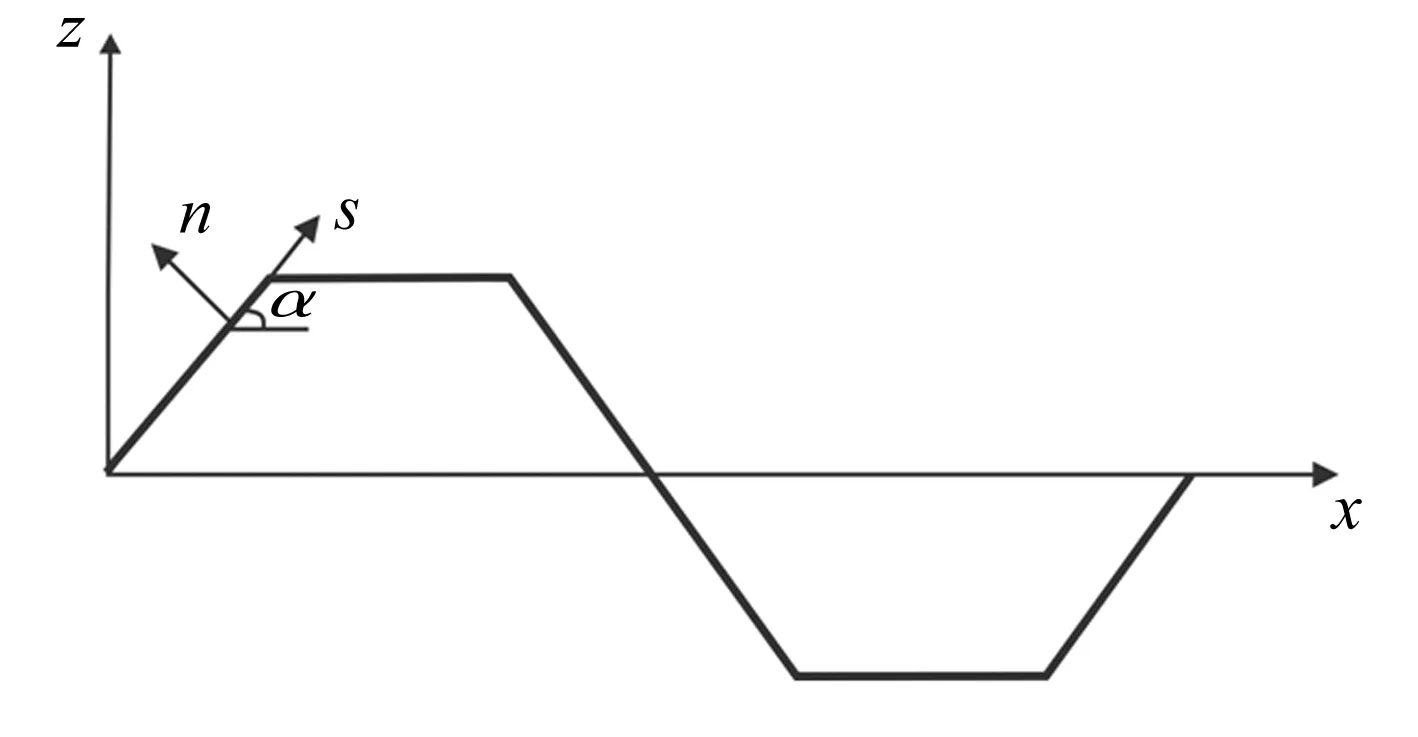
图2 坐标系定义Fig.2 Definition of the coordinate systems

当波纹板整体尺寸与板厚度的比值足够大且波纹周期及截面高度与波纹板尺寸相比较小时，基于复合材料的均匀化理论[5]，可以将复合材料波纹板等效为正交各向异性平板，如图3所示，其本构方程为：

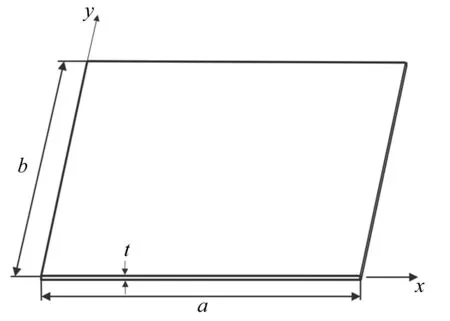
图3 等效正交各向异性平板Fig.3 Equivalent orthotropic plate

(3)

(4)

在曲线坐标系下，波纹板的应变能U1可以表示为：

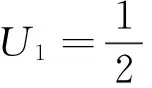
(5)

式中：N波纹板结构的内力和内力矩，C为柔度矩阵。同时，可由式(3)得出等效正交各向异性平板的应变能U2为：

(6)

根据应变能守恒原理，不同坐标系下计算的应变能U1和U2满足U1=U2。对于如图4所示的波纹板截面构型，其中f为梯形波纹板的半波高，c和l分别为梯形波纹板半波的弦长和周长，θ为梯形截面的倾角，t为波纹板的厚度，表1给出了基于复合材料均匀化理论及应变能守恒原理推导的梯形波纹板等效拉伸和弯曲刚度的表达式。

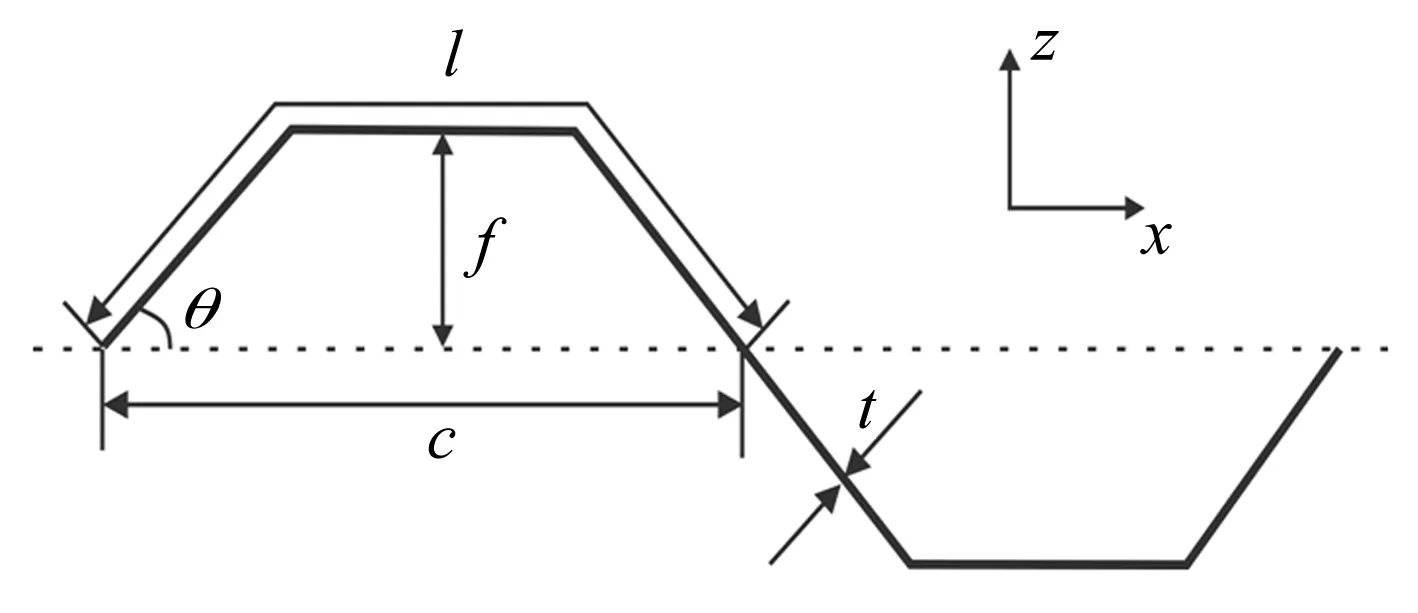
图4 梯形波纹板截面构型Fig.4 Cross section configuration of trapezoidal corrugated plate

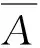
(7)

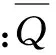
表1 复合材料波纹板的等效刚度特性

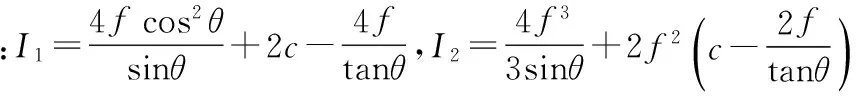
2 复合材料波纹板的临界剪切屈曲载荷

在工程实际中，应用于机翼墙腹板中的复合材料波纹板主要承担剪力，因此，在设计中主要分析波纹板在剪切载荷作用下的屈曲可靠性。受均布剪切载荷作用下的复合材料梯形波纹板如图5所示。

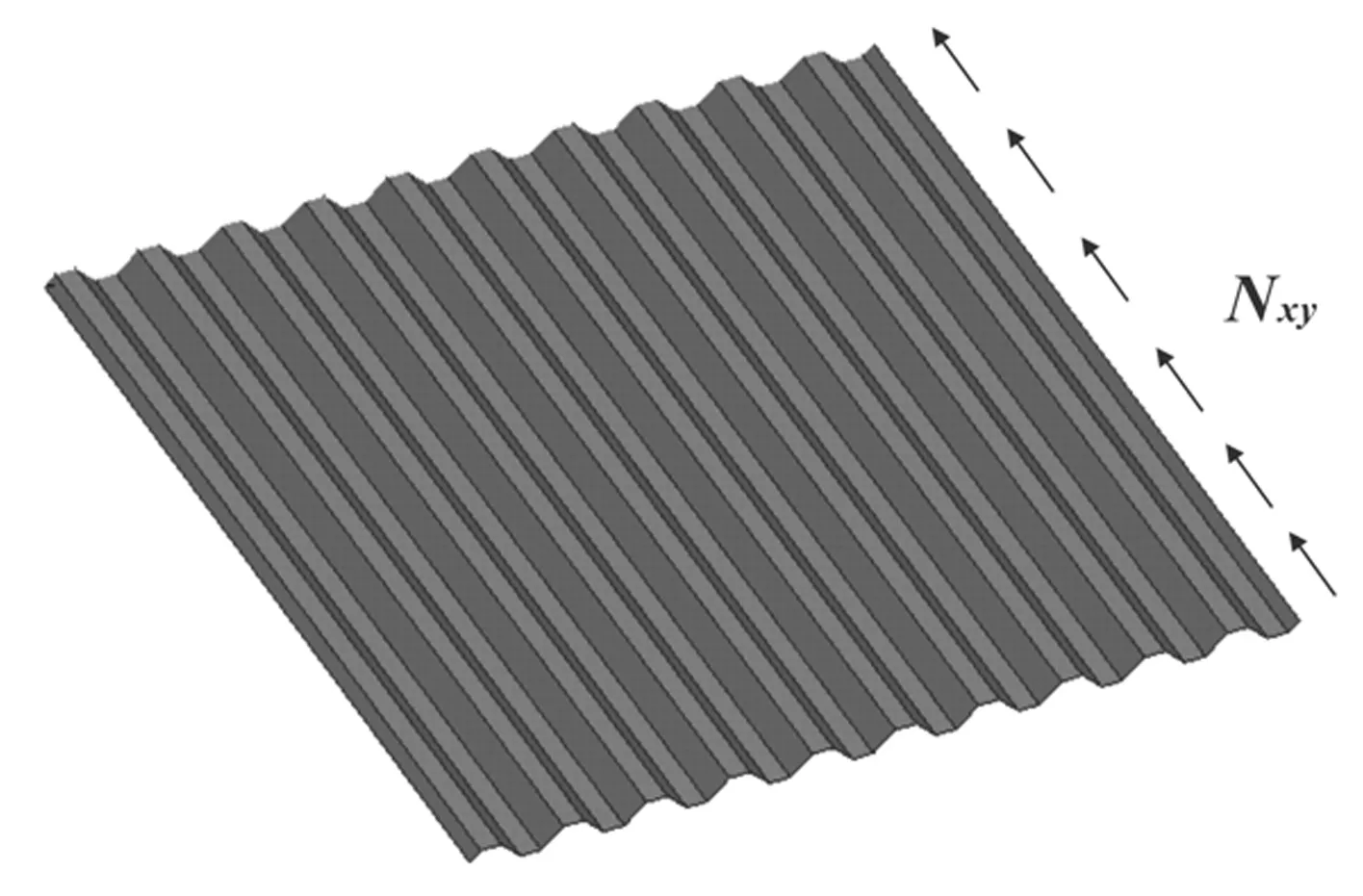
图5 剪切屈曲分析模型Fig.5 Shear buckling analysis model

其中，复合材料波纹板由正交各向异性层合板构成，并假定层合板的铺层是对称的，即耦合刚度矩阵B=0；弯曲刚度D近似为正交各向异性，即假设D16=D26=0。当波纹板的波形较密时，在剪切载荷作用下将主要发生整体屈曲[14]。计算整体屈曲载荷时，可将复合材料波纹板等效为正交各向异性平板。利用等效方法，并根据以上条件得出Von Karman正交各向异性板大挠度方程[15]为：

(8)

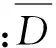
(9)

假设板的边界条件为四边简支，即：

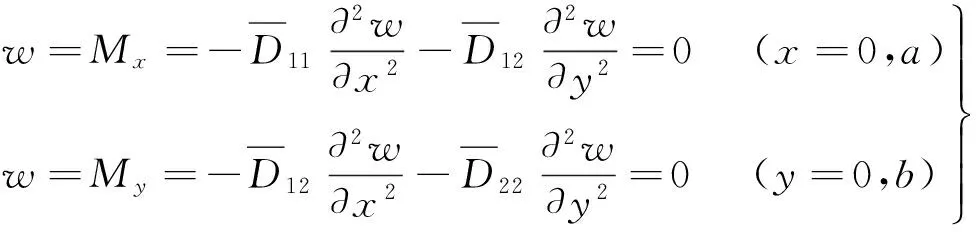
利用Ritz法，取满足式(10)中四边简支边界条件的双三角级数作为板的挠度：

(11)

式中：wmn为m和n对应的系数。

正交各向异性平板弯曲应变能具有如下形式：

(12)

板弯曲时剪切载荷做的功为：

(13)

将式(11)分别代入式(12)和式(13)，得出

(14)

W=

(15)

式中：m,n,p,q满足条件

m±p=奇数 ，n±q=奇数

(16)

板的总势能表达式为：

Π=U-W

(17)

利用极小势能原理，当总势能取最小值时，对每一个系数wmn有以下关系：

(18)

将式(14)～式(17)代入式(18)，并记此时的载荷为临界屈曲载荷(Nxy)cr，得到以下关于wmn的线性方程组：

(19)

式中:

(20)

(21)

为便于表示波纹板在均布剪切载荷作用下的屈曲可靠性，这里引入屈曲载荷因子λ，其定义为：

(22)

式中：Nxy表示实际作用在波纹板上剪切载荷。将式(22)代入式(19)，并以矩阵形式表达为：

(K-λG){w}={0}

(23)

式中：K和G分别为波纹板的等效刚度系数矩阵和初应力刚度系数矩阵。可以看出，式(23)是关于系数w的广义特征值方程。当w11=w12=…=wmn=0时，即板的挠度为零，此时板还未发生屈曲；当且仅当w11,w12,…,wmn不全为零(对应非零挠度)时，才有可能求出屈曲载荷因子。而广义特征值方程(23)存在非零解的充要条件是其系数矩阵行列式等于零[16]，即：

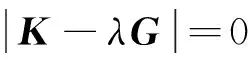
(25)

求解该行列式，可以得到关于λ的多项式方程：

F(λ)=0

(26)

满足上式所得的λ中的最小值即为波纹板的屈曲载荷因子。对于式(25)中的方程，采用具有全局收敛性的Laguerre迭代法[17]进行求解，其迭代公式如下：

(k=0,1,2,…)

(26)

式中:

H(λ)=

(s-1)[(s-1)(F′(λ))2-sF(λ)F″(λ)]

(27)

这里s是多项式F(λ)的次数。

3 区间可靠性优化方法

3.1 屈曲载荷因子的区间分析方法

对于复合材料波纹板结构，由于其材料属性及外部载荷环境中存在的不确定性种类繁多且复杂，在试验数据不足的条件下获取不确定参数的概率特征非常困难。与概率方法相比，区间方法仅需明确不确定参数的分布界限，通过较少信息获得其变动范围是容易实现的。将材料属性及外载荷中的不确定参数向量记为φ，即：

φ=(φ1,φ2,…,φr)T

(28)

式中：r为不确定参数向量的个数。φ可用如下的区间形式表示：

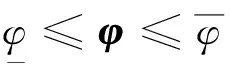
(29)

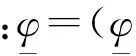
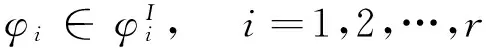
(30)

式中:

(31)

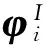
K=K(φ), G=G(φ)

(32)

在约束条件(式(30))下，最小特征值即屈曲载荷因子λ的集合可以写为：

Γ={λ:λ∈R,K(φ){C}=

λG(φ){C}, φ∈φI}

(33)

式中:：

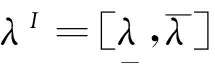
(34)

式中：

(35)

将区间参数向量φ的边界向量定义为：

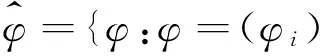
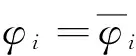
(36)

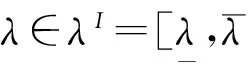
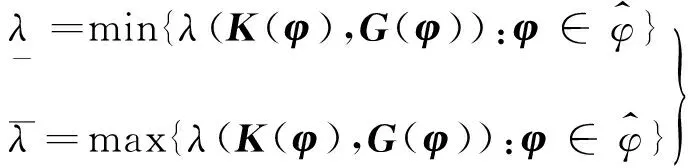
(37)

3.2 区间可靠性优化模型

传统的确定性优化设计方法是在材料属性及外载荷等系统参数确定的情况下寻求设计变量的最优解，对系统中可能存在的不确定因素一般通过引入安全因子来表达。区间可靠性优化方法在设计阶段就充分考虑不确定因素的影响，采用区间参数对不确定信息进行定量化表征，建立约束条件的区间数学模型，通过主动控制措施保证结构的稳定性，其优化模型为：

(38)

式中：f(X)是设计目标的性能函数；X为设计变量向量；φ为不确定参数向量；gi(X,φ)为约束条件；n为约束条件的个数。在计及不确定因素波动变化条件下，为了实现结构的安全可靠性，应使优化问题中的约束条件能够表征不确定性的波动影响，即将其写为：

Poss(gi(X,φ)≤0)≥ηi， (i=1,2,…,n)

(39)

式中：Poss为函数概率算子；ηi∈[0,1]为区间可能度指标，反映波纹板在剪切载荷下的屈曲可靠度。

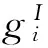
Poss(AI>BI)=

(40)

(41)

式中:

(42)

基于以上数学模型约束条件进行可靠性处理，可以得到含区间参数的可靠性优化设计模型。利用参数顶点求解定理，可以近似求取含区间参数的约束条件响应范围，从而避免了对内层不确定区间参数的优化，将原本的两层嵌套优化问题转换为单层优化，极大地改善了优化效率。同时，本文采用基于模拟退火(SA)算法的最佳值搜索算法，与传统优化算法相比，SA算法可以在控制温度的作用下对参数值进行调整，还能以较小的概率接受恶劣解，在搜索过程中灵活性强，不易于陷入局部优化解。

4 数值算例

4.1 剪切屈曲载荷的计算方法验证

采用如图6所示具有10个周期的梯形波纹板结构。其中，a=b=1 016 mm，c=50.8 mm，f=12.7 mm，t=2 mm，梯形截面倾角θ=45°。复合材料波纹板由AS4/3501-6碳/环氧复合材料构成，材料属性如表2所示，铺层顺序为[0°/90°]s，各单层板的厚度d=0.5 mm。

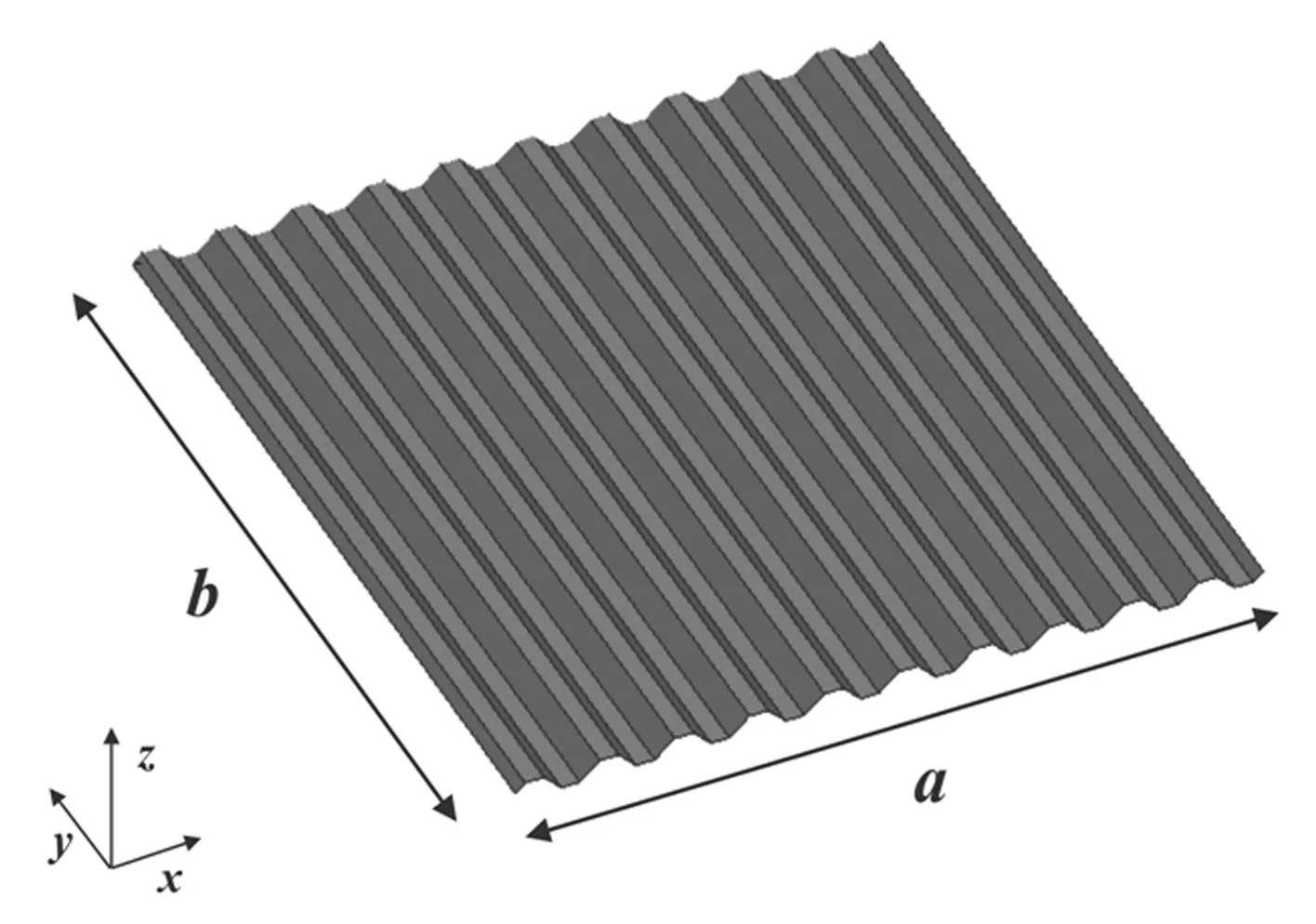
图6 梯形波纹板结构图Fig.6 Trapezoidal corrugated plate structure

属性E1/GPaE2/GPav12G12/GPaρ/(kg·m-3)值14810.50.35.61580

首先对复合材料波纹板的等效刚度进行验证。图7给出了x-z和y-z平面内原始梯形波纹板与具有等效刚度的正交异性板在均布面压作用下的法向位移曲线。从图中可以看出，利用等效能量法计算得到的等效刚度与原始波纹板相比略微偏小，其原因是与等效正交各向异性板相比，原始梯形波纹板在沿波纹方向受到了多余约束，但从总体上看等效板的刚度能够较精确地反映原始波纹板的刚度特性。

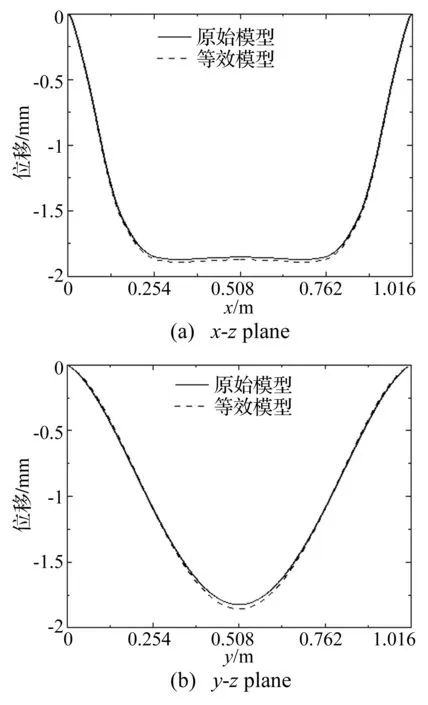
图7 x-z和y-z平面内梯形波纹板的位移Fig.7 The displacement in the x-z and y-z planes for trapezoidal corrugated plate structure

在分析等效刚度的基础上，采用壳单元建立如图8所示的梯形波纹板有限元模型，单元总数为8 000，边界条件如表3所示，同时在BC边上施加Nxy=150 kN/m的剪切载荷。利用MSC.Nastran的屈曲分析模块计算复合材料梯形波纹板在剪切载荷作用下的屈曲载荷因子，以验证本文计算方法的合理性。

利用波纹板有限元模型和本文建立的等效方法计算得到的屈曲载荷因子随外形参数的变化趋势如图9和图10所示。从图中可以看出，当波纹板的半波高f较小时，在给定参数变化范围内，本文给出的计算结果与利用MSC.Nastran进行屈曲分析得到的计算结果之间的误差很小，与有限元分析结果吻合较好。随着波纹板半波高f及截面倾角θ的增大，两种方法得到的计算结果之间的误差有小幅增长，但与有限元分析结果相比，本文计算结果相对保守。因此，在进行波纹板屈曲稳定性优化设计时，可将其作为计算屈曲载荷因子的近似模型，在保证结构安全可靠的条件下提高优化效率。

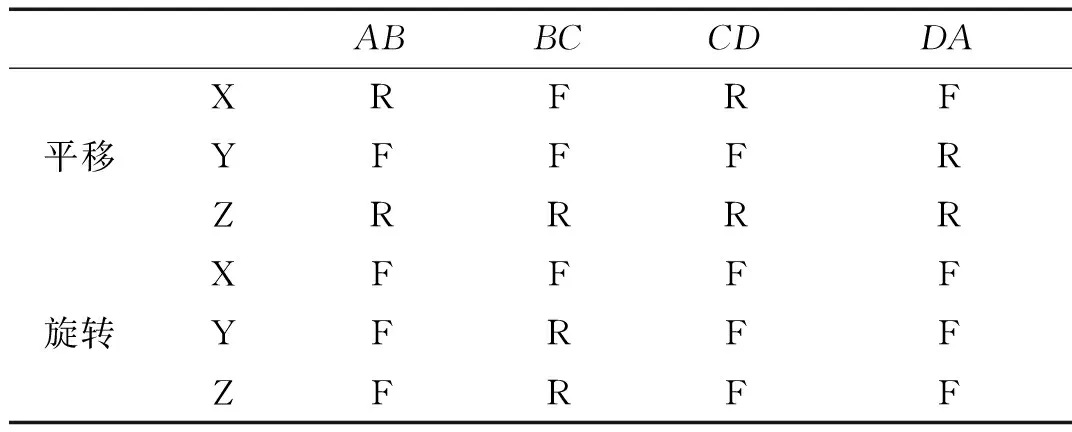
表3 有限元模型的边界条件

注:R表示有约束，F表示无约束。

4.2 优化算例

以复合材料波纹板梯形截面的半波高f和倾角θ作为外形设计变量，初始设计中，取半波高f=12.7 mm，截面倾角θ=45°。同时，选取波纹板结构总质量M(X)最小化作为目标函数，屈曲载荷因子λ不小于1作为约束条件，优化模型如下所示：

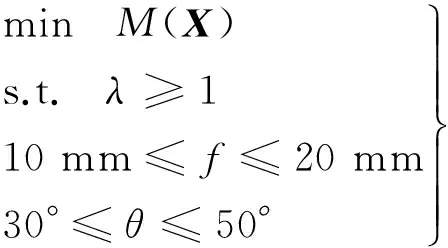
(43)

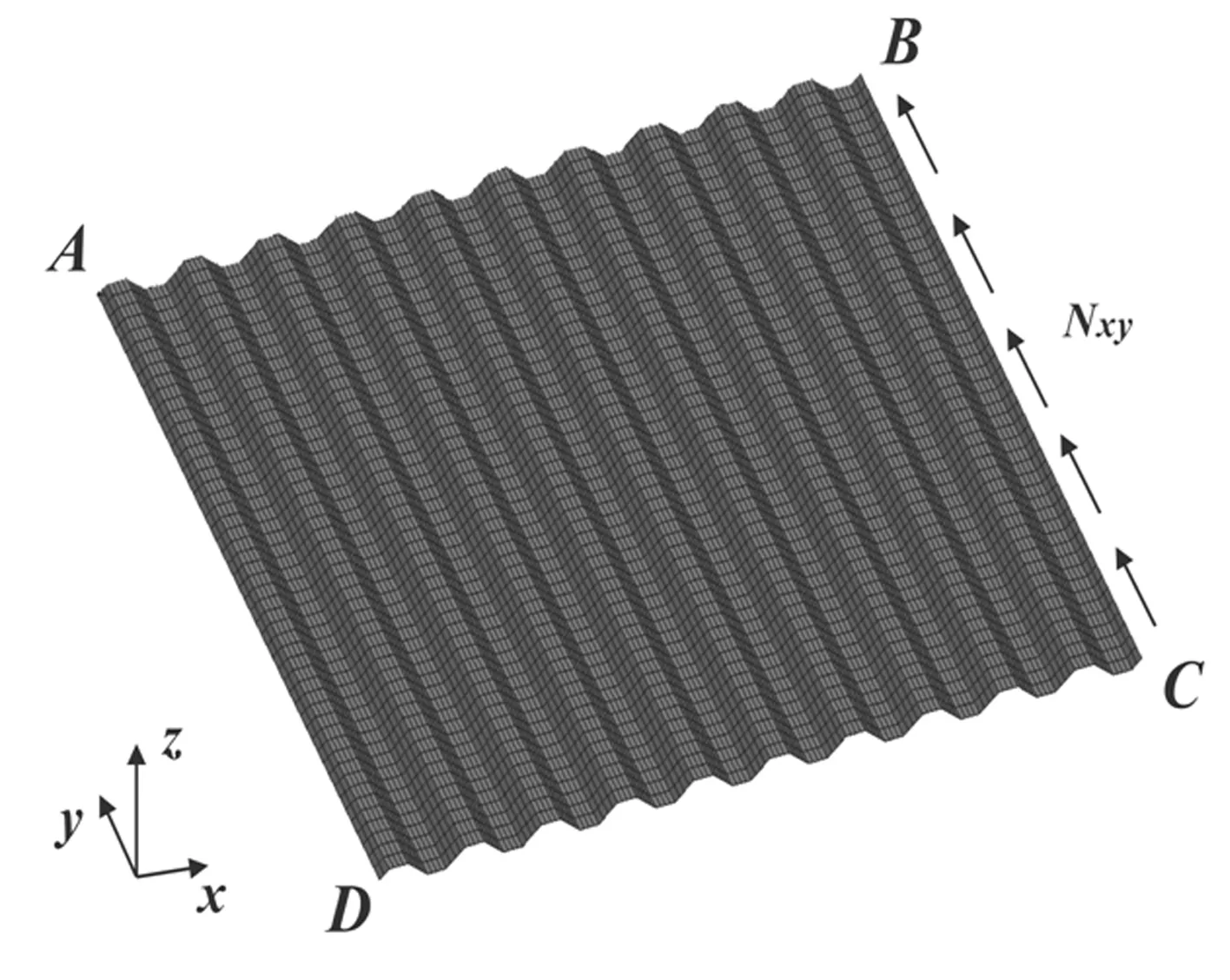
图8 有限元模型Fig.8 Finite element model

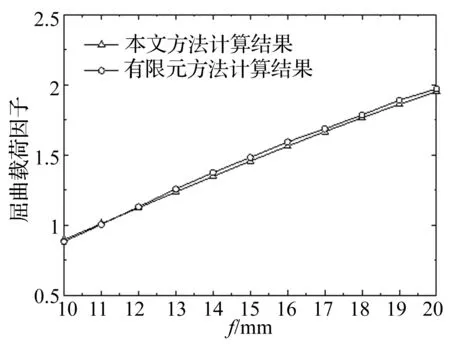
图9 屈曲载荷因子随f的变化Fig.9 Variation of the buckling load factor with f

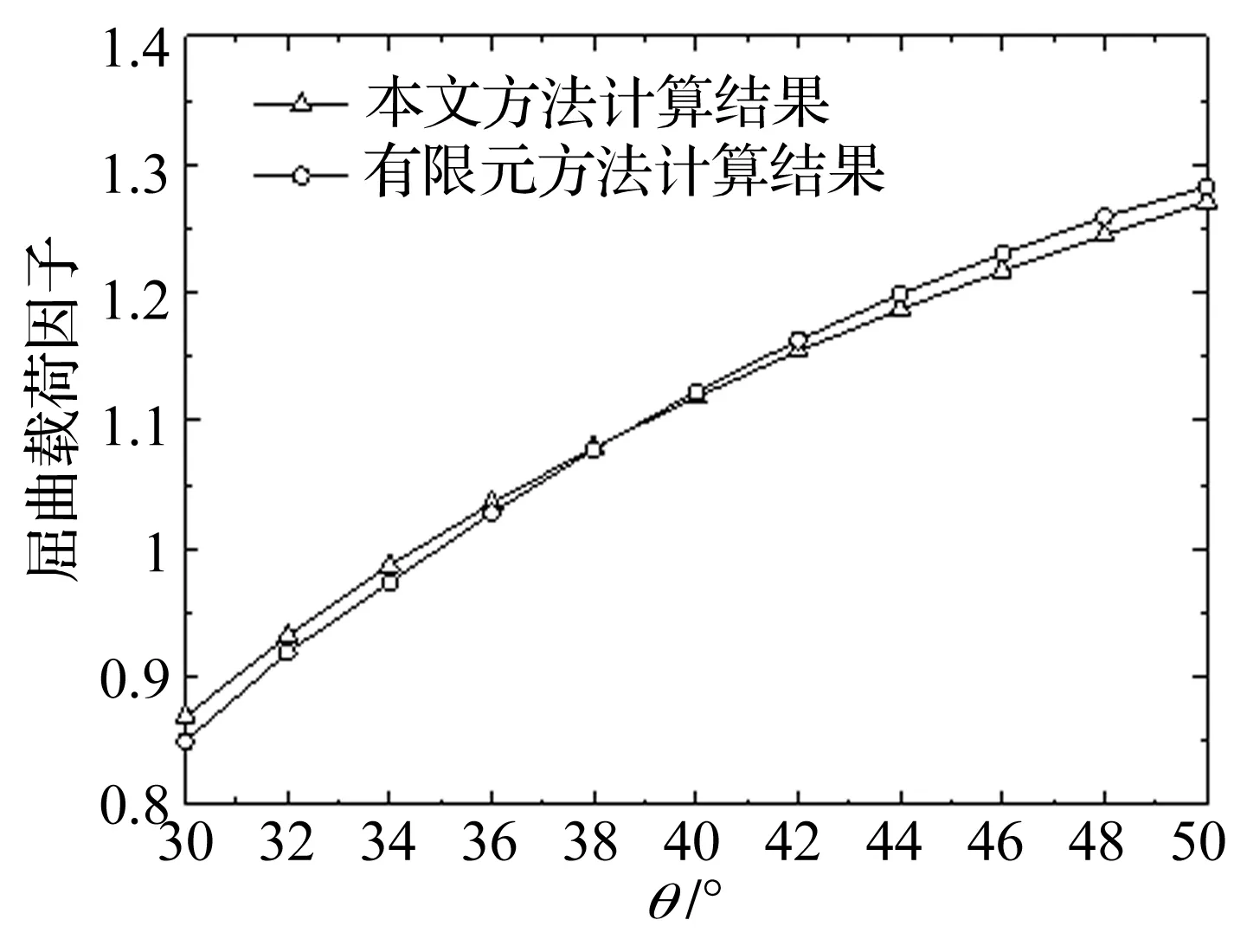
图10 屈曲载荷因子随θ的变化Fig.10 Variation of the buckling load factor with θ

实际工程问题中，由于复合材料的初始缺陷及测量误差，其材料属性参数E1,E2,v12,G12及外载荷参数Nxy均为不确定参数，它们的变化区间为E1∈[140,156] GPa,E2∈[10,11]GPa,G12∈[5.3,5.9] GPa,v12∈[0.27,0.33],Nxy∈[1.49E+005,1.51E+005] N/m。利用区间分析方法，可以建立如下的区间可靠性优化模型：

(44)

采用SA算法，结合本文给出的屈曲载荷的工程计算方法，利用区间可靠性优化模型和确定性优化模型对复合材料波纹板截面外形进行优化设计。在可行域范围内，外形设计参数及波纹板总质量的优化搜索迭代过程如图11～图13所示。

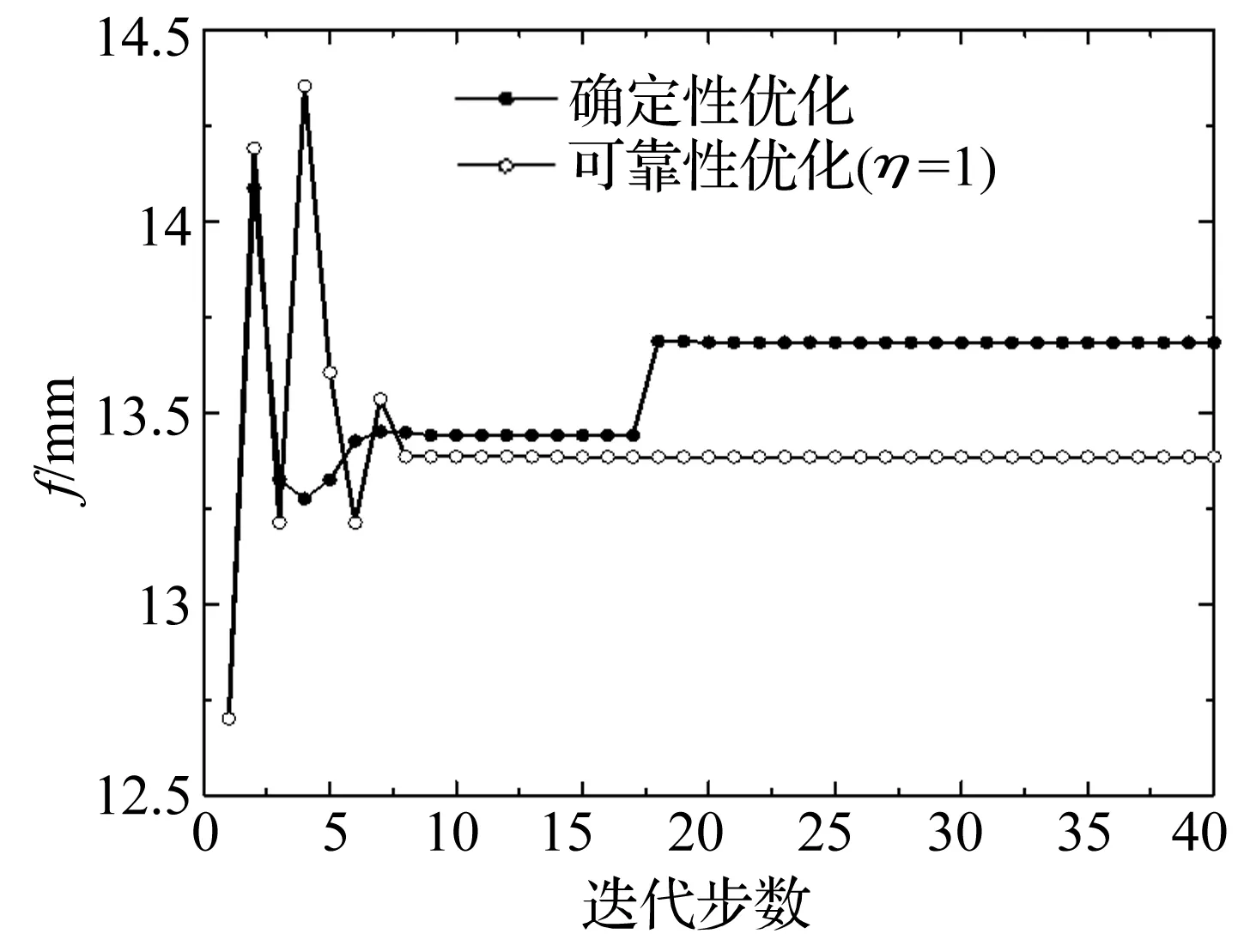
图11 半波高f的迭代曲线Fig.11 Iterative curves of semi-wave heightf

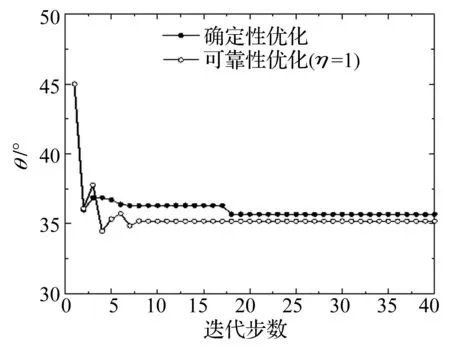
图12 梯形截面倾角θ的迭代曲线Fig.12 Iterative curves of trapezoidal dip angleθ

从图13可以看出，利用区间可靠度为1的优化方法能够使波纹板结构总质量从最初的3.938 kg下降到3.81 kg，与安全因子为1.1的确定性优化方法相比，可以获得更加明显的减重效果。其原因是区间可靠性优化方法在设计阶段利用区间向量对材料属性及外载荷中存在的不确定性进行了定量化表征，并从传播分析角度研究了不确定因素对结构可靠性的影响，以最大限度地发挥结构的安全承载能力。

在不同约束条件可靠性指标下的优化结果如表4所示。观察表4可以发现，当可靠性指标约束小于1，即波纹板能够容忍某种程度的屈曲失效时，区间可靠性优化方法与确定性优化方法相比获得的减重效果更加显著。但是，在不同的可靠度要求下，优化结果之间存在明显差异。当可靠度η=1.0时，波纹板结构的质量为3.811 kg；当可靠度η=0.9时，可以获得的最优结构质量为3.789 kg。

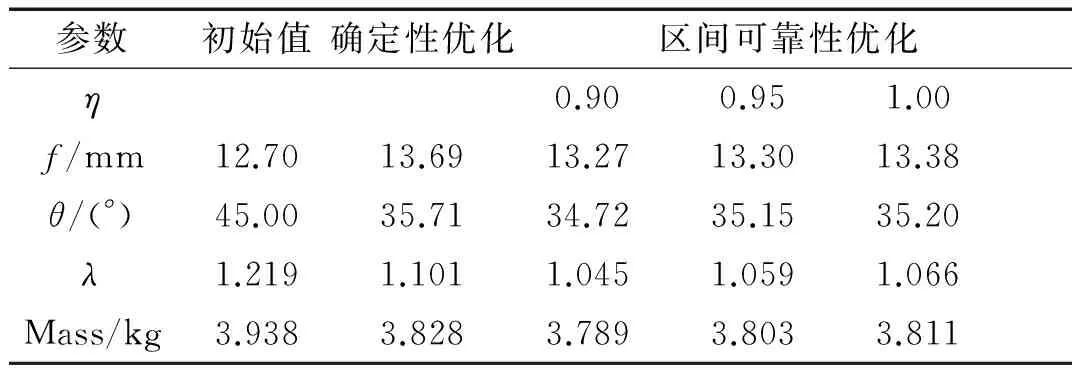
表4 区间可靠性优化与确定性优化结果比较

由此可见，当可靠性指标约束较低时，优化后得到的波纹板质量较轻，相反，随着可靠性指标约束的提高，波纹板结构质量也随之增加，即约束可靠性与目标函数性能之间是相互矛盾的。在复合材料波纹板的实际应用中，设计者可以权衡目标性能与可靠性之间的关系，根据安全性要求和偏好特点权衡优化方案。

5 结 论

(1) 通过理论推导得到的复合材料波纹板临界剪切屈曲载荷的计算结果与有限元分析结果吻合较好。

(2) 将区间参数顶点法与屈曲载荷的计算方法相结合，实现了屈曲载荷因子上下界的快速预估。充分考虑复合材料属性参数及外载荷中存在的不确定性对约束条件的影响，建立了区间可靠性优化模型，克服了传统嵌套优化计算效率低下的问题。

(3) 梯形波纹板外形参数的优化结果表明，由于区间可靠性优化方法在模型建立阶段就考虑了不确定因素的影响，与基于安全因子的确定性优化方法相比，在保证结构安全可靠的同时，利用不确定性带来的潜在优势，可以取得更好的减重效果。另外，当可靠性指标要求较高时，需要牺牲一定的目标性能。

[1] STROUD W J. Elastic constants for bending and twisting of corrugation-stiffened panels [R]. NASA TR R-166,Hampton: NASA Langley Research Center, 1963.

[2] BRIASSOULIS D. Equivalent orthotropic properties of corrugated sheets [J]. Computers and Structures,1986,23(2): 129-138.

[3] SAMANTA A, MUKHOPADHYAY M. Finite element static and dynamic analyses of folded plates [J]. Engineering Structures, 1999, 21: 277-287.

[4] YOKOZEKI T, TAKEDA S, OGASAWARA T,et al. Mechanical properties of corrugated composites for candidate materials of flexible wing structures[J]. Composites, 2006,37:1578-1586.

[5] XIA Y, FRISWELL M I, SAAVEDRA FLORES E I. Equivalent models of corrugated panels [J]. International Journal of Solids Structures, 2012, 49(13): 1453-1462.

[6] LIEW K M, PENG L X, KITIPORNCHAI S. Buckling analysis of corrugated plates using a mesh-free Galerkin method based on the first-order shear deformation theory [J]. Computational Mechanics, 2006, 38(1): 61-75.

[7] WENNBERG D, WENNHAGE P, STICHEL S. Orthotropic models of corrugated sheets in finite element analysis[J]. ISRN Mechanical Engineering, 2011: 1-9.

[8] SHAW A D, DAYYANI I, FRISWELL M I. Optimisation of composite corrugated skins for buckling in morphing aircraft [J]. Composite Structures, 2015, 119: 227-237.

[9] 吴存利, 段世慧, 李新祥. 复合材料波纹板剪切载荷作用下的屈曲试验与分析[J]. 航空学报,2011,32(8):1453-1460.

WU Cunli, DUAN Shihui, LI Xinxiang. Buckling investigation of composite corrugated panel subject to shear loads [J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1453-1460.

[10] TSAO C C, HOCHENG H. Effects of exit back-up on delamination in drilling composite materials using a saw and a core drill [J]. International Journal of Machine Tools and Manufacture, 2005, 45: 1261-1270.

[11] TEWARY V K. Mechanics of Fiber Composites [M]. New York: Wiley, 1978.

[12] JIANG C, HAN X, LIU G P. Uncertain optimization of composite laminated using a nonlinear interval number programming method[J]. Computers and Structures, 2008, 86: 1696-1703.

[13] 许孟辉, 邱志平. 复合材料点阵夹芯结构平压性能不确定分析与优化 [J]. 复合材料学报, 2013,30(4):177-184.

XU Menghui, QIU Zhiping.Uncertain analysis and optimization of compressive property of all-composite lattice truss core sandwich structure [J]. Acta Materiae Compositae Sinica, 2013, 30(4): 177-184.

[14] YI J, GIL H, YOUM K, et al.Interactive shear buckling behavior of trapezoidally corrugated steel webs [J]. Engineering Structure, 2008, 30(6): 1659-1666.

[15] KASSAPOGLOU C. Design and analysis of composite structures: With applications to aerospace structures [M]. Chicester: John Wiley & Sons, 2010.

[16] 袁坚锋,尼早,陈宝兴. 弯剪复合载荷作用下复合材料层合板的强度校核方法[J]. 复合材料学报,2014,31(1):234-240.

YUAN Jianfeng, NI Zao, CHEN Baoxing. Stress analysis of the buckling of composite laminates under bending shear combination loads [J]. Acta Materiae Compositae Sinica, 2014,31(1):234-240.[17] 佟强. 多项式实根求解[D]. 北京:清华大学, 2007.

[18] QIU Zhiping, WANG Xiaojun. Solution theorems for the standard eigenvalue problem of structures with uncertain-but-bounded parameters [J]. Journal of Vibration and Sound, 2005,282(1/2):381-399.

[19] 张全, 樊治平, 潘德惠. 不确定性多属性决策中区间数的一种排序方法[J]. 系统工程理论与实践,1999,5:129-133.

ZHANG Quan, FAN Zhiping, PAN Dehui. A banking approach for interval numbers in uncertain multiple attribute decision making problems[J]. Systems Engineering-Theory and Practice, 1999, 5: 129-133.

Bucklingperformance analysis and reliability optimization of composite corrugated plates under shear loading

ZHENG Yuning1, QIU Zhiping1, YUAN Kaihua2

(1. School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China;2. Beijing Institute of Machine and Electron, Beijing 100074, China)

Composite corrugated plates are widely used in wall webs of aircraft wings and their buckling reliability under shear loading is a key factor to be considered during the design of corrugated plates. Based on their equivalent models with flexural and tensional rigidities, a computation method for critical shear buckling loads of composite corrugated plates was derived by utilizing Ritz method and the principle of minimum potential energy. The uncertainties in composite structural parameters and external load were fully considered and quantified with interval vectors. By means of the vertex solution theorem, the response ranges of buckling factors were predicted and the interval analysis method of buckling reliability under shear loading was proposed. The interval possible level was adopted to describe the reliability of shear buckling. An interval reliability optimization model containing effects of parametric uncertainties was proposed for composite corrugated plates. Numerical examples indicated that the results with the proposed method and those with FEM agree well and the optimal results verifies the effectiveness of the proposed interval reliability optimization model and algorithm.

composite materials; corrugated plate; buckling; uncertainty; interval analysis; reliability optimization

国家自然科学基金项目(11432002);国防基础科研计划项目(A0420132101;JCKY2013601B001;A0820132001);高等学校学科创新引智计划项目(B07009)

2015-05-12 修改稿收到日期：2015-08-23

郑宇宁 男，博士生，1990年9月生

邱志平 男，博士，教授，1962年2月生

V214.8；TB332

A

10.13465/j.cnki.jvs.2016.19.002