Optimum blade loading for a powered rotor in descent

Ramin Modarres,David A.Peters

Department of Mechanical Engineeringamp;Materials Science,Washington University in St.Louis,St.Louis,MO 63130,USA

Optimum blade loading for a powered rotor in descent

Ramin Modarres*,David A.Peters

Department of Mechanical Engineeringamp;Materials Science,Washington University in St.Louis,St.Louis,MO 63130,USA

The optimum loading for rotors has previously been found for hover,climb and wind turbine conditions;but,up to now,no one has determined the optimum rotor loading in descent.This could be an important design consideration for rotary-wing parachutes and low-speed descents.In this paper,the optimal loading for a powered rotor in descent is found from momentum theory based on a variational principle.This loading is compared with the optimal loading for a rotor in hover or climb and with the Betz rotor loading(which is optimum for a lightly-loaded rotor).Wake contraction for each of the various loadings is also presented.

1.Introduction

A problem of long-standing interest in rotor and propeller theory has been determination of the optimum blade loading for a rotor(i.e.,the loading that gives minimum power for a given thrust).Glauert's second approximation to momentum theory allows him to invoke a variational principal to obtain the optimality condition for a rotor in hover.1He also works out a numerical approximation.1Glauert's minimum power is demonstrated in Ref.1to be slightly lower than the power due to the Betz loading.2Ref.3demonstrates that Glauert's variational principle for hover can be cast as a cubic equationin the unknown loading that has a compact,closed-form solution for the optimum blade loading in hover(as based on momentum theory).

Ref.4offers a third approximation to Glauert's momentum equations.This third approximation gives the same optimality condition as does Glauert's second approximation,but it allows development of wake contraction equations-valid in hover and climb-to give downstream variables due to an arbitrary loading distribution.Applications are given in Ref.4for the Betz loading distribution.Ref.4also demonstrates that,for powered rotors in descent,the Betz loading always results in some portions of the rotor being in either wind-turbine state or vortex-ring state.Thus,solution of the contraction equations with a Betz distribution is not possible for descent.It is further found in Ref.4that-beyond a critical descent rateno portion of a Betz-loaded rotor is in a working state(i.e.,momentum theory breaks down over the entire span,and one enters the vortex-ring region from the helicopter side).This critical descent rate with the Betz distribution is shown to be the same descent rate predicted by the vortex theory of Wolkovitch.5

Ref.6reveals that Glauert's variational principal for optimum loading can be extended to the case of general climb or descent rate and leads to a quartic equation in the unknown loading.Optimum solutions based on numerical solution of the quartic are given in Ref.6for the cases of hover and climb-but not for descent.In this paper,we solve this quartic equation to find the optimum loading for a powered rotor in descent and then compute the wake contraction due to this loading.It will be shown that the optimum loading decreases to zero as the rotor approaches the wind-turbine vortex-ring boundary such that vortex-ring state is not encountered when the rotor is optimized.

Glauert's second approximation to momentum theory implies that the induced flow at the rotor disk is parallel to the local thrust vector4:

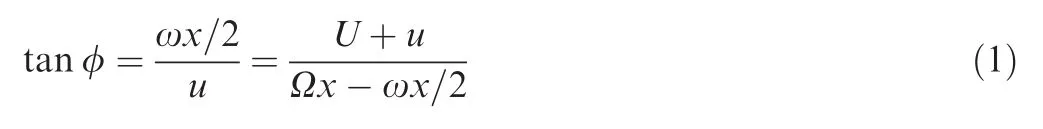
where φ is the angle of inflow and thrust vector,ω the wake rotational speed,x the radial coordinate,u the induced flow at rotor,U the climb rate and Ω the rotor singular speed.From Eq.(1),u can be written in terms of ω(or vice versa).The incremental thrust dT and incremental power dP at a radial station thus become:

One can adjoin the thrust to the power with a Lagrange multiplier Λ and obtain a variational statement for the minimum induced power PIgiven a specified thrust.

where J is the power functional and δ(.)the variational operator.This variational statement for power results in a quartic equation for the optimum angular velocity ω at any radial location-from which one can find the optimum u and the optimum loading,dT/dr6:

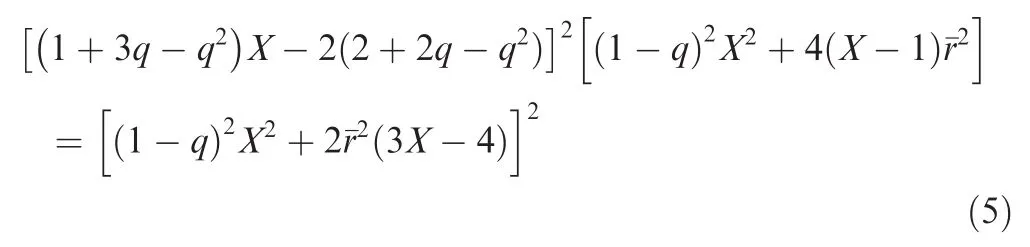
with

where R is the rotor radius,q the normalized loading parameter,q the nondimensional climb rate(η =U/(ΩR))and ν0the nondimensional Lagrange multiplier-which becomes the Glauert loading parameter.Once Eq.(5)is solved forEq.(1)can be used to find ω,u,and the bound circulation of the optimum loading Γ:

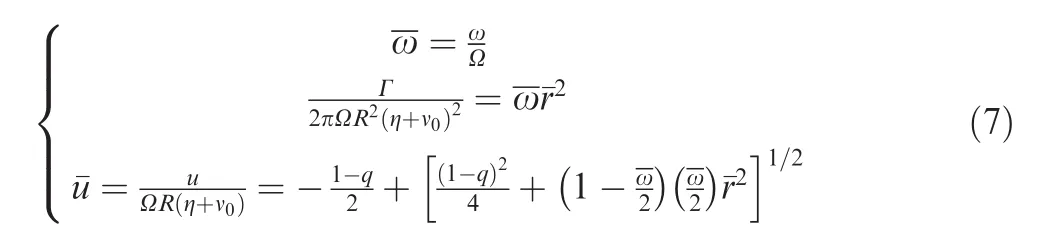
Therefore,solution of the quartic Eq.(5)gives the entire solution for an optimum rotor in climb,hover,or descent.The optimum thrust and power are determined by Eqs.(2)and(3).

where CTis the thrust coefficient(T/(ρπR2Ω2R2))and CPis the power coefficient(P/(ρπR2Ω3R3)).Eqs(5)–(9)are suff icient to describe the optimum rotor in hover,climb,or descent under Glauert's second approximation to momentum theory.For hover,q=1;for climb,0lt;qlt;1;and,for descent,qgt;1.Thus,the above equations give a normalized form of the optimum rotor for all powered states.

2.Solution method

For hover(η=0,q=1),Eq.(4)reduces to a cubic in X which can be solved in closed form for the unknown X and,consequently,for ω.As shown in Ref.3,that cubic has a compact closed form solution.

where

For rotors in climb or descent,one must deal with the entire quartic in Eq.(5).Although there is a closed form solution to the quartic,it is quite cumbersome.For computational purposes,the most ef ficient approach is to solve Eq.(5)numerically for any given value of q andThere are four numerical roots for each case,but the physically meaningful root is always the smallest,positive-real value for

It will be interesting to compare this optimum solution with the Betz loading,the latter of which can be expressed as:

where qBis the Betz loading parameter.Later,we will make this comparison.However,it should first be noted that,in the Betz loading in Eq.(12),the loading parameter qBis based on the Betz loading variable ν0,qB= ν0/(η + ν0),where for Betz the parameter ν0is equal to ν∞(the induced flow for large r).In contrast,the parameter ν0used to de fine q andin Eqs.(5)and(6)is only equal to the far- field induced flow for q=0 and q=1.The parameter ν0varies slightly from ν∞in the range 0lt;qlt;1 and varies substantially for qgt;1.5.Later,we will give the exact correspondence between the values of qBand q for Betz and for the Glauert optimum.

Either the optimum or the Betz solution can be placed into Eqs.(7)–(9)to obtain the loading and in flow.For small q,the Glauert solution approaches the Betz solution.Note,also,that in the Betz loading in Eq.(12),is invariant with q,such that all climb rates have the same normalized value ofFor this reason,we will comparebetween the optimum and the Betz loadings such that q=0 curve for the optimum loading will exactly equal the Betz result for all loadings.

As noted in Ref.4,there is a differential equation that leads to the contraction ratio K for any loading under the third approximation to Glauert momentum theory:

wherefis the contraction function and K the ratio of a far downstream radius of a stream line to the radius of that streamline at the rotor disk.The numerical solution of Eqs.(4)–(9)-described above-can be substituted into Eqs.(13)and(14)which is then solved numerically to give the contraction ratio for either the Betz or the optimum loading at any loading parameter q.

3.Numerical results

Because blade circulation is zero at the blade root-whereas wake rotation is zero for large normalized radius-it is instructive to consider wake rotation near the blade root and blade circulation far away from the root.Fig.1 presents the roots for(at the root)as a function of q,as found from Eq.(5)atthe quartic degenerates into a quadratic so that two roots forbecome in finite and there are only two finite roots-as shown in the figure.As q approaches 0,an in finitesimal loading,the smallest root forapproaches 2q(which is also the Betz loading).As loading increases,the smallest positiveincreases until it reaches a value of 1.0 at hover,q=1.This is in agreement with the closed-form solution in Eq.(10).For 1lt;qlt;2.732,which is descent,the smallest positive root no longer changes with q,but remains fixed atThis behavior at the root is an indicator that the optimum rotor loading in descent will be qualitatively different than the optimum loading in climb.For qgt;2.732,one of the roots becomes negative,which is an indication of the passage into the wind-turbine vortex-ring region,for which momentum theory is not valid.In that region,there is no positive root to the quartic for whichdecays to zero in the far field.

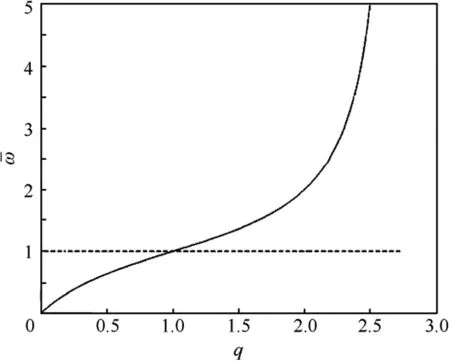
Fig.1 Roots of quartic atfor various values of rotor state parameter q.

Fig.2 gives the solution forversus q in the limit asr goes to in finity.HereΓ is the circulation normalized on in flowNote that,in climb(0lt;qlt;1),the circulation is close to 2q(the Betz value);but,for descent(qgt;1),the circulation drops as the wind turbine region approaches at q=2.732.This implies that,as the wind-turbine,vortex-ring region is approached,the optimum rotor(which,by de finition must avoid vortex-ring state)gradually decreases blade loading until the''optimumquot;rotor at the boundary becomes unloaded.

Now that Figs.1 and 2 have presented the optimum loading both near the root and far from the root,we can turn to look at the optimum loading over the entire blade.Since rotation is more instructive near the root(while circulation is more instructive far from the root),Figs.3 and 4 give both the optimum wake rotation,and the optimum circulation,respectively.is the circulation normalized on ν∞(η + ν∞)for better comparison with BetzBoth quantities are presented versusand at various values of q.Recall that the q=0 curve in either figure represents the Betz value for all values of q(i.e.,for all loadings in both climb and descent).From Fig.3,one can see that-as was pointed out from Fig.1-the optimum root circulation in descent moves from 2.0(the Betz value)to 1.0 as the descent rate decreases to zero(i.e.,as q moves from 0 to 1.0,hover).For descent,the root value ofis fixed at 1.0 such thatin descent.

Fig.4 indicates that the blade circulation for all values of q approaches the same far- field value(asapproaches∞)of Γ=2.0,which is the optimum value when wake rotation is small.Another interesting aspect of Fig.4 is the way that the circulation changes from the lightly-loaded case(q=0)to the hover case(q=1)and then tends to move back toward the lightly-loaded case as descent is increased.This is because,as we saw in Fig.2,the optimum rotor must become increasingly unloaded as q is increased,thus approaching an unloaded condition at q=2.732.

At this point it is good to find the equivalent values of ν∞and qBfor the optimum distributions presented herein.Based on Fig.2,which gives the loading at large normalized radius,one can find the induced flow at large radius.This gives:

Fig.2 Circulation in limit as approaches in finity a function of q.

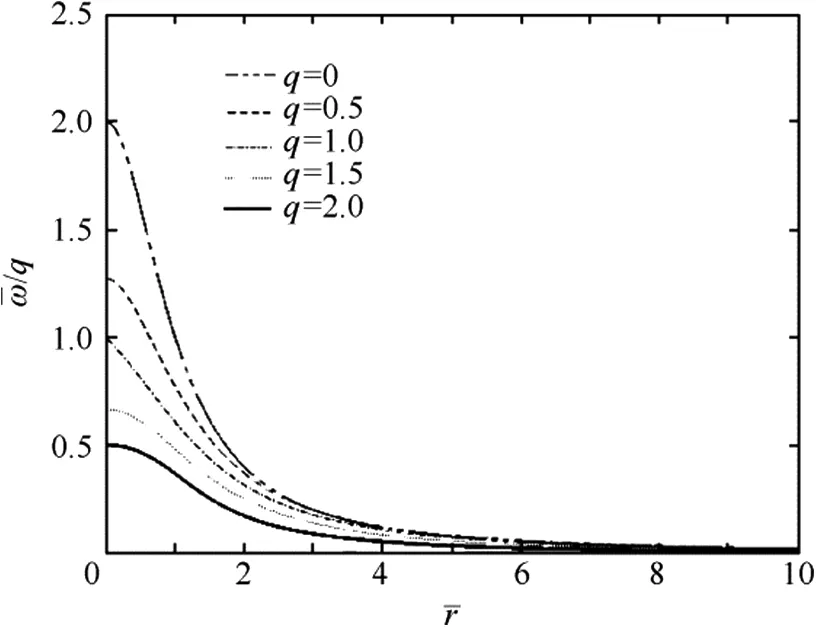
Fig.3 Solution of quartic equation for optimum wake rotation in climb and descent.

Fig.4 Solution of quartic equation for optimum blade loading in climb and descent.

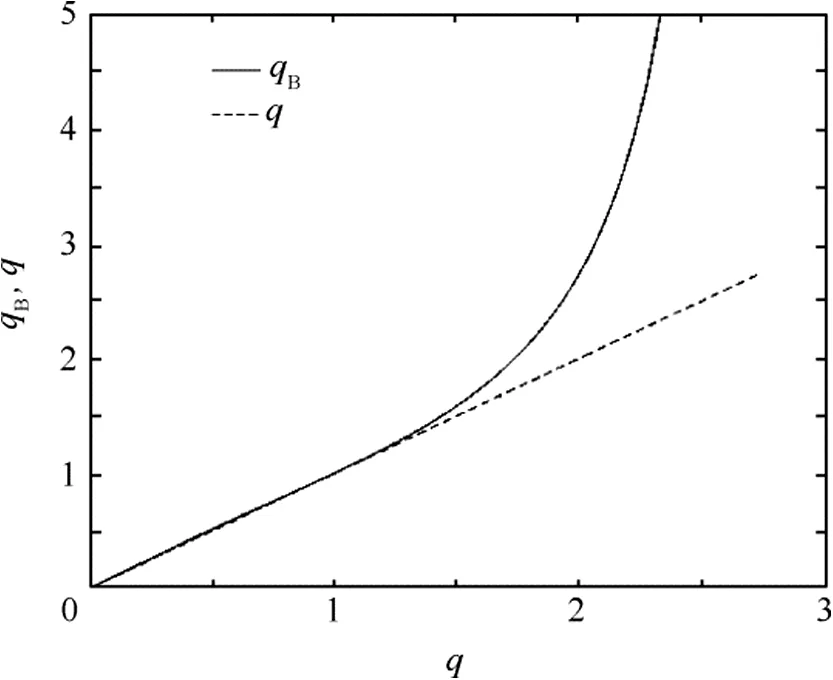
Fig.5 Equivalence of Betz and Glauert loading parameters.

Fig.6 Rotor regions as a function of q plotted on Gessow and Meyers normalized momentum plot.7

Fig.7 Contraction ratio vs normalized radial position for optimum loading.

Fig.5 presents the equivalent Betz qBas a function of the present q.The two are identical for lightly loaded(q=0)and for hover(q=1).For the climb rates between,they are very close-with a maximum difference of 3%at q=0.5,qB=0.516.However,for descent(qgt;1)the two begin to diverge with the divergence accelerating as the system approaches the transition into the windmill vortex-ring state at qB=∞(see Fig.5)occurring at q=2.732(as seen in Figs.1 and 2).

Fig.6 shows the various momentum regions plotted on the momentum theory figure from Ref.7with boundaries based on the Betz definition,qB= ν∞/(η+ ν∞).For the Betz distribution,the transition to vortex-ring state from the helicopter side occurs at qB=2,which is equivalent to q=1.737 for the Glauert definition of q.However,the optimum loading from Glauert avoids vortex-ring state(as q approaches infinity)by lowering the loading with q until the loading is zero at the wind-turbine boundary.In a similar manner,the wind turbine region is entered when the Betz q is equal to+∞(the case for which η =-ν0).In contrast,the induced flow is equal to the climb rate for the optimum distribution when the q based on the Glauert ν0is equal to 2.732.

Fig.7 presents the contraction functionat various values of q for the optimum loading.Note that in the case of climb,it is the case that K(0)=1.0(0lt;qlt;1),whereas,for descent,K(0)=0(1lt;qlt;2.732).The fact that K(0)=0 in descent implies a concentration of vorticity into a root vortex as streamlines are forced toward the rotor center.The case of hover is the singular case between the two with a value of K(0)=0.3872.The singular behavior can be seen as q approaches 1.0 from either the climb side or the descent side(q=0.9 and q=1.1,respectively).

4.Conclusions

(1)Application of a variational principle to Glauert's momentum theory gives a quartic equation for the optimum loading for a powered rotor in descent,which has never before been published.

(2)Numerical solution of that equation shows that,for the optimal loading in descent(ηlt;0),momentum theory breaks down at q= ν0/(ν0+ η)=2.372 which is the transition into the wind-turbine vortex-ring region.

(3)Wake contraction is computed for the optimum loading at various values of climb and descent rates.Wake contraction curves begin at the rotor center with K(0)=1.0 for climb and with K(0)=0 for descent,with hover being the singular solution that bounds the two regions with K(0)=0.3872.

Acknowledgments

This work was sponsored by the GT/WU Rotorcraft Center of Excellence Program,Dr.Mahendra Bhagwat,technical monitor.

1.Glauert H.Airplane propellers.In:Durand WF,Glauert H,editors.Aerodynamic theory.New York:Dover Publications;1980.p.251-8–310-4.

2.Betz A,Prandtl L.Schrauben propeller mit geringstem energieverslust.Goettinger Nachrichten 1919;3:193–217.

3.Modarres R,Peters DA.Optimum actuator-disk performance in hover and axial flight by a compact momentum theory with swirl.J Am Helicopter Soc 2015;60(1):1–10.

4.Peters DA,Modarres R,Howard AB,Rahming B.Solution of Glauert's contraction/expansion equations for wind turbines and powered rotors with swirl.The 70th annual national forum of the American Helicopter Society.Alexandria:The AHS International,Inc.;2014.

5.Wolkovitch J.Analytic prediction of vortex-ring boundaries for helicopters in steep descents.J Am Helicopter Soc 1972;17(3):13–9.

6.Modarres R,Williamn L,Rahming B,Peters DA.Closed-form solutions for the optimum rotor in hover and climb,Proceeding of the 42ndEuropean Rotorcraft Forum,Lille,France,September 5–8;2016.

7.Gessow A,Meyers Jr GC.Aerodynamics of the helicopter.New York:The MacMillan Company;1952,p.131.

Ramin Modarresis a Ph.D.candidate at the Center for Computational Mechanics of Washington University in St.Louis.His research area is the helicopter aerodynamics.

David A.Petersis the McDonnell Douglas professor of engineering at Washington University and associate director of the Georgia Tech/Washington University Center of excellence for rotorcraft.He has received his B.S.and M.S.degrees in applied mechanics from Washington University in St.Louis in 1969 and 1970,and then his Ph.D.degree in aeronautics and astronautics from Stanford University in 1974.He has worked at McDonnell Douglas,the Army Research Labs,Georgia Tech,and Washington University.He has also served as editor-in-chief of the Journal of the American Helicopter Society and is presently a member of the Board of Directors of the American Helicopter Society.He has been awarded with the Nikolsky Lecture by AHS,the Reed Aeronautics Award by AIAA,and the Spirit of St.Louis Medal by ASME.

13 February 2016;revised 18 February 2016;accepted 22 February 2016

Available online 9 May 2016

Descent;

Helicopter;

Inflow;

Loading;

Optimum

Ⓒ2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.

E-mail addresses:ramin.modarres@wustl.edu(R.Modarres),dap@wustl.edu(D.A.Peters).

Peer review under responsibility of Editorial Committee of CJA.