基于线性回归分析方法的厦门市住宅需求量预测
黄 嘉 仪
(厦门工学院,福建 厦门 361021)
基于线性回归分析方法的厦门市住宅需求量预测
黄 嘉 仪
(厦门工学院,福建 厦门 361021)
以厦门市为研究对象,运用线性回归分析法,分析了影响该市住宅需求量的因素,从居民可支配收入、房地产价格、常住人口三方面,预测了该市的住宅需求量,对厦门市住房市场的发展有一定的意义。
住宅需求量,线性回归分析,房地产价格,常住人口
住宅需求供应关系研究的基础是住宅需求量预测研究,它的数据是政府平衡住宅供给的数据基础。在本文中具体的研究方法是根据厦门市历史数据和目前现状,结合人口的变化和经济增长变化,运用线性回归分析的方法,为今后厦门城市住宅市场建立数学模型进行分析和预测,并通过相应的数学方法,为厦门市未来住宅需求量进行总结,因此对厦门市住房市场的发展具有一定的指导作用。
1 线性回归分析的数学模型简介
一个自变量与因变量的线性关系可以由一个数学方程表达出,即一元线性回归方程,记作Y′=a+bx(a,b确定)。
一元线性回归模型为:
Y=β1X+β2+ε
(1)
ε~N(0,σ2)。
其中,X为自变量;ε为除了自变量外其他的因素对因变量的影响,由式(1)可以得到:
Y~N(β1X+β2,σ2)
(2)
称Y的条件期望E(Y|X)=β1X+β2为Y对X的回归。
设(yi,xi),i=1,2,…,N为对样本观察值,则一元线性回归有如下数据结构:
yi=β1xi+β2+εi,i=1,2,…,N
(3)
εi~N(0,σ2),且相互独立。
本文中不考虑其他因素对因变量的影响,只考虑单因素的影响。我们所要计算的参数就是方程中的β1和β2。
由于回归分析的计算量极大,使用手工计算非常繁琐,因此需要用到回归分析的Microsoft Excel软件求解方法。
2 住宅需求量影响因素分析
针对影响住宅需求量的因素,在参考了一些文献后,选取了三个具有代表性的影响因素即:城镇居民可支配收入、房价、城市常住人口。
2.1 厦门市城镇居民可支配收入对住宅需求量影响分析
厦门市经济的快速发展导致厦门市人均可支配收入每年都在以一定的比例增长。从有关资料中可以查出2003年,厦门市居民可支配收入12 915.12;2013年,厦门市居民可支配收入41 360.40,相比10年前增长了快3倍,年平均增长率达到12.35%。
与此同时,厦门市住宅销售面积也跟着逐年增长。从2003年的1 867 448 m2的销售面积增长到2013年的6 153 435 m2的销售面积,比2003增长近3倍,年平均增长率达到12.67%。历年城镇居民生活收支情况见表1。
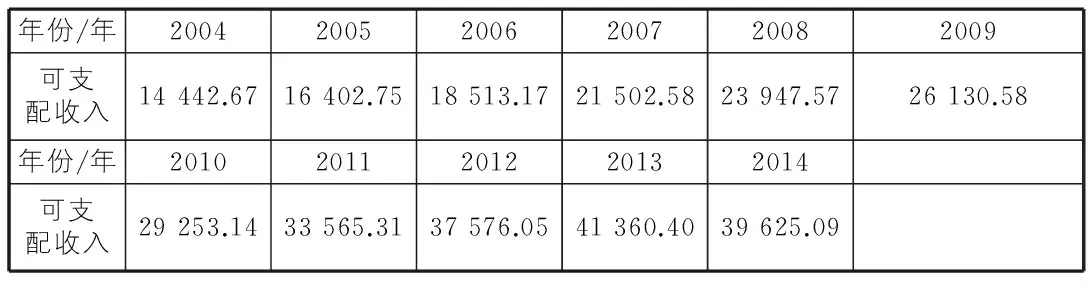
表1 历年城镇居民生活收支情况
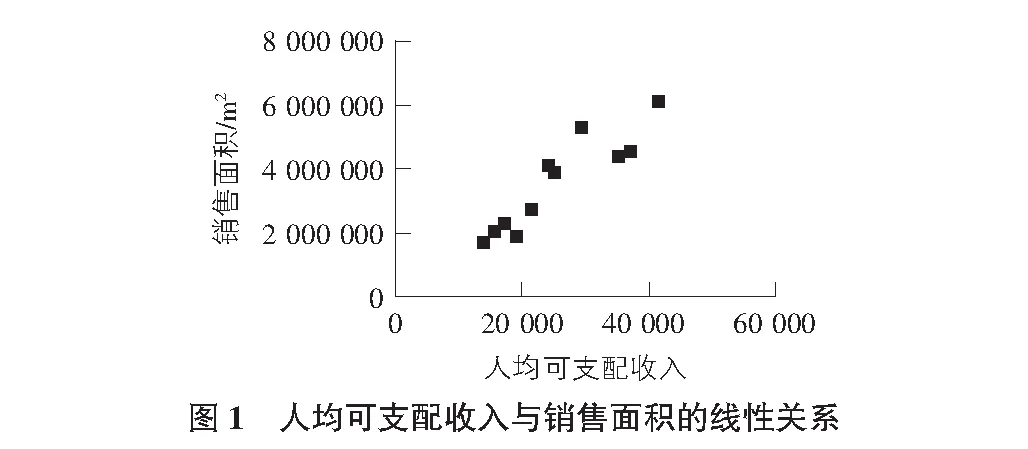
由图1可猜测厦门市居民人均可支配收入与住宅销售面积之间存在正线性相关关系。
为验证猜测可信度,本文使用Excel软件进行线性回归分析,结果如图2所示。
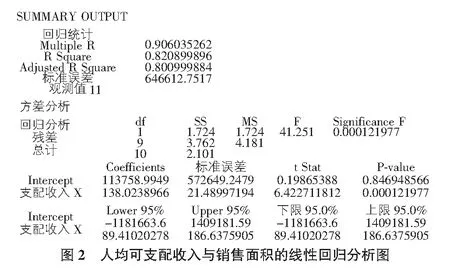
由图2的输出结果,可得到回归系数为β1=138,β2=113 759。
故所求回归方程为:Y=138X+113 759。
即厦门市居民可支配收入增加1元,年住宅销售面积将增加138 m2。再由图2可知相关系数(Multiple R)为0.906>0.8。即城镇居民可支配收入与住宅销售面积具有高度相关性。
2.1.1 线性关系的检验
由图2可知用于检验的显著性F,即Significance F,它就是用于检验的P值。将“Significance F”的值与给定的显著性水平α的值进行比较(显著水平α=0.05)。当Significance F<α,则表明因变量Y与自变量X之间有显著的线性关系;如果Significance F>α,则没有证据表明因变量Y与自变量X之间有显著的关系。在图2输出的结果中,Significance F=0.000 121 977<α=0.05,这说明住宅销售面积与厦门市城镇居民可支配收入之间存在显著的线性关系,所得结论与统计量检验相同。
2.1.2 回归系数的检验
回归系数的显著性检验就是检验回归系数β1是否等于0。图2中除了给出检验的统计量,还给出了用于检验的P值(P-value)。当P-value<α,则表明因变量Y与自变量X之间有显著的线性关系;如果P-value>α,则没有证据表明因变量Y与自变量X之间有显著的关系。由Excel得出的图2中可以知道P-value=0.000 121 977<α=0.05,这说明住宅销售面积与厦门市城镇居民可支配收入之间存在显著的线性关系,所得结论与统计量检验相同。
2.2 厦门市房地产价格对住宅需求量影响分析
历年房价与住宅销售面积情况见表2。

表2 历年房价与住宅销售面积情况
利用Microsoft Excel软件绘制以住宅销售面积为Y轴,厦门市房价为X轴的散点图,分析住宅销售面积与房价的相关性。
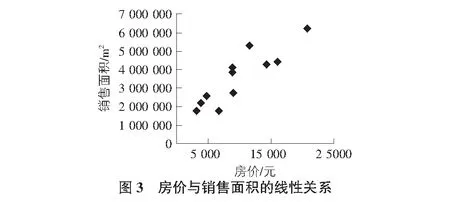
由图3可猜测厦门市房价与住宅销售面积之间存在正线性相关关系。为验证猜测可信度,本文使用Excel软件进行线性回归分析,结果如图4所示。
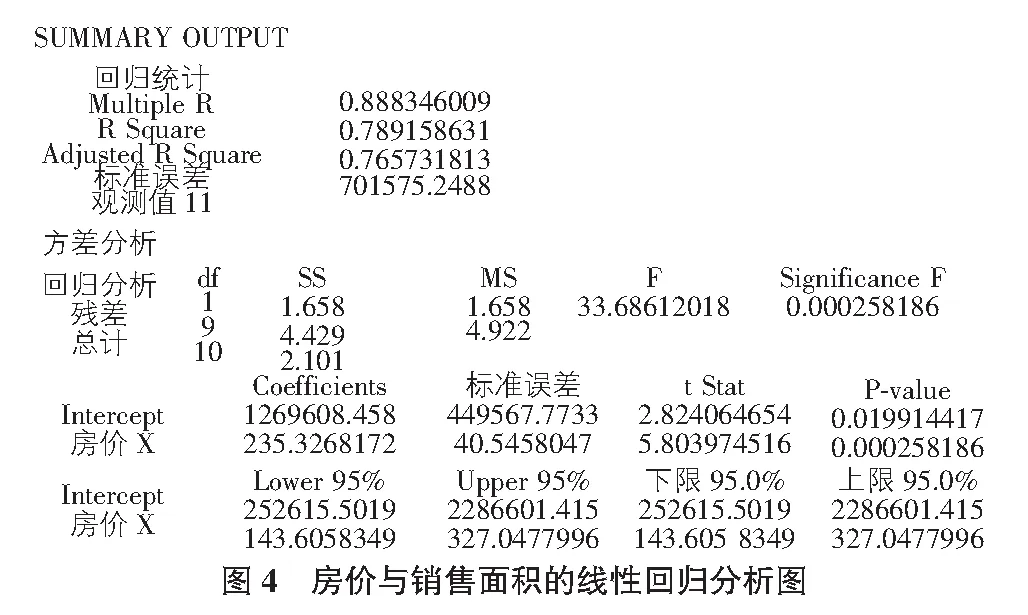
由图4的输出结果,可得到回归系数为:
β1=235.3,β2=1 269 608。
故所求回归方程为:
Y=235.3X+1 269 608。
即厦门市房价提高1元,年住宅销售面积将增加235.3 m2。再由图4可知相关系数(Multiple R)为0.888>0.8,即厦门市房价与住宅销售面积具有高度相关性。
2.2.1 线性关系的检验
由图4中可知用于检验的显著性F,即Significance F,它就是用于检验的P值。将“Significance F”的值与给定的显著性水平α的值进行比较(显著水平α=0.05)。当Significance F<α,则表明因变量Y与自变量X之间有显著的线性关系;如果Significance F>α,则没有证据表明因变量Y与自变量X之间有显著的关系。在图4的输出的结果中,Significance F=0.000 258 186<α=0.05,这说明住宅销售面积与厦门市房价之间存在显著的线性关系,所得到的结论与统计量的检验一致。
2.2.2 回归系数的检验
回归系数的显著性检验就是检验回归系数β1是否等于0。图4中除了给出检验的统计量,还给出了用于检验的P值(P-value)。检验时可直接将P-value与给定的显著性水平α进行比较。当P-value<α,则表明因变量Y与自变量X之间有显著的线性关系;如果P-value>α,则没有证据表明因变量Y与自变量X之间有显著的关系。由图4可知P-value=0.000 258 186<α=0.05,这说明住宅销售面积与厦门市房价之间存在显著的线性关系,所得结论与统计量检验相同。
2.3 厦门市常住人口对住宅需求量影响分析
2013年为止,厦门市的人口有373万人,比2003年的245万人增多了128万人,增长了62.3%,每年增长率接近5.01%,明显比全省范围内的城市人口增长率高的多。因此,厦门市也成为福建省人口第四多的城市。人口的快速增长也导致厦门市居民住宅需求量的变化。历年厦门市人口与年住宅销售面积情况如表3所示。
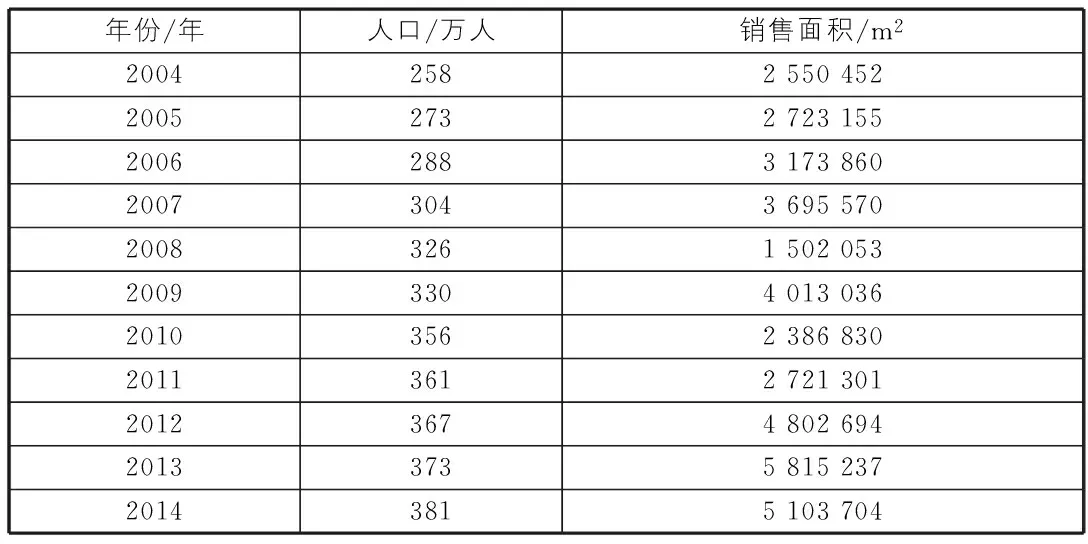
表3 历年厦门市人口与年住宅销售面积情况
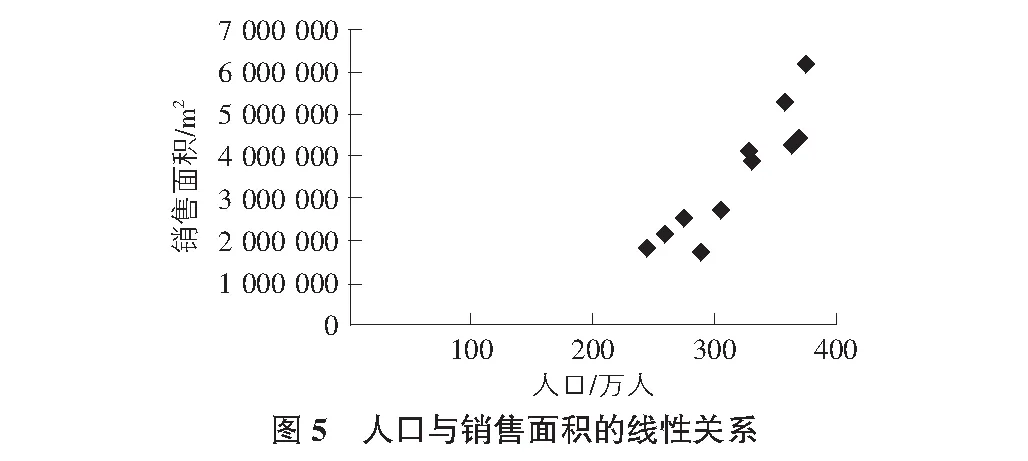
利用Microsoft Excel软件绘制以住宅销售面积为Y轴,厦门市人口为X轴的散点图,分析住宅销售面积与常住人口的相关性。
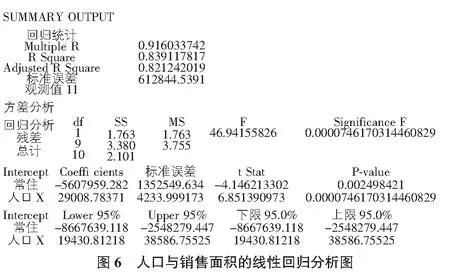
由图5可猜测厦门市人口与住宅销售面积之间存在正线性相关关系。为验证猜测可信度,本文使用Excel软件进行线性回归分析,结果如图6所示。
由图6的输出结果,可得到回归系数为:
β1=29 008.8,β2=-5 607 959。
故所求回归方程为:
Y=29 008.8X-5 607 959。
即厦门市常住人口增加1万人,年住宅销售面积将增加29 008.8 m2。再由图6可知相关系数(Multiple R)为0.916>0.8。即厦门市常住人口与住宅销售面积具有高度相关性。
2.3.1 线性关系的检验
由图6中可知用于检验的显著性F,即Significance F,它就是用于检验的P值。将“Significance F”的值与给定的显著性水平α的值进行比较(显著水平α=0.05)。当Significance F<α,则表明因变量Y与自变量X之间有显著的线性关系;如果Significance F>α,则没有证据表明因变量Y与自变量X之间有显著的关系。在Excel得出图6的输出的结果中,Significance F=0.000 074 617<α=0.05,这说明住宅销售面积与厦门市常住人口之间存在显著的线性关系,所得结论与统计量检验相同。
2.3.2 回归系数的检验
回归系数的显著性检验就是检验回归系数β1是否等于0。图6中除了给出检验的统计量,还给出了用于检验的P值(P-value)。检验时可直接将P-value与给定的显著性水平α进行比较。当P-value<α,则表明因变量Y与自变量X之间有显著的线性关系;如果P-value>α,则没有证据表明因变量Y与自变量X之间有显著的关系。由图6可知,P-value=0.000 074 617<α=0.05,这说明住宅销售面积与厦门市常住人口之间存在显著的线性关系,所得结论与统计量检验相同。
3 厦门市住宅市场需求量预测
3.1 基于居民可支配收入对未来几年厦门住宅需求量的预测
由前文可知2013年居民可支配收入为41 360.40元,年增长率为12.68%,可预测[8]未来三年的居民可支配收入:
2014年:41 360.40×(1+0.123 5)=46 468.41元。
2015年:46 468.41×(1+0.123 5)=52 207.26元。
2016年:52 207.26×(1+0.123 5)=58 654.86元。
将上式结果分别代入回归方程:
Y=138X+113 759。
即得各年住宅销售面积:
2014年:Y=138×46 468.41+113 759=6 526 399 m2。
2015年:Y=138×52 207.26+113 759=7 318 361 m2。
2016年:Y=138×58 654.86+113 759=8 208 130 m2。
3.2 基于房地产价格对未来几年厦门住宅需求量的预测
由数据可计算的从2003年至2013年房价年均增长率为20.6%,则可预测未来几年房价:
2014年:20 697.43×(1+0.206)=24 961.10元。
2015年:24 961.10×(1+0.206)=30 103.09元。
2016年:30 103.09×(1+0.206)=36 304.32元。
将上式结果分别代入回归方程:Y=235.3X+1 269 608。
即得各年住宅销售面积:
2014年:Y=235.3×24 961.10+1 269 608=7 142 955 m2。
2015年:Y=235.3×30 103.09+1 269 608=8 352 865 m2。
2016年:Y=235.3×36 304.32+1 269 608=9 812 014 m2。
3.3 基于常住人口对未来几年厦门住宅需求量的预测
由数据可知过去10年厦门市常住人口年增长率为5.57%,由此可预测未来几年厦门市常住人口数量:
2014年:373×(1+0.055 7)=394万人。
2015年:394×(1+0.055 7)=416万人。
2016年:416×(1+0.055 7)=439万人。
将上式结果分别代入回归方程:
Y=29 008.8X-5 607 959。
即得各年住宅销售面积:
2014年:Y=29 008.8×394-5 607 959=5 821 508 m2。
2015年:Y=29 008.8×416-5 607 959=6 459 702 m2。
2016年:Y=29 008.8×439-5 607 959=7 126 904 m2。
3.4 综合三个因素对未来几年厦门住宅需求量的预测
综合三个因素对未来几年厦门住宅需求量的预测,取三者平均值为预测,即:
2014年销售面积=(6 526 399+7 142 955+5 821 508)÷3=6 496 954 m2。
2015年销售面积=(7 318 361+8 352 865+6 459 702)÷3=7 376 976 m2。
2016年销售面积=(8 208 130+9 812 014+7 126 904)÷3=8 382 349 m2。
3.5 厦门市住宅需求量预测结果
经计算得到未来几年的厦门市住宅需求量的预测值,2014年厦门市的住宅需求量为6 496 964 m2;2015年厦门市的住宅需求量为7 376 976 m2;2016年厦门市的住宅需求量为8 382 349 m2。
4 结语
本文通过对厦门市住宅需求量影响因素定量和定性的分析,得到以下几个结论:
1)影响厦门市住宅需求量的因素很多,本文主要研究了以下三个因素:厦门市城镇居民可支配收入、厦门市房价以及厦门市常住人口数量。这三个因素与厦门市住宅需求量都存在正相关关系,并且影响比较大。2)通过线性回归分析,根据历史统计资料和获得的数学模型预测出厦门市2014年—2016年的住宅需求量分别为6 496 964 m2,7 376 976 m2,8 382 349 m2。3)本论文样本数据不完善。由于我国住宅市场形成和发展时间较短,数据资料统计不完全,所以无法收集到更多,更详细的有效资料,因此这会在一定程度上影响预测的准确性。4)社会在不同的经济发展阶段的情况下,人们对住宅存在不同层面上的需求,因此本文的结论并不是在任何情况下都可以成立。
[1] Abraham,J.M, P.H.Hendershott.Bubbles in Metropolitan Housing,Journal of Housing Research,2010:191-207.
[2] 王金明,高铁梅.对我国房地产需求和供给函数的动态分析[J].中国软科学,2011(4):12-16.
[3] 吴 群.供给关系对大都市商品住宅价格作用机理的分析——以南京市为例[J].中国土地科学,2010(2):51-56.
[4] 武秀丽,张 锋.时间序列分析法在住宅需求量预测中的应用——以广州市的数据为例[J].科学技术与工程,2011(21):26-29.
[5] 刘晓梅,汪雪梅,韩红丽.等维灰数递补MGM(1,n)模型在住宅需求量预测中的应用[J].西安建筑科技大学学报(自然科学版),2010(1):62-63.
Forecasting of housing demand in Xiamen based on linear regression analysis method
Huang Jiayi
(XiamenInstituteofTechnology,Xiamen361021,China)
Taking Xiamen as the research object, using the linear regression analysis method, this paper analyzed the factors influence of the city residential demand, from the residents’ disposable income, real estate prices, permanent residents population three aspects, predicted the city’s housing demand, had certain significance to the development of housing market in Xiamen.
housing demand, linear regression analysis, real estate price, permanent residents population
1009-6825(2016)10-0231-04
2016-01-22
黄嘉仪(1989- ),女,硕士,助教
F293.3
A
——与非适应性回归分析的比较

