高增益参量过程中相干态和真空态输入下的干涉光刻研究

韩 鹏，夏祎鸣，台运娇，许业军

(池州学院 机电工程学院，安徽 池州247000）

1 引言

半导体工业的发展使得人们需要特征尺寸越来越小的集成电路块，集成密度将直接制约器件的运行性能，因而就需要通过提高印刷术获得更大的分辨率，进而达到增加运算速率、降低功耗的效用。光刻技术就是适应这一生产需要被广泛运用的印刷术之一[1-2]。在过去的几十年里，集成电路的特征尺寸以平均每年约10%的速度减小[3]，然而，随着器件微型化程度越来越高，传统的经典光刻技术遭遇瑞利衍射极限难以突破的障碍，极大地制约了当前半导体制造技术的发展，使得光刻技术面临新的挑战。

近年来，开发光的量子特性打破经典衍射极限的量子干涉光刻技术已成为热门的研究领域[4-12]。量子光刻法最早有Boto等人（2000）首次提出，其研究表明：利用“N光子最大纠缠态”可以将光刻分辨率提高到经典情形的N倍[13]。例如：Agarwal研究小组（2001）在传统光刻装置中利用高增益参量放大器取代参量下转换器，所产生的关联双光束能有效地提高光子吸收率，但是以牺牲条纹可见度下降至接近20%作为代价[14]，这一过程后来被Sciarrino等（2008）在实验中所证实[15]；Gerry(2003)利用“弱对相干态”进行量子光刻，通过量子干涉调控有效地消除了背景项，并获得了约6倍于双光子NOON态所产生的曝光率[16]；湖南师范大学匡乐满研究组（2003）研究了N光子非最大纠缠态的量子光刻法[17]，提出了入射量子态的局域纠缠度和非局域纠缠度的概念；最近，东南大学龚彦晓（2013）利用“对相干态”进行N光子量子光刻研究[18]，并发现对相干态所获得的光刻性能一定程度上优于双模压缩真空态情形[19]。

本文选择利用高增益参量放大器取代传统光刻装置中的参量下转换器，并使用相干态和真空作为输入，数值研究干涉光刻的刻蚀性能，进而分析相干态振幅和相位对光刻分辨率以及条纹可见度的影响，并根据相关物理现象给出相应地的解释。

2 物理模型与双光子曝光率函数计算

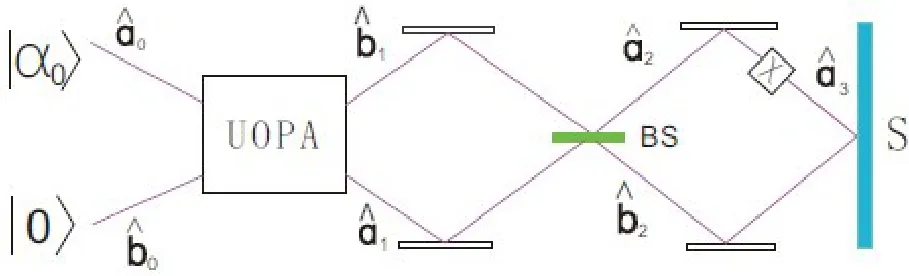
图1 在光学参量放大器中使用相干态和真空态的双光子光刻装置图

其中UOPA代表光学参量放大器，S代表双光子吸收材料。

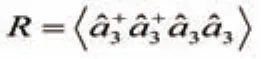
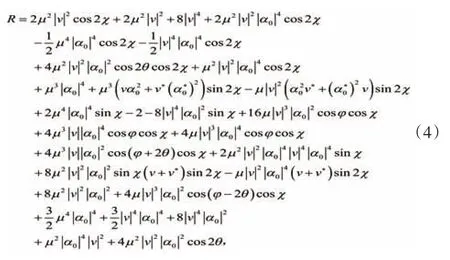
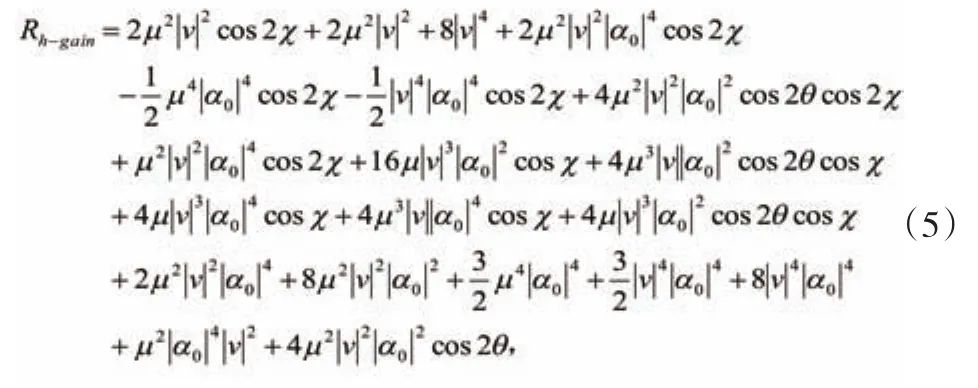
显然，（5）中的前三项与自发参量下转换过程密切相关。

3 数值分析

图2和图3中，通过恰当选择不同增益参量值和相干振幅，我们作出了双光子曝光率函数随经典相移的变化曲线，从图2（a）与图3（a）可看出：当时，曝光率函数周期为2，且相邻的主级亮条纹间存在一个次级亮条纹，且当增大相干振幅时，主极大亮纹强度将会被增强，而次极大条纹强度却依然保持不变；另一方面，随着相干振幅值不断增加，暗条纹强度也将被逐渐增强，最终将超过次极大条纹强度，这时，次极大条纹相应地就转变为暗纹；此外，通过比较图1（b，c）和2（b，c），发现归一化条纹图案极大地依靠激励相干光束强度。

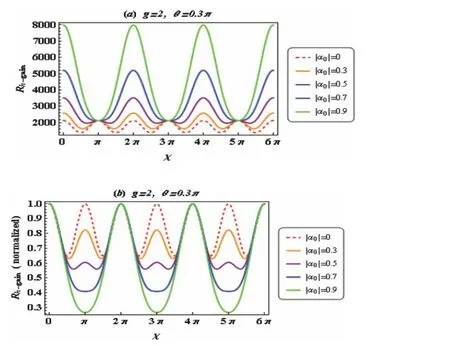
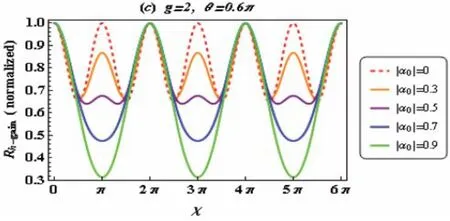
图2 双光子吸收率随经典相移的变化曲线图

图3 双光子吸收率随经典相移的变化曲线图

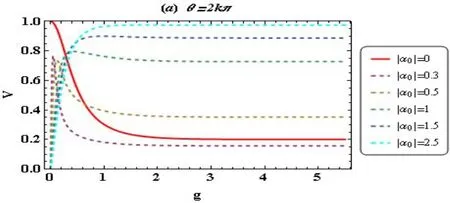
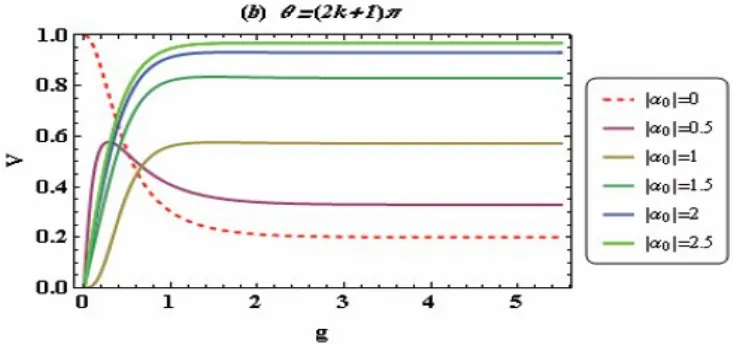
图4 条纹可见度随增益参数的变化曲线图

图5 条纹可见度随相干光束的相位的变化曲线图

4 讨论与结论

综上所述，我们研究了相干光束和真空输入下的高增益参量放大过程中的双光子干涉光刻的行为特性。由于本方案中的输入相干场是经典场，且与另一输入场（真空）是量子不相关的，虽然二者经高增益参量放大器作用后，输出场具有量子相关性，但这种量子相关性将严重受到来自于输入相干光束的经典效应的限制，从而使得本方案所获得的曝光率函数未能有效地打破衍射极限，但方案却能明显地提高条纹可见度。

[1]K.Suzuki，B.W.Smith，Microlithography:Science and Technology [M].2nd Revised Edition，CRC Press Inc，New York，2007.

[2]A.K.Wong，Resolution Enhancement Techniques in Optical Lithography[M].SPIE-International Society for Optical Engineers，Tutorial Texts in Optical Engineering，TT47，2001.

[3]R.F.Pease and S.Y.Chou，Lithography and Other Patterning Techniques for FutureElectronics[J].Proceedings of the IEEE，2008，96: 248-270.

[4]H.Cable，R.Vyas，S.Singh，and J.P.Dowling，An optical parametric oscillator as a high-fluxsource of two-mode light for quantum lithography[J].New J.Phys.，2009，11:113055.

[5]C.Kothe，G.Bjrk，S.Inoue，and M.Bourennane，On the efficiency of quantum lithography[J].New J.Phys.，2011，13:043028.

[6]H.Fujiwara，Y.Kawabe，R.Okamoto，S.Takeuchi，and K.Sasaki，Quantum lithography underimperfect conditions:effects of loss and dephasing on two-photon interference fringes[J].J.Opt.Soc.Am.B，2011，28:422-431.

[7]Y.S.Kim，O.Kwon，S.M.Lee，H.Kim，S.K.Choi，H.S.Park，and Y. H.Kim，Towardsinterferometric quantum lithography:observation of spatial quantum interference of thethree-photon N00N state[J],Proc.of SPIE，2011，8163:816314.

[8]E.A.Sete，K.E.Dorfman，and J.P.Dowling，Phase-controlled entanglement in a quantum-beat laser:application to quantum lithography [J].J.Phys.B:At.Mol.Opt.Phys.，2011，44:225504.

[9]S.Rosen，I.Afek，Y.Israel，O.Ambar，and Y.Silberberg，Sub-Rayleigh Lithography UsingHigh Flux Loss-Resistant Entangled States of Light[J].Phys.Rev.Lett.，2012，109:103602.

[10]S.K.Kim，Aerial image formation of quantum lithography for diffraction limit[J].Curr.Appl.Phys.，2012，12:1566-1574.

[11]E.Pavel，S.Jinga，E.Andronescu，B.S.Vasile，G.Kada，A.Sasahara，N.Tosa，A.Matei，M.Dinescu，A.Dinescu，and O.R.Vasile，2 nm Quantum Optical Lithography[J].Opt.Commun.，2013，291:259-263.

[12]G.P.Miroshnichenko，Quantum lithography on bound-free transitions[J].Eur.Phys.J.D，2013，67:257.

[13]A.N.Boto，P.Kok，D.S.Abrams，S.L.Braunstein，C.P.Williams，and J. P.Dowling，Quantum Interferometric Optical Lithography:Exploiting EntanglementtoBeattheDiffractionLimit[J]，.Phys.Rev.Lett.，2000，85:2733.

[14]G.S.Agarwal，R.W.Boyd，E.M.Nagasako，and S.J.Bentley，Commenton“Quantum Interferometric Optical Lithography:Exploiting Entanglement to Beatthe DiffractionLimit”[J].Phys.Rev.Lett.，2001，86:1389.

[15]F.Sciarrino，C.Vitelli，F.D.Martini，R.Glasser，H.Cable，and J. P.Dowling，Experimentalsub-Rayleigh resolution by an unseeded highgain optical parametric amplifier for quantum lithography[J].Phys.Rev. A，2008，77:012324.

[16]C.C.Gerry，Enhanced generation of twin single-photon states via quantum interference inparametric down-conversion:Application to two-photon quantum photolithography[J].Phys.Rev.A，2003，67:043801.

[17]Y.H.Wang，L.M.Kang，Nonmaximally entangled state quantum Photolithography[J]，J.Opt.B:Quantum Semiclass.Opt.，2003，5:405-408.

[18]Y.X.Gong，Quantum interferometric lithography with pair-coherent states[J].Phys.Rev.A，2013，88:043841.

[19]G.S.Agarwal，K.W.Chan，R.W.Boyd，H.Cable，and J.P.Dowling，Quantum states of lightproduced by a high-gain optical parametric amplifierforuse in quantum lithography[J].J.Opt.Soc.Am.B，2007，24:270-274.