步进炉控温系统鲁棒容错控制设计

胡玲艳

（大连大学信息工程学院，辽宁大连116622）

步进炉控温系统鲁棒容错控制设计

胡玲艳

（大连大学信息工程学院，辽宁大连116622）

步进炉是冶金领域广泛使用的多区段大型热处理设备，炉温在系统运行过程中存在时滞及不确定性，本文基于李雅普诺夫稳定性定理及LMI方法，针对炉温进行鲁棒稳定性分析及容错控制器设计。考虑实际系统中存在的测温传感器各种故障情况，引入多模态故障模型，实现了变增益控制器设计，得到了系统渐进稳定的充分条件。最后根据系统温度模型，借助Matlab的LMI工具箱进行仿真及验证，仿真结果表明所得定理能够保证系统具有鲁棒完整性。

步进炉；时滞；不确定性；鲁棒容错控制；LMI

步进炉热处理过程是一个典型的复杂工业过程控制系统，内部工艺环节多、控制难度大，业内专家、学者也一直持续着对该类炉型设备的先进控制技术研究及应用设计工作，从不同的角度提出新的控制理论及方法，这也为其它复杂工业过程的控制方法研究提供了借鉴和参考。对步进炉控制技术的研究不仅有节能降耗的实际需要，也是对计算机控制技术和智能化综合控制方法的研究与实践［1-2］。

本文以宁夏中色某集团公司所建一座铜扁锭天然气步进式加热炉为研究背景，针对采用时域方法所建立的炉温动态数学模型，考虑系统存在的不确定性和滞后特性，针对系统运行过程中可能存在的传感器故障，进行鲁棒容错控制研究，为该类系统采用鲁棒控制策略进行实际程序设计提供一定参考。

1　系统模型

1.1系统温度分布模型

步进式加热炉主要为铜及铜合金锭进行加热，采用端进、端出步进式结构，从进料端到出料端分为余热回收段、加热段、保温段。由于炉型较大，为提高系统控温的均匀性，加热段、保温段又分为多区段进行控制［3］。炉子内部分区见图1。

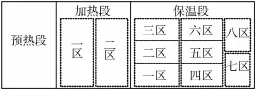
图1　步进炉内部分区示意图

如图1所示，在系统控制过程中，各区温度通过热电偶进行检测。预热段不做控制，只设一支热电偶T0进行温度监控。加热段和保温段是控制段，加热段分为两区，两区单独控制，加热一区设两个热电偶检测点T1和T2；加热二区设两个热电偶测温点T3和T4。在保温段，为保证控温精度及温度分布的均匀性，分区进一步细化，共分为八个控温区，各区分别设一支控温热电偶。图1中虚线所进行的分区，是软件上的虚拟分区，是程序控制上的划分，在满足工艺控制要求的前提下，分区也可采用其它形式［3］。

针对步进炉控制工艺，以加热段一区炉温控制为例，考虑实际系统的状态不确定性与时滞性，给出如下炉温分布状态空间方程：

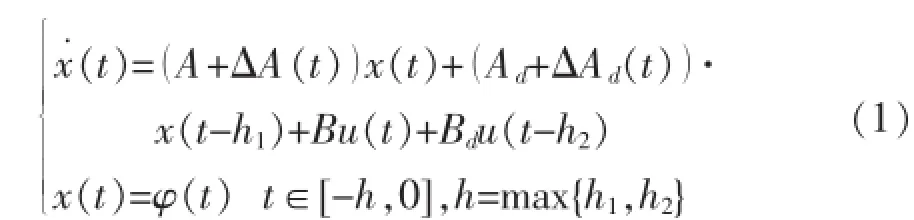
其中，状态变量x∈Rn，控制变量u∈Rm，矩阵A，Ad∈Rn×n，B，Bd∈Rn×m，是根据工艺参数辨识后的常数矩阵，h1，h2为系统为该段运行过程中的状态时滞和控制时滞，ΔA，ΔAd代表系统运行过程中存在的状态不确定性摄动，假设其满足如下条件：

［ΔAΔAd］=DH［E Ed］（2）

其中D、E和Ed分别是具有适当维数的常值矩阵，且H（t）满足条件：

HT（t）H（t）≤I（3）

1.2故障模型

假设：在对温度的检测上，考虑各区在控制过程中，热电偶及温度变送器可能出现故障或失效，这里引入故障矩阵S，S为对角矩阵：

S=diag（S1，S2，…，Sm）0≤Si≤σ，σ≥1（4）

式中：Si代表某控温区第i个传感器运行状态；Si为 1代表热电偶及变送器工作正常，Si为0代表断路故障或无信号，Si小于1代表传感器检测信号小于实际值，Si大于1代表传感器信号被放大，即大于实际值［3-4］，如表1所示。

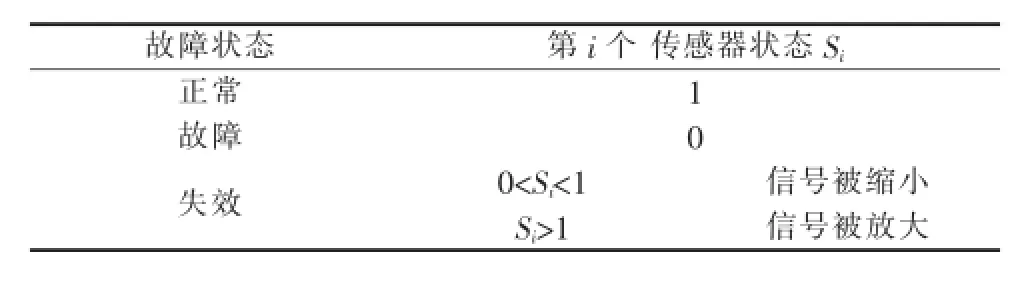
表1　故障模式

2　稳定性分析及控制器设计

针对模型存在的不确定性、时滞性及传感器故障情况，下面推导系统的稳定条件并进行鲁棒控制器设计，在结论推导前首先给出如下引理。

引理1［5-6］:假设X，Y和H是具有适当维数的已知常数矩阵，且满足HTH≤I和α＞0，P∈Rn×n如果P正定，则：

2XTHY≤XTX+YTY（5）

±2XTY≤α-1XTX+αYTY（6）

XTPY+YTPX≤αXTPX+α-1YTPY（7）

XTY+YTX≤αXTX+α-1YTY（8）

引理2［6］（Schur Complement引理）:对于对称矩阵A11，A22和A12，以下条件是等价的：

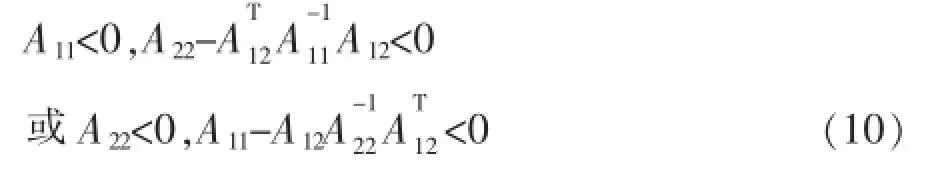
下面针对系统（1）构造变增益状态反馈控制器：

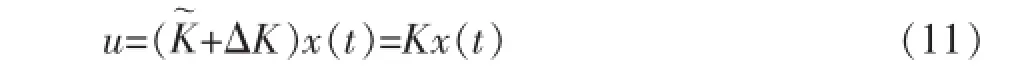
式中：K是反馈增益矩阵；ΔK是增益摄动，这里考虑摄动是由于控制器性能衰减所导致的情况［5］，则

其中δj是不确定参数，满足

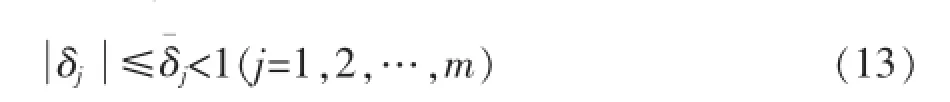
式中δ¯j是常数，在系统调试中采用经验值。将式（11）带入系统（1）中，则闭环系统变为

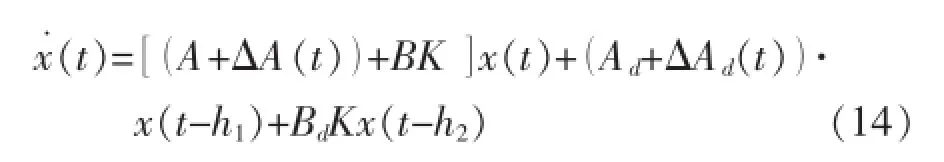
将故障矩阵S引入式（13），则S=diag（s1，s2，…，sm）应放在状态变量x与K之间［7-8］，于是闭环系统模型可写为

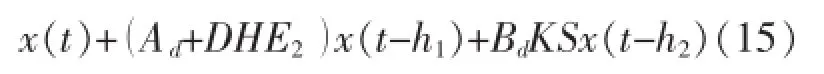
定理：考虑系统（15），对任意可能的传感器故障情况，给定标量αi＞0（i=1，2），如果存在适当维数的矩阵K和对称正定矩阵P＞0，满足如下线性不等式

则系统（11）是鲁棒渐进稳定的，式中“*”表示与上三角矩阵对称，且定义X=P-1，Y=KX，∑=AX+XAT+ BSY+YTSBT。

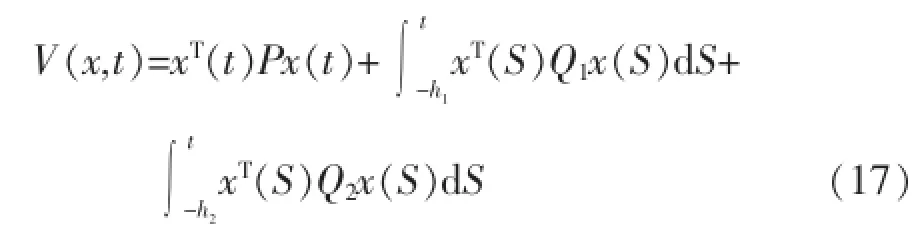
证明：对任意的测温传感器故障，选择如下Lyapunov函数：

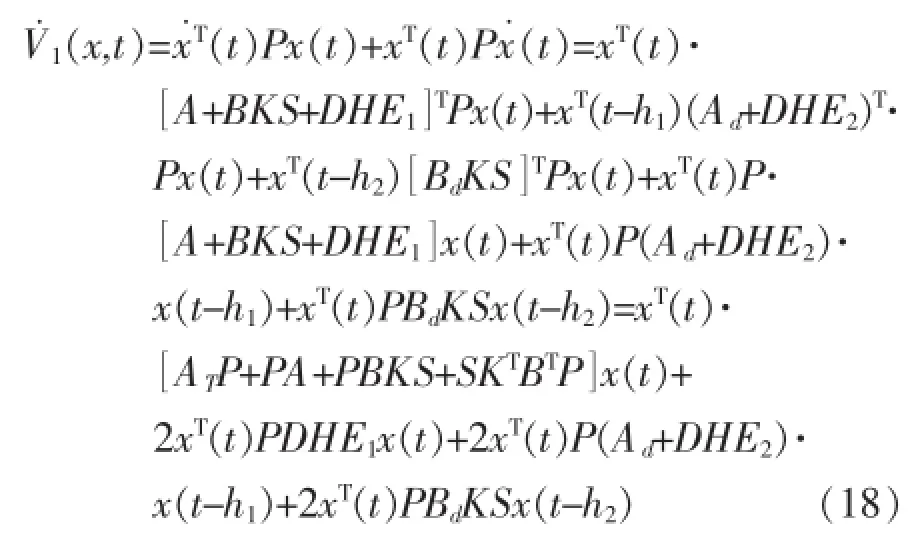
其中定义V1（x，t）=xT（t）Px（t），沿闭环系统（15）计算其导数，可得：

根据引理1，可得

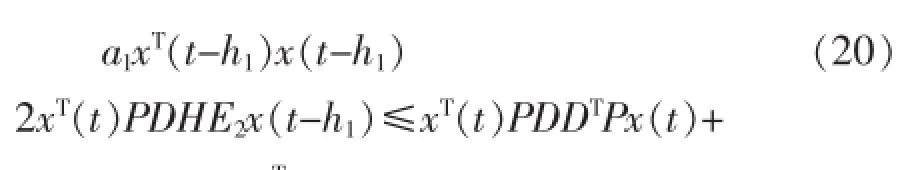
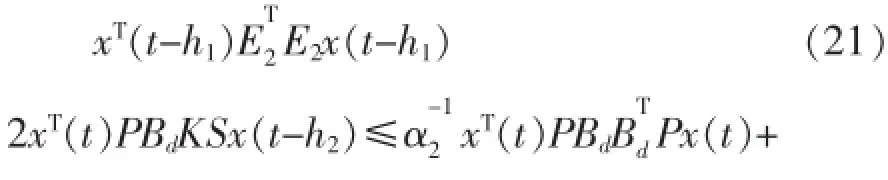
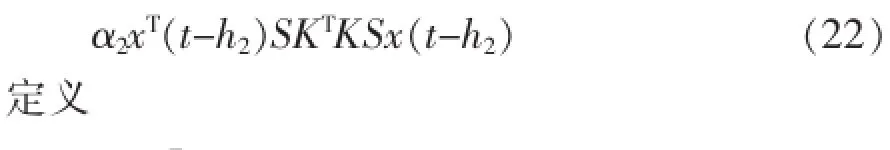
根据式（19）～（24）计算V（x，t）导数，可得：

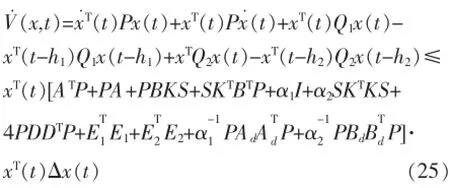
因此

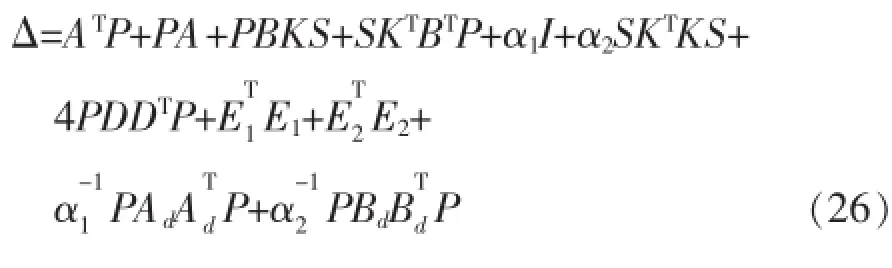
如果Δ＜0，可知V.＜0。根据Lyapunov稳定性定理可知闭环系统（15）是鲁棒渐进稳定的。现对式（25）两边左乘右乘矩阵P-1，并且定义X=P-1，Y=KX，可得：

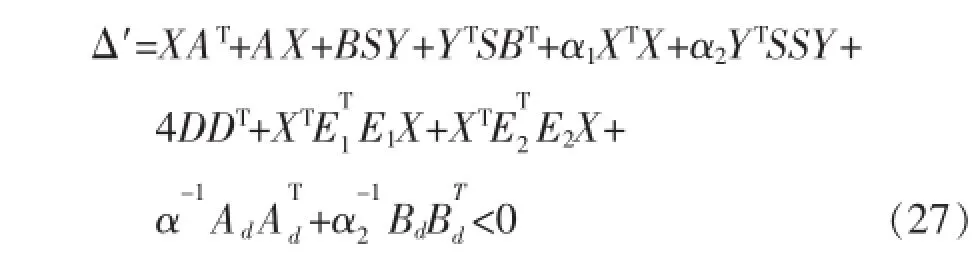
根据引理2（Schur complement），可知式 （27）与式（16）是等价的，证明毕。

3　参数辨识及仿真

定理1推导及证明过程给出了系统稳定的条件及控制器的设计形式，下面以加热段一区为例，考虑如下运行条件：加热段烧嘴功率230 kW，加热一区烧嘴10个，铜坯规格150 mm×330 mm×5 000 mm，材质C17500，步进梁步进速度，坯料进入加热段初始炉温360℃。针对铜锭某批次热处理过程的运行数据采集值，得到无量纲情况下的状态方程基本参数矩阵：

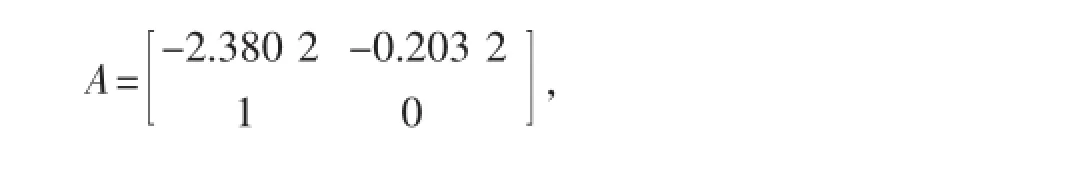
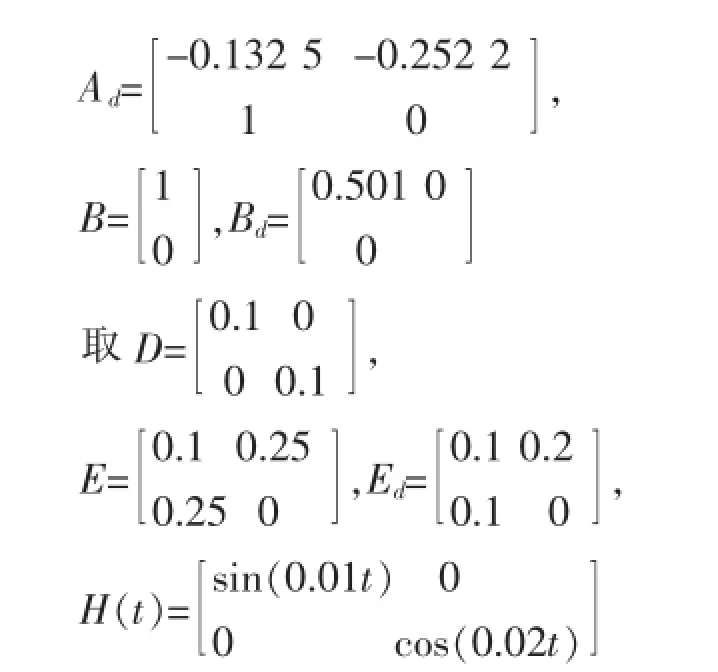
考虑加热一区两个热电偶温度传感器故障状态，设α1=0.2，α2=0.5，h1=0.6Sh2=1.8S时，S0=diag（1，1）代表两个传感器均正常，S1=diag（0，1）代表第一个传感器T0故障，第二个传感器T1正常；S2=diag（1，0）代表第一个传感器T0正常，第二个传感器T1故障；利用Matlab的LMI工具箱，求解由S0，S1和S2构成的线性矩阵不等式，设初始状态x（0）=［5.0；-0.3］T，经仿真，系统的零输入响应如图2所示。

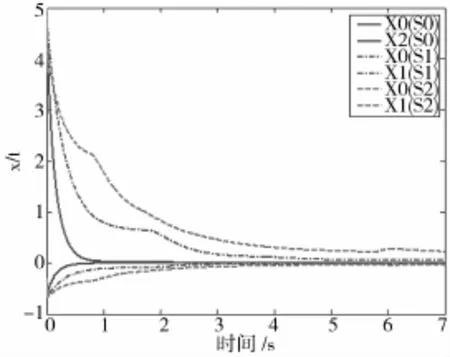
图2　S0，S1，S2故障下系统零输入响应图

当传感器处于失效状态，这里取S3=diag（0.2，1）代表第一测温传感器检测值小于实际值；S4=diag（2.9，1），代表第一个传感器检测信号大于实际值，经过求解由S0，S3，S4构成的线性矩阵不等式组，设初始状态与图2相同，经仿真系统的零输入响应如图3所示。

由仿真曲线可见，系统状态向量X0和X1分别从初始值5.0和-0.3逐渐趋向于零，表明定理1所获得的稳定性条件及容错控制器能够保证系统具有鲁棒完整性。

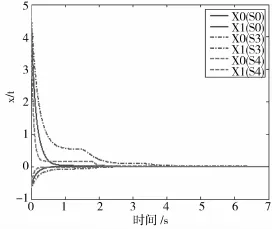
图3　S0，S3，S4故障下系统零输入响应图

4　结语

目前，步进炉控制环节多采用经典PID算法或简化的模糊算法，控制过程中对系统存在的不确定性及时滞性等因素考虑不多。本文考虑系统存在的不确定、时滞性及温度传感器故障情况进行鲁棒容错控制研究，基于李雅普诺夫稳定性定理及LMI方法获得系统稳定条件及控制器结构，对实际生产控制具有较强研究指导意义。

［1］田玉楚，侯春海.连续热镀锌退火炉的数学模型开发［J］.冶金能源，1995，14（3）:38-41.

［2］田玉楚，侯春海.带钢连续热镀锌退火过程的模型化［J］.控制理论与应用，1995，12（4）:459-463.

［3］胡玲艳，王兴城.步进炉控温系统传感器容错控制研究［J］.自动化仪表，2014，35（11）:83-86.

［4］宗臻，王诗宓.基于LMI的输出反馈鲁棒完整性控制器设计［J］.控制理论与应用，2005，22（3）:682-686.

［5］吴敏，何勇.时滞系统鲁棒控制［M］.北京：科学出版社，2009.

［6］陈跃鹏，周祖德.广义系统的鲁棒控制与容错控制［M］.北京：科学出版社，2010.

［7］马喜成，李炜，薛芳.基于时滞状态反馈的鲁棒容错控制［J］.控制工程，2007，14（6）:668-672.

［8］马喜成，李炜.不确定时滞系统的鲁棒容错控制［J］.兰州理工大学学报，2007，33（3）:79-82.

Robust Fault-Tolerant Control Design of Temperature Control System for Beam Reheating Furnace

HU Lingyan
（College of Information Engineering，Dalian University，Dalian 116622，China）

The beam reheating furnace is widely used in metallurgy area as the multi-section largescale heat treatment equipment，and the temperature of the furnace has time-delay and uncertainty features in the process of system operation.Aiming at the temperature，the robust stabilization analysis and the faulttolerant controller were investigated based on the Lyapunov stability theory and Linear Matrix Inequality（LMI）method.Considering all kinds of temperature measuring sensor faults in the actual system，the multimodal failure model was introduced to design of variable gain controller and get sufficient conditions for gradually tends to stabilize.At last，according to the system temperature model and with the help of LMI toolbox of the Matlab，the simulation and validation were used to prove that the theorem can guarantee the system has robust integrity.

beam reheating furnace；time-delay；uncertainty；robust fault-tolerant control；Linear Matrix Inequality（LMI）

TF345.03

B

1001-6988（2016）04-0051-04

2016-04-30

国家自然科学基金自由申请项目60574018，名称：不确定无穷维系统鲁棒控制研究与应用；辽宁省教育厅科学研究项目（LS2013197）

胡玲艳（1978—），女，博士研究生，讲师，主要从事先进智能控制、热处理过程工业控制算法研究设计工作.