基于故障相关性的大型活塞式压缩机压缩系统可靠性分析

裴峻峰 孟朋朋 郭 攀 王 兵 范东亚

(常州大学机械工程学院,江苏 常州 213016)

基于故障相关性的大型活塞式压缩机压缩系统可靠性分析

裴峻峰 孟朋朋 郭 攀 王 兵 范东亚

(常州大学机械工程学院,江苏 常州 213016)

对某大型活塞式压缩机压缩系统进行了可靠性分析。通过对各组件寿命数据的分析得到其寿命分布类型，建立能表达组件之间故障相关性的Copula函数模型，并用AIC准则选出最优Coupla函数模型。运用引入Coupla函数的蒙特卡罗方法对各组件进行抽样，得到系统寿命的抽样值，并运用K-S检测法得到系统寿命分布类型。经验证，运用该方法得到的系统可靠性规律更接近实际。最后，在对压缩系统检修记录统计分析的基础上总结了活塞式压缩机压缩系统主要的故障模式与原因。

可靠性分析 大型活塞式压缩机 压缩系统 故障相关性 Coupla函数 蒙特卡罗方法

大型活塞式压缩机在我国石化行业中应用十分广泛，一般由机体、传动系统、压缩系统、润滑系统、冷却系统、操纵控制系统和附属装置组成，是石化行业中大型复杂设备的典型代表。压缩系统是大型活塞式压缩机最重要的组成部分，包括气阀组件、活塞组件、填料组件和气缸组件[1]。根据某大型炼化企业的维修记录，压缩系统的故障次数约为大型活塞式压缩机总故障次数的66%。国内外现阶段，针对石化大型活塞式压缩机单个部件的故障诊断研究较多，对其各组件和压缩系统寿命规律的研究则较少[2]。因此，准确预测压缩系统寿命，提高大型活塞式压缩机的可靠性，已成为目前亟待解决的问题。

笔者以某炼化企业大型多级活塞式压缩机中的一级压缩系统为例进行了可靠性分析。根据对压缩系统各组件寿命数据的分析，得到各组件可靠性规律。在对压缩系统进行可靠性分析时，引入能描述故障相关性的Copula函数模型，并将它与蒙特卡罗方法结合对系统可靠性进行预测，以避免对各单元进行独立性假设时导致的过大误差[3]，提高压缩系统的可靠性。

1 研究方法①

1.1 威布尔函数与Copula函数

威布尔分布能全面地描述浴盆失效率曲线的各个阶段，是机械设备寿命可靠性分析中使用最广泛的模型之一。当威布尔分布中的参数不同时，它可以蜕化为指数分布、正态分布和瑞利分布。两参数威布尔分布的概率密度函数f(t)及其分布函数F(t)分别为：

其中，t为寿命随机变量；η为尺度参数，在工程领域内也叫特征寿命参数，它给出了分布曲线中点的大致位置；m为形状参数，决定分布曲线的形状。

Copula函数又称为连接函数。由n维Sklar定理可知，若F是随机变量X1,X2,…,Xn的联合分布函数，各随机变量的边缘分布函数为F1,F2,…,Fn，则一定存在一个n维Copula函数C，对于任意x∈Rn，有F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))；若F1,F2，…,Fn是连续的，则函数C是唯一的[4]。此定理表明，任何一个多维随机变量的联合分布函数都可以被分为各随机变量的一维边缘分布和Copula函数两部分。

Copula函数中的阿基米德族函数广泛应用于对多维随机变量联合分布的描述。应用广泛的还有Gumbel Copula函数、Clayton Copula函数与Frank Copula函数。由于Frank Copula函数不适合描述随机变量之间非对称结构的相关关系，而Gumbel Copula函数与Clayton Copula函数广泛适用于处理边缘分布为威布尔分布的情况[5]。因此，笔者选择Gumbel Copula与Clayton Copula函数进行拟合，并选择最优的拟合函数模型，表达式分别为：

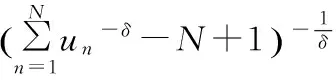
其中，如果un(n=1,2,…,N)为连续的一元边缘分布函数，则un服从[0,1]上的均匀分布[6]。

1.2参数估计

由威布尔分布的概率密度函数得到的寿命时间样本为t1,t2,…,tN的极大似然估计函数为：

lnL(t1,t2,…,tN;m,η)=-m·N·lnη+N·lnm+

(1)

由Copula函数的概率密度函数c(u1,u2,…,un;θ)和边缘密度函数fn(tn;εn)(n=1,2,…,N)，计算得到的联合分布函数的概率密度函数为：

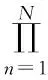
由此概率密度函数得到的寿命时间样本为t1m,t2m,…,tNm(m=1,2,…,M)的极大似然估计函数为：

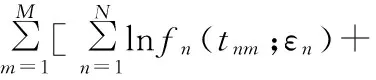
lnc(F1(t1m;ε1),F2(t2m;ε2),…,

FN(tNm;εN);θ)]

(2)

1.3赤池信息量准则

赤池信息量准则(Akaike Information Criterion,AIC)是一种衡量统计模型拟合数据优良性的标准[7]，建立在“熵”的基础上，适用于用极大似然估计法估计参数的情况，其值越小拟合效果越好。具体表达式如下：

AIC=-2lnA+2m

其中，A为模型中极大似然函数值，m为模型中独立参数的个数。

1.4Copula函数的蒙特卡罗方法

当一个系统为串联系统时，可运用引入Copula函数的蒙特卡罗方法对系统的可靠性进行分析。该方法的关键是模拟出具有Copula函数结构的随机变量。笔者以四维Copula函数为例，介绍由4个单元组成的系统的可靠性分析方法。取T1、T2、T3、T4为联合分布函数的4个寿命随机变量，它们的边缘分布函数分别为4个单元的可靠度函数，即U=R1(t1)、V=R2(t2)、W=R3(t3)、X=R4(t4)。由于随机变量U、V、W、X服从[0，1]上的均匀分布，因此，可以从U、V、W、X着手构造随机变量，主要步骤如下：

a. 分别求出Copula函数C(U,V)、C(U,V,W)、C(U,V,W,X)。

b. 在[0，1]区间上模拟出4个相互独立的伪随机数u、b、c、d。

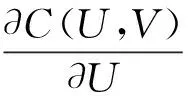
d. 由边缘分布的反函数求得t1=R1-1(u)、t2=R2-1(v)、t3=R3-1(w)、t4=R4-1(x)，此处t1、t2、t3、t4即为有Copula函数结构的寿命随机变量。

2 压缩系统各组件可靠性分析

收集某大型炼化企业2000～2013年25台大型多级活塞式压缩机的失效数据，整理得到一级压缩系统各组件的寿命数据见表1。

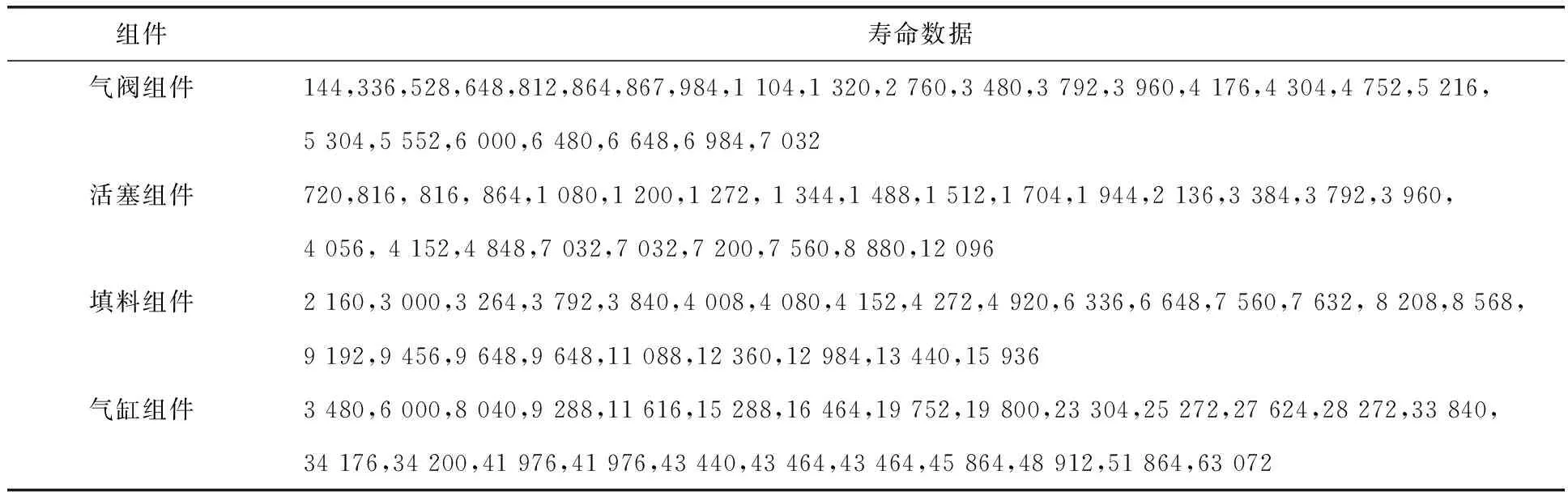
表1 压缩系统各组件寿命数据 h

根据表1中的数据，运用K-S检测法对不同的分布类型进行拟合优度检验。结果表明，压缩系统各组件寿命分布用威布尔分布描述时均通过检测。压缩系统各组件的威布尔分布拟合结果见表2。

表2 各组件威布尔分布拟合结果

可靠度是可靠性分析中最基本的指标，是指在规定条件与时间内完成规定功能的概率。运用极大似然估计法求得威布尔分布各参数，得到各组件的可靠度函数如下：

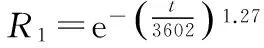
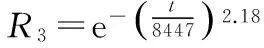
各组件的可靠性曲线如图1所示。可以看出，随着运行时间的增加，气阀组件与活塞组件可靠度下降较快，填料组件次之，气缸组件可靠度下降最慢。

3 压缩系统可靠性分析

大型双作用活塞式压缩机压缩系统的结构示意图如图2所示。

压缩系统的工作过程为：当传动系统带动活塞组件向右运动时，由气阀组件、活塞组件、填料组件和气缸组件组成的右侧密闭空间缩小，压力增大；由气阀组件、活塞组件和气缸组件组成的左侧密闭空间增大，压力下降；气体由阀1进入，阀4排出；同样，当活塞组件向左运动时，右侧的密闭空间增大，压力下降；左侧的密闭空间缩小，压力增大；气体由阀2进入，阀3排出，如此周而复始的工作。由此可知，压缩系统是通过各组件的相互配合进行工作的，任何一个组件发生故障都将导致整个系统无法正常工作。由串联系统的定义可知，系统中只要有一个单元故障，系统就故障[8]。因此，可将大型活塞式压缩机压缩系统当作一个由各组件组成的串联系统。

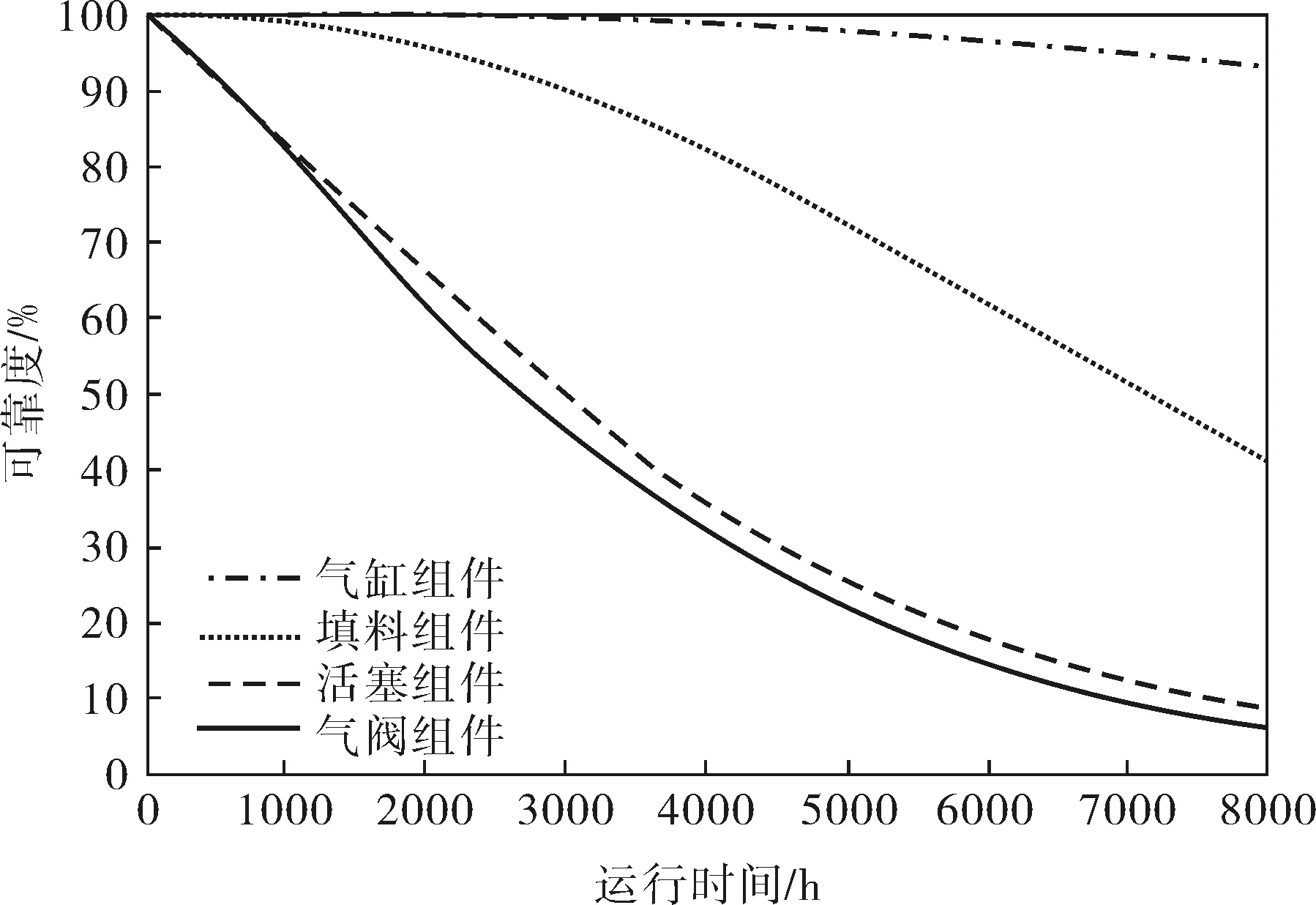
图1 各组件可靠性曲线

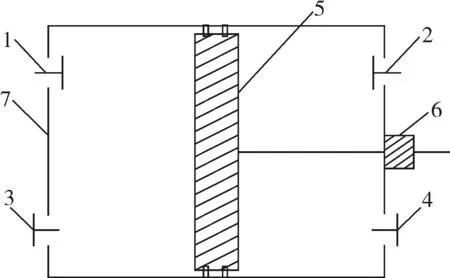
图2 压缩系统的结构示意图

假设各组件之间相互独立，则压缩系统的可靠度R(t)为：

假设各组件之间完全相关，由最薄弱环节理论可知，压缩系统的可靠度为：

R(t)=min(R1,R2,R3,R4)=R1

运用引入Copula函数的蒙特卡罗方法对压缩系统进行可靠性分析，利用极大似然估计法求得Gumbel Copula函数和Clayton Copula函数的参数值与AIC值见表3。

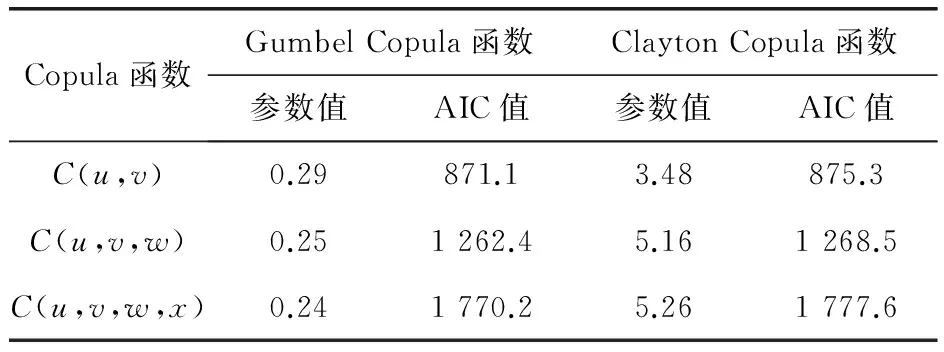
表3 Copula函数参数值和AIC值

由表3可知，3个多维Gumbel Copula函数的AIC值都小于Clayton Copula函数的AIC值。因此，选择Gumbel Copula函数作为系统可靠性的拟合函数。

按照引入Copula函数的蒙特卡罗方法的步骤进行抽样，由串联系统可靠性原则可知，系统寿命为各组件抽样寿命的最小值。重复抽样n次，得到压缩系统寿命的n组抽样值，并对抽样值服从的寿命分布类型进行K-S检测，结果见表4。

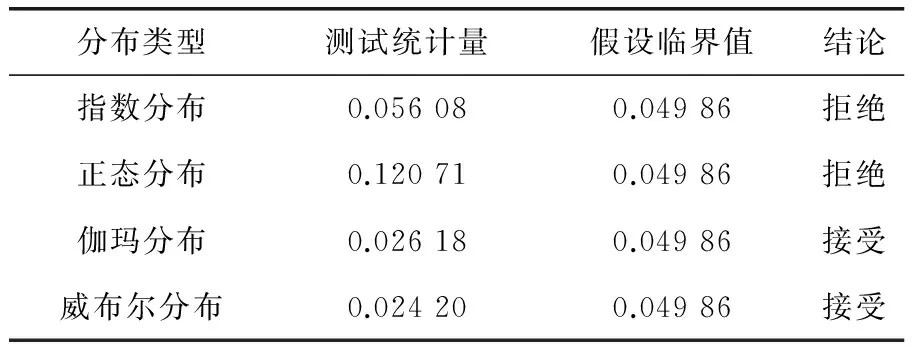
表4 各分布类型的K-S检测结果

由表4可知，压缩系统服从伽玛分布和威布尔分布，但因威布尔分布的测试统计量较小，因此，选择威布尔分布作为压缩系统的可靠性分布模型。分布参数为：尺度参数3 225，形状参数1.23。

运用引入Copula函数的蒙特卡罗方法得到的压缩系统可靠性曲线如图3所示。根据系统可靠度的一般界限理论，由独立假设理论计算得到的是系统可靠度下界值，由最薄弱环节理论计算得到的是系统可靠度上界值[9]。由图3可以看出，运用引入Copula函数的蒙特卡罗方法得到的系统可靠性曲线介于假设组件独立与完全相关系统可靠性曲线之间，说明运用引入Copula函数的蒙特卡罗方法得到的系统可靠性规律更接近实际。

图3 压缩系统可靠性曲线

故障率是可靠性分析中常用的指标，是指工作到某时刻尚未故障的零部件，在该时刻后单位时间内发生故障的概率。则机械设备零部件在t时刻的故障率函数λ(t)为：

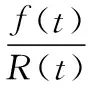
根据引入Copula函数的蒙特卡罗方法得到的威布尔分布参数，绘制出的压缩系统故障概率密度函数曲线如图4所示，故障率曲线如图5所示。

由图4可以看出，压缩系统故障概率密度函数的极值点位于825h左右，即压缩系统在825h左右时故障最多。由图5可知，随着运行时间的增长，压缩系统的故障率不断增加。

4 压缩系统故障模式及其原因分析

在对某炼化企业大型活塞式压缩机检修记录进行分析研究的基础上，得到其压缩系统4个组件的主要故障模式及其原因见表5。

由表5可知，在压缩系统故障模式中，气阀阀片损坏或断裂，气阀弹簧疲劳损坏或断裂，活塞环磨损、断裂或胀死，填料磨损与漏气故障频率最高，其主要故障表现为压缩系统排气压力异常、排气量降低或有明显的摩擦声。因此，在日常维护时要特别注意各仪表的数值变化和缸内异常声音，并对各组件进行定期检修。虽然气缸撞缸或拉缸的故障频率较低，但是一旦发生此类故障，会对气缸组件和活塞组件造成严重的破坏。其主要故障表现为气缸内发出异常响声。因此，在日常维护中要特别注意气缸内有无异常响声，同时，要定期对气缸组件进行检修，并且在检修过程中防止异物进入气缸。活塞杆断裂不仅会损坏活塞体和气缸组件，还会影响企业的安全生产。由于活塞杆断裂大多是没有任何预兆的突然断裂，因此，在日常维护与检修时必须采取定期检查、不定时检测的方式对活塞杆进行跟进管理。

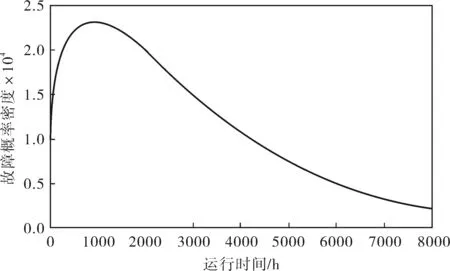
图4 压缩系统故障概率密度函数曲线

图5 压缩系统故障率曲线

组件故障模式故障原因故障频率/%气阀组件阀片损坏或断裂气阀内进入杂物、弹簧严重变形、阀片上结焦或形成积碳42.66弹簧疲劳损坏或断裂介质腐蚀或气阀弹簧本身结构不合理(内部有缺陷)阀座锈蚀或磨损腐蚀性气体与粉尘堆积或密封面偏磨活塞组件活塞体磨损或破裂气缸与活塞的间隙过小或缸内落入异物33.05活塞杆磨损或断裂活塞杆材料问题、加工精度不符合要求或活塞杆跳动量过大活塞环磨损、断裂或胀死吸入气体不清洁、气缸镜面磨损、活塞环开口处的热膨胀间隙不足或活塞环上结焦、积碳填料组件填料磨损填料与活塞杆之间的间隙过小、活塞杆变形或润滑不良21.25填料漏气填料结焦严重、活塞杆磨损不均匀、杆上有擦伤或密封环磨损后收缩不均匀气缸组件气缸撞缸气缸内掉入异物或冷却水大量进入气缸3.04气缸磨损或拉缸缸内积碳严重、吸入气体不清洁(含颗粒杂质多)或活塞环不符合技术要求

5 结论

5.1对某炼化企业大型活塞式压缩机压缩系统中的各组件进行了可靠性分析，得到各组件的可靠性规律。建立了两种Copula函数可靠性模型，通过AIC准则确定 Gumbel Copula函数模型为最优模型，并将它引入蒙特卡罗仿真，得到系统寿命服从尺度参数3 225、形状参数1.23的威布尔分布。将得到的系统可靠性规律与假设组件独立、完全相关可靠性规律进行比较，结果表明，基于故障相关性，运用引入Copula函数的蒙特卡罗方法得到的系统可靠性规律更接近实际。

5.2通过对某炼化企业大型活塞式压缩机检修记录进行分析研究，得到该大型活塞式压缩机压缩系统4个组件的主要故障模式及其原因，提出在日常维护与检修中应特别注意的故障现象和必须采取的检修措施，以保证活塞式压缩机压缩系统安全可靠地工作。

[1] 苗刚.往复活塞式压缩机关键部件的故障诊断方法研究及应用[D].大连:大连理工大学,2006.

[2] Elhaj M,Gu F,Ball A D,et al.Numerical Simulation and Experimental Study of a Two-Stage Reciprocating Compressor for Condition Monitoring[J].Mechanical Systems & Signal Processing,2008,22(2):374～389.

[3] Levitin,Gregory.Incorporating Common-Cause Failures into Nonrepairable Multistate Series-Parallel System Snalysis[J].IEEE Transactions on Reliability,2001,50(4):380～388.

[4] Nelsen R B.An Introduction to Copulas[M].New York:Springer Series in Statistics,2006.

[5] 宋琪.基于故障相关性的加工中心可靠性评价[D].长春:吉林大学,2014.

[6] 张宇.考虑零件失效相关的风电齿轮箱寿命建模[D].兰州:兰州理工大学,2014.

[7] Burnham K P,Anderson D R.Model Selection and Multimodel Inference:A Practical Information-Theoretic Approach [M].New York:Springer,2002.

[8] 金星,洪延姬.系统可靠性评定方法[M].北京:国防工业出版社,2005.

[9] 唐家银,何平,陈崇双.相关性失效机械系统的可靠性分析方法[M].北京:国防工业出版社,2014.

AnalysisofCompressionSystem’sReliabilityofLarge-scalePistonCompressorBasedonFailureCorrelation

PEI Jun-feng, MENG Peng-peng, GUO Pan, WANG Bing, FAN Dong-ya

(SchoolofMechanicalEngineering,ChangzhouUniversity,Changzhou213016,China)

The reliability of a large-scale piston compressor’s compression system was analyzed. Through analyzing the lifespan of its components, their lifespan distribution types were obtained, and Copula function model to express the failure correlation between components was established and its optimal Copula function was selected based on AIC criterion. Through making use of Monte Carlo method which boasting of Coupla function to sample every component, the sample value of the system lifespan was reached, including the distribution type of system lifespan obtained throughK-Sdetection method. The verification results show that, the system reliability based on this method is close to the practical value. Finally, basing on the statistic analysis of the maintenance records, both fault modes and causes of compression system were summarized.

reliability analysis, large-scale piston compressor, compression system, fault correlation,Coupla function, Monte Carlo method

2015-12-20(修改稿)

国家自然科学基金项目(51175051)

TH457

A

1000-3932(2016)07-0712-06