基于EMD奇异值熵和GASVM的转子系统故障诊断方法

毛仲强 王立辉 段礼祥 金 琳 谢骏遥

(1.中国石油塔里木油田分公司，新疆 库尔勒 841000；2.中国石油大学(北京)机械与储运工程学院，北京 102249； 3.天津新港船舶重工有限责任公司，天津 300452)

基于EMD奇异值熵和GASVM的转子系统故障诊断方法

毛仲强1王立辉1段礼祥2金 琳3谢骏遥2

(1.中国石油塔里木油田分公司，新疆 库尔勒 841000；2.中国石油大学(北京)机械与储运工程学院，北京 102249； 3.天津新港船舶重工有限责任公司，天津 300452)

提出一种基于经验模态分解(EMD)和奇异值熵的转子系统故障特征提取方法，克服了奇异值分解相空间重构参数难以选择的问题。然后将奇异值和奇异值熵作为故障特征输入到支持向量机(SVM)中，利用遗传算法(GA)对支持向量机进行参数优化，实现了故障的精确诊断。最后通过对转子不平衡、碰摩和不平衡-碰摩耦合3种故障的正确诊断，证明该方法的有效性。

故障诊断 转子系统 EMD奇异值熵 遗传算法 支持向量机

在石油、化工、电力及航空等行业中，压缩机、离心机及电机等大中型旋转机械起着举足轻重的作用。旋转机械一般由转子系统、轴承及缸体等主要部件组成，其中转子系统是最为关键的部件之一[1，2]。据统计，导致旋转机械失效的原因中，转子故障占50%以上。当转子发生故障时，其振动信号表现出非平稳特性，难以有效提取非平稳信号中的特征进而进行故障诊断，因此研究转子故障诊断具有重要意义[3]。

在转子系统常用的故障诊断方法中，时频域方法能够分析信号的时域或频域信息，但不能同时兼顾信号在时域和频域上的故障特征[4]。随着人工智能技术的发展，大量新技术引入转子系统故障诊断中，其中经验模态分解(Empirical Mode Decomposition, EMD)具有自适应性，能处理非线性和非平稳信号[5，6]。奇异值分解(Singular Value Decomposition, SVD)方法依据良好的数值稳健性，可以在大噪声背景下有效检测突变特征信息，但是由于其特征矩阵构造参数难以选取。奇异值熵在信号信息量评估、信息成分分析等方面有独特的优势，被广泛应用于设备信号处理中[7]。支持向量机(Support Vector Machine, SVM)在处理小样本问题时，具有良好的分类和泛化能力[8，9]，在解决旋转机械故障样本获取问题中具有独特的优势。笔者提出基于EMD分解和奇异值熵的故障特征提取方法，将EMD分解得到的本征模态分量(Intrinsic Mode Function, IMF)组成信号的初始特征矩阵，并求取矩阵的奇异值熵，作为故障特征输入到支持向量机中，利用遗传算法对支持向量机参数寻优，以实现转子系统故障的准确诊断。

1.1 EMD分解方法

EMD分解方法是由美国Huang N E等在研究瞬时频率概念时于1998年提出的，在故障诊断、地震测量等领域有广泛应用[10]。EMD把非平稳信号分解成若干IMF函数，其中频率最低的IMF函数代表着原信号的均值或趋势，其余的IMF函数反映了信号的动态特性，分解步骤如下：

a. 找出信号x(t)的所有局部极大值点和极小值点，分别对它们进行三次样条插值，求出上下包络线。

b. 计算上包络线和下包络线的平均值m1，计算新的数据序列h1，即h1=x(t)-m1。

c. 检验h1是否满足本征模态函数IMF条件，若满足，则h1是x(t)的第一个IMF分量；若不满足，则把h1作为新的信号代入到步骤a、b中重新计算，得到h1的上下包络线均值为m11，则去除包络线均值所代表的低频成分后的数据序列h11=h1-m11。

d. 检验h11是否满足IMF条件，若不满足，则将步骤b、c重复k次，直到h1k满足IMF条件，即h1k=h1(k-1)-m1k。这样得到x(t)的第一个IMF分量，记为c1=h1k，代表着信号x(t)中的最高频率成分。

e. 从x(t)中将c1分离出去，得到剩余序列r1=x(t)-c1。

1.2奇异值熵

信息熵是系统不确定性的定量评价指标，对于系统内在的信息具有较强的刻画能力，其中奇异值熵的应用较为广泛[11，12]。传统的奇异值熵采用Packard等提出的延时嵌陷重构相空间技术，将信号映射到嵌入空间，重构出信号的轨迹矩阵，对矩阵进行奇异值分解求取矩阵的奇异值λi(i=1,2,…,k)，然后计算信号的奇异值熵：

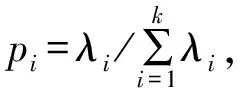
相空间重构技术中关键参数延迟时间和嵌入维数的确定还没有具体的理论指导[13]，现有方法只是确定参数的大概数值。由于信号经EMD分解得到的若干个IMF代表了信号的不同局部特征，且随信号的变化而改变，反映了信号动态特征，因此笔者利用分解得到的IMF分量组成信号的初始向量矩阵A=[c1,c2,…,cn]，代替传统的轨迹矩阵，再按照上述方法计算矩阵的奇异值，得到基于EMD分解的奇异值熵，从而避免了相空间重构中参数选择的问题。

2 SVM

2.1SVM的计算原理

SVM是统计学习理论中最实用的部分，目前仍处于不断发展阶段[14，15]。SVM是一种二类分类模型，其基本思想可用图1的二维空间说明。

图1 SVM线性可分问题

对于线性可分的两类样本，假设数据集合Ω={xi|xi∈Rn,i=1,2,…,l}，xi属于两类中的一类。类用标识yi={-1,1}，则分类方程为：

最优分类超平面是：如果把数据集中与超平面距离最近的点到超平面的距离定义为一类数据与超平面的距离，那么这个距离最大时的超平面就是最优分类超平面，也称最大间隔超平面(如图1中的H)，同时它具有最小的泛化误差。对应这个距离的两个超平面称为分离超平面，经过变换后可以写成wTx+b=±1，对应图1中的H1和H2。从而有：

yi[wTx+b]-1≥0,i=1,2,…,n

此时，分类间隔为2/‖w‖，使得间隔最大等价于‖w‖最小。满足‖w‖最小的分类面称为最优分类面，H1和H2上的训练样本称为支持向量。于是，原问题转化为：

其中l为样本数，用Lagrange乘子法求解：

(1)

求解式(1)即可得到最优分类超平面。当最优分类超平面找到后，只有离最优超平面最近的点有λi>0，成为支持矢量，其他的点都是λi=0，这意味着只有那些离最优超平面最近的点提供最多的分类信息，它们的数量也用来提供超平面的可依赖性的独立界，决策函数可以表示为：

对于非线性不可分模式，可通过核函数K(xi,xj)将样本空间映射到高维特征空间，使其线性可分，并在高维特征空间中构造出最优分类超平面，从而实现分类，如图2所示。

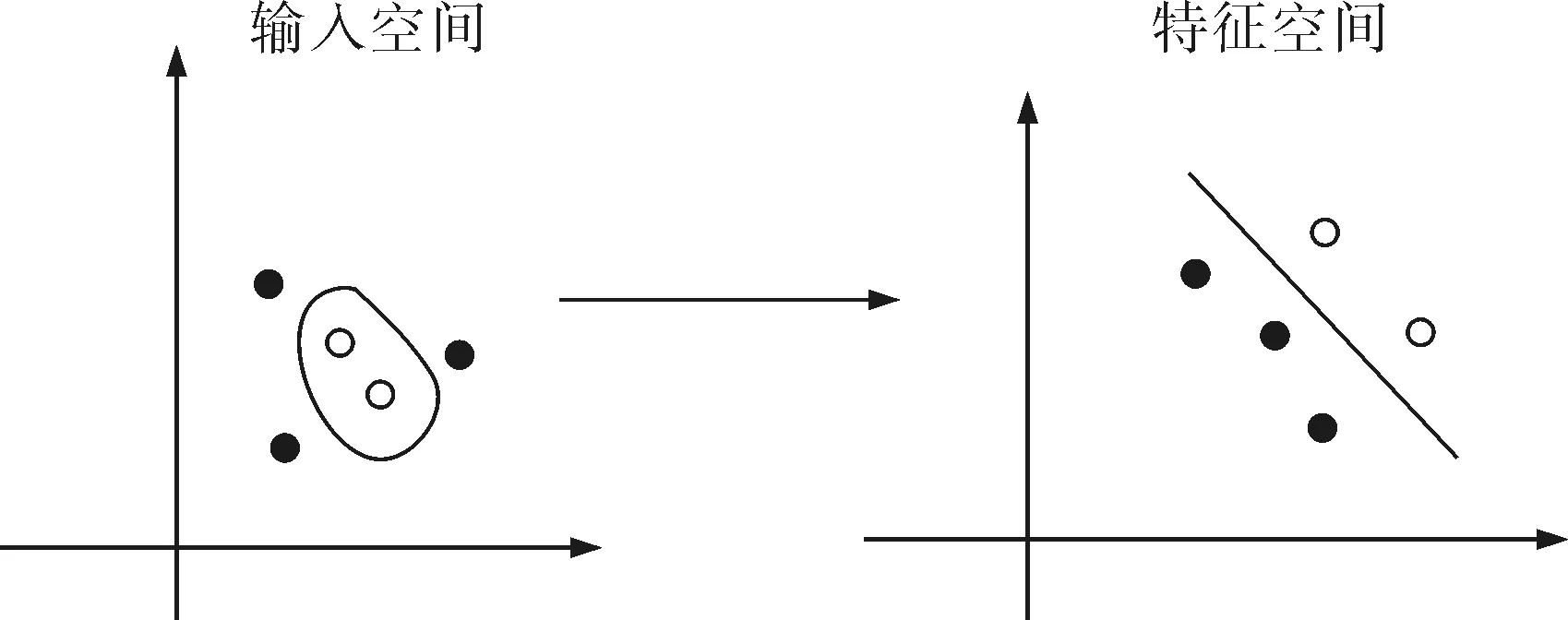
图2 SVM线性不可分问题

引入松弛变量ξi，以及由于松弛变量带来的分类误差而引入的惩罚因子C，则问题转化为：

利用Lagrange乘子法进行求解，最后求得决策函数为：

其中，K(xi,xj)为满足Mercar条件的核函数。

2.2核函数的选择

选择不同的核函数，就得到不同的支持向量，产生不同的SVM算法，目前应用比较多的核函数有3种：多项核函数、径向基核函数和神经网络核函数。由于径向基核函数具有结构简单、参数少等优点，因此笔者也采用径向基核函数，其表达式如下：

3 实例分析

3.1转子故障模拟实验

转子故障模拟实验系统由ZT-3型转子振动实验台、MDES-4数据采集器、传感器和计算机组成，如图3所示。实验转速3 000r/min，采样频率4kHz，分别测取不平衡、碰摩和不平衡-碰摩耦合3种状态的振动信号各100组。实验时，用塑料块与转子圆盘摩擦模拟碰摩故障，添加不平衡块来模拟不平衡故障，加不平衡重和碰摩位置如图3所示。

图3 转子故障模拟实验系统

3.2基于EMD奇异值熵和GASVM的转子故障诊断

以转子碰摩故障采集的一组数据为例，其原始信号和分解信号如图4所示，原始信号被分解为7个IMF分量，其中后3个分量幅值几乎为零，因此这里仅画出前4个IMF分量。

由7个IMF分量构造轨迹矩阵，并计算重构矩阵的奇异值，见表1，前3个IMF分量奇异值之和占7个奇异值总和的92.66%，故选取前3个IMF重构轨迹矩阵，并求取矩阵的奇异值熵，结果如图5所示。可以看出，EMD奇异值熵对于故障类型比较敏感，不同故障类型的奇异值熵不同，不平衡故障状态信号的奇异值熵范围为0.971 9～1.069 1，不平衡-碰摩耦合故障状态信号的奇异值熵范围为0.698 8～0.944 6，碰摩故障状态信号的奇异值熵范围为0.671 0～0.815 2，根据奇异值熵的分布散点图(图5)可以将3种故障基本分开，证实EMD奇异值熵可用于提取转子故障特征。

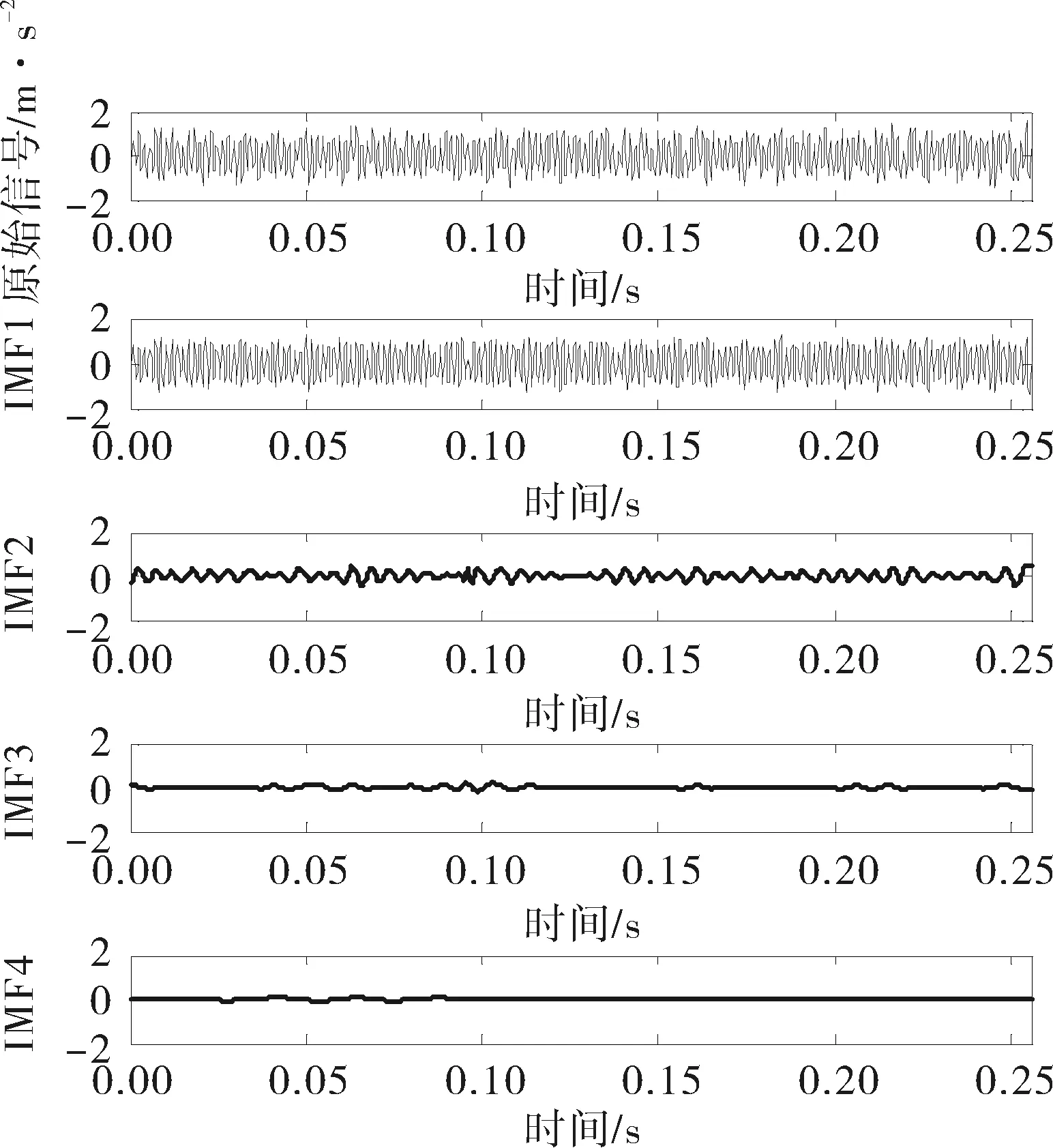
图4 信号EMD分解

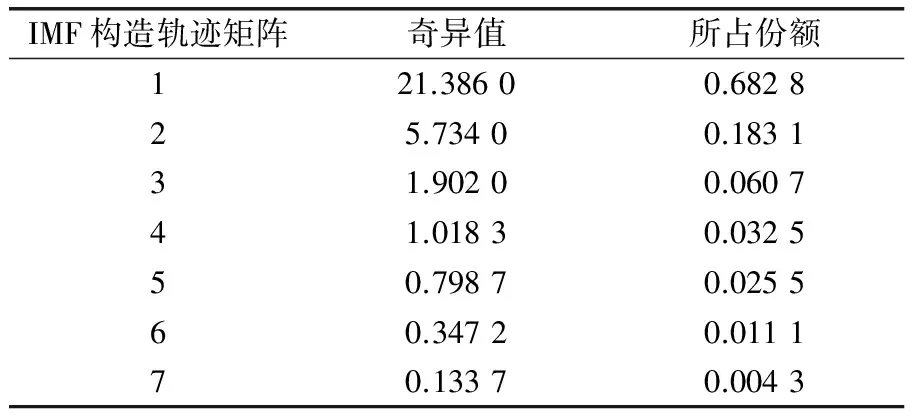
IMF构造轨迹矩阵奇异值所占份额121．38600．682825．73400．183131．90200．060741．01830．032550．79870．025560．34720．011170．13370．0043

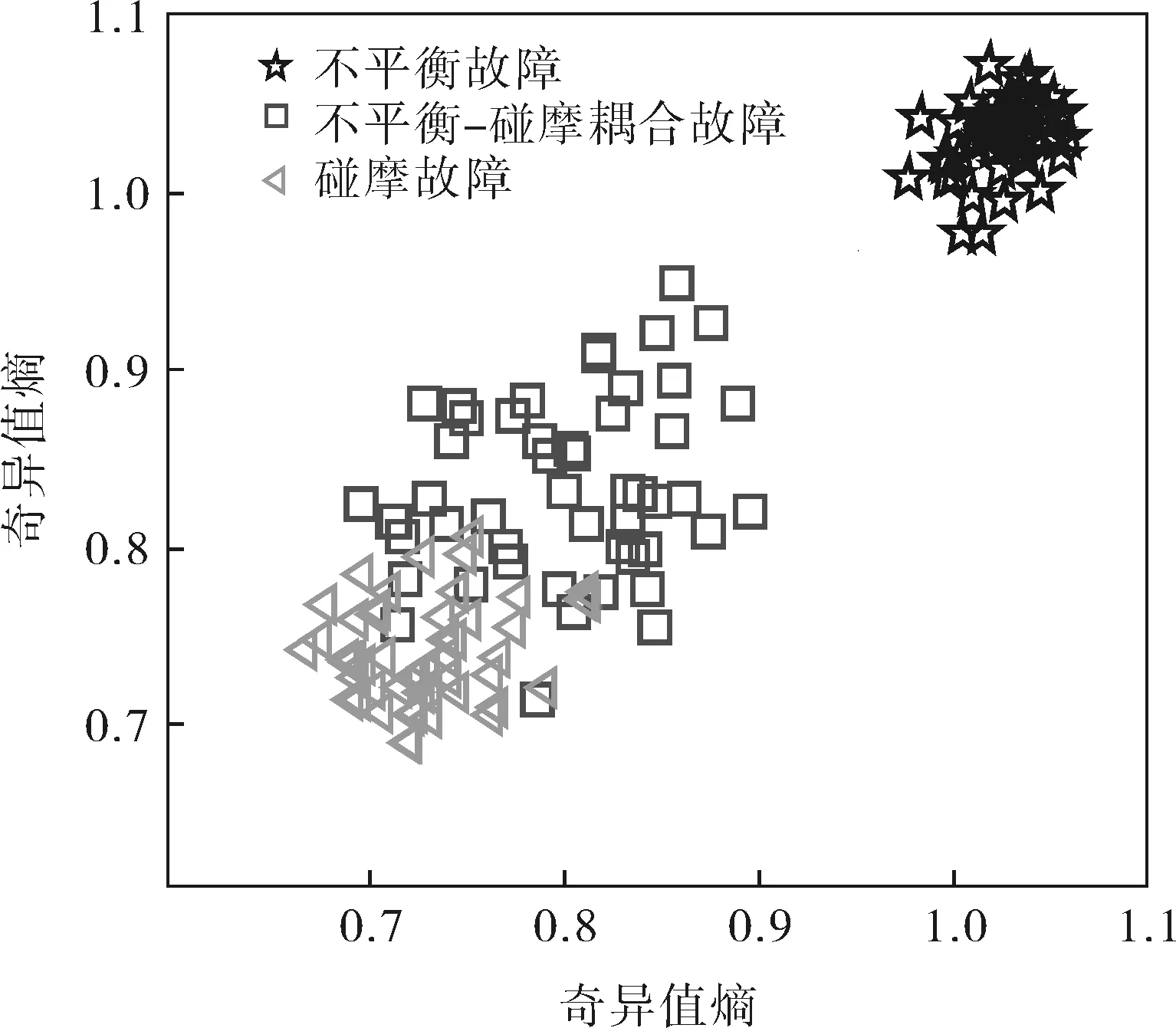
图5 EMD奇异值熵散点图

从图5中可以看出，EMD奇异值熵对于不平衡-碰摩耦合故障与碰摩故障的分类效果不理想。为了更好地识别出转子故障类型，将IMF组成的重构轨迹矩阵的奇异值和奇异值熵一起作为故障特征，输入到SVM中，并将3种故障的前80组作为训练样本，后20组作为验证样本。训练样本见表2(限于篇幅，仅列出5组)。

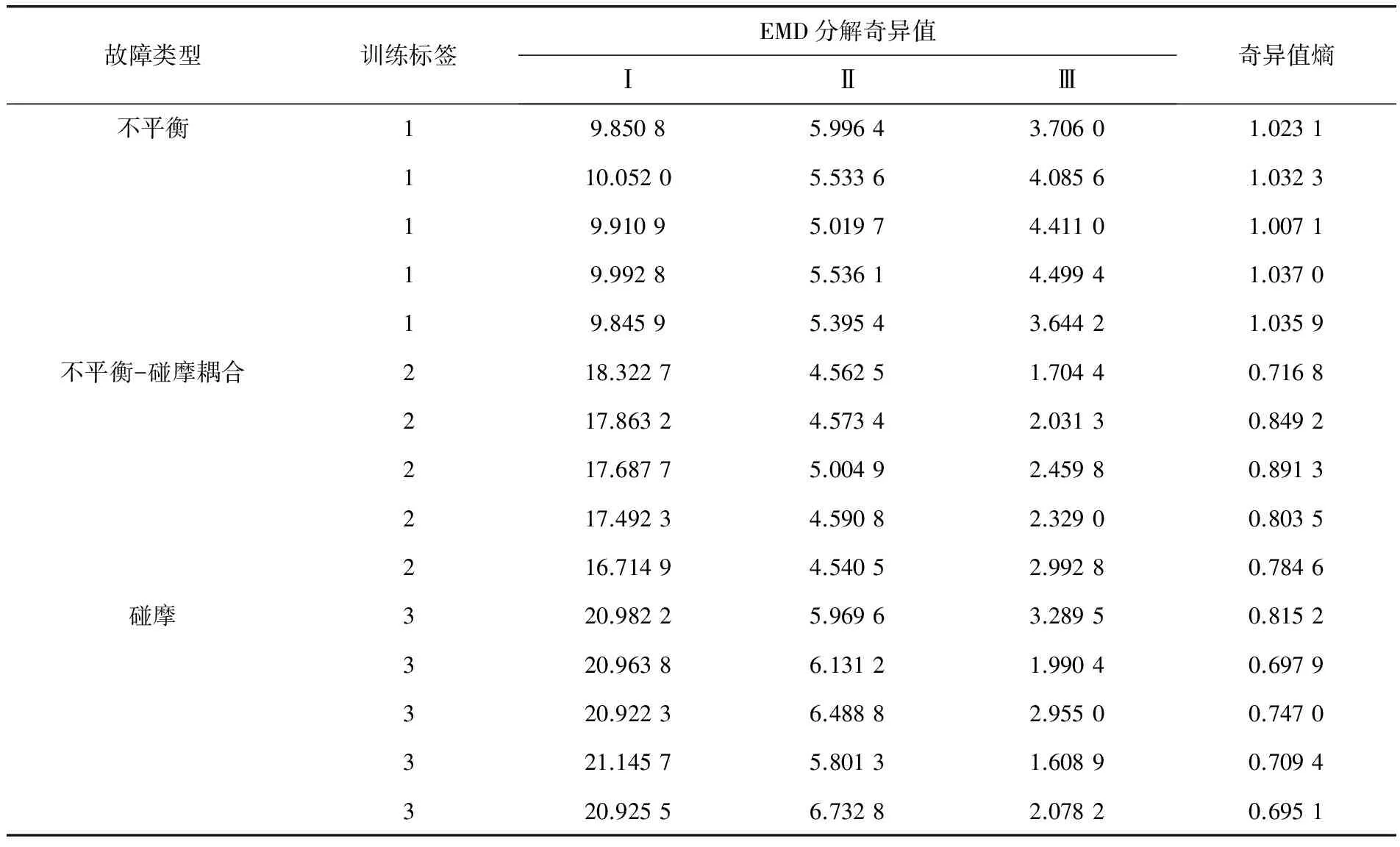
表2 训练样本

进行故障分类时，首先将故障类型进行编号，分别用1、2、3代表不平衡、不平衡-碰摩耦合和碰摩故障。为了提高SVM分类的准确率，引入遗传算法优化支持向量参数(惩罚因子和核函数参数)，将80组样本输入到遗传算法中，得到支持向量机的惩罚因子C=0.037 36，径向基核函数参数σ=0.110 2，然后再构造SVM分类器，并进行训练。最后，将20组验证样本输入到训练好的SVM分类器中，其输出结果和故障类型完全一致，详见表3(限于篇幅，仅列出5组)。证实基于EMD奇异值熵和支持向量机的转子故障诊断方法能够有效提取故障特征和识别转子故障。

表3 验证样本与验证结果

4 结论

4.1利用EMD分解选择3个主要的IMF分量，所组成的初始向量矩阵代替传统的轨迹矩阵，从而解决了重构过程中参数的选择问题。

4.2提出基于EMD和奇异值熵的转子故障特征提取方法，通过对转子不平衡、碰摩和不平衡-碰摩耦合故障信号的分析可知，EMD奇异值熵能够有效地区分出3种故障状态。

4.3为了更好地识别出转子故障，将初始特征向量矩阵的奇异值和奇异值熵共同作为故障特征输入到SVM中，并利用GA算法对SVM的参数寻优，故障分类正确率达到100%，验证了笔者所提方法的有效性。

[1] 郭用坚.旋转机械集中常见故障的分析[J].化工自动化及仪表,1993,20(1):22～26.

[2] 宋军舰,郝点,曹建强.高速转子故障模拟实验研究[J].化工机械,2011,38(4):417～419.

[3] 傅树霞,孙铁,伊辉芹,等.石油化工厂离心泵转子动平衡技术的研究与应用[J].化工机械,2014,41(1):110～113.

[4] 向玲,唐贵基,胡爱军.旋转机械非平稳振动信号的时频域分析比较[J].振动与冲击,2010,29(2):42～45.

[5] Huang N E,Wu M L,Long S R.A Confidence Limit for the Empirical Mode Decomposition and Hilbert Spectral Analysis[J].Proc R Soc Lond A,2003,459:2317～2345.

[6] 周云龙,梁超.基于EMD能量熵的离心泵汽蚀故障诊断研究方法[J].化工自动化及仪表,2010,37(5):41～46.

[7] 张超,陈建军,杨立东,等.奇异值熵和支持向量机的齿轮故障诊断[J].振动、测试与诊断,2011,31(5):600～604.

[8] 陈桂娟,贾春雨,邹龙庆,等.基于腐蚀图像与支持向量机的CO2腐蚀类型识别方法研究[J].化工机械,2014,41(6):742～745.

[9] 宋志强,李著信,张镇.基于SVM的融合算法在管道裂纹缺陷漏磁信号特征识别的应用研究[J].化工自动化及仪表,2011,38(5):536～539.

[10] 武建军,邓松圣,周爱华,等.基于EMD灰色关联降噪的泵机组故障诊断[J].化工机械,2010,37(5):563～566.

[11] 申弢,黄树红,韩守木,等.旋转机械振动信号的信息熵特征[J].机械工程学报,2001,37(6):94～98.

[12] 徐锋,刘云飞.基于EMD-SVD的声发射信号特征提取及分类[J].应用基础与工程科学学报,2014,22(6):1238～1247.

[13] 李晓晨,陈昌雷,赵德阳,等.基于EMD奇异值熵的高压输电线路故障选相新方法[J].中国电力,2011,44(5):6～9.

[14] Cristianini N,Shawe-Taylor J.An Introduction to Support Vector Machines and Other Kernel-based Learning Methods[M].Cambridge,UK:Cambridge University Press,2000:83～108.

[15] 刘鲭洁,陈桂明,刘小方,等.基于遗传算法的SVM参数组合优化[J].计算机应用与软件,2012,29(4):94～96.

RotorSystemFaultDiagnosisBasedonEMDSingularValueEntropyandGASVM

MAO Zhong-qiang1, WANG Li-hui1, DUAN Li-xiang2, JIN Lin3, XIE Jun-yao2

(1.CNPCTarimOilfieldCompany,Korla841000,China; 2.SchoolofMechanicalandTransportationEngineering,ChinaUniversityofPetroleum,Beijing102249,China; 3.TianjinXinggangShipbuildingHeavyIndustryCo.,Ltd.,Tianjin300452,China)

A fault diagnosis approach for rotor system based on empirical mode decomposition (EMD) and singular value entropy methods was proposed, which has the difficulty in selecting phase-space reconstruction parameter in the process of singular value decomposition solved and the singular value and singular value entropy taken as the fault feature to input into the support vector machine (SVM) as well as the genetic algorithm (GA) used to optimize the SVM parameters so as to realize preliminary fault diagnosis. Diagnosing rotor imbalance, rubbing and imbalance-rubbing coupling proves effectiveness of the proposed method.

fault diagnosis, rotor system, EMD singular value entropy, GA, support vector machine

TQ050.7

A

1000-3932(2016)06-0604-06

2016-05-17(修改稿)