基于集成核可预测元分析的非线性故障检测

宋新建 钟 纯 李 楠 杨煜普

(上海交通大学电子信息与电气工程学院，上海 200240)

基于集成核可预测元分析的非线性故障检测

宋新建 钟 纯 李 楠 杨煜普

(上海交通大学电子信息与电气工程学院，上海 200240)

以核可预测元分析(KForeCA)为例，将它与集成学习方法相结合，提出了一种基于集成核可预测元分析(EKForeCA)的非线性故障检测方法。给出EKForeCA的故障检测原理。TE仿真实验结果表明：基于EKForeCA的故障检测方法可有效提高故障检测灵敏度和鲁棒性。

非线性故障检测 核可预测元分析 集成学习方法 统计量

近年来，现代工业过程逐渐趋向于规模化和复杂化，因此工业过程的安全性和可靠性越来越受到人们的关注。随着测量技术的不断发展，工业过程中的大量过程变量被保存下来，为此基于数据驱动的故障检测技术在工业过程中得到了广泛应用[1～3]。

作为一种传统的多元统计故障检测方法，主元分析法(PCA)假设数据服从高斯分布，并且数据变量之间线性相关。然而实际的工业过程数据是有限的，常表现出一定的非高斯性，且不同的工业过程数据具有不同的非线性特征，因此PCA方法在实际应用中存在一定的缺陷[4～6]。核可预测元分析(KForeCA)方法作为一种新兴的数据特征提取方法，考虑了数据之间的时序相关性，能够提取具有动态时序特性和可预测性的数据特征，同时又引入了非线性核函数，能够将低维空间中的数据通过非线性映射投影到高维空间，因此可以很好地处理非线性的过程数据[7，8]。其中，核函数的选择非常关键，这直接影响了该方法提取非线性信息的能力，进而影响故障检测的效果[9，10]。对于核函数的选择，一般的方法是根据经验选择一个核函数并确定核函数的参数，这具有一定的盲目性，很难在故障信息未知的情况下获取合适的核参数，而且即便是对于同一个核函数，不同的故障可能在不同的核参数下具有不同的检测性能[11]。针对该问题，笔者将集成学习方法与KForeCA相结合，提出一种基于集成核可预测元分析(EKForeCA)的非线性故障检测方法，以提高故障检测率，增强过程检测鲁棒性。

1 KForeCA

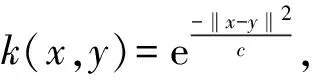
将低维非线性空间的数据映射到线性高维空间后，对高维空间中的数据进行标准化处理。则特征空间F的协方差矩阵ΣF为：

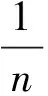
Ki,j=k(xi,xj)=〈Φ(xi),Φ(xj)〉

计算出核矩阵后，对Φ(xi)进行去中心化处理，得到：

(1)

由式(1)可以得出，去中心化后的核矩阵为：

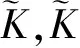
H=[α1,α2,…,αp]

Λ=diag(λ1,λ2,…,λp),λ1≥λ2≥…≥λp

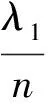
其中，U是经过非线性核映射和白化处理得到的数据，满足E(UUT)=1,U∈Rp。

获得U后，利用ForeCA方法对U进行处理，提取可预测元。ForeCA的基本原理是找到一个线性变换矩阵WT∈Rp×m，使得S=WTU，其中S为得分矩阵，W为负荷矩阵，其列向量为负载向量，且两两正交。W的求取可以转换为求解最优化问题，即：

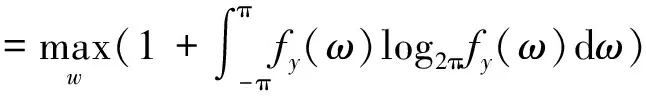
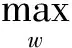
s.t.wTΣUw=1

其中，SU(ω)表示多变量平稳过程的谱密度，ΨU(k)表示自协方差函数，ΣU表示协方差矩阵。

构建KForeCA的过程统计量L2和SPE：

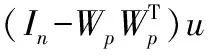
(2)

其中，L2是通过可预测主元模的变化来反映系统趋势变化的统计量；SPE统计量是观测数据到可预测模型空间的距离，反映测量值与可预测模型之间的偏离程度。

2 基于EKForeCA的故障检测

针对KForeCA方法在核函数和核参数选择方面存在的不足，笔者将KForeCA与集成学习方法[13,14]相结合，提出一种基于EKForeCA的故障检测方法。EKForeCA方法选取一系列的高斯核函数进行集成学习，得到多个KForeCA训练子模型，然后利用贝叶斯推理将子模型的检测结果转换成故障概率，通过加权策略突出故障信息，提高故障检测性能。

EKForeCA方法选用的一系列具有不同带宽参数的高斯核函数为：

其中，核函数序号ci=2i-1rmσ2,i=1,…,ns。

然后利用这些核函数分别构造不同的KForeCA子模型，根据式(2)为每一个KForeCA子模型分别构建L2(i)和SPE(i)统计量：

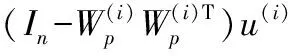
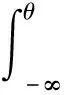
利用贝叶斯推理把每个子模型中已导出的传统检测统计量的数值转换为故障概率，分别为：

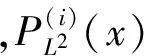
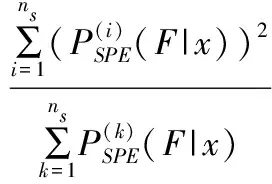
统计量EL2和ESPE的控制限同样可以通过选取合适的置信水平并利用核密度估计方法获得。当两个统计量均未超出各自的控制限时，判定检测过程处于正常状态；当任一统计量超出控制限时，则判定为出现故障，触发故障警报。

3 Tennessee Eastman过程仿真与结果分析

Tennessee Eastman(TE)模型是一个基于实际化工反应过程的基准模型[16]，其过程变量之间具有很强的耦合、非线性及时变等特点，被广泛用于评估过程检测技术。TE过程有41个测量变量(包括22个连续变量和19个成分变量)和12个操作变量。TE仿真模型共预设了21个故障，具体见表1。

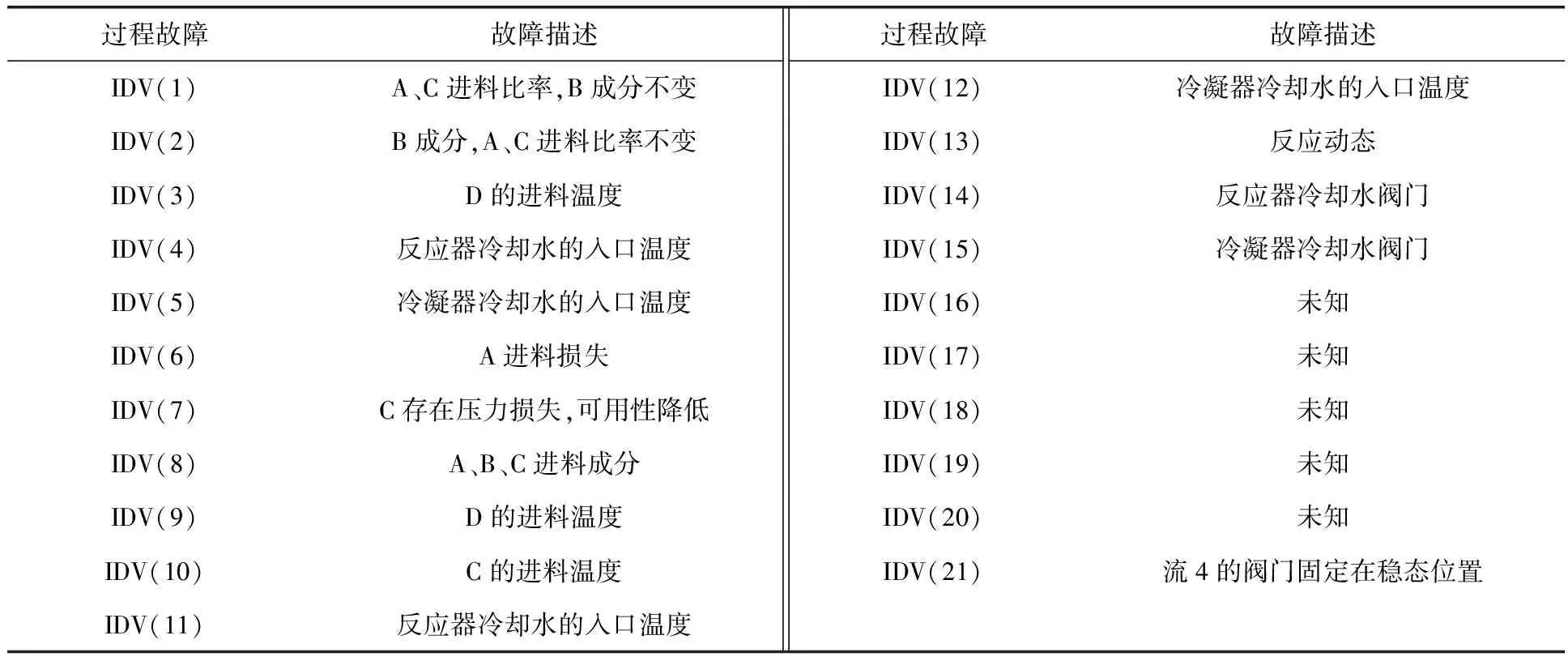
表1 TE仿真模型的过程故障

笔者选取TE仿真模型中的22个连续变量和11个操作变量作为被检测的变量，选取500个运行在正常状态下的数据作为训练数据集，每一个故障测试分别选用960个样本构造测试数据集，且每一个过程故障都是在第161个采样时刻被引入。

高斯核函数的带宽参数通常根据经验公式选择，即c=2i·5m，i=1,2,…,10。TE模型仿真实验分别测试了i=4、i=8时的KForeCA模型与EKForeCA模型对于TE过程21个故障的检测率，结果见表2。其中，L2和EL2分别反映单个KForeCA模型与EKForeCA模型的系统变化趋势，SPE和ESPE分别表示观测数据到可预测模型空间KForeCA与EKForeCA的距离。

表2 KForeCA、EKForeCA模型对21个故障的检测结果

(续表2)

分析表2中的数据可以发现，通过对核函数的集成学习，对于大部分过程故障，EKForeCA基本都能检测出故障的发生与传播，尤其对于故障4、10、11、16、20，其故障检测率得到了显著提升。下面结合故障4和故障16的仿真实验结果进行具体分析。

KForeCA和EKForeCA对故障4的检测结果如图1所示。可以看出，无论是EL2统计量还是ESPE统计量，相比于单个核函数的KForeCA子模型，EKForeCA的检测效果均得到了极大提升。几乎在整个检测周期内，ESPE统计量都能以非常高的灵敏度将故障检测出来。

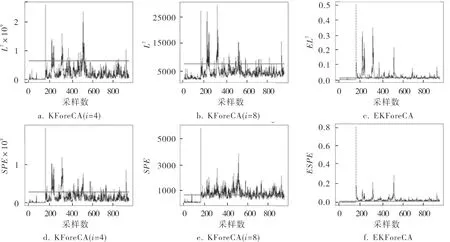
图1 KForeCA和EKForeCA对故障4的检测结果

由表1可知，故障16是一种未知故障，对未知故障的检测效果可以体现出集成核学习方法在故障检测领域中的推广应用能力。KForeCA和EKForeCA对故障16的检测结果如图2所示，可以看出，L2、SPE统计量在采样区间内的检测效果都不是很理想，不同核参数下的检测效果也有很大差异，而基于集成核学习方法的EL2和ESPE统计量基本都能够检测出区间内的绝大部分故障，其检测灵敏度明显优于基于单个核函数的L2和SPE统计量。

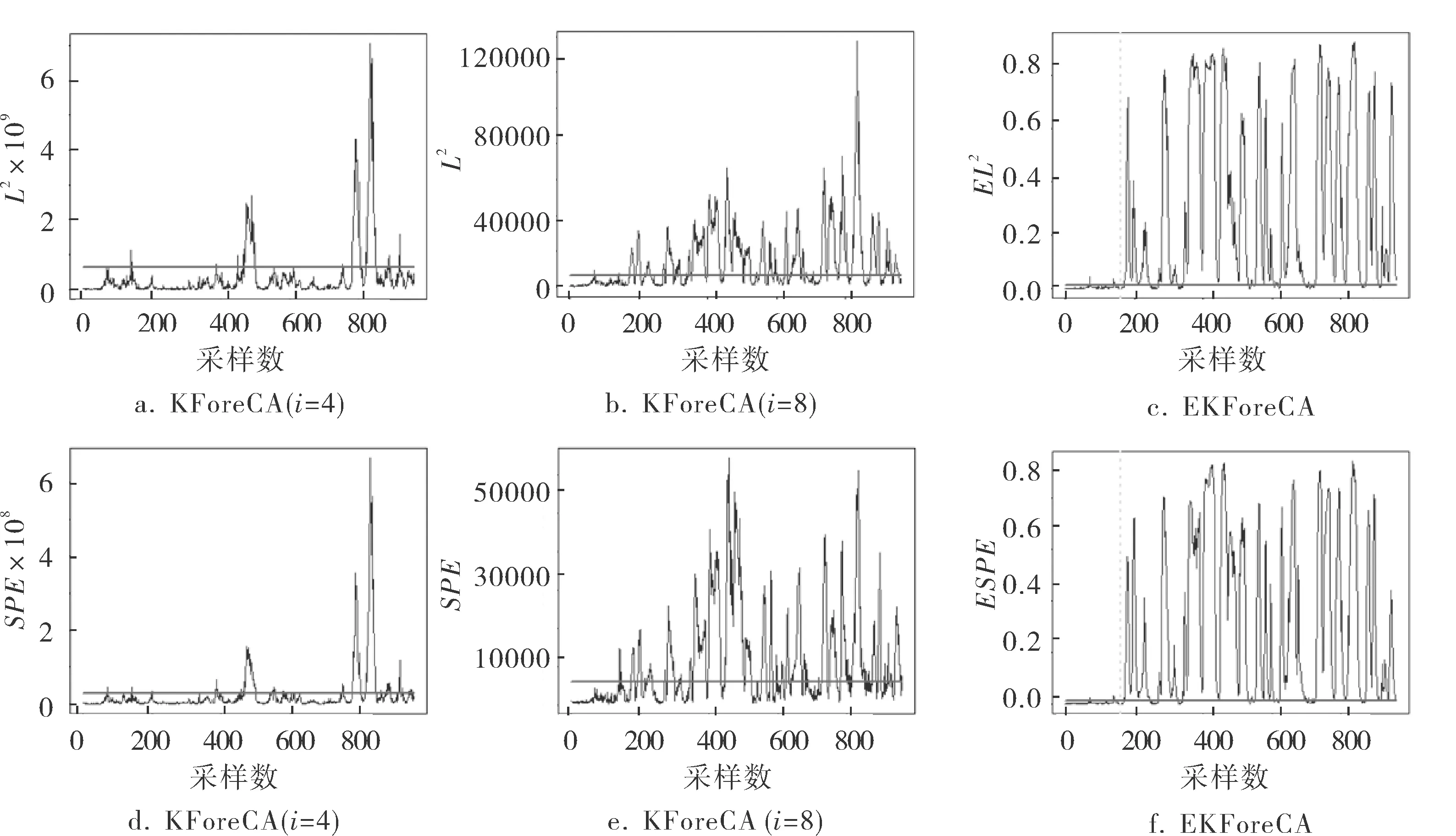
图2 KForeCA和EKForeCA对故障16的检测结果

4 结束语

笔者针对核学习方法中核函数参数选择存在的问题，利用集成学习的思想，以KForeCA为例，将它与集成学习方法相结合，对一系列的核函数进行集成学习，训练得到若干不同的KForeCA子模型，利用贝叶斯推理将各个子模型的检测结果转换成故障概率，并通过加权策略突出故障信息，进而提高过程检测性能。通过对核函数的集成学习，避免了盲目选择单个核函数对检测性能的不利影响，提高了过程检测鲁棒性。TE仿真模型的实验结果表明，与基于单个核函数的KForeCA模型的故障检测方法相比，基于集成核学习的EKForeCA故障检测模型显著提高了过程检测性能。因此，基于集成核学习方法的故障检测方法在非线性过程检测领域具备一定的研究潜力与应用价值。

[1] 李晗,萧德云.基于数据驱动的故障诊断方法综述[J].控制与决策,2011,26(1):1～9.

[2] 周东华,胡艳艳.动态系统的故障诊断技术[J].自动化学报,2009,35(6):748～758.

[3] 赫伟英,裴峻峰.往复机械故障诊断技术进展综述[J].化工机械,2010,37(5):671～674.

[4] Jiang Q,Yan X,Huang B.Performance-Driven Distributed PCA Process Monitoring Based on Fault-Relevant Variable Selection and Bayesian Inference[J].IEEE Transactions on Industrial Electronics,2016,63(1):377～386.

[5] Ge Z,Song Z,Gao F.Review of Recent Research on Data-Based Process Monitoring[J].Industrial & Engineering Chemistry Research,2013,52(10):3543～3562.

[6] 王迎,王新明,赵小强.基于小波去噪与KPCA的TE过程故障检测研究[J].化工机械,2011,38(1):49～53.

[7] Goerg G.Forecastable Component Analysis[C].The 30th International Conference on Machine Learning.Atlanta:ICML, 2013:64～72.

[8] 林圣才,杨煜普,屈卫东.一种基于可预测元分析的故障诊断方法[J].化工自动化及仪表,2015,42(3):272～276.

[9] Lee J M,Yoo C K,Sang W C,et al.Nonlinear Process Monitoring Using Kernel Principal Component Analysis[J].Chemical Engineering Science,2004,59(1):223～234.

[10] Cho J H,Lee J M,Sang W C,et al.Fault Identification for Process Monitoring Using Kernel Principal Component Analysis[J].Chemical Engineering Science,2005,60(1):279～288.

[11] Li N,Yang Y.Ensemble Kernel Principal Component Analysis for Improved Nonlinear Process Monitoring[J]. Industrial & Engineering Chemistry Research,2015,54(1):318～329.

[12] Sang W C,Lee C,Lee J M,et al.Fault Detection and Identification of Nonlinear Processes Based on Kernel PCA[J]. Chemometrics & Intelligent Laboratory Systems,2005,75(1):55～67.

[13] Banfield R E,Hall L O,Bowyer K W,et al.A Comparison of Decision Tree Ensemble Creation Techniques[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2007,29(1):173～180.

[14] Polikar R.Ensemble Based Systems in Decision Making[J].IEEE Circuit Systems Magazine,2006,6(3):21～45.

[15] Chen Q,Kruger U,Meronk M,et al.Synthesis ofT2,andQ,Statistics for Process Monitoring[J].Control Engineering Practice,2004,12(6):745～755.

[16] Downs J J,Vogel E F.A Plant-Wide Industrial Process Control Problem[J].Computers & Chemical Engineering,1993, 17(3):245～255.

NonlinearFaultDetectionBasedonEnsembleKernelForecastableComponentAnalysis

SONG Xin-jian, ZHONG Chun, LI Nan, YANG Yu-pu

(CollegeofElectronicInformationandElectricalEngineering,ShanghaiJiaotongUniversity,Shanghai200240,China)

Taking KForeCA(Ensemble Kernel Forecastable Component Analysis)as an example, having it combined with ensemble learning and KForeCA based to put forward the nonlinear fault detection method was implemented, including the presentation of EKForeCA fault detection principle. The TE simulation results show that, that the EKForeCA-based nonlinear fault detection method can improve the sensitivity of fault detection effectively and the robustness.

nonlinear fault detection, KForeCA, ensemble learning method, statistics

TH165+.3

A

1000-3932(2016)09-0917-06

2016-02-25(修改稿)