基于数据挖掘方法的压缩机二元叶轮优化研究

满超 孙皓 薛米米/重庆通用工业（集团）有限责任公司

基于数据挖掘方法的压缩机二元叶轮优化研究

满超 孙皓 薛米米/重庆通用工业（集团）有限责任公司

0　引言

数据挖掘（Data Mining）［1］是一种高效的数据分析方法，主要特点是可以从大量不完全的、模糊冗杂的数据中，提取其中的潜在有用信息，揭示数据之间的内在联系。数据挖掘方法前期在营销管理方面得到较广泛的应用，为管理者的决策提供有力的支撑，李薇［2］等利用该方法对商品的进销存系统进行了研究。在流体机械方面，国际上已有相关研究，Koji SHIMOYAMA等［3］应用数据挖掘技术对离心扩压器进行了研究；Sugimura K.［4］应用数据挖掘方法对透平机械进行了相关的优化研究。而在国内，相关研究甚少。

数据挖掘方法可以明确各个设计参数对任何一个性能函数的影响大小，同时也可以挖掘出设计参数对每个性能函数的影响规律，可以提供“成片”的优化结果，跟传统的优化方法相比具有明显的优势。

1　数据挖掘方法简介

目前，数据挖掘技术在流体机械相关领域中的应用仍处于探索阶段，其中两种数据挖掘方法被有效地应用于流体机械的设计与优化中。

1.1总变差分析方法

总变差分析方法（Analysis of Variance，ANOVA）采用统计学分析方法［3］，对样本空间中的数据进行分析，可以量化并揭示不同设计变量以及各变量的共同相互作用对性能函数的影响大小。

每一个变量xi（i=1，2，…，n）对函数f（x）的贡献度就是主效应Si，被定义为：

σi（xi）是主效应的函数形式，被定义为：

μi（xi）是函数f（x）在不考虑xi时的平均值：

在总变差的结果中，Si越大，说明当xi变化时，f（x）变化的越剧烈。

1.2自组织映射法

自组织映射方法（Self-Organizing Map，SOM）［5］，将设计空间样本点或Pareto解集作为输入数据，在保留原始数据特征的前提下将高维数据映射到二维空间，通过提取和对比设计变量和性能函数的二维分布趋势，可揭示不同性能函数之间以及设计变量与性能函数之间的内在联系，从而为流动和换热等多学科问题的机理性分析提供方向性指导。

2　研究对象及方法

2.1研究对象与参数选择

本文以某机组离心压缩机二元叶轮为研究对象，应用数据挖掘方法对其设计参数和性能参数之间的内在关系进行深入分析。

如图2所示，选取二元后弯叶轮叶片进口宽度b1、出口宽度b2、进口安装角β1和出口安装角β2作为设计变量［6］，其它设计参数保持不变，表1为每个变量的取值范围。选取质量流量qm、等熵效率ηs和能量头wtot作为性能参数［7］。通过上述的数据挖掘方法来分析和研究几何参数和性能参数之间的关系。

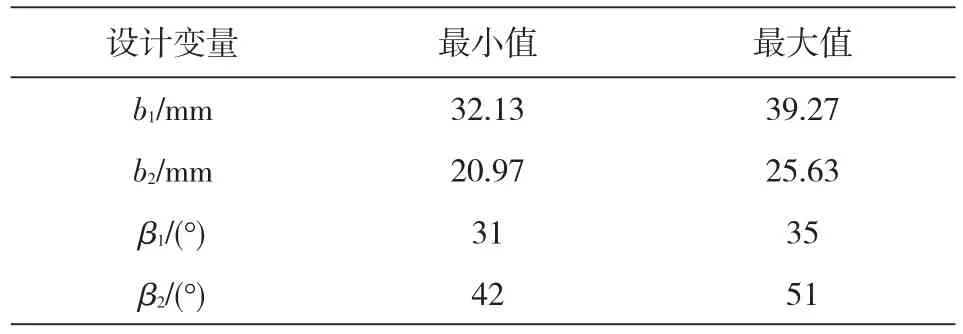
表1　设计变量取值范围

2.2研究流程及方法

本次研究分为数据准备、数值计算和数据挖掘三个阶段，如图3所示。其中数据准备阶段尤为重要，它限定了数据挖掘的对象和范围，直接决定着数据挖掘的意义。首先，是参数的选择［8］。比如，在实际操作中对比发现，将b2替换为b2/b1更为合理，数据挖掘结果更有规律性，这是因为b2/b1反映了轮盖倾角（轮盖斜度）的大小，直接决定了流道的收敛性，并对叶轮的气动性能有着重要的影响［9］。

其次，是设计空间的设计。这一阶段要兼顾样本的数量和分布均匀性。取样的目的是选出有代表性的样本，通过对样本的研究来了解整体。样本数量过多就失去了抽样的意义，并且会大量增加数值计算的时间；数量过少就失去了普遍性，不能确切的反映整体的情况。所以，取样对数据挖掘的结果会有很大的影响，必须采用合适的取样方式。通过拉丁超立方取样（Latin-hypercube sampling）能取出数量合适、分布均匀的样本［10］。它把n个设计变量的空间分为NN个子空间，即每个变量都被分为了相等的N份。然后随机的选出N个样本，其中每个样本都满足正交条件，这样就不会选到重复的子空间，如图4所示。所以，拉丁超立方取样能在样本数量较小的情况下保证样本的分布均匀性。在本次研究中，采用该方法对由四个设计变量组成的设计空间抽取了40个初始样本。

2.3网格及边界条件

为了保证样本之间的可比性，应尽可能降低网格对数值计算结果的影响，即保证设计空间中所有样本的网格、边界条件和计算设置完全一样。本次研究应用CFD软件NUMECA为40个设计样本制定了统一的网格模板，模板的网格数量为57万左右，第一层边界层高度为0.004mm，如图5所示。在数值计算中，控制方程选用了Turbulent Navier-Stokes方程，湍流模型为Spalart Allmaras［11］；流动介质为可压缩氨，叶轮旋转速度为9 600r/min；进口边界条件采用总温总压，压力为477.5 kPa，温度为306.04K；出口边界条件为压力出口，压力为586.47kPa。

3　数据挖掘结果与流场分析

本文给出了二维神经元平面上各设计参数和性能参数的分布情况。一般来说，如果每个参数在神经元平面的分布均表现出了规律性，则说明数据挖掘过程中的二维映射是成功的。反之，如果有少数几个参数在二维平面上的分布没有规律性则说明参数选择有问题，需要调整。如果多数参数对应的神经元平面上的自组织映射无规律，则说明数据挖掘是失败的。从图6来看，每个设计参数和性能参数的映射结果均体现出明显的规律性，说明自组织映射是成功的，可以进行下一步的深入分析。下面本文根据数据挖掘结果分别分析设计参数对能量头、效率和流量的影响。

3.1设计参数对能量头的影响

由图7可知，β2对能量头的影响在所有设计变量中占有主导地位，为进一步分析和研究设计变量与能量头之间的变化规律，基于SOM的映射结果，图8对神经元平面进行了编码，用不同的颜色表明相关参数组合的位置，图9中则通过散点图表明了各设计参数与能量头之间的关系。需要指出的是，为了方便对比，对设计参数和性能参数均进行了归一化处理，所有参数范围为［0，1］。

从图9中可以看出，由于β2基本上决定了能量头的大小，因此与能量头基本成线性变化关系，β2越大，能量头越大。由离心压缩机原理可知，这种变化规律类似于前弯叶轮、径向叶轮和后弯叶轮之间的区别，β2增大时，气流在流道中的转折角增大，叶轮做功过程中更多的机械能转化为气流的能量。从另一个角度来理解，由于转速u2不变，β2增大时c2u增加，因此能量头（与c2uu2成正比）增大。

由于其它设计参数不起主导作用，在设计范围内变化时与性能参数能量头没有呈现出规律性的关系。以b1为例，当b1=0.4时，对应的5个神经元单元的能量头变化范围较大，进一步分析，这五个神经元单元的颜色表明其在神经元平面中的位置刚好是第4行（从下往上，图8），且变化的趋势为神经元单元依次从左往右，能量头增大。对比图6，这种趋势刚好对应着β2增大和能量头增加。从而说明图9中，除β2外，其它3个变量的结果只是β2所决定的能量头变化规律的一种结果，即另一种表现形式而已。

3.2设计参数对效率的影响

图10给出了4个设计参数在相应范围变化时对效率的影响大小，其中b1和b2/b1对效率的影响较大，β1的影响相对较小，而β2则是通过与b1，b2/b1的交互作用对效率产生了十分有限的影响。

图11的结果表明，b1和b2/b1与效率之间类似于一种“线性”关系，即b1增大或b2/b1减小时，叶轮气动效率增加。从流动机理上看，b1增大时，叶轮相对进口速度w1减小，气动损失减小，效率增加。b2/ b1减小时，轮盖斜度增大，子午流道的收敛度增加，有利于减少流动分离损失和二次流损失，从而也有利于效率的提升。至于β1，相对影响要小一些，因此没有呈现出明显的线性关系，但其基本变化趋势表明β1增大时，气动损失减小，实际上主要是影响了叶轮进口处的攻角损失。

3.3设计参数对流量的影响

图12给出了4个设计参数在相应范围变化时对流量的影响大小，其中b1和β2对效率的影响较大，b2/b1也对流量产生了一定的影响。

分析图13中b1和β2的结果可以发现，其变化趋势与图9比较类似，即β2与流量的变化趋势呈线性关系，b1与流量的变化趋势类似于均匀分布。不同之处在于，与图9相比，β2为定值时，流量的变化幅度相对较大（如在β2=0.7附近），说明β2不占主导地位。b1与流量的关系也说明了这一点，即b1值一定时，流量的变化幅度减小，说明其对流量的影响（相对于能量头）增强。

从流动机理上看，β2增大时，叶轮流量系数增大（见离心压缩机原理图3-8）［12］，在相同转速下，叶轮通流能力增强。b1增大时，叶轮相对进口速度w1减小，但叶轮进口面积增加，整体流量会有一定的增加（见离心压缩机原理图3-22）［12］。

4　优化效果对比

通过以上分析，综合考虑各个设计变量对效率、流量、能量头的影响，得到最终的优化结果，原始模型跟优化后模型的设计变量大小如表2所示。采用前期在NUMECA软件中使用的统一模板对原始模型和优化模型分别建模并计算，计算中，出口边界条件采用流量出口，流量大小为16kg/s，其它边界条件与计算40个样本点的边界条件保持不变。对比优化前后效率和压比的大小，如表3所示，效率提升了3.84％，压比提升了1.58％。

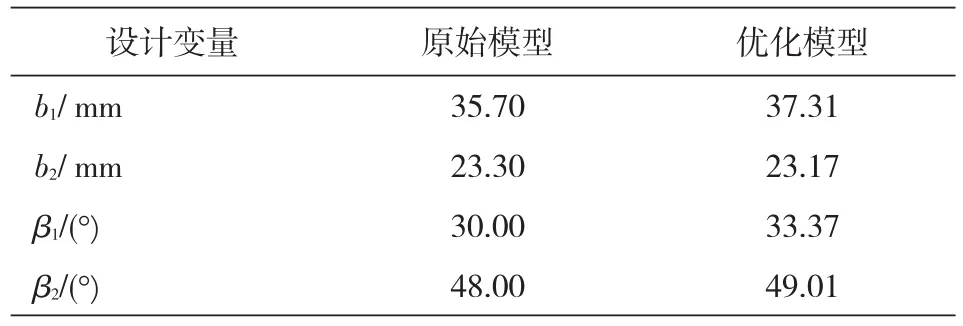
表2　原始模型跟优化后模型设计变量

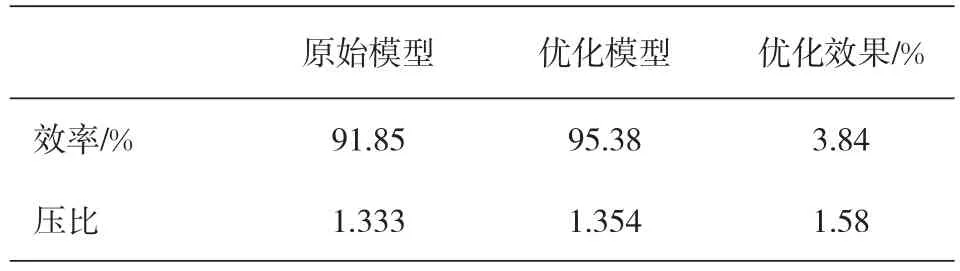
表3　优化前后压比跟效率的对比

4.1速度分布对比

图14为50％叶高处的速度矢量图，从图中可以看出，原始模型中由于叶片进口安装角与气流方向存在一定的夹角，叶片前缘压力面一侧的气流分离现象比较严重，该处气流速度急剧增加，扰乱周围气流的顺畅流动。优化后，叶片进口安装角度有一定程度的增加，使其与气流方向的角度一致，大大减小了此处气流的流动损失。叶片尾缘也有类似现象，适当增加叶片出口安装角后，叶片尾缘处的回流情况明显得到改善，从而减小了叶片尾缘处的流动损失，使二元叶轮的效率得到提升。

4.2熵分布对比

图15为50％叶高处的熵分布云图。通过对叶轮出口高度b2和出口安装角β2进行优化后，在叶片尾缘，气流的回流现象得到明显的改善，从图中可以看出，对比优化前叶片尾缘的熵增，优化后模型的熵增明显的减小，从而从整体上减小气流的流动损失，提升二元叶轮的效率。

6　结论

本文以离心压缩机二元叶轮为研究对象，采用数据挖掘方法对设计空间进行了设计参数和性能参数之间内在关系的深入分析和研究，主要结论如下：

1）数据挖掘方法所揭示的内在规律与离心压缩机基本流动机理相吻合，证明了该方法在揭示设计参数和性能参数之间内在关系的有效性；

2）数据挖掘方法中的总变差分析方法可以帮助设计人员定量地了解设计参数对性能参数的影响大小，有利于设计人员快速地抓住“矛盾的主要方面”；

3）自映射方法揭示了设计参数和性能参数之间的内在关系，设计参数对性能参数的影响越大，其关系越容易呈现出“线性”关系。反之，当影响较小时，由于其分布规律受其它设计参数支配，因此无显著的“线性”关系；

4）对比优化前后的模拟结果，在流量一定的情况下，二元叶轮的效率提升了3.84％，压比提升了1.58％，优化效果明显。

［1］陈文伟.数据挖掘技术［M］.北京：北京工业大学出版社，2002.

［2］李嶶，李宛州.基于数据仓库技术的进销存系统的设计与实现［J］.计算机工程与应用，2001（10）：93-94.

［3］Koji S..Performance Map Construction for a Centrifugal Diffuser with Data Mining Techniques［J］.Journal ofComputational Science and Technology，2010（4）：36-50

［4］Sugimura，K..Design Optimization and Knowledge Mining for Turbo machinery［D］.Tohoku University，Sendai，2009.

［5］毛国君.数据挖掘原理与算法［M］.北京：清华大学出版社，2005.

［6］吴让利，吴沛佳，秦国良.叶片型线对离心风机性能的研究［J］.风机技术，2014（1）：31-36

［7］苏赫，易小兰，张华良，等.某13级轴流压气机加零级气动优化设计［J］.风机技术，2015（1）：33-37.

［8］龚兴龙，陆伟，陆峰.新模型系列风机的快速优化设计［J］.风机技术，2015（2）：48-53.

［9］孟岩，孟继刚，刘洋.离心式压缩机T型叶轮参数化设计程序开发［J］.风机技术，2012（5）：35-38.

［10］程航，闻苏平，徐梓轩，等.小流量系数离心式压缩机叶轮的优化设计［J］.风机技术，2013（3）：43-46.

［11］赵会晶，王志恒，孙晔晨，等.湍流模型对高压比离心压缩机气动性能及流场结构影响的数值模拟研究［J］.风机技术，2014（3）：13-21.

［12］徐忠.离心式压缩机原理［M］.机械工业出版社，2008.

■以离心压缩机后弯叶轮叶片进口宽度、出口宽度、进口安装角和出口安装角作为设计变量；质量流量、等熵效率和能量头作为性能参数。通过拉丁抽样选取40个样本点，分别在NUMECA软件中计算。采用数据挖掘的方法对计算结果进行分析，得到设计变量对性能参数的影响关系，并确定最优设计参数。结果显示，在流量一定的情况下，对比原始模型及优化模型，二元叶轮的等熵效率提升3.84％，压比提高1.58％。

■离心压缩机；数值模拟；数据挖掘；优化；二元叶轮

Optim ization Study of Centrifugal Compressor2D Im peller Based on Data Mining Method

Man Chao，Sun Hao，Xue Mi-mi/Chongqing General Industry（Group）Co.Ltd

The inletwidth，outletwidth，inlet established angle and outlet established angle of centrifugal compressor with backward-bladed impeller were set as design variables.And the mass flow，isentropic efficiency and energy head were set as performance parameters.40 simples were chosen using Latin-hypercube sampling and then simulated in the NUMECA software.After the computational resultsbased on datamining method，the influence of design variables to performance parameters was obtained and got the optimized design variable of 2D impeller. The result shows that，compared the initial model and the optimized modelwith the same mass flow，the efficiency improves 3.84％and thepressureratioimproves1.58％.

centrifugal compressor；numerical simulation；datamining；optimize；2D impeller

TH452；TK05

A

1006-8155（2016）03-0052-07

10.16492/j.fjjs.2016.03.0108

2015-12-25四川重庆