5阶变系数Korteweg-de Vries方程的光孤子解
袁萍, 邓畏平
(1.长江大学文理学院基础课部, 湖北荆州434020;西南财经大学天府学院数学教学中心, 四川绵阳621000)
5阶变系数Korteweg-de Vries方程的光孤子解
袁萍1, 邓畏平2
(1.长江大学文理学院基础课部, 湖北荆州434020;西南财经大学天府学院数学教学中心, 四川绵阳621000)
KDV方程可用于描述量子力学、非线性光学、江河等领域中的非均匀传输介质孤立子的传播,是最典型的非线性色散波动方程的代表。以5阶变系数KDV方程为研究对象,首先结合齐次平衡原理,采用拟设函数法证明了方程当系数满足一定约束条件时存在sech函数形式的亮孤子解与tanh函数形式的暗孤子解;然后在所得孤子解中结合参数的实际背景,选取了一些特殊参数和方程系数进行了数值模拟,刻画了波函数的实际传播形态。与已有的结果进行比较,发现用此方法更加简洁,研究结果完善了KDV方程解的形式,该方法也适用于解决其他非线性波动方程。
光孤子解;齐次平衡原理;变系数Korteweg-de Vries方程;波形图
引言
越来越多有关非线性问题的非线性微分方程已经出现在许多领域,如物理、化学、生物、机械和光学等。例如描述等离子物理中不稳定漂移波的KdV-Burgers-Kuramoto方程[1]、描述短脉冲在单模光纤中传播的非线性Schrödinger方程[2]、描述单种群优势基因传播的Fisher方程[3]等,因此非线性发展方程精确解的研究已经成为一项重要工作。目前,对寻找非线性发展方程的精确解,已经形成较为完善的求解方法,如齐次平衡法[4-5]、首次积分法[6-7]、各种函数展开法和试探函数法[8-9]、逆散射方法[10]、Backlund变换法[11]等。
KDV方程可用于描述量子力学、非线性光学、江河等领域中的非均匀传输介质孤立子的传播,以5阶时变系数KDV方程为研究对象,其形式为:
ut+f(t)u2ux+g(t)uxuxx+h(t)uuxxx+
k(t)uxxxxx=0
(1)
其中:u(x,t)为波函数,f(t),g(t),h(t),k(t)为实解析函数。文献[12]已经推出该方程的Lax对、Darboux变换和一系列解析解,文献[13]利用AKNS变换,构造了方程ut+f(t)u2ux+g(t)uxuxx+h(t)uuxxx+k(t)uxxxxx+l(t)u=0的自Backlund变换和一系列孤子解。
本文利用孤波拟设函数法[14-15]证明当方程(1)的系数满足一定约束条件时,方程存在暗孤子解和亮孤子解,这种方法已经成功运用于若干类非线性偏微分方程[16-18]。
1 变系数KDV方程的亮孤子解
假设方程(1)的解具有如下形式:
u(x,t)=λ(t)sechpξ,ξ=l(t)x+v(t)t
(2)
其中:λ(t)为孤波的振幅,l(t)为逆宽,v(t)为波速,这些函数均待定,p由齐次平衡原理确定。由p+5=2p+3得p=2。
易得:
ut=λ′sech2ξ-2λsech2ξ·tanhξ·
(l′x+v′t+v)
(3)
ux=-2λlsech2ξ·tanhξ
(4)
u2ux=-2λ3lsech6ξ·tanhξ
(5)
uxuxx=4λ2l3(-2sech4ξ·tanhξ+3sech6ξ·tanhξ)
(6)
uxxx=-2λl3(4sech2ξ·tanhξ-12sech4ξ·tanhξ)
(7)
uxxxxx=-2λl5(16sech2ξ·tanhξ-240sech4ξ·
tanhξ+360sech6ξ·tanhξ)
(8)
将(3)式~(8)式代入方程(1)得:
λ′sech2ξ-2λsech2ξ·tanhξ·(l′x+v′t+v)v-
2f(t)λ3lsech6ξ·tanhξ+4g(t)λ2l3(-2sech4ξ·
tanhξ+3sech6ξ·tanhξ)-2h(t)λ2l3(4sech2ξ·
tanhξ-12sech4ξ·tanhξ)-
2k(t)λl5(16sech2ξ·tanhξ-
240sech4ξ·tanhξ+360sech6ξ·tanhξ)=0
(9)
令(9)式中sechiξ·tanhjξ的系数全为0得:
sech2ξ: λ′=0
sech2ξ·tanhξ:l′x+v′t+v+16l5k(t)=0
sech4ξ·tanhξ:λg(t)+λh(t)-60l2k(t)=0
sech6ξ·tanhξ:λ2f(t)-6λl2g(t)-12λl2h(t)+
360l4k(t)=0
(10)
解代数方程组(10)得:
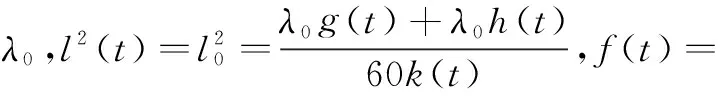
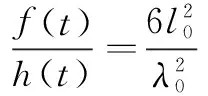
(11)
2 变系数KDV方程的暗孤子解
假设方程(1)的解具有如下形式:
u(x,t)=λ(t)sechpξ,ξ=l(t)x+v(t)t
(12)
其中,λ(t)为孤波的振幅,l(t)为逆宽,v(t)为波速,这些函数均待定。p由齐次平衡原理确定。由p+5=2p+3得p=2。
易得:
ut=λ′tanh2ξ+2λ(tanhξ-tanh3ξ)·
(l′x+v′t+v)
(13)
ux=2λl(tanhξ-tanh3ξ)
(14)
u2ux=2λ3l(tanh5ξ-tanh7ξ)
(15)
uxuxx=4λ2l3(tanhξ-5tanh3ξ+
7tanh5ξ-3tanh7ξ)
(16)
uxxx=2λ2l3(-8tanh3ξ+20tanh5ξ-12tanh7ξ)
(17)
uxxxxx=2λl5(136tanhξ-616tanh3ξ+
840tanh5ξ-360tanh7ξ)
(18)
将(12)式~(17)式代入方程(1)得:
λ′tanh2ξ+2λ(tanhξ-tanh3ξ)·(l′x+v′t+v)+
2f(t)λ3l(tanh5ξ-tanh7ξ)+
4g(t)λ2l3(tanhξ-5tanh3ξ+7tanh5ξ-3tanh7ξ)+
2h(t)λ2l3(-8tanh3ξ+
20tanh5ξ-12tanh7ξ)+
2k(t)λl5(136tanhξ-616tanh3ξ+
840tanh5ξ-360tanh7ξ)=0
(19)
令式(19)中tanhiξ的系数全为0得:
tanh2ξ: λ′=0
tanhξ:l′x+v′t+v+2λl3g(t)+136l5k(t)=0
tanh3ξ:l′x+v′t+v+10λl3g(t)+8λl3h(t)+
616l5k(t)=0
tanh5ξ:λ2f(t)+14λl2g(t)+20λl2h(t)+
840l4k(t)=0
tanh7ξ:λ2f(t)+6λl2g(t)+12λl2h(t)+
360l4k(t)=0
(20)
解代数方程组(20)得:
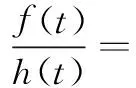
u(x,t) = λ0tanh2
(21)
为刻画孤子解对应的波函数实际传播形态,在(11)式和(21)式中结合参数的实际背景,选取了一些特殊参数和系数进行了数值模拟,图1 、图2 分别模拟了(11)式和(21)式形式的孤子解的波形图。
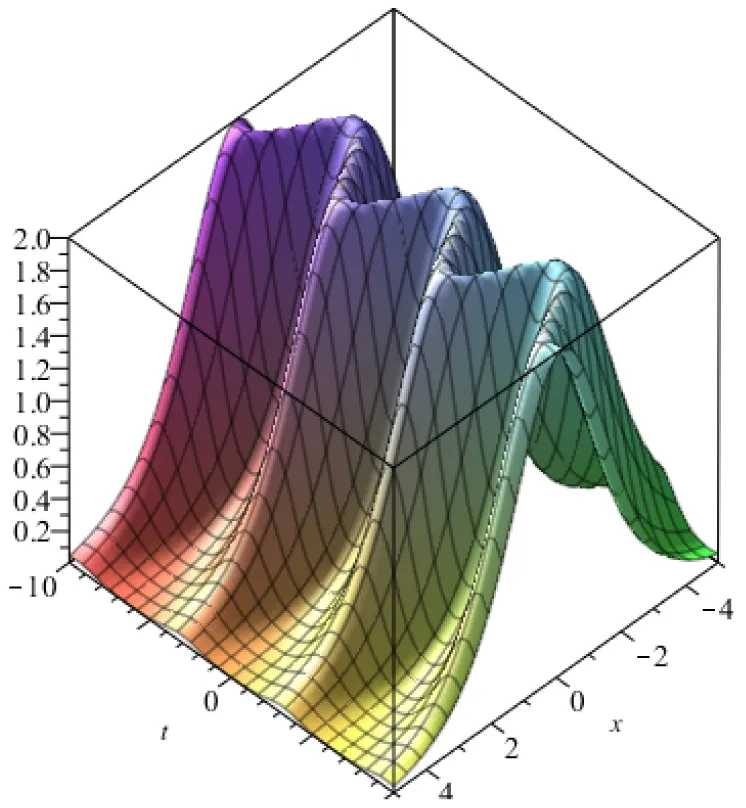
图1 (11) for λ=2,l=0.5 ,k(t)=sint
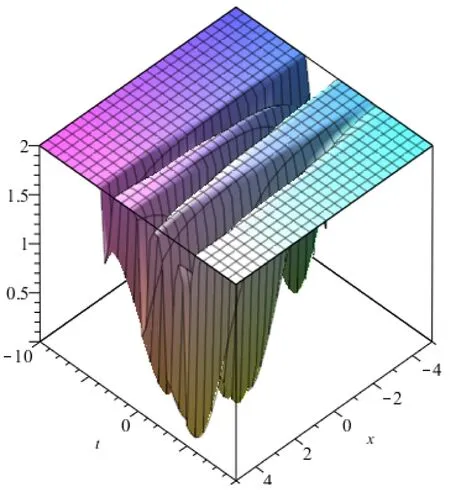
图2 (21) for λ=2,l=0.5 ,k(t)=cost
3 结束语
运用拟设函数法获得变系数5阶KDV方程的光孤子解,包含sech函数形式的亮孤子解和tanh函数形式的暗孤子解,扩大了解的范围,对于研究非线性发展方程具有非常广泛的应用意义,这种方法简洁方便,值得推广。
[1] COHEN B,KROMMES J,TANG W,et al.Non-linear saturation of the dissipative trappedion mode by mode coupling[J].Nucl.Fusion,1976,16:971-992.
[2] SCHRÖDING E.An Undulatory Theory of the Mechanics of Atoms and Molecules[J].Phys Re,1926,28:1049-1070.
[3] FISHER R A.The wave of advance of advantageous genes[J].Ann Eugenics,1937,7:355-369.
[4] WANG M L.Exact Solutions for a Compound Kdv-Burgers Equation[J].Physics Letters A,1996,213(5-6):279-287.
[5] 王明亮,李志斌,周宇斌.齐次平衡原理及其应用[J].兰州大学学报:自然科学版,1999,35(3):8-16.
[6] TAGHIZADEH N,MIRZAZADEH M,FILIZ T.The first-integral method applied to the Eckhaus equation[J].Applied Mathematics Letters,2012,25(5):798-802.
[7] 套格图桑,伊丽娜.广义Zakharov-Kuzentsov方程的类孤子新解[J].量子电子学报,2015,35(3):290-299.
[8] 冯庆江,肖绍菊.应用改进的(G′/G2)-展开法求Zakharov方程的精确解[J].量子电子学报,2015,32(1):40-45.
[9] 庞晶,靳玲花,应孝梅.利用(G′/G)展开法求解广义变系数Burgers方程[J].量子电子学报,2011,28(6):674-680.
[10] ABLOWITZ M J P,CLARKSON P A.Solitons Nonlinear Evolution Equations and Inverse Scattering[M].New York:Cambridge University Press,1991.
[11] 曾昕,张鸿庆.(2+1)维Boussinesq方程的Banklund变换与精确解[J].物理学报,2005,54(4):1476-1480.
[12] CHEN B,XIE Y C.An auto-Backlund transformation and exact solutions of stochastic Wick-type Sawada-Kotera equation[J].Chao,Solitons and Fractals,2005,23:243-248.
[13] 王嘉谋,王尚户,何莉敏.变系数5阶Korteweg-de Vries方程的Lax对和自Backlund变换研究[J].江苏科技大学学报:自然科学版,2013,27(3):303-306.
[14] BISWAS A.1 -soliton solution of the K(m,n) equation with generalized evolution[J].Phy Lett A,2008,372(25):4601-4602.
[15] TRIKI H,WAZWAZ A M.Bright and dark soliton solutions for a K(m,n) equation with t-dependent Coefficients[J].Phy Lett A,2009(373):2162-2165.
[16] BISWAS A.1 -Soliton solution of the generalized Zakharov-Kuznetsov equation with nonlinear dispersion and time-dependent coefficients[J].Phys.Lett.A,2009,373(33):2931-2934.
[17] BISWAS A,TRIKI H,LABIDI M.Bright and dark solitons ofthe Rosenau-Kawahara equation with power law nonlinearity[J].Phys.Wave Phenom,2011(19):24-29.
[18] TRIKI H,ISMAIL M S.Soliton solutions of a BBM(m,n) equation with generalized evolution[J].Appl.Math.Computat,2010,217(1):48-54.
Optical Soliton Solutions for the Fifth-order Variable-coefficient Korteweg-de Vries Equation
YUANPing1,DENGWeiping2
(1.Basic Courses Department,Yangtze University College of Art and Science, Jingzhou 434020, China;2.Mathematics Teaching Center, Tianfu College of SWUFE, Mianyang 621000, China)
KDV equations can be used to describe the spread of non-uniform transmissive medium soliton in quantum mechanics, nonlinear optics and the field of rivers. It’s also the most typical representative of nonlinear dispersive wave equations. In view of the fifth-order variable-coefficient Korteweg-de Vries equation, fist of all, combining with the homogeneous balance principle and using the ansatz method, when the coefficients of equation are constrained by some conditions, the bright solition solutions with sech function and dark solition solutions with tanh function are obtained; Then, combining with the practical background of the parameters in solutions, selected some special parameters and coefficients, the numerical simulation has been conducted as well as the actual communication form of wave function has been depicted. Compared with the past results, the method is more concise, the results generalize and develop the forms of KDV equation’s solutions. The method can be aslo used to solve the other non-linear wave equations.
optical solitons; homogeneous balance method; variable-coefficient Korteweg-de Vries equation
2016-06-22
湖北省教育厅科研计划项目(B2016461)
袁 萍(1984-),女,湖北潜江人,讲师,硕士,主要从事偏微分方程方面的研究,(E-mail)346323353@qq.com
1673-1549(2016)05-0097-04
10.11863/j.suse.2 016.05.2 0
O175
A

