高黏度树脂在纤维织物中浸渍过程的CFD模拟

方 荀, 周云飞, 沈春银, 戴干策

(华东理工大学化学工程联合国家重点实验室,上海 200237)



高黏度树脂在纤维织物中浸渍过程的CFD模拟

方 荀, 周云飞, 沈春银, 戴干策

(华东理工大学化学工程联合国家重点实验室,上海 200237)

采用VOF(Volume of Fluid)方法结合多孔介质模型对树脂在纤维织物中的流动前沿进行追踪,并对截留在纤维织物中的气泡进行捕获。纤维织物中的气泡主要由结构不均匀性造成,结构的不均匀性导致流体速度差异并形成多个流动前沿,气泡在动压的作用下会发生迁移。研究了压力、黏度以及双尺度孔隙率对浸渍速率的影响,发现浸渍时间和压力成反比,和黏度以及纤维束孔隙率与横向渗透率的比值成正比;纤维织物的浸渍速率主要取决于微观浸渍速率,而与纤维束的间距无关。

数值模拟; 气泡; VOF; 多孔介质; 浸渍时间

在纤维增强复合材料中,气泡的存在对复合材料的力学性能有着很大影响,当气泡体积分数小于4%时,气泡体积分数每增加1%,复合材料的层间剪切强度降低7%[1],因此减少甚至消除复合材料中的气泡是复合材料成型的重要目的。排除气泡的过程又被称为浸渍。气泡产生的因素如下:一种为挥发物所导致的气泡[2],主要由环境湿度引起,研究认为高成型温度下,吸湿对热塑性复合材料的气泡形成有很大影响。另一种为纤维毡的不均匀性所导致的气泡形成[3],对于纤维织物,存在两个尺度的流动,即纤维束内和纤维束间的流动,其流速的差异会导致气泡裹挟。

对热固性复合材料的浸渍过程,有大量学者进行了相关研究,基本是针对RTM(树脂传递模塑)等成型工艺。Chen等[4]基于实验的基础提出了双尺度孔隙率的空气截留模型,在研究树脂通过两束纤维的流动时,将束间通道看成收缩-扩张的喉管,而纤维束表面则可以看作是多孔壁面,进而求解,对纤维束内的流动则通过渗透速率来计算,并将气泡压缩性考虑其中。Patel等[5]提出了双通道多孔介质模型,并用两相Darcy定律来求解。Chang等[6]构建了2-D模型研究单向排列的纤维毡的横向流动,他们考虑了两种形式的流动,绕着纤维束的宏观流动和绕着纤维的微观流动,使用单相Darcy定律进行计算,流体前沿压力可以为真空、一个大气压或者毛细压力,当宏观流动的渗透率和微观流动的渗透率之比超过20,则会在纤维束内形成椭圆形的气泡。Kang等[7]提出了一种数学模型,研究RTM成型过程中的气泡形成,认识到不均匀的速度场是由纤维预制体结构的不均匀性所导致的,其中速度和毛细压力的作用可用毛细数来表示,通过校正,该模型可以预测孔隙含量和尺寸。

随着计算机技术的发展,使用数值模拟的方法研究热固性复合材料成型过程中气泡的形成和排除越来越普遍。其中有限元(FE)/控制体积(CV)用来解决充填问题已经非常通用和高效,求解区域使用固定的有限元网格,控制体积由网格节点决定,每个控制体积包含一个与之相关的填充因子。Simacek等[8]使用该方法求解了双尺度多孔介质的流动问题,其中大孔道可以使用一般的Darcy定律和质量守恒来求解,而小孔道的求解则使用汇项。Lawrence等[9]在此基础上添加了毛细作用力的影响,Tan等[10-11]进一步研究非等温过程和反应过程。Lee等[12]则提出了一种真实时间模拟的方法来对空气泡的形成和运动进行控制,使用光学传感器检测流动前沿,实时计算流动前沿的可能发展,并根据发展调整压力,从而降低气泡的含量。VOF方法同样有着比较广泛的应用,常用来模拟模腔中的树脂流动前沿。Yang等[13]针对单向排列的纤维预制体,在纤维束内使用Brinkman方程,纤维束间使用Stokes方程求解,使用VOF方法追踪气液界面。Devalve等[14]使用VOF方法结合多孔介质模型模拟了纤维织物中气体含量的变化,得到最小气含量的工艺条件。Lundström等[15]则使用Level set方法对无褶皱编织纤维中的树脂流动前沿进行模拟。

热塑性复合材料的浸渍研究也有不少,但大多数是模型计算,文献[16-19]提出了关于粉体浸渍或者混合纱的浸渍模型。Steggall等[20]提出了纤维织物熔体浸渍模型,Jespersen等[21]提出了薄膜叠层浸渍模型,考虑了纤维的运动。在热塑性复合材料双钢带压机连续成型过程中,一定压力下树脂熔体在纤维织物的厚度方向上渗透,在这一过程中,热塑性树脂在纤维束内和纤维束间的流动速度不同,使气泡截留。气泡的形成和迁移通过模型的计算不能直观显示出来,通过CFD数值计算不仅可以计算浸渍时间,同时可以观察气泡的形成和迁移。本文采用VOF方法对气液两相界面进行追踪,对宏观的压力、熔体的物性以及纤维织物的结构等因素的影响进行探索。

1 模拟对象及数学模型

1.1 物理模型

本文主要基于无褶皱双轴向纤维织物的几何结构,其代表单元中包含相互垂直的两束纤维,且为多层结构。纤维束的边缘假设为抛物线形,如图1所示。其中纤维束内包含成百上千根纤维单丝,将其看成具有一定孔隙率的多孔介质,在纤维轴向和横向上具有不同的渗透率,该渗透率为孔隙率和纤维半径的函数。树脂在压力的作用下从织物上方渗流,树脂在该纤维织物代表单元中的流动前沿则使用VOF方法[22]进行追踪。VOF是一种基于固定网格的方法,它定义了一个流体体积函数,即网格单元中目标流体体积和网格体积之比(α),通过该流体体积函数来确定自由面,追踪流体的变化。很显然α的范围可以从0到1变化,其中α=0表示该网格单元中全部为空气,α=1表示网格单元中全部为流体,0<α<1时则为交界面单元。

图1 无褶皱纤维织物的几何模型Fig.1 Geometric model of non-crimp fabrics

1.2 纤维束间的流动

纤维束间的通道比较大,可以看成宏观通道,因此使用常规的层流VOF模型即可。流体体积分数守恒方程为

(1)

忽略重力的作用,总体质量守恒方程和动量守恒方程为

(2)

(3)

其中:ρ为流体和空气平均密度,ρ=αρr+(1-α)ρa;μ为黏度,树脂熔体假定为牛顿流体,μ=αμr+(1-α)μa。

1.3 纤维束内的流动

由于纤维束是由许多根单向排列的纤维构成的,纤维之间构成了它的流动通道,该通道的尺寸比较小,一般为微米尺度,因此可看成是微观通道。该微观通道中的流动可以使用多孔介质模型来计算。Darcy定律常常用来计算多孔介质中的流体流动,将Darcy定律中的多孔介质黏性阻力添加到动量源项,忽略惯性阻力,动量守恒方程可以写成:

(4)

1.4 纤维束渗透率

对于单向排列的纤维束,很早就有学者对渗透率进行了研究,Happel[23]取圆形的代表单元,将圆柱边界指定为零剪切应力,获得了纤维轴向和横向流动的渗透率。后来的学者开始用非圆形的代表单元,如正方形排列或六边形排列,求解Stokes方程,获得一系列渗透率与纤维半径a、孔隙率φ的关系。Gebart[24]得到:

(5)

(6)

1.5 边界条件

树脂熔体从上表面以一定的压力流入纤维织物,入口设为压力入口,压力值为p0,纤维织物的下表面为出口,压力始终保持一个大气压,表压为0,因此出口边界条件为压力出口,压力值为0。四周由于具有对称性,因此周围4个面为对称平面,设置为对称边界条件。当t=0时,纤维织物的孔隙中无树脂熔体,因此树脂体积分数α=0,而入口处一直保持α=1。

1.6 数值模拟环境

采用商用软件Fluent14.0,用有限体积法模拟,其中多相流模型选择VOF两相模型,纤维束区域设置为多孔介质。对VOF瞬态计算,压力-速度耦合方法采用PISO,压力离散格式为PRESTO!,速度离散采用二阶迎风格式,相体积分数离散采用Geo-Reconstruct方法,时间离散采用一阶隐式。计算方程残差设为10-3。时间步长采用可变时间步长,最大时间步长为1.0×10-3s,最小时间步长为1.0×10-9s,CourantNumber保持1.0。

1.7 网格划分及其无关化

纤维束区域一共由6个体构成,其中包含2个1/2纤维束和4个1/4纤维束,其网格划分方法为Cooper方法,即在纤维束的端面上划分三角形网格,并沿着纤维束轴扫描,构成楔形网格。纤维束间的区域为了便于划分Cooper网格,将其分割成3个体,其中2个沿着x方向扫描,1个沿着z方向扫描。划分Cooper网格的优点主要为网格生成比较规则,网格质量较高。

图2 无褶皱纤维织物代表单元网格划分Fig.2 Mesh of representative unit of non-crimp fabrics

图3 网格无关化检验Fig.3 Mesh independence

2 结果与讨论

2.1 气泡形成与运动

本文采用的无褶皱双轴向纤维织物代表单元长度L=3 mm,厚度h=1 mm,纤维束的宽度w=2.6 mm,纤维束重叠部分宽度w′=2 mm,代表单元上方有熔体在p0=1.0 MPa的压力作用下向下流动,熔体假定为牛顿流体,黏度μ=2.5 Pa·s。纤维束的孔隙率φ=0.5,纤维半径a=20 μm,此时可以通过关系式求得纤维束轴向的渗透率K∥=3.02×10-11m2,横向的渗透率K⊥=6.54×10-12m2。由于纤维束间的通道比纤维束内的大很多,因此树脂熔体会优先通过束间的通道,并同时缓慢地向纤维束内渗透。正是由于两者之间的速率差异显著,纤维束间快速流动的树脂会对纤维束内的空气进行围追堵截,从而形成了气泡,如图4所示。实际上,纤维束内部会产生毛细作用力,如果毛细作用力够大的话,也可能导致纤维束内的流动快于纤维束间的流动,从而使得气泡被截留在纤维束间,本文中由于树脂的黏度比较大,因此忽略毛细作用力的影响,气泡一般形成于纤维束内。

图4 热塑性复合材料中气泡的形成Fig.4 Bubble formation in thermoplastic composites

液体浸渍纤维束间宏观通道的速度非常快,在t=0.000 3 s时就已经将上层的宏观通道完全填充,而下层的宏观通道浸渍速度并不快,其原因可以通过流线进行解释。图5所示为z=0平面上不同时间的相分布情况。图6所示为从宏观通道流入流体的流线,该宏观通道类似于一个喉管,树脂熔体收缩进入喉道,从喉道出来的流体只能向两边到达一定的距离,因此t=0.000 3 s时下层宏观通道并不能完全填充。下层的宏观通道如果需要继续被填充,需要通过渗入纤维束中的流体来实现,随着渗入纤维束的熔体越来越多,下层宏观通道能到达的区域则越远,图5中0.01～0.05 s反映了这一现象。微观通道中的流体通过宏观通道缓慢向其渗透,沿着纤维束周围渗透的树脂逐渐排除其中的空气,因此宏观通道也必须留出通道使空气排出。

图7所示为z=1 mm平面上不同时间的相分布情况。当t=0.000 3 s时,树脂已经通过宏观通道将中心处填充,而上方纤维束中的树脂由于多孔介质黏性阻力的作用渗透较慢；当t=0.002 s时,宏观通道中的树脂向周围的纤维束横向渗透,当两股流体前沿相遇时,则裹挟了一段气泡。接着气泡受到流体的挤压由扁平状收缩为三角状,并从纤维束内向纤维束间迁移,接着被驱赶进入下层的纤维束内,同时又被挤压成扁平状,在t=0.05 s时,该气泡被排除。两侧纤维束中的空气则不断被渗入的树脂所排挤,从边缘处被排出。

图5 z=0处树脂相分布图Fig.5 Resin phase distribution at z=0

图6 宏观通道的流线和x-y平面投影图Fig.6 Streamline of macro channels and projection at x-y plane

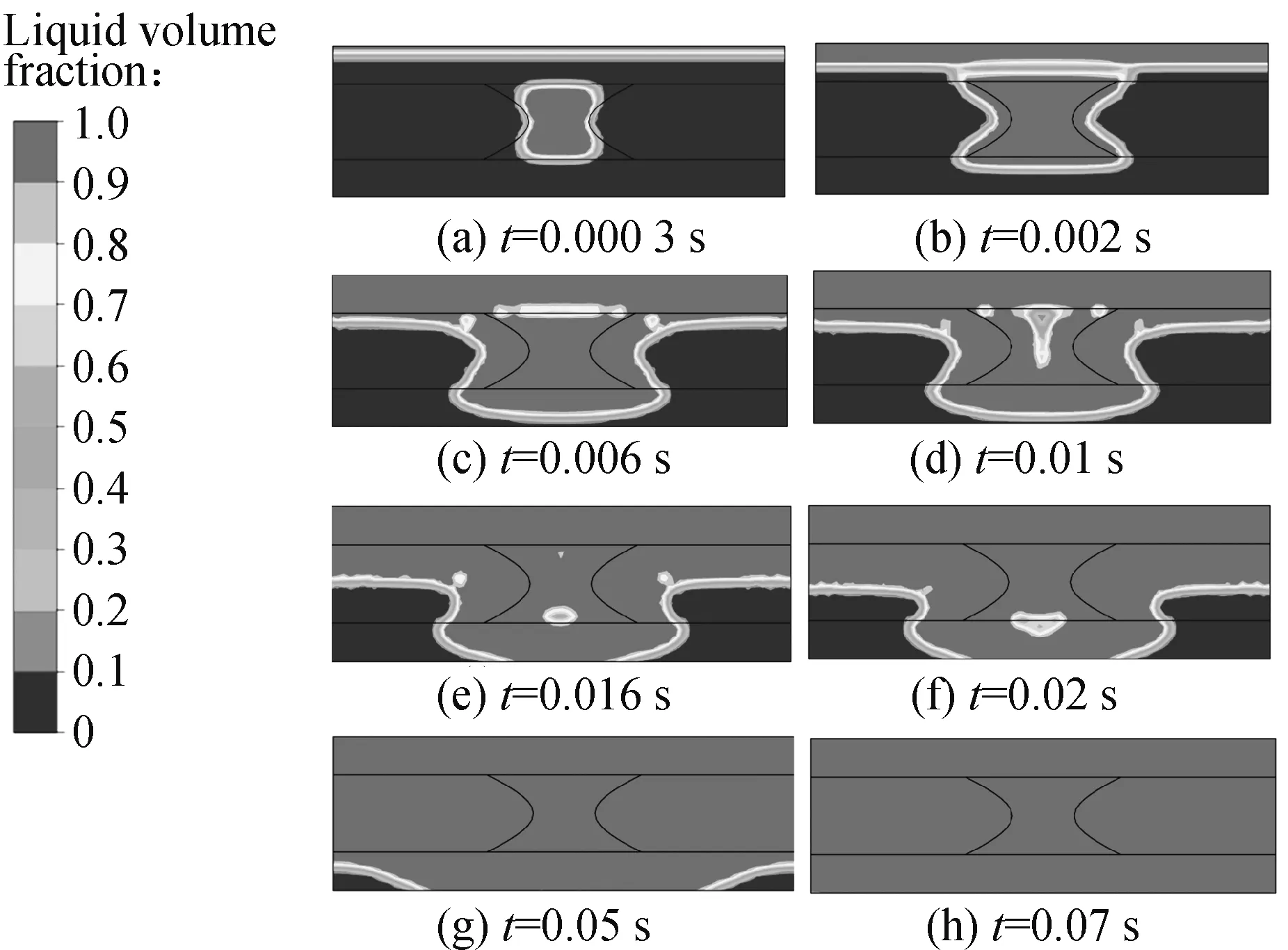
图7 z=1 mm处树脂相分布图Fig.7 Resin phase distribution at z=1 mm

考虑到纤维床中的气泡周围被树脂包围,其外部和内部的压力是平衡的,气泡的自由面具有相同的曲率。当树脂受到驱动时,会产生额外的动压和黏性应力场,并导致自由面曲率发生变化,下游方向的曲率增大,上游方向的曲率降低,从而使压差适应外界的压力梯度,然而自由面对压力的调整是有限的,一旦外界的压力梯度超过了自由面的可调整范围,那么气泡就开始运动。因此,当气泡两端的毛细压差小于动压,则气泡就会移动,反之,气泡则不会被排出。毛细压差(Δpcap)为

(7)

其中σ为表面张力。而黏性流动导致的压差(Δp)为

(8)

其中,θ为气泡长度与来流方向的夹角。如果Δp/Δpcap>1,则气泡可以移动。对复合材料中的气泡迁移过程,Gangloff等[25]通过数值计算发现,对于给定尺寸的气泡,一定的操作条件可以通过毛细管数来决定气泡能否迁移,很显然和上面的分析相符合。在热塑性复合材料中,由于黏性流动所导致的压差一般大于毛细压差,因此气泡能够发生迁移。

图8所示为x=0平面上不同时间的相分布图。结合图7和图8可以看出,气泡在纤维织物中的流动方向和树脂的流动方向基本一致。气泡刚从纤维束内进入纤维束间时,气泡在向下迁移的同时向两侧运动,当气泡从纤维束间又进入下层的纤维束内时,气泡在向下迁移的同时又向中心运动,可以看出气泡的迁移主要受流体黏性压差的作用驱动。同时可以发现气泡在迁移的过程中会发生破裂,特别是由纤维束间到纤维束内时,大气泡分裂成小气泡再排出。

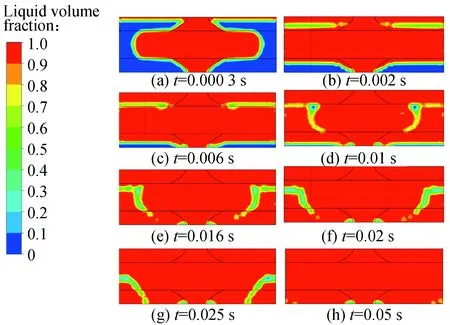
图8 x=0处树脂相分布图Fig.8 Resin phase distribution at x=0

图9所示为纤维束间、纤维束内和整个纤维织物中的树脂体积分数随时间的变化。很显然,纤维束间的浸渍时间很短,而纤维束内的浸渍时间相对较长,而整个纤维织物的浸渍时间主要取决于纤维束的浸渍时间。纤维束间在0～0.000 3 s之间树脂体积分数变化很快,而在0.000 3～0.05 s之间仍有一段缓慢增长,这是由于下层的宏观通道并不能迅速填充完全,和图4所显示的情况相符。

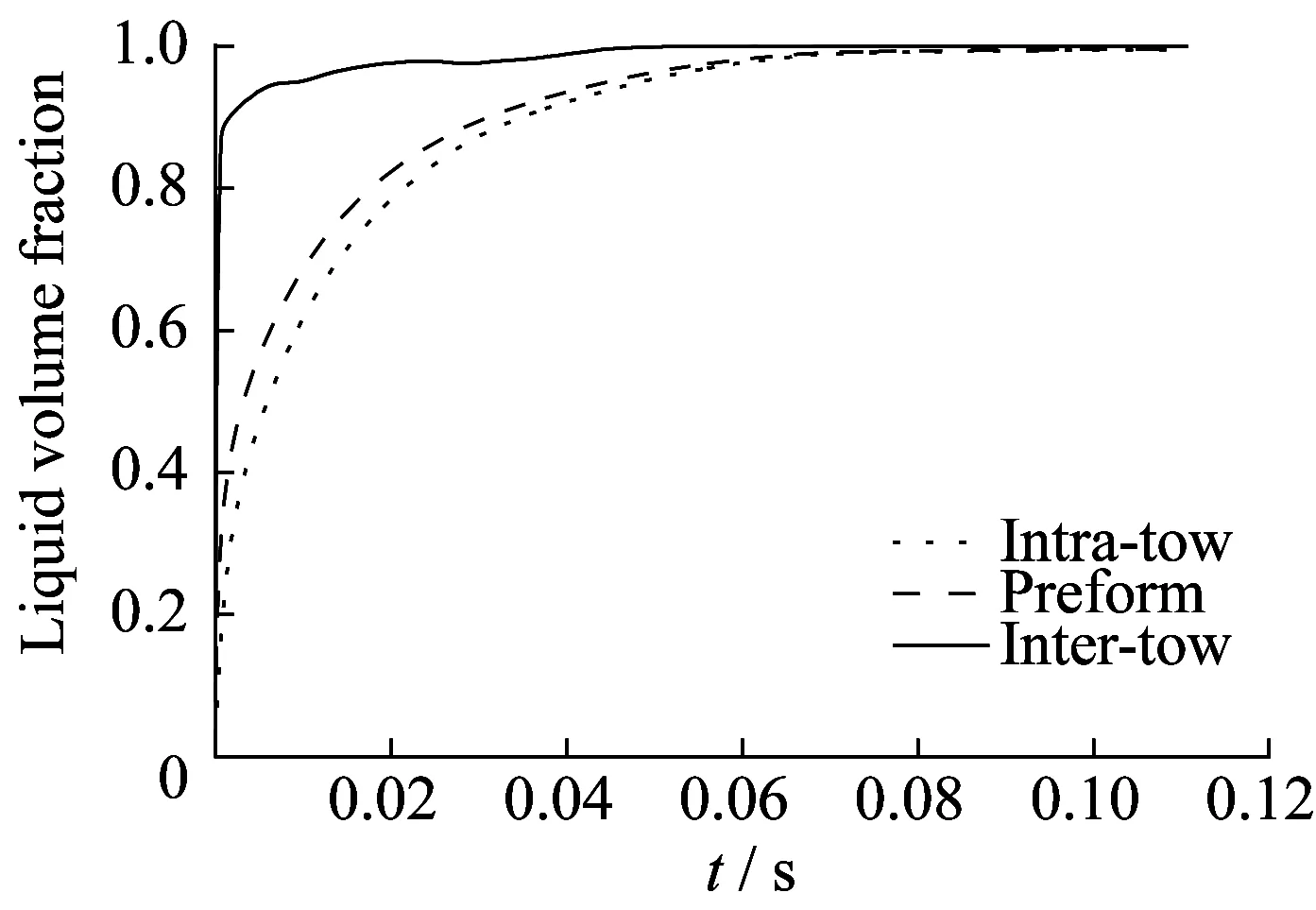
图9 纤维束间、纤维束内、预制体中 树脂体积分数与时间的关系Fig.9 Volume fraction of resin in intra-tow and inter-tow and preform vs. time

热塑性复合材料中的气泡形成主要是由于纤维织物中局部阻力不同导致流速差异,从而产生多个流动前沿,由于宏观通道的流速大于微观通道,因此流动前沿一般在纤维束内相遇,从而截留气泡。由于热塑性复合材料中的黏性流动产生的压差大于毛细压差,因此气泡能够发生迁移,只要时间足够长，气泡就可以被排除,这意味着保压时间对于气泡的排除十分重要。需要注意的是,延长保压时间虽然能够将气泡含量降低到最低值,但对工业上需要的高效率生产方式相违背,此时可能需要权衡制品质量和保压时间的关系。就本例而言,当树脂体积分数达到0.90时需要的时间为0.03 s,达到0.95时所需要的时间延长50%,达到0.99时所需的时间延长100%,而达到0.995时所需的时间延长200%,由此可见浸渍过程越往后时间越长,如果制品的气含量能够允许0.5%,浸渍时间只需要0.09 s即可。

2.2 压力对浸渍速度的影响

随着压力的增加,树脂在纤维织物中的流速也增加,因此排除空气的速度会加快。图10示出了不同的压力对树脂充填速度的影响。压力对宏观通道的浸渍影响不太显著,如图10(b)所示,因为宏观通道中的流速很快,在3×10-3s之前树脂体积分数就超过0.9,最终的差别仅仅是下层的宏观通道的浸渍速率。对比图10(a)和图10(c),压力对微观通道浸渍速率和纤维织物整体的浸渍速率基本一致,可见整个纤维织物的浸渍速率取决于纤维束的浸渍速率。纤维束内的浸渍速率又基本取决于横向的浸渍速率,这是因为横向的渗透率要比轴向渗透率低。

图10 压力对树脂浸渍速度的影响Fig.10 Effects of pressure on impregnation velocity

纤维束模型常常使用矩形或者圆形。假设纤维束为矩形,如图11所示,纤维束横向渗透速率和压力的关系可用Darcy定律来表示。

(9)

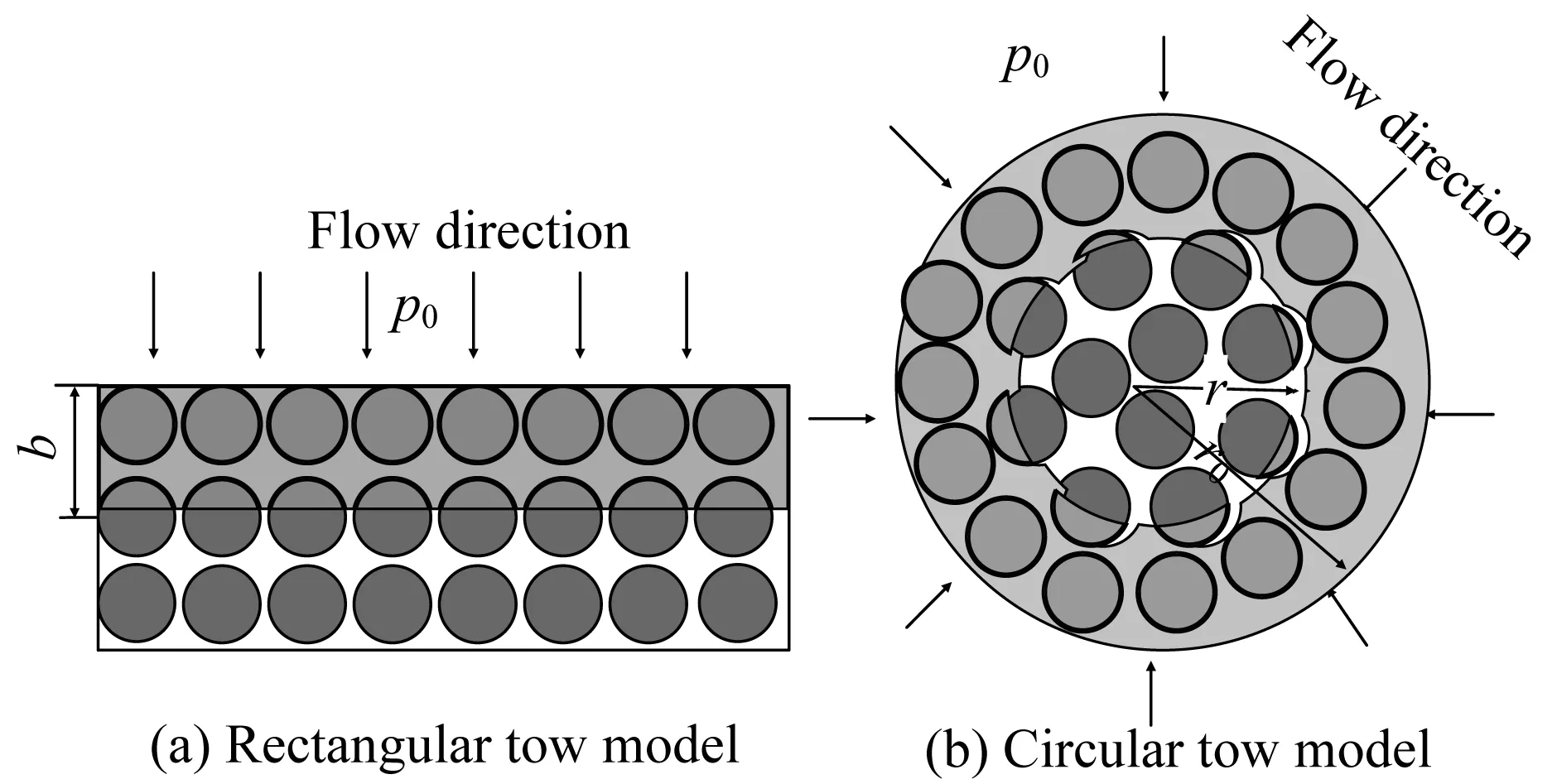
图11 矩形纤维束模型和圆形纤维束模型Fig.11 Rectangular and circle models of fiber tows

因此,可求得浸渍时间分析解为

(10)

其中,b为树脂渗入纤维束的距离。如果假设纤维束为圆形,流体从四周向中心渗透,Darcy定律写成柱坐标形式为

(11)

其中,径向流动的压力梯度为

(12)

通过积分求得浸渍时间随流动前沿变化的分析解为

(13)

对一般形状的纤维束,可以得到推广的浸渍时间:

(14)

对于给定的纤维织物结构,由于纤维束的几何形状、尺寸和树脂流动方向基本不变,可认为f(φ)仅是总的树脂体积分数φ的函数。图10(d)中示出了不同树脂填充体积分数下浸渍时间和压力的关系,也可以发现其变化规律基本和上述的分析结果相符,即在相同的树脂体积分数下,浸渍时间和压力的乘积是定值。对该纤维织物而言,压力增大到一定程度时,浸渍时间的变化则不太明显,压力从0.5 MPa增加到1.0 MPa,树脂体积分数达到0.99时的浸渍时间降低了50%,而压力从0.5 MPa增加到1.5 MPa时,浸渍时间降低66%,和50%相比变化不大,因此在压力和浸渍时间中权衡的话,1.0 MPa的压力比较合适,继续增加压力虽能降低浸渍时间,但意义不显著。

2.3 树脂黏度对浸渍速率的影响

树脂黏度对浸渍时间的影响很大,黏度越大意味着黏性阻力越大,从之前的分析可知,浸渍时间主要取决于纤维束内的浸渍时间,在本文中为纤维横向的浸渍时间。不管是矩形还是圆形的纤维束模型,在获得同样的树脂体积分数条件下,浸渍时间都与黏度成正比,如图12所示。在本文的物理模型中,并没有忽略惯性项的计算,而实际的结果表明,在该黏度范围惯性项的作用可忽略,只考虑黏性项时,对宏观通道的流动仅用Stokes方程,而对微观的纤维束内的流动则使用Darcy定律即可。此时,从方程上也可以得到在相同的压力下,流速与黏度成反比,因而浸渍时间和黏度成正比。这一结果仅针对黏度较高的情形,对于热固性树脂,因为不可忽略惯性项,浸渍时间也就与黏度不成正比。当然,针对实际的聚合物熔体,简单的牛顿黏性定律不能充分描述流体的性质,常常使用剪切稀化或者黏弹性本构方程描述,因此实际的情况将更加复杂。需要说明的是,热塑性树脂的真实黏度比本文设定的黏度还要高一到两个数量级以上,本文设定的黏度虽远高于一般热固性树脂的黏度,但仍存在缺憾。从图12(b)看出,当树脂体积分数达到0.99,黏度从1.5 Pa·s增加到4.5 Pa·s时,浸渍时间从0.04 s增加至0.12 s,可以预计到当黏度提高一到两个数量级后,浸渍时间会增加几十甚至上百倍,此时可以通过提高压力的方法来缩短浸渍时间。

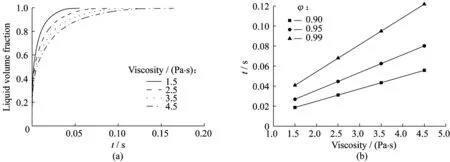
图12 树脂黏度对浸渍速率的影响Fig.12 Effects of viscosity on impregnation velocity

2.4 孔隙率对浸渍速率的影响

在纤维织物中包含了宏观通道和微观通道两种尺度的通道,因此它包含了两种尺度的孔隙率：一种为大孔孔隙率,另一种为微孔孔隙率,它们都会对树脂的浸渍以及气泡的形成产生影响。本文对纤维束中的微孔采用多孔介质方法,大孔采用真实的通道进行模拟。纤维束的孔隙率越大,横向和轴向的渗透率越大,当纤维束完全紧密堆积时,横向的渗透率则减为零,而轴向仍可以大于零。图13所示为通过经验式得出的横向与轴向渗透率随孔隙率的变化关系。当纤维束孔隙率在0.4～0.7变化时,横向渗透率与轴向渗透率之比在5左右。当孔隙率减小时,横向渗透率会产生突降,而轴向渗透率降低相对较慢,两者之间差别可达多个数量级。如果纤维束排列特别紧密,横向渗透将非常困难,尤其本文中树脂的主流动方向即为纤维束横向流动,纤维束排列不能过于紧密,否则浸渍时间会增加多个数量级。

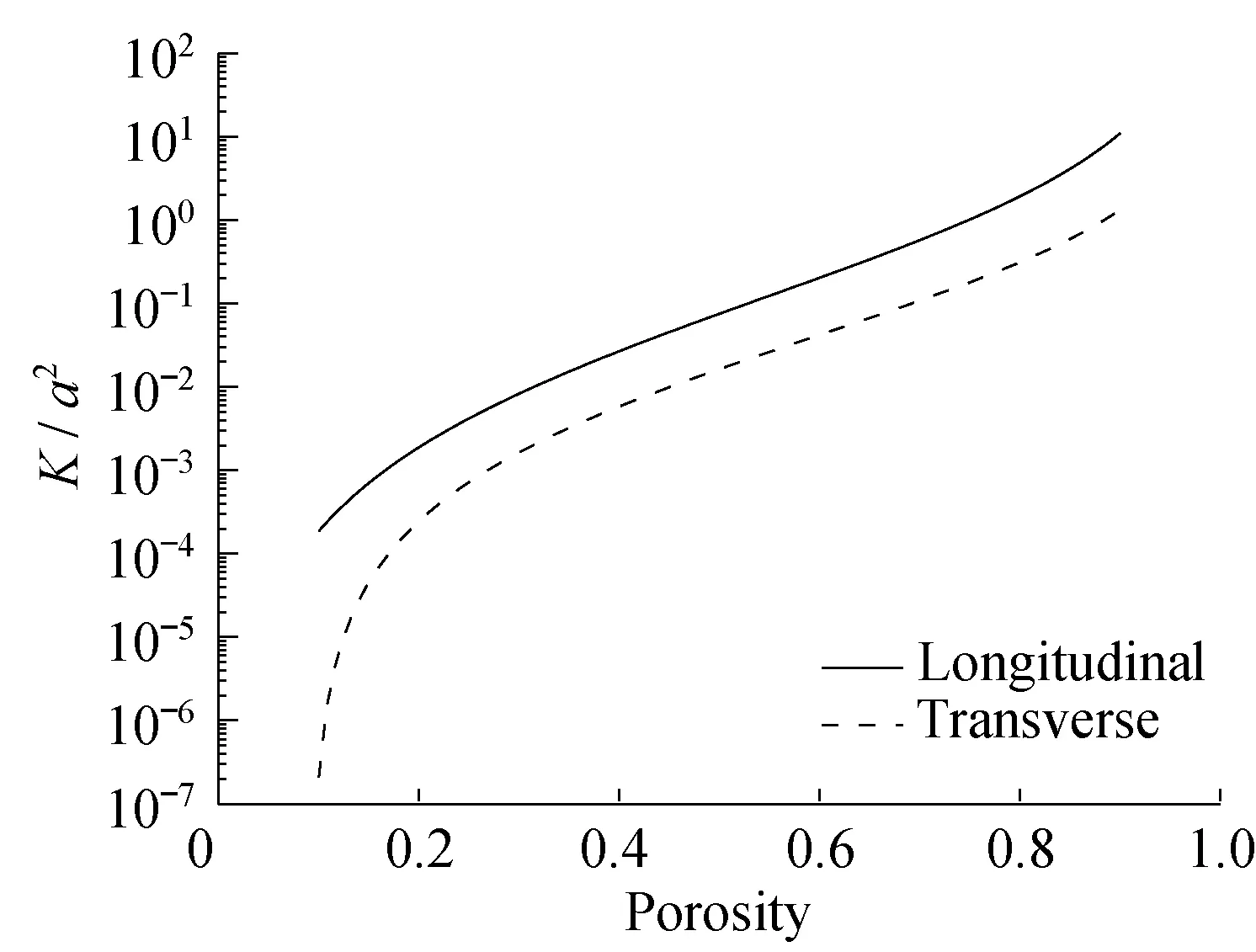
图 13 纤维束轴向和横向渗透率与孔隙率的关系Fig.13 Relationship between axial,transverse permeability and porosity

图14所示为纤维束孔隙率对浸渍速率的影响。很显然，随着孔隙率的增大,纤维束的渗透率增大,黏性阻力降低,有利于微观浸渍。由于纤维织物的浸渍速率主要取决于纤维束的浸渍速率,因此孔隙率增大,微观浸渍速率加快,同时整个纤维织物的浸渍速率也随之加快。为了更好地预测纤维束孔隙率对浸渍时间的影响,结合式(14)将浸渍时间和孔隙率对横向渗透率的比值(φ/K⊥)作图,可以得出浸渍时间和孔隙率对横向渗透率的比值基本成正比。因此,几何结构相同的条件下,可以估算出不同的纤维束孔隙率浸渍所需要的时间。当纤维束孔隙率从0.7降低至0.4时,相同树脂体积分数下的浸渍时间提高了10倍左右。如果想要获得高性能的复合材料,必须要提高纤维含量,这也意味着纤维束的孔隙率降低,从而浸渍速率降低,加工难度提高,此时需要通过提高温度、降低黏度或者提高压力的方法来提高浸渍速率。

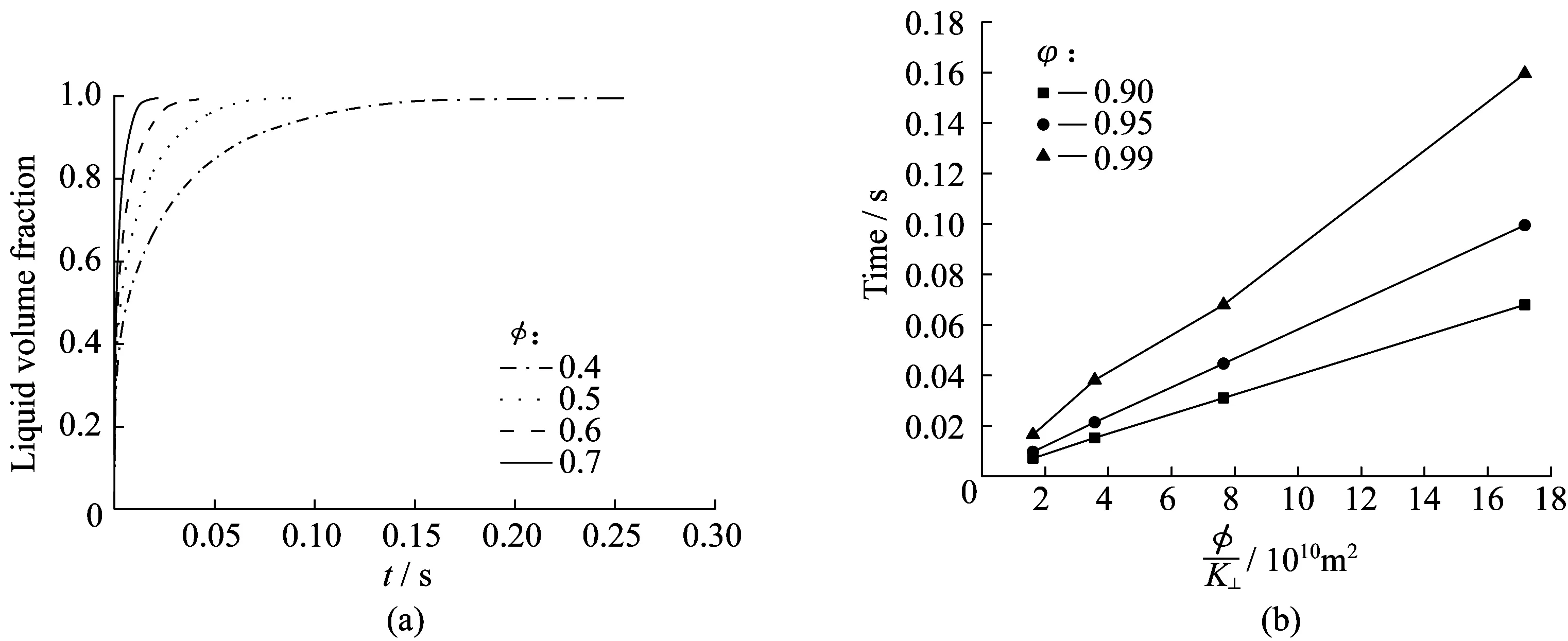
图14 纤维束孔隙率对浸渍速率的影响Fig.14 Effects of porosity of fiber tows on impregnation velocity

除了微孔孔隙率,纤维织物还存在纤维束间的大孔孔隙率。在纤维束尺寸不变的情况下,调整纤维束间的距离,大孔的孔隙率将发生变化。图15显示了不同的纤维束间距离对树脂浸渍速度的影响。很显然,大孔的孔隙率对树脂浸渍速率影响很小,尤其间距d从0.4 mm到0.6 mm变化时,几乎不变,这是因为当d=0.2 mm时,宏观通道的尺寸相对较小,流动阻力较大,因此宏观通道的浸渍速率仍然会对整个纤维织物的浸渍速率产生微量的影响,而随着纤维束的间距的增大,宏观通道的浸渍速率变快,整个纤维织物的浸渍速率几乎只取决于微观浸渍速率,因此它们的浸渍速率曲线几乎重合。但总体来说,纤维织物的浸渍速率还是取决于微观浸渍速率,与之前的分析一致。

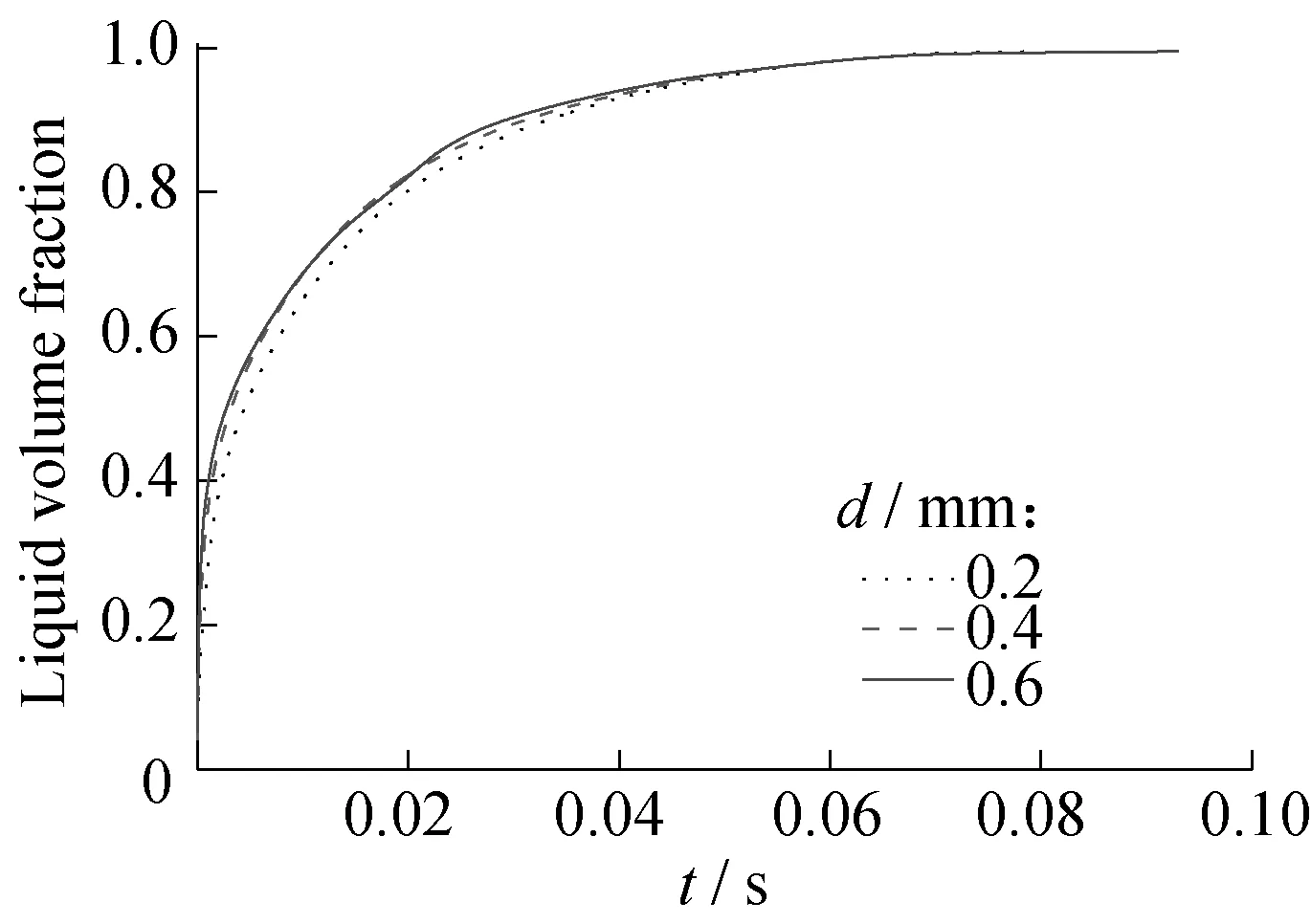
图15 纤维束间距对浸渍速率的影响Fig.15 Effects of tow gaps on impregnation velocity

此外,随着纤维束间距的减小,受到截留的气泡运动速度反而加快,图16对比了3种纤维束间距的受裹挟气泡的迁移情况。在t=0.03 s,间距d=0.2 mm时,纤维束间和纤维束内被截留的气泡几乎都被排除;当d=0.4 mm时,被截留的气泡仍然存在,但已经向下迁移到纤维束中,并处于排除状态;d=0.6 mm时,被截留的气泡还停在纤维束间的通道中。可以看出d=0.2 mm截留气泡迁移的速度大于d=0.4 mm,气泡迁移速度最慢的是d=0.6 mm。在宏观通道中,虽然垂直通道中的速度规律是随着纤维束间距的减小而降低,但是在水平通道中,速度却随着纤维束间距的减小而有所上升。

图16 t=0.03 s时的相分布图 (z=0)Fig.16 Phase distribution at t=0.03 s (z=0)

图17的速度分布图可以说明这一情况。从总体速度云图来看,显然间距越大,在垂直通道中的流速越快,从局部速度云图可以看出,间距越小在水平通道中的流速越快,因此流体驱赶气泡的速度也会变大,气泡反而更容易排出。

图17 总体速度和局部速度(0～0.2 m/s)云图(z=0)Fig.17 Global and local (0～0.2 m/s) velocity contour (z=0)

2.5 模型验证

本文主要采用VOF结合多孔介质模型的方法对纤维多孔介质中的气-液两相流动进行模拟,为了验证CFD模型的正确性,对多孔介质方腔,分别采用数值计算和模型公式求解时间和填充分数的关系,如图18所示。其中多孔介质渗透率为1.0×10-9,孔隙率为0.5,树脂黏度为5 Pa·s,方腔长度为10 mm,宽度为5 mm,树脂沿着方腔长度方向流动,压力为105Pa。和式(10)类似,推导求得时间和填充分数的关系为

(15)

对比用式(15)和CFD方法得到的时间与树脂填充分数的关系,可以发现,采用CFD方法求解的结果和模型公式所得结果吻合很好,可以证明采用VOF追踪气-液界面的方法在多孔介质中是适用的。

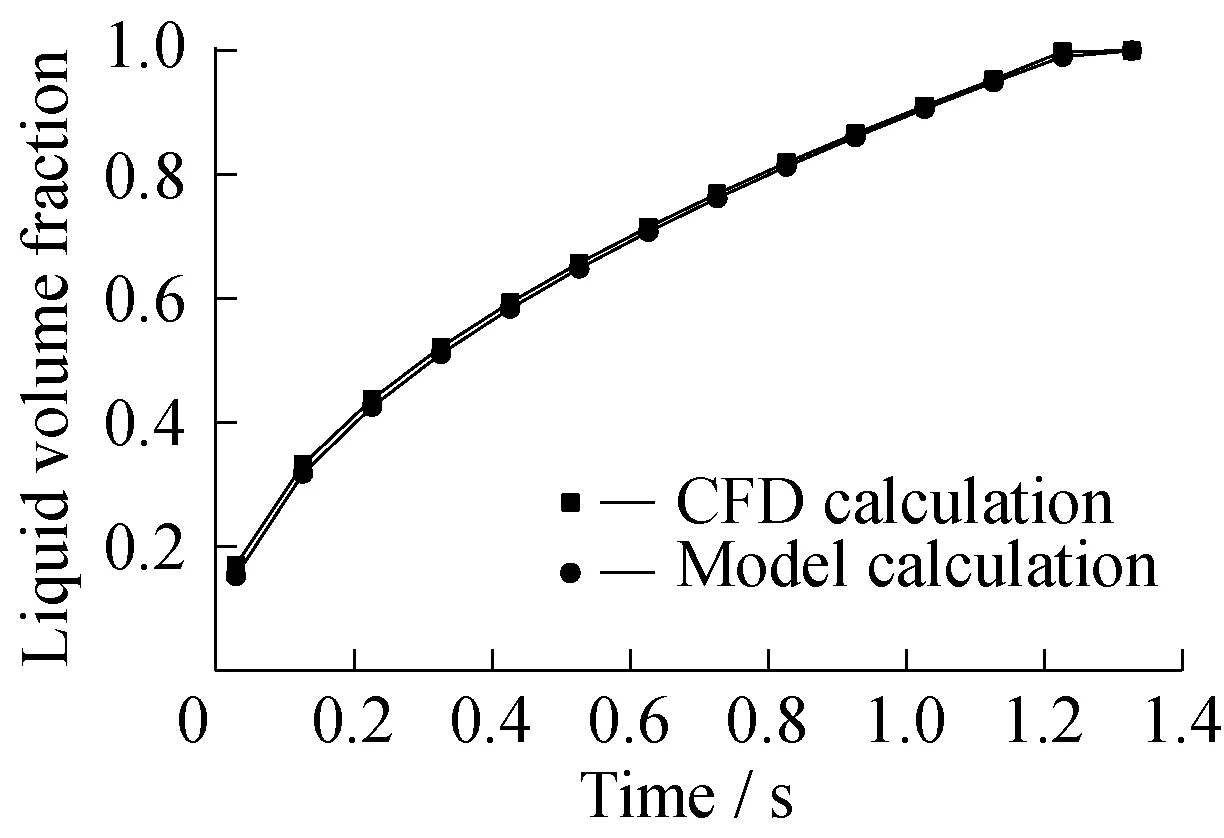
图18 模型法和CFD结果对比Fig.18 Comparison between CFD and model results

Wang等[26]对双钢带压机的运行速度和浸渍效果进行了定量测试,如果将运行速度转化为浸渍时间,即运行速度正比于浸渍时间的倒数,Wang得到的孔隙率随浸渍时间的变化趋势和本文模拟得到的变化趋势基本一致。

3 结 论

本文采用数值模拟方法对无褶皱双轴纤维织物代表单元中的树脂浸渍过程进行模拟,其中VOF方法能够追踪气液两相的界面,而纤维束内则采用多孔介质模型进行模拟,纤维束间为一般流动通道。采用CFD方法能够对织物的浸渍进行模拟分析,得到的规律能够对成型起到一定的指导作用。

(1) 纤维束间的宏观浸渍速率比微观浸渍速率大两个数量级,纤维织物的浸渍速率主要取决于纤维束内的浸渍速率。

(2) 树脂对纤维织物的浸渍速率开始时很快,然后不断降低,达到100%浸渍程度的时间相对较长,可以根据气泡含量要求选择浸渍时间,过长的时间会降低生产效率。

(3) 压力越大,浸渍速率越大,获得同样的树脂体积分数所需时间和压力成反比。压力的选择也需要权衡考虑,随着压力的不断增大,它对浸渍速率的影响越来越小,然而它对设备的要求越来越高。

(4) 黏度越大,所需的浸渍时间越长,浸渍所需时间基本和黏度成正比,对于更高黏度的树脂熔体,浸渍时间可能达到几十、上百秒,需要增加浸渍压力来减少浸渍时间。孔隙率从0.7降低至0.4,浸渍时间提高10倍,可考虑适当提高成型温度使黏度降低,或者增加压力来提高浸渍速率。

符号说明:

a——纤维半径,μm

b——树脂渗入纤维束的距离,mm

d——纤维束间距,mm

h——纤维束厚度,mm

K——渗透率张量,m2

K⊥——横向渗透率,m2

K∥——轴向渗透率,m2

L——代表单元长度,mm

l——气泡的长度,mm

p——压力,MPa

p0——入口压力,MPa

pcap——毛细作用力,MPa

r——纤维束浸渍前沿的半径,mm

r0——纤维束的半径,mm

rb——气泡半径,mm

rt——孔隙收缩处半径,mm

t——浸渍时间,s

tcir——圆形纤维束浸渍时间,s

trec——矩形纤维束浸渍时间,s

u——流动速度,m/s

ub——矩形纤维束模型的渗透速率,m/s

ur——圆形纤维束模型的渗透速率,m/s

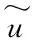
w ——纤维束宽度,mm

w′——纤维束重叠部分宽度,mm

α——树脂相体积分数

ρ ——平均密度,kg/m3

ρa——空气密度,kg/m3

ρr——树脂密度,kg/m3

μ ——平均黏度,Pa·s

μa——空气黏度,Pa·s

μr——树脂黏度,Pa·s

φ ——纤维束孔隙率

φc——紧密堆积时的孔隙率

φ——总的树脂体积分数

[1] JUDD N,WRIGHT W.Voids and their effects on the mechanical properties of composites:An appraisal[J].SAMPE Journal,1978,14:10-14.

[2] ROYCHOWDHURY S,GILLESPIE Jr J,ADVANI S.Computer Aided Design in Composite Material Technology III[M].Netherlands:Springer,1992:89-107.

[3] YU M C,MIDDLEMAN S.Air entrapment during liquid infiltration of porous media[J].Chemical Engineering Communications,1993,123(1):61-69.

[4] CHEN Y T,MACOSKO C W,DAVIS H T.Wetting of fiber mats for composites manufacturing:II.Air entrapment model[J].AIChE Journal,1995,41(10):2274-2281.

[5] PATEL N,LEE L J.Modeling of void formation and removal in liquid composite molding:Part II.Model development and implementation[J].Polymer Composites,1996,17(1):104-114.

[6] CHANG C Y, HOURNG L W.Study on void formation in resin transfer molding[J].Polymer Engineering & Science,1998,38(5):809-818.

[7] KANG M K,LEE W I,HAHN H T.Formation of microvoids during resin-transfer molding process[J].Composites Science and Technology,2000,60(12):2427-2434.

[8] SIMACEK P, ADVANI S G.A numerical model to predict fiber tow saturation during liquid composite molding[J].Composites Science and Technology,2003,63(12):1725-1736.

[9] LAWRENCE J M,NEACSU V,ADVANI S G.Modeling the impact of capillary pressure and air entrapment on fiber tow saturation during resin infusion in LCM[J].Composites:Part A.Applied Science and Manufacturing,2009,40(8):1053-1064.

[10] TAN H,PILLAI K M.Multiscale modeling of unsaturated flow of dual-scale fiber preform in liquid composite molding:II.Non-isothermal flows[J].Composites:Part A.Applied Science and Manufacturing,2012,43(1):14-28.

[11] TAN H,PILLAI K M.Multiscale modeling of unsaturated flow in dual-scale fiber preforms of liquid composite molding:III.Reactive flows[J].Composites:Part A.Applied Science and Manufacturing,2012,43(1):29-44.

[12] LEE D H,LEE W I,KANG M K.Analysis and minimization of void formation during resin transfer molding process[J].Composites Science and Technology,2006,66(16):3281-3289.

[13] YANG J,JIA Y,SUN S,etal.Mesoscopic simulation of the impregnating process of unidirectional fibrous preform in resin transfer molding[J].Materials Science and Engineering:A,2006,435:515-520.

[14] DEVALVE C,PITCHUMANI R.Simulation of void formation in liquid composite molding processes[J].Composites:Part A.Applied Science and Manufacturing,2013,51:22-32.

[15] LUNDSTROM T S,FRISHFELDS V,JAKOVICS A.Bubble formation and motion in non-crimp fabrics with perturbed bundle geometry[J].Composites:Part A.Applied Science and Manufacturing,2010,41(1):83-92.[16] LEE W I,SPRINGER G S.A model of the manufacturing process of thermoplastic matrix composites[J].Journal of Composite Materials,1987,21(11):1017-1055.

[17] BERNET N,MICHAUD V,BOURBAN P,etal.An impregnation model for the consolidation of thermoplastic composites made from commingled yarns[J].Journal of Composite Materials,1999,33(8):751-772.

[18] SALA G,CUTOLO D.The pultrusion of powder-impregnated thermoplastic composites[J].Composites:Part A.Applied Science and Manufacturing,1997,28(7):637-646.

[19] VAN West B,PIPES R B,ADVANI S.The consolidation of commingled thermoplastic fabrics[J].Polymer Composites,1991,12(6):417-427.

[20] STEGGALL-MURPHY C,SIMACEK P,ADVANI S G,etal.A model for thermoplastic melt impregnation of fiber bundles during consolidation of powder-impregnated continuous fiber composites[J].Composites:Part A.Applied Science and Manufacturing,2010,41(1):93-100.

[21] JESPERSEN S,WAKEMAN M,MICHAUD V,etal.Film stacking impregnation model for a novel net shape thermoplastic composite preforming process[J].Composites Science and Technology,2008,68(7):1822-1830.

[22] HIRT C W,NICHOLS B D.Volume of fluid (VOF) method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39(1):201-225.

[23] HAPPEL J.Viscous flow relative to arrays of cylinders[J].AIChE Journal,1959,5(2):174-177.

[24] GEBART B.Permeability of unidirectional reinforcements for RTM[J].Journal of Composite Materials,1992,26(8):1100-1133.

[25] GANGLOFF J J,DANIEL C,ADVANI S G.A model of two-phase resin and void flow during composites processing[J].International Journal of Multiphase Flow,2014,65:51-60.

[26] WANG X,MAYER C,NEITZEL M.Some issues on impregnation in manufacturing of thermoplastic composites by using a double belt press[J].Polymer Composites,1997,18(6):701-710.

CFD Simulation of Impregnation Process with Highly Viscous Resin in Fiber Fabrics

FANG Xun, ZHOU Yun-fei, SHEN Chun-yin, DAI Gan-ce

(State Key Laboratory of Chemical Engineering,East China University of Science and Technology,Shanghai 200237,China)

Flow front in fiber fabrics was tracked by VOF (volume of fluid) method combined with a porous medium model,and the entrapped air bubbles were captured by simulation.The formation of bubbles is due to the heterogeneous structure which causes the velocity difference with several flow front.The bubbles will migrate under the dynamic pressure.Moreover,the effects of pressure,viscosity and dual-scale porosity on impregnation velocity were studied,and the impregnation time was in propotional to the reciprocal of pressure,viscosity,or transverse permeability divided by tow porosity.The impregnation velocity was determined by the impregnation of micro channels while had nothing to do with the distance between two fiber tows.

numerical simulation; bubbles; VOF; porous medium; impregnation time

1006-3080(2016)05-0615-10

10.14135/j.cnki.1006-3080.2016.05.005

2016-05-04

国家自然科学基金(21376086)

方 荀(1989-),男,江苏泰州人,博士生,研究方向为热塑性复合材料加工成型。E-mail:shawnfang@msn.cn

沈春银,E-mail:ichuny@ecust.edu.cn

TB332; TQ021.1

A