企业产品种群规模稳定性和年龄结构优化模型

伊辉勇,凌艳涛

(重庆科技学院工商管理学院,重庆401331)

企业产品种群规模稳定性和年龄结构优化模型

伊辉勇,凌艳涛

(重庆科技学院工商管理学院,重庆401331)

面对同一顾客群体的竞争性企业所提供的产品族谱之间具有相互替代、交叉衍生的互动关系.将企业产品族谱视为产品种群,探求如何确定产品种群的出生率(新产品开发率)和死亡率(老产品淘汰率)以使企业产品种群获得持续活力.建立了不合理产品种群的修正模型,通过产品内部演化的动力学原理,揭示了维持产品稳定的条件和最终稳定状态.在此基础上以产品淘汰量为优化目标,建立了最优种群规模和年龄结构平衡模型.利用线性规划方法,通过控制出生率和存活率来优化产品种群结构,最终使产品种群结构稳定在最优状态.最后仿真验证模型的可行性和有效性.

产品维护复杂性;产品种群;种群规模;年龄结构;线性规划

1　引　言

对于大规模定制环境下的市场客户而言,其需求变化有两大趋势:1)客户需求空间变化越来越快;2)客户需求越来越个性化,换句话说就是企业产品面对的细分市场容量越来越小.作为应对之策,企业必须迅速捕获客户瞬息万变的需求及其变化趋势,同时不断增加产品型谱的规模.然而,不断增加的产品型谱规模势必会增加产品维护难度和管理成本[1].因此,企业在进行产品研发决策的时候必须考虑:1)产品型谱如何优化才能使产品型谱始终保有较高的竞争力,同时又不会超出企业产品开发和维护的能力;2)产品型谱应该如何更新换代才能始终较好地满足客户需求.为了解决上述问题,本文探讨企业如何在保证产品型谱规模稳定性的前提下不断优化产品的年龄结构.

种群可理解为在特定的时间内,占据一定空间的、自然的或人为的同种个体群[2].类似于自然界的种群,面对同一泛顾客群(这里指同一产品大类所面对的顾客群)并存在着相互竞争关系的企业所提供的产品集合之间具有相互替代、交叉衍生的互动关系.因此,可以用生态种群模型来研究产品族谱稳定性,并将产品族谱称为产品种群(见表1).

表1　生物种群和产品种群特征比较Table 1 Comparison of characteristics of biological population and product population

近年来,生态学在不同的领域里受到格外重视与广泛应用,而在产品管理应用方面大多数文献集中于企业产品族规模和结构优化方面,也有少量作者考虑了产品的演化影响因素.Rober[3]指出消费者偏好的差异程度、产品开发的成本和产品的边际收益,是企业确定产品线宽度和长度的主要因素.Fruchter等[4]引入遗传算法探讨产品项之间的蚕食现象,对相关条件下的产品线优化进行了求解.刘伟等[5]以产品族利润最大化为目标,构建了基于消费者选择和成本作用的产品族规模优化模型.此外,有学者利用生态种群竞争理论在解决动态竞争方面的优势尝试研究产品种群竞争,借以完成产品族规模和结构优化.Ommering[6]为了解决软件产品开发过程的多样性和通用性问题提出了产品种群的概念,通过软件架构和模块重组和拆分迅速完成软件产品升级和进化.Kazuhiko等[7]以日本空调数量对气候变暖影响为例,综合生命周期评价和种群平衡模型来评价产品种群的社会规模对环境的影响.Kim等[8]利用考虑了生命周期的种群平衡模型来评估韩国电子和电子设备的浪费情况,取得了较好的效果.何斌等[9]提出了一种基于产品生态学的概念设计框架,在分析了产品基因、产品细胞、产品器官、产品生物体、产品种群和产品群落模型的基础上,提出了产品生态学模型,探讨了产品种群之间的竞争和演化问题.白让让[10]基于泊松模型的实证检验探讨了细分市场间产品线水平延伸的因素分析.李春燕[11]借鉴生物种群之间的Lotka-Volterra竞争模型和理论,将其扩展到用于多种群之间的竞争分析,对不同厂家的创新产品在市场扩散时的竞争演化关系进行研究.陈瑜等[12]借鉴产业生态学的理念,通过引入生态学中Lotka-Volterra竞争捕食者模型,模拟研究了中国光伏产业生态系统的演化路径.牛学杰等[13]基于组织生态理论,重点研究了生态化技术创新与制造业可持续发展之间的关系,并通过建立生态学数理模型进一步分析了生态化技术创新对制造业生态容量的扩大作用.

当前大部分文献将生态种群理论和方法用于研究企业种群和产业种群间协同演化,但其应用尚停留在宏观和中观层面,而深入到企业的微观层面——产品(商品)的文献仍然很少.文献[14]借助组织生态学理论提出产品种群的概念,研究两个存在相互竞争关系的产品在线定制服务提供商的产品种群竞争演化过程,然后利用两个种群互相竞争关系的数学模型模拟产品种群的竞争过程,讨论双方提供的产品种群规模达到均衡时的稳定条件及其经济解.但是,对于企业如何达到这种平衡以及平衡后如何保持这种平衡没有做详尽的阐述,对企业应该制定怎样的研发策略也未过多提及.本文基于种群稳定性理论,将企业产品型谱视为产品种群,探求如何确定产品种群的出生率(新产品开发率)和死亡率(老产品淘汰率)以使企业产品种群获得持续活力,通过不断优化产品种群的规模和年龄就够来平衡客户满意度与产品维护难度、复杂性之间的矛盾.

2　产品种群稳定性和结构优化

2.1不合理的产品种群修正模型

为了平衡上述矛盾,企业需要确定合理的产品族规模,可以借鉴文献[15]等确定合适的产品族规模.在很多情况下,企业实际的产品族规模与理想产品族规模会有很大差距,企业需要根据现有各年龄段产品数量,确定产品种群的新开发率和老产品淘汰率在规定的年限内达到理想的产品种群规模.

为此,假设si表示产品种群中第i年龄段产品存活的概率,si＞0,i=1,2,...,m-1,短期内可以假设为常数;bi表示产品种群中第i年龄段产品的衍生率,bi≥0,i=1,2,...,m,且bi不全为零,其主要取决于企业的研发策略,短期内可以假设为常数;N(k)表示第k年各年龄段产品的数量;Ni(k)表示第k年第i年龄段产品的数量.记ni(k)为第i个年龄段第k时段的种群数量,则n(k)可以表示为

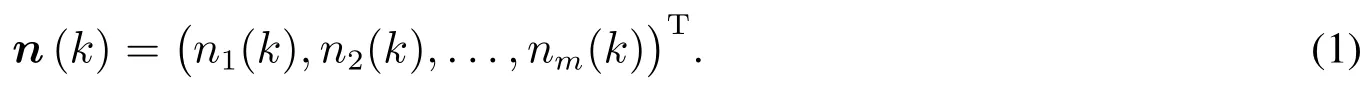
根据以上假设可得

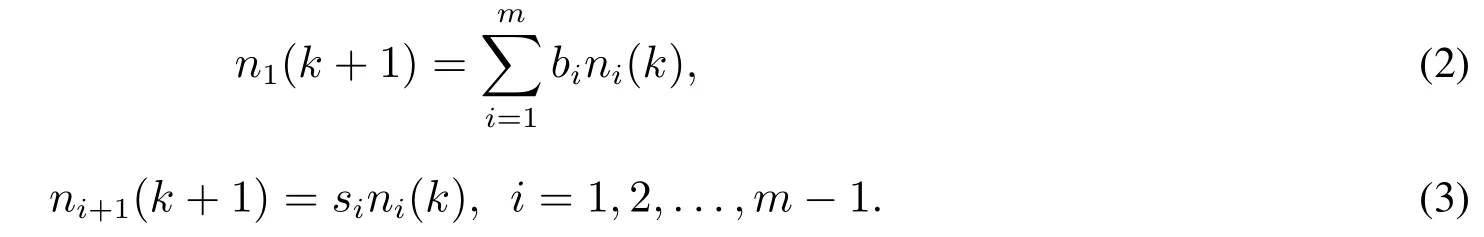
将式(2),式(3)改写成如下矩阵形式

矩阵L有如下性质:矩阵L的正特征根是单重的且唯一,记为λ0.该特征根对应的一个特征向量为

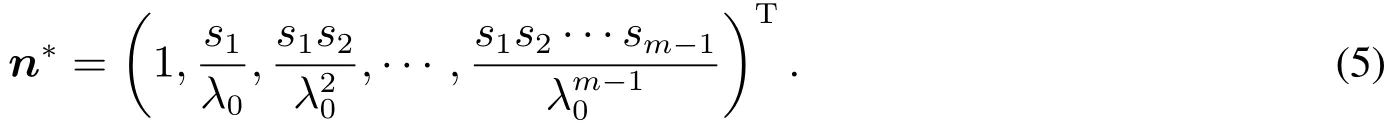
若λ1是矩阵L的任意一个特征根,则必有|λ1|≤λ0.

若L第一行中至少有两个顺次的元素bi,bi+1＞ 0,则|λ1|＜ λ0,,其中c是与n(0)有关的常数.

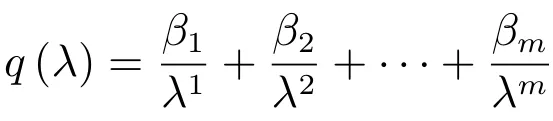
随着产品种群数量的增长,由于受顾客资源,技术储备和产品管理成本等自然资源的制约,产品种群的数量不能无限制的增长,为了平衡满足顾客个性化需求与产品维护难度和成本之间的矛盾,企业会选择不断优化产品结构而产品种群数量稳定在一个常数.

2.2最优种群规模和年龄结构稳定模型

假设种群的最大规模为N,在产品种群接近数量上限时,种群之间的竞争会变得越来越激烈从而会改变各年龄段种群的出生率和存活率,为了避免这种竞争,加入了限制矩阵对种群的结构进行修改,以达到持续增长的效果,加入限制以后使数量在上限附近保持稳定并使种群年龄结构保持最优.每次限制后的产品种群数量与上一次限制之后一样.

假设产品种群中第i个年龄组的产品按hi的比例限制,称其为第i组的限制率,得到限制矩阵H= diag(h1,h2,...,hm),则各组产品限制量可用向量HLn(k)表示,根据持续限制策略的要求得到方程Ln(k)-HLn(k)=n(k),n(k)是矩阵L-HL的特征值为1所对应的特征向量,易得

种群结构稳定的条件为

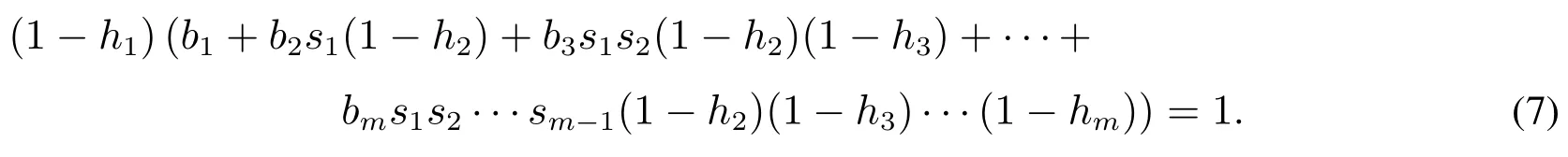
如果h1,h2,···,hm满足式(7)就能保证产品种群的结构稳定,此时对应的一个特征向量为

作为企业,最关心的是在现有不同年龄段的产品种群下,制定怎样的产品研发策略,使得产品种群数量逐渐接近最大值.下面考虑在任给的一个初始年龄向量n∗=(n1(0),n2(0),...,nm(0))T后,怎样确定hi才能保持产品种群数量持续稳定增加.根据式(8),令cn∗=n(0),解得

因此可得

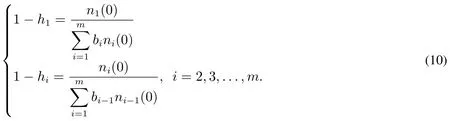
一个理性的企业会不断调整其产品种群的年龄结构来不断满足客户的需求,企业为了平衡客户满意度与产品维护成本、维护难度之间的矛盾,保持产品种群的竞争活力,企业通常会根据产品种群的初始年龄结构,大幅淘汰老旧产品,通过控制产品出生率和淘汰率来保持产品种群的结构稳定,从而在行业保持持续的竞争能力.

企业每年淘汰的老旧产品个数为

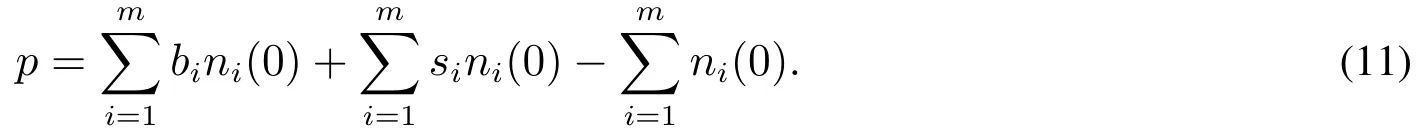
企业在最大可能持续淘汰老旧产品的同时,通过控制出生率和存活率来优化产品种群可以最终归结为下列线性规划问题

种群在满足式(11)和式(12)时会选出一组与任意给定的初态数量相适应的出身率和存活率,企业可以通过调节投入力度来实现.种群会在最优的出身率和存活率下达到最优状态.每个阶段在激烈的竞争下企业都会根据上一年的末态量调整投入力度来保持产品以最适应的出身率和存活率长期维持稳态的生长.其稳态是种群的总量在竞争中会和前一年基本保持一致并且最大限度的接近环境的容纳量.种群能够在保持自身的竞争能力下最大限度的利用资源.

3　算例分析

3.1不合理的产品种群修正案例

企业受到资源、环境和能力的限制确定市场能接受的最大的产品种群数量为1 000个.为了简化起见,将产品种群分为投入期、成长期和成熟期三个年龄阶段(研究衰退期意义不大,因为所有的成熟期的产品都会进入衰退期,企业更关心的是在这三个时期的研发策略),各阶段的初始值n(0)=(429,257,71)T.根据企业统计数据投入期到成长期的产品存活概率为0.5,成长期到成熟期的产品存活概率为0.3.企业计划在5年时间内达到市场容量上限1 000个产品,为此企业要制定不同时期的新产品出生率.

由条件可得出产品的生长矩阵

生长矩阵的唯一正特征值

产品在生长过程中会以唯一正特征值的倍数稳定增长.为满足企业在五年内达到市场容量上限特征值需要满足以下条件,即757λ5≤1 000.

解得λ=1.054 0,在计划5年内达到市场最大值时,产品的投入量每年以1.054倍的比例增张,到达市场上限时的各阶段产品数量分别为558,335,92.总量为986,达到了市场上限的98.6%.

同时根据式(14)以0.01为步长借助搜索法可以解得满足条件的各阶段产品出生率.如表2和图1所示.

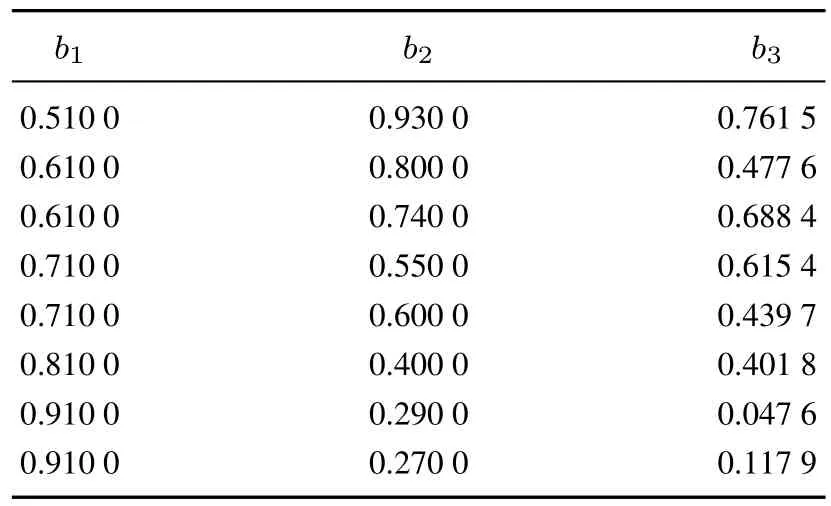
表2　符合条件的部分出生率的值Table 2 The partial birth rate value of meeting the conditions

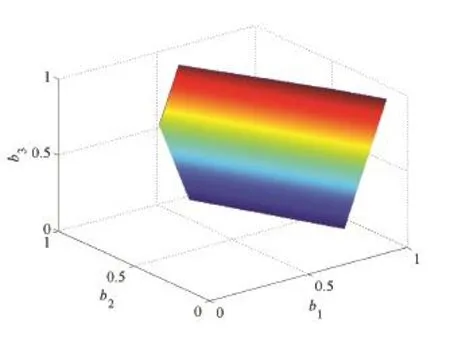
图1　出生率所构成的三维曲面Fig.1 The 3D surface of birth rate

由于满足特征值为1.054的各阶段出生率组成的是一个单位立方体内的一个解曲面,各阶段的取值有很多选择,这也使得企业可根据自身的条件和资源限制灵活的计划投入力度以满足计划需求.

3.2最优种群规模和年龄结构平衡案例

通过算例3.1的优化后,产品种群规模已经达到最优状态n(0)=(558,335,92)T.保持竞争力是每个企业长期生存下去的动力.为了能够持续的占领市场企业需要在已经达到市场上线的产品进行优胜劣汰.它会根据上一年各个阶段产品的销售量来确定本年度在各个阶段的投入力度.根据企业统计数据此时投入期到成长期的产品存活概率为0.61,成长期到成熟期的产品存活概率为0.28.合适的优胜劣汰法则需要满足以下条件:1)各阶段的新产品投入量之和不能小于上一年的第一阶段量;2)各阶段产品的存活量不能小于上一年的下一阶段3)产品的总量不能超过市场上线.通过借助MATLAB软件可解得符合条件的bi,hi.其中bi和hi的部分解(维持稳定的可行解集合)如表3所示

表3　bi和hi的部分解Table 3 The partial solutions of biand hi

表3表示的是在满足产品结构稳定的条件下,企业根据每年的初始态下各阶段的数量应该选择的投入力度和淘汰率,使得产品总量一直维持在不低于98.6%的高市场占有率的稳定趋势.为了更直观的分析企业的投入力度,将出生率隔离开进行分析,用双三次样条插值做出了bi的三维曲面图.如图2所示.

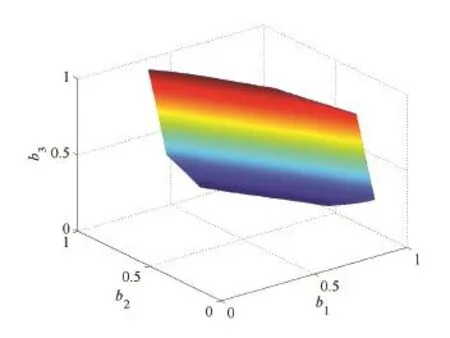
图2　bi的三维取值图Fig.2 Three dimensional value map of bi

企业同样可以根据自身条件限制来计划投入力度对产品进行适当的筛选和培育使得产品在激烈的市场竞争下能长期保持市场占有率.这也给了企业更多选择的余地,使得制定产品计划有更大的灵活度.

4　生长矩阵的参数灵敏度分析

令L=(li,j)n×n;Fj=l1,j,j=1,2,...,n和Pj=lj+1,j,j=1,2,...,n-1分别表示第j年龄组的出生率和存活率.该种群的发展趋势被唯一的最大主特征值λ确定.因此,为了确定种群的未来,只需考察λ.λ是一个重要的参数.另一方面λ由Fi和Pi决定的.Fi和Pi的变化自然会影响λ的取值,进而种群的发展趋势.

设个体的平均生育率R=F1+P1F2+···+P1P2+···+Pn-1Fn.参数的灵敏性判别法则如下:

R＜1时,Pi灵敏的条件是F1+P1F2+···+P1P2+···+Pn-1Fn≥1;

R＞1时,Pi灵敏的条件是F1+P1F2+···+P1P2+···+Pn-1Fn＜1;

Pi灵敏的生物学意义为,R＞1时,Pi灵敏的条件可以理解为,如果种群仅由i岁以下的个体组成,那么种群一定灭亡.只有把超过i岁的个体也添加到种群中时种群才能成为上升的种群.同理可对R＜1的灵敏性进行分析[16].

案例中R=F1+P1F2+···+P1P2F3=b1+0.5b2+0.15b3,代入满足模型条件的出生率可以得到R的一系列取值.为了表示简便,令M=F1,N=F1+P1F2部分计算值如表4所示.

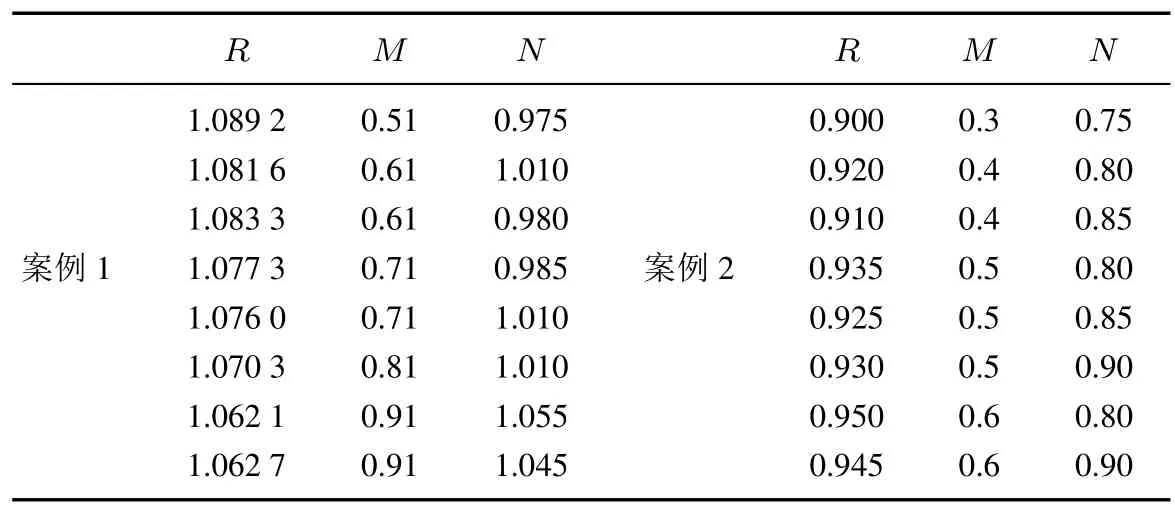
表4　案例1和案例2的计算结果Table 4 The computed results of case 1 and case 2

由案例1可知R＞1,M ＜1则种群只包含一个年龄是不可长期生长下去的.但部分N＞1即通过选取合适的投入力度可以让只含有两个生长阶段的种群保持稳定生长.对于本案例的三个阶段种群来说F1+P1F2+···+P1P2F3＞1即生长矩阵不灵敏,三个阶段的种群是可以保证长期按照主特征值λ的倍数稳定生长.

由案例2可知R＜1,M＜1,N＜1即生长矩阵不灵敏.即使种群中只有一个年龄段或两个年龄段均可保证种群长期按照主特征值λ的倍数稳定生长.

通过以上分析可知三个生长阶段的种群模型是稳定的.企业可以按照模型的求解和自身情况合理的设计研发力度方案来获得持续的市场竞争力并且方案的设计具备灵活性.

5　结束语

本文基于种群稳定性理论,将企业产品型谱视为产品种群,探求如何确定产品种群的出生率(新产品开发率)和死亡率(老产品淘汰率)以使企业产品种群获得持续活力.首先,建立了不合理的产品种群修正模型,通过产品内部演化的动力学原理,揭示了产品最终在稳定水平的状态,其状态是每一年的产品总量不会低于前一年并且能长期的保证高市场占有率以获得持续的市场竞争力,而且能够给企业更多的选择去设计投入力度方案;然后,建立了最优种群规模和年龄结构平衡模型,通过控制出生率和存活率来优化产品种群结构,利用线性规划方法最终使产品种群结构稳定在最优状态,模型给出了一系列的最优出生率和存活率,企业可根据自身的实际情况灵活的选择产品设计方案.最后对模型的参数进行了灵敏性分析以检验模型的鲁棒性,计算出检验数据并与检验条件做了比对,结果表明模型是不灵敏的,即初始量的变动只会对生长矩阵的主特征值产生很微小的变动.模型具备抗扰性.经过上述方法不断优化产品种群的规模和年龄,就能够来平衡客户满意度与产品维护难度、复杂性之间的矛盾.然而,在实践中无论是在产品种群数量上,还是产品年龄结构上,其复杂性远远超过本文所设定的情形;因此,本文仅限于理论与方法的探讨,实际应用中还需要大量的扩充,其计算复杂性也将显著增加.

[1]Wedel M,Kamakura W.Market Segmentation:Conceptual and Met Homological Foundations.Boston:Kluwer Academic Publisher, 2000:29–71.

[2]史刚荣.种群:一个值得重视的生物层次.生物学教学,2001,26(10):29–30. Shi G R.Population:An important biological levels.Mathematical Biology,2001,26(10):29–30.(in Chinese)

[3]Rober B.Determing the approproate depth and breadth of a firm’s product portfolio.Journal of Marketing Research,2003,40(2): 39–53

[4]Fruchter G,Fligler A,Winer R S.Optimal product line design:Genetic algorithm approach to mitigate cannibalization.Journal of Optimization Theory and Applications,2006,131(2):227–244.

[5]刘伟,罗纯军,张子建.基于消费者选择和成本作用的产品族规模优化.系统工程学报,2012,27(5):600–606. Liu W,Luo C J,Zhang Z J.Product family scale optimization model based on interaction of consumer choice and production cost. Journal of Systems Engineering,2012,27(5):600–606.(in Chinese)

[6]Ommering R V.Beyond product families:Building a product population.Lecture Notes in Computer Science,2000,1951:187–198.

[7]Kazuhiko Y,Yasunari M,Masaru Y.Integration of life cycle assessment and population balance model for assessing environmental impacts of product population in social scale case studies for the global warming potential of air conditioners in Japan.The International Journal of Life Cycle Assessment,2003,8(3):129–136.

[8]Kim S,Oguchi M,Yoshida A.Estimating the amount of WEEE generated in South Korea by using the population balance model. Waste Management,2013,33(2):474–483.

[9]何斌,冯培恩,潘双夏.基于产品生态学的概念设计研究.计算机集成制造系统,2007,13(7):1249–1254. He B,Feng P E,Pan S X.Conceptual design based on product ecological model.Journal of Industrial Engineering and Engineering Management,2007,13(7):1249–1254.(in Chinese)

[10]白让让.细分市场间产品线水平延伸的因素分析——基于泊松模型的实证检验.管理评论,2009,21(12):64–70. Bai R R.Analysis on factors affecting inter-segment product line horizontal extension:An empirical test based on Poisson model. Management Review,2009,21(12):64–70.(in Chinese)

[11]李春燕.基于生物种群理论的中国移动通信市场实证研究.管理科学,2009,22(4):56–62. Li C Y.Empirical study on the analysis of Chinese mobile telecommunication market based on biological species theory.Journal of Management Science,2009,22(4):56–62.(in Chinese)

[12]陈瑜,谢富纪.基于Lotka-Volterra模型的光伏产业生态创新系统演化路径的仿生学研究.研究与发展管理,2012,24(3): 74–83. Chen Y,Xie F J.The bionics research of evolutionary path of photovoltaic industry’s innovation ecosystem based on Lotka-Volterra model.R&D Management,2012,24(3):74–83.(in Chinese)

[13]牛学杰,李常洪.生态化技术创新与制造业可持续发展的关系研究.科学技术哲学研究,2013,30(2):105–108. Niu X J,Li C H.Research on the relation between ecological technology innovation.Studies in Philosophy of Science and Technology,2013,30(2):105–108.(in Chinese)

[14]伊辉勇,刘伟.基于产品种群竞争模型的企业核心竞争力识别.管理科学,2007,20(3):16–22. Yi H Y,Liu W.Identifying the core competitive power of company based on the model of product population competition.Journal of Management Science,2007,20(3):16–22.(in Chinese)

[15]伊辉勇,刘伟.行业竞争力导向的在线大规模定制产品族规模优化方法.管理工程学报,2011,23(5):100–105. Yi H Y,Liu W.Size optimization method for on-line mass customization of product family.Journal of Industrial Engineering and Engineering Management,2011,23(5):100–105.(in Chinese)

[16]Paul C,Vogt A.Mathematical analysis of the asymptotic behavior of the Leslie population matrix model.Mathematics Mathematical Biology in General,1973,35(5/6):645–661.

Optimization model for enterprise product population size stability and age structure

Yi Huiyong,Ling Yantao
(College of Business Administration,Chongqing University of Science and Technology,Chongqing 401331,China)

For the same customer groups,product spectrums are mutual substitutes for and derivatives from each other for competitive enterprises.This paper treats the enterprise products pectrum as product population, and explores how to determine the product population’s birth rate(the rate of new product development)and mortality(the elimination rate of old products)in order to enable enterprises to obtain sustainable product population activity.First,a modified model about abnormal product population is set up through the evolutionary dynamics of internal products to reveal the products’stable conditions and the final state.The number of the phase-out products is regarded as the optimization target.The optimal population size and age structure balance model are presented.Linear programming is used to control the birth rate and the survival rate,and then the product population structure is optimized in order to keep the product structure in an optimal state.Finally,an simulation verified the feasibility and effectiveness of the model.

product maintenance complexity;product population;population size;age structure;linear programming

F272.3

A

1000-5781(2016)05-0575-09

10.13383/j.cnki.jse.2016.05.001

2013-09-22;

2014-11-27.

国家自然科学基金资助项目(71102144);重庆市自然科学基金资助项目(cstc2013jcyjA60003).

伊辉勇(1977—),男,辽宁盖州人,博士,教授,研究方向:网络营销,在线大规模定制,Email:yihuiyong1977@126.com;

凌艳涛(1990—),男,河南固始人,硕士生,研究方向:金融数学,数量经济学,Email:1334873728@qq.com.