平直节理黏结颗粒材料宏细观参数关系及细观参数的标定

陈鹏宇,余宏明

(1. 内江师范学院 地理与资源科学学院，四川 内江 641100；2. 中国地质大学(武汉) 工程学院，武汉 430074)



平直节理黏结颗粒材料宏细观参数关系及细观参数的标定

陈鹏宇1,余宏明2

(1. 内江师范学院 地理与资源科学学院，四川 内江 641100；2. 中国地质大学(武汉) 工程学院，武汉 430074)

为了分析平直节理黏结颗粒材料宏细观参数关系以及进行细观参数的标定，以单轴压缩、直接拉伸和双轴压缩数值试验作为宏观参数测试方法，对平直节理接触模型细观参数进行正交设计，采用多因素方差分析和回归分析研究宏细观参数之间的关系，在此基础上，建立了细观参数的标定方法。以灰岩的室内试验为基础，对其细观参数进行标定，模拟结果与试验结果相接近，验证了方法的有效性。

颗粒流；平直节理接触模型；岩石；宏观参数；细观参数

二维颗粒流模型由一系列的圆形颗粒组成，通过它们之间的相互作用来模拟材料的宏观力学性质。为了正确反映岩石的宏观性质，需要选择合理的接触本构模型及其细观参数。最初，颗粒接触黏结模型中只有接触黏结模型和平行黏结模型两种[1]，但是在实际应用中发现这两种模型所得出的单轴抗压强度和单轴抗拉强度比值(UCS/TS)为3～4，低于许多岩石的UCS/TS(一般超过10)[2]。为此，Cho等[3]提出了簇平行黏结模型，该模型将多个黏结颗粒聚集成簇，簇中单个颗粒的旋转被抑制，使得UCS/TS值显著增大。Potyondy[4]则提出了一种适用于硬质岩石的平直节理颗粒黏结模型，将圆形颗粒构造成多边形颗粒，颗粒破坏后的旋转被抑制，使得UCS/TS值显著增大。为此，本文选用平直节理接触模型作为模拟岩石的颗粒接触本构模型。

在颗粒流数值模拟中，细观参数的标定是最重要的准备工作之一，其关系到是否能够正确模拟材料的宏观力学性质。目前，多通过研究黏结颗粒材料宏细观参数之间的关系来实现细观参数的标定。Yoon等[5]研究了接触黏结颗粒材料宏细观参数的关系。颜敬等[6]研究了无黏结颗粒材料宏细观参数的关系。周喻等[7]、越国彦等[8]、曾青冬等[9]、丛宇等[10]研究了平行黏结颗粒材料中细观参数对宏观特性的影响。夏明等[2]研究了簇平行黏结颗粒材料中细观参数对宏观参数的影响。这些研究都为细观参数的标定提供了依据，但其研究成果均未涉及平直节理接触模型。为此，笔者以平直节理黏结颗粒材料为研究对象，通过正交试验设计、多因素方差分析和回归分析研究其宏细观参数之间的关系，并建立细观参数的标定方法。

1 二维颗粒流基本理论

1.1 平直节理接触模型

二维颗粒流模型中平直节理接触模型能够抑制黏结破坏后颗粒的旋转，这是与接触黏结模型和平行黏结模型的最大区别。典型的平直节理接触模型如图1所示。

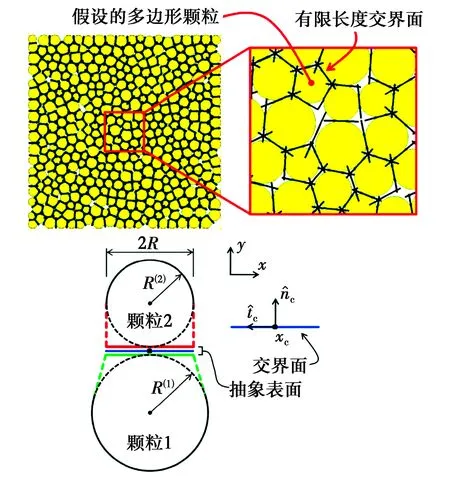
图1 平直节理接触模型[4]Fig.1 Flat-jointed contact

平直节理接触模型有未黏结和黏结两种模式，两者的本构关系不同。对于未黏结部分，剪切强度为

(1)

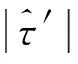
对于黏结部分，剪切强度为

(2)

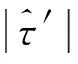
1.2 岩石数值试验

(3)

(4)

(5)

式中：P为垂直荷载，N；A为试样横截面面积，mm2；σ为压应力值,MPa；E为变形模量；v为泊松比；σ50为单轴抗压强度50%的应力值；εl50为σ50对应的垂直应变；εd50为σ50对应的横向应变。

另一个确定细观参数的重要数值试验就是直接拉伸数值试验，用于测试试样的抗拉强度(图3)，数值试样破裂时的峰值强度即为抗拉强度σt。

图2 单轴压缩数值试验Fig.2 Uniaxial compression numerical

图3 直接拉伸数值试验Fig.3 Direct tension numerical

除了直接拉伸数值试验以外，也可以通过间接拉伸(巴西劈裂)数值试验，如图4所示。根据数值试样破裂时的峰值作用力Ff，可得数值试样的抗拉强度，计算公式见式(6)。

(6)

式中：σt为试样抗拉强度；P为试样破坏荷载；D为试样直径；L为试样高度。

由于巴西劈裂和直接拉伸所测的抗拉强度之间存在较大差异，为了获得准确的抗拉强度，数值试验时采用直接拉伸测定抗拉强度。

图4 间接拉伸(巴西劈裂)数值试验Fig.4 Indirect tensile (brazil disk split) numerical

图5 双轴压缩数值试验Fig.5 Biaxial compression numerical

2 宏细观参数之间的关系

颗粒流模型由颗粒组成，模型的宏观参数是由颗粒和黏结的细观参数决定，两者之间具有相关性。目前多采用试错法确定细观参数，即对比室内试验和数值试验的结果，通过不断调节细观参数，以达到可接受的精度范围。也有研究通过回归分析[5]和BP神经网络模型[7]反演细观参数，但都是针对比较简单的接触黏结模型和平行黏结模型，需要确定的细观参数较少。本文的研究对象为平直节理接触模型，其主要细观参数包括：N、Ec、kn/ks、μb、λ、σb、cb、φb。其中：N为交界面段数；Ec为平直节理模量；kn/ks为平直节理刚度比；μb为平直节理摩擦系数；λ为平直节理两端较小颗粒的半径比；σb为平直节理抗拉强度；cb为平直节理粘聚力；φb为平直节理内摩擦角。

平直节理接触模型细观参数较多，如果盲目地调节细观参数，有可能导致大量数值试验，增加建模的难度。为此，可通过研究平直节理黏结颗粒材料宏细观参数之间的关系，为细观参数的标定提供依据，从而降低试错法数值试验的数量，更快捷的确定细观参数。

2.1 正交试验设计

正交试验设计根据正交性从全面试验中挑选出部分有代表性的点进行试验，可以在很大程度上减少数值试验的数量[12]。在进行正交试验设计之前，考虑到平直节理黏结颗粒材料细观参数较多，增加了数值试验的数量和细观参数标定的难度，有必要进行一定的假设，以减少细观参数的数量。参考Potyondy[4]、Poulsenn等[13]的研究，作以下假设：

1)平直节理抗拉强度小于抗剪强度，即σb<τb=cb+σtanφb(可获得符合实际的岩石拉压强度比)；

2) 平直节理两端较小颗粒的半径比λ = 1；

3)取最小粒径Rmin= 0.5mm，颗粒半径比固定为1.66；

4)平直节理交界面段数N=4；

5)颗粒密度取2 700kg/m3；

6)颗粒接触模量、刚度比和摩擦系数同平直节理一致。

由此，根据所需确定的细观参数建立正交试验设计表(表1)，设计的正交矩阵序列如表2所示。分别进行单轴压缩、直接拉伸和双轴压缩数值试验(试样宽50mm，高100mm)，加载速率0.01m/s。由此得到宏观参数：变形模量E、泊松比v、单轴抗压强度σf、抗拉强度σt、内摩擦系数tanφ和内聚力C。这样细观参数和宏观参数都是6个，降低了细观参数标定的不确定性。数值试验所得结果如表3所示，符合大部分岩石的宏观参数取值范围。

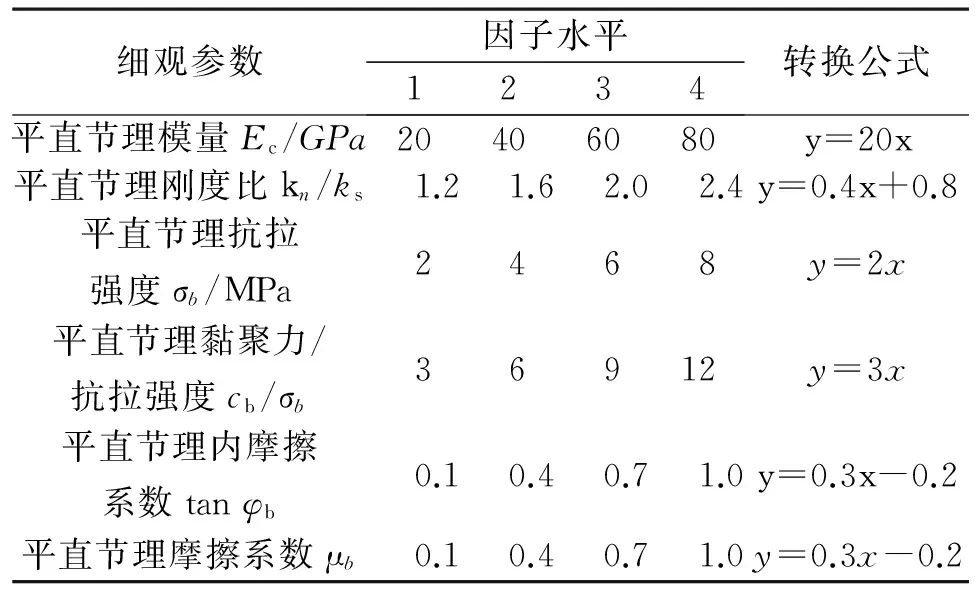
表1 平直节理接触模型细观参数正交试验设计表Table 1 Orthogonal test design table of microparametersfor flat-jointed contact model

表2 平直节理接触模型正交设计矩阵序列Table 2 Orthogonal matrix sequence of microparameters for flat-jointed contact model

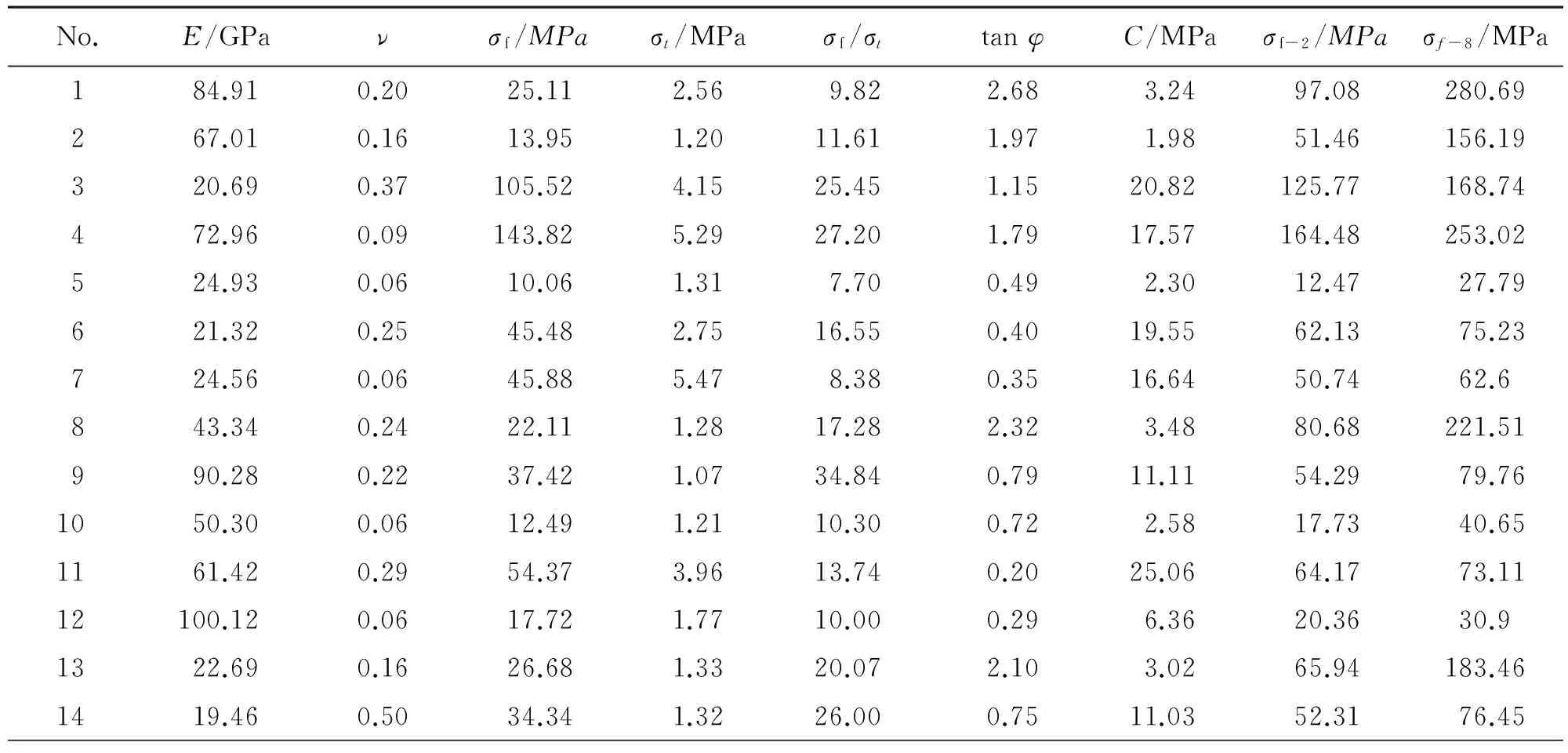
表3 正交设计矩阵序列对应的宏观参数计算结果Table 3 Calculated results of macroparameters corresponding to orthogonal matrix sequence

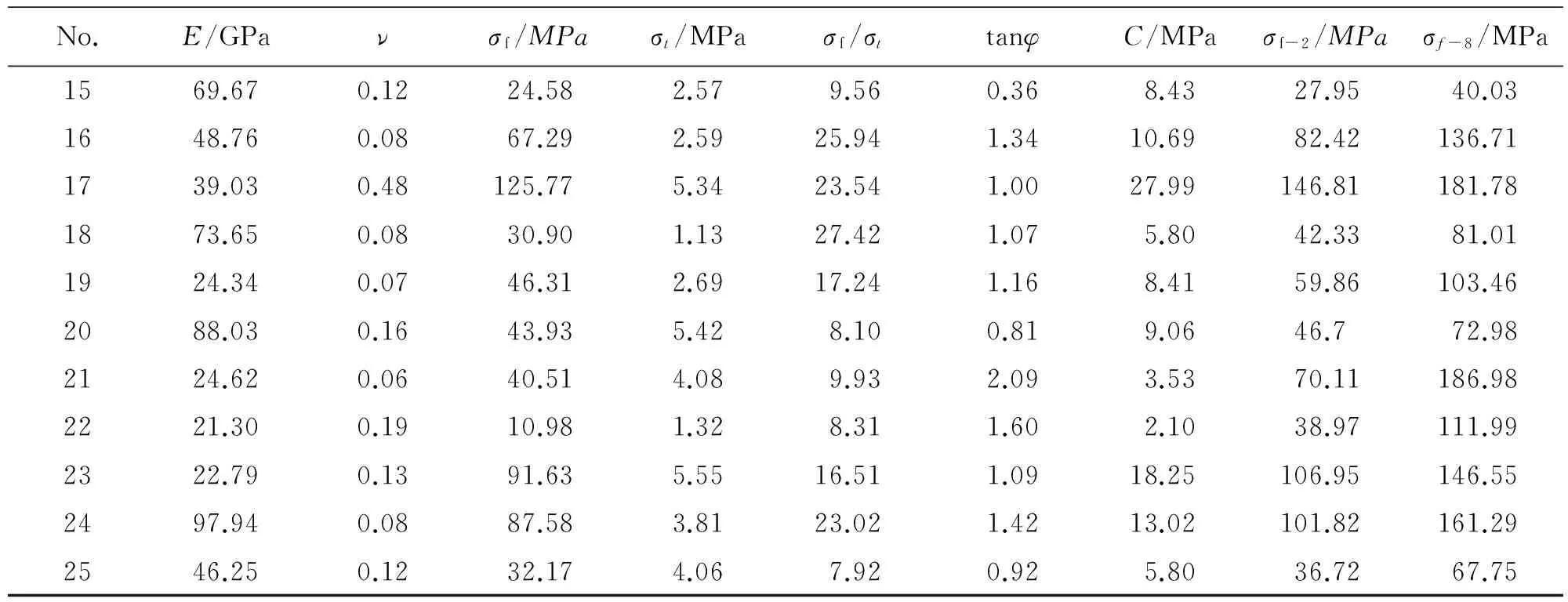
续表3

2.2 多因素方差分析

多因素方差分析是用于研究多个因素对一个因变量是否具有显著影响的统计分析方法，即研究多个因素的不同水平以及各因素之间的相互作用对实验结果的影响[14]。本文中考虑各因素的主效应，取检验的显著性水平为α= 0.05，如果Sig. ≤α，则认为对应因素对因变量产生显著影响，如果Sig. >α，则认为对应因素对因变量没有产生显著影响。

在进行多因素方差分析时，σb、cb/σb和cb三者之间不具有相对独立性，任意一个参数都能被其余两个表示，因此，只能选择cb/σb和cb其中一个进行分析。经过分析发现，宏观参数中的v和σf/σt与cb/σb具有密切的关系，在这两个宏观参数作为因变量时，采用cb/σb进行多因素方差分析，其余宏观参数采用cb进行多因素方差分析。

根据多因素方差分析的F统计量和相伴概率值Sig.的结果可得宏观参数的显著性影响因素及其排序结果为变形模量E：Ec>kn/ks>σb

泊松比v：kn/ks>cb/σb>μb>Ec>tanφb

单轴抗压强度σf：cb>σb>tanφb

抗拉强度σt：σb

内摩擦系数tanφ：μb>tanφb

内聚力C：cb> μb>kn/ ks>σb

压拉强度比σf/σt：cb/σb>tanφb

围压2 MPa下的双轴抗压强度σf-2：cb> μb> tanφb> kn/ks

围压8MPa下的双轴抗压强度σf-8：μb> cb> tanφb>kn/ks。

图6给出了多因素方差分析的F统计量的结果，其中,X1：Ec，X2：kn/ks，X3：σb，X4：cb/σb(cb)，X5：tanφb，X6：μb。根据图6的结果，可得以下结论：

1)变形模量E主要受到节理模量Ec、节理刚度比kn/ ks和节理抗拉强度σb的影响，其中,节理模量Ec的影响程度远大于其余两者，节理刚度比kn/ ks次之，节理抗拉强度σb最弱，几乎可以忽略。

2)泊松比v受到多种因素的影响，包括节理刚度比kn/ks、节理强度比cb/σb、节理摩擦系数μb、节理模量Ec、节理内摩擦系数tanφb，其中,节理刚度比kn/ ks和节理强度比cb/ σb影响程度相对较大，其余细观参数影响程度相差不大。

3)单轴抗压强度σf主要受到节理抗拉强度σb、节理黏聚力cb和节理内摩擦系数tanφb的影响，其中,节理黏聚力cb的影响程度远大于其余两者，其余细观参数影响程度相差不大，这是因为单轴压缩条件下，无围压的影响，使得节理内摩擦系数tanφb发挥的作用相对较小。

4)抗拉强度σt主要受到节理抗拉强度σb的影响，使得该细观参数最易标定。

5)内摩擦系数tanφ主要受到节理摩擦系数μb和节理内摩擦系数tanφb的影响，其中,节理摩擦系数μb的影响程度远大于节理内摩擦系数tanφb。

6)内聚力C受到多种因素的影响，包括节理黏聚力cb、节理摩擦系数μb、节理刚度比kn/ ks和节理抗拉强度σb的影响，其中以节理黏聚力cb和节理摩擦系数μb影响程度相对较大，其余两者次之。

7)压拉强度比σf/σt主要受到节理强度比cb/σb和节理内摩擦系数tanφb，其中,节理强度比cb/ σb的影响程度远大于节理内摩擦系数tanφb。

8)双轴抗压强度σf-2和σf-8主要受到节理摩擦系数μb、节理黏聚力cb、节理内摩擦系数tanφb和节理刚度比kn/ ks的影响。

对比单轴抗压强度σf、双轴抗压强度σf-2和σf-8细观参数的F统计量可以发现，单轴抗压强度σf几乎不受节理摩擦系数μb的影响，而主要受节理黏聚力cb的影响。随着围压增大，节理摩擦系数μb对峰值强度的影响逐渐增大，而节理黏聚力cb对峰值强度的影响逐渐减小。为了验证上述观点，对双轴抗压强度0.5(σf-2+ σf-8)进行多因素方差分析，结果如图6(j)所示，可以发现,节理黏聚力cb和节理摩擦系数μb对峰值强度的影响介于两者之间。

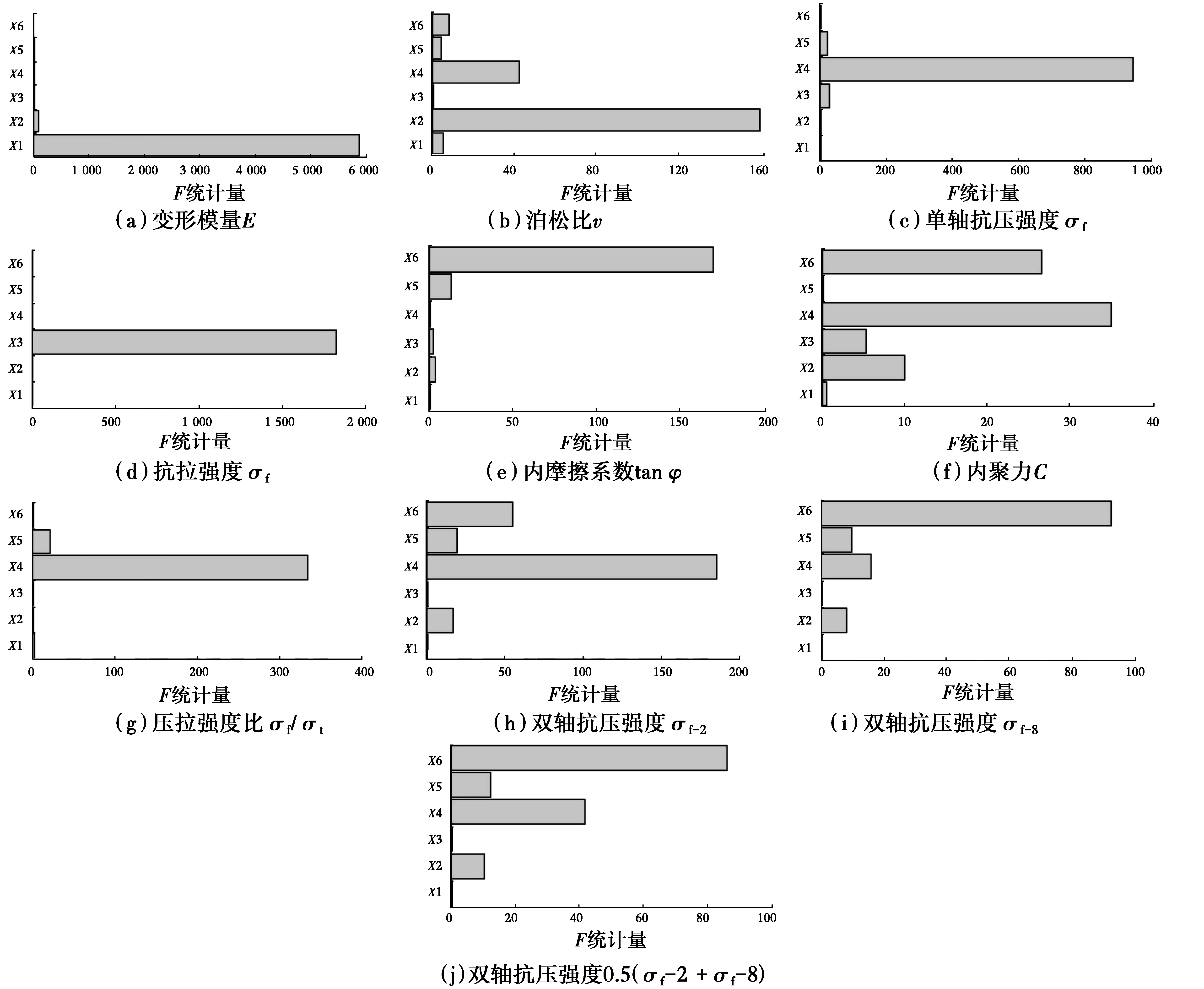
图6 多因素方差分析的F统计量Fig.6 F-statistics of multi-factor analysis of

2.3 回归分析

根据上述正交试验计算结果可以建立宏观参数与其主要显著影响因素之间的关系式。取显著性水平为α= 0.05作为回归系数检验的标准，若某系数的相伴概率值Sig. > 0.05，则在回归分析中去掉对应的细观参数，直到所有回归系数的相伴概率值Sig. ≤ 0.05。所得结果如表4所示，其中，只有变形模量E回归分析中的节理抗拉强度σb未通过系数显著性检验。

从表4中可以看出，宏观参数拟合公式的R2值在0.881～0.996之间，说明拟合效果较好，能够比较准确反映宏细观参数之间的关系，其中,以变形模量E、单轴抗拉强度σf和抗拉强度σt的拟合效果相对较好，相关系数R2大于0.99；而内摩擦系数tanφ和内聚力C的拟合效果相对较差，说明两者与细观参数的关系较为复杂；泊松比回归分析中入选的细观参数最多，说明泊松比受到了多种因素的影响，与细观参数之间的关系也比较复杂。虽然回归分析的拟合效果参差不齐，但是这些公式可以定性地反映宏细观参数之间的关系。对应的回归系数为正，则说明细观参数与宏观参数之间呈正相关关系；对应的回归系数为负，则说明细观参数与宏观参数之间具有负相关关系。

表4 宏观参数与细观参数之间的回归方程式及拟合度Table 4 Regression equations of macroparametersand microparameters and corresponding degree of fitting

2.4 颗粒粒径对宏观性质的影响

上述分析中颗粒最小半径Rmin= 0.5 mm，颗粒半径比固定为1.66，在实际应用中，为了得到更好的模拟效果，我们可能会选择更小的颗粒粒径，这时候就需要考虑颗粒粒径对宏观参数的影响。分别选择颗粒最小粒径为0.50、0.45、0.40、0.35 mm，颗粒半径比固定为1.66进行数值试验，获取宏观参数。平直节理黏结颗粒材料的细观参数选择如表5所示，该细观参数对应的宏观参数满足一般岩石力学性质对应的范围。

图7为宏观参数相对于颗粒最小粒径的变化曲线。从图中可以看出，在细观参数不变的情况下，颗粒粒径的改变对试样宏观强度和变形性质的影响都比较小，仅内摩擦角和内聚力的变化幅度相对较大。上述结果表明，在一定范围内，颗粒流模型宏观性质受粒径改变的影响较小。

表5 平直节理黏结颗粒材料的细观参数Table 5 Microparameters of flat-jointed bonded-particle material

图7 宏观参数相对于颗粒最小粒径的变化曲线Fig.7 Curve of macroparameters vs minimum grain diameter of particles

3 岩石细观参数标定方法

由于宏、细观参数之间具有相关性，同样类似于2.3节中的回归分析，也可以建立细观参数为因变量，宏观参数为自变量的线性回归表达式。这里采用逐步回归法[15]，通过SPSS软件实现，变量进入的概率门槛值为0.05，删除的概率门槛值为0.10，拟合结果见表6。

表6 细观参数与宏观参数之间的回归方程式及拟合度Table 6 Regression equations of microparameters and macroparameters and corresponding degree of fitting

(7)

将表3中的宏观参数σf和tanφ代入式(7)预测C值，并与表3中的C值进行对比，以此说明颗粒流模型是否能够反映岩石宏观参数之间的基本关系。对比结果如图8所示，从中可以看出预测值与实际值之间相关系数达到了0.969 3，拟合关系式中系数1.048 2，非常接近于1，这说明颗粒流模型所反映的岩石宏观参数之间的基本关系是符合实际的。

根据表6中的线性拟合公式，可以初步确定细观参数，至于tanφb可取0.5作为初始值。此时，所确定的细观参数只是初步估计，并不能准确反映宏观性质，还需进行数值试验计算宏观参数，对比计算宏观参数与实际宏观参数之间的差别，再根据表4中拟合公式中所反映的宏细观参数之间的趋势性关系，可对细观参数进行适当微调，直到达到合理的精度范围。如果改变颗粒粒径建立数值模型，则需要重新调整细观参数，由于颗粒粒径变化对岩石宏观性质的影响并不大，可通过数值试验对细观参数进行适当微调。

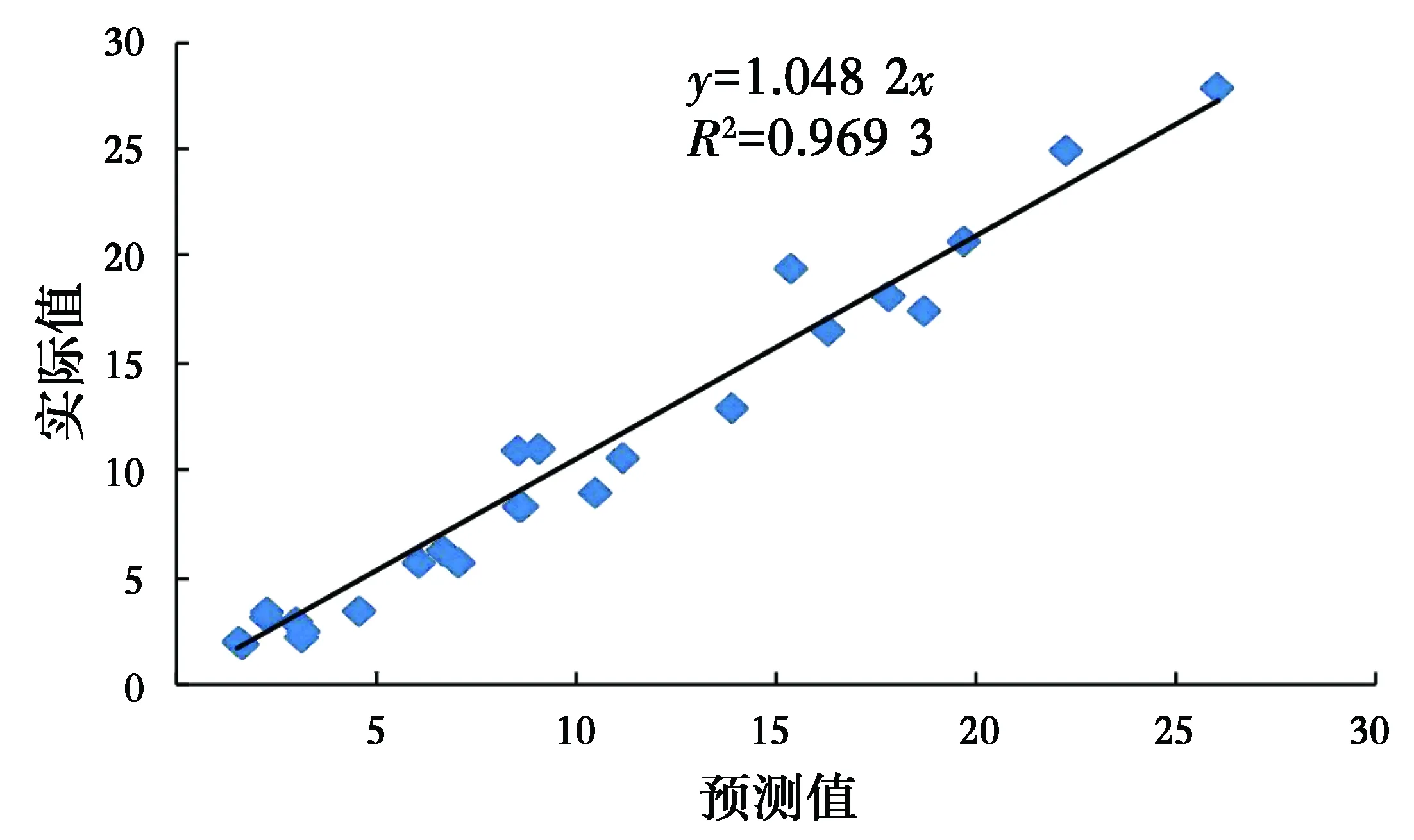
图8 黏聚力C预测值与实际值对比Fig.8 Comparison of actual value and prediction value of

4 实例分析

4.1 细观参数的标定

采用焦作市龙寺废弃矿山奥陶系中统上马家沟组(O2s)厚层状灰岩。每组试样4个，在INSTORN-1346电液伺服岩石力学测试系统进行单轴压缩和巴西劈裂试验，取测试结果平均值，如表7所示。

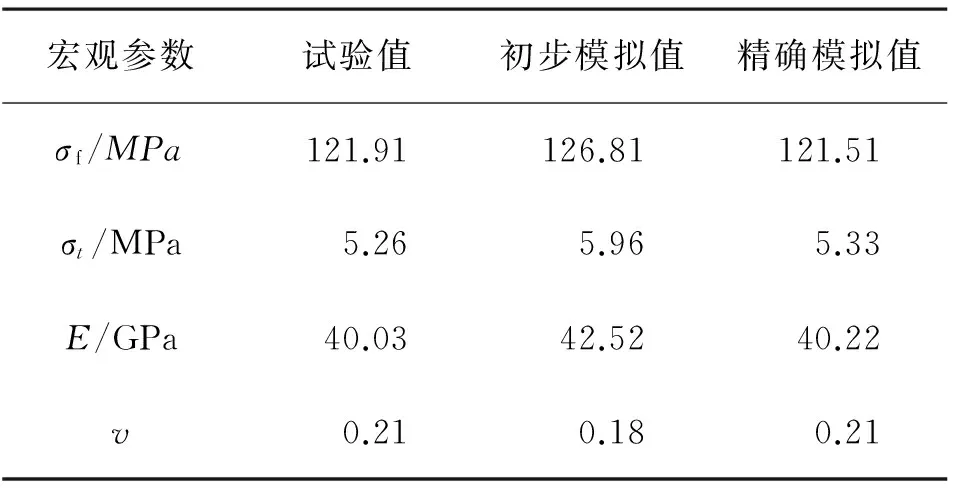
表7 岩石试样宏观参数的试验值和模拟值Table 7 Test and simulated macroscopic parameters of rock sample

由于未测试灰岩三轴强度参数，本文仅标定Ec、kn/ks、σb、cb4个细观参数，tanφb和μb统一取为0.5。在正交试验时，本文采用直接拉伸试验确定抗拉强度，而岩石试验采用巴西劈裂试验。数值模拟结果表明，直接拉伸的抗拉强度一般是平台巴西劈裂抗拉强度的95%左右[11, 17]，对于本文的平直节理黏结颗粒材料，按表2数据经测算该系数平均为92%。因此，将巴西劈裂试验所确定抗拉强度乘以系数92%即可采用表6中公式初步确定细观参数。生成颗粒流试样时，采用的空隙率为0.1，由此可以根据岩石密度确定颗粒密度，采用公式

(8)

式中:ρs为颗粒密度；ρ为岩石密度；r为数值试样空隙率，取0.1。

将表7中宏观参数(抗拉强度乘以系数92%)代入表6中的拟合公式初步确定细观参数如表8所示。根据初步确定的细观参数进行数值试验可得宏观参数的初步模拟值如表7所示，可以看出初步模拟值已经比较接近于实际值。对比初步模拟值与实际值之间的差别，再根据宏细观参数之间的趋势性关系进行微调，最终获得精确估计的细观参数如表8所示。对应的精确模拟值见表7，可以看出精确模拟值已经非常接近于实际值。由此说明本文方法是可行的。

表8 岩石细观参数标定结果Table 8 Calibration results of rock mesoscopic parameters

4.2 数值模拟结果分析

4.2.1 试样破坏对比 破坏试样的对比如图9、图10所示。从图中可以看出，数值模拟结果与岩石试验结果是比较一致的。单轴压缩下岩样的破坏形态都主要表现为脆性劈裂破坏以及表层剥离；巴西劈裂下岩样的破坏形态都主要表现为径向的脆性劈裂破坏。

图9 单轴压缩下岩样破坏形态Fig.9 Rock failure pattern of uniaxial compression

图10 巴西劈裂下岩样破坏形态Fig.10 Rock failure pattern of brazil disk split

图11 应力应变曲线对比Fig.11 Comparison of the stress-strain

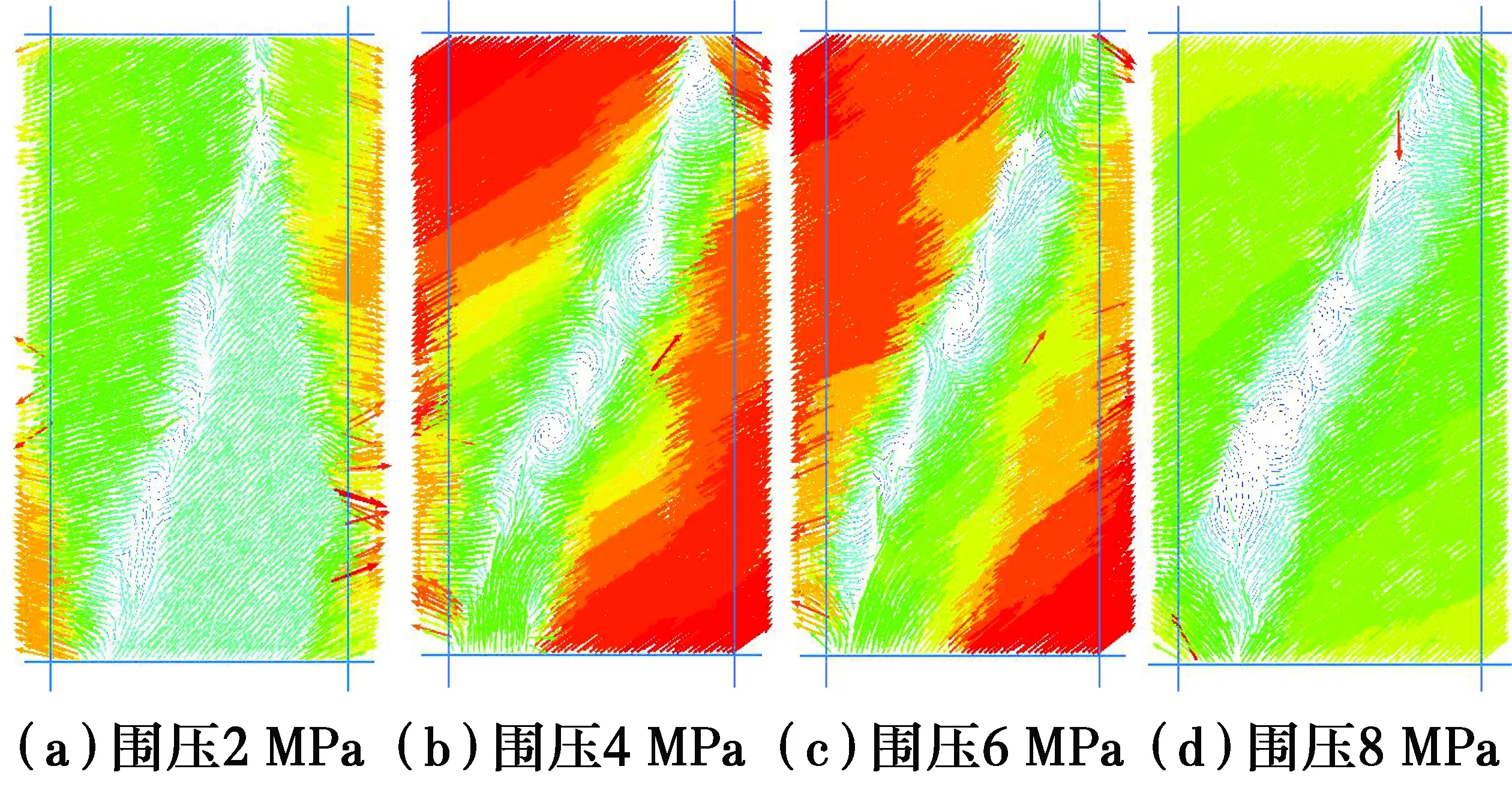
图12 双轴压缩数值模拟结果Fig.12 Numerical simulation result of biaxial compression

5 结 论

1)采用正交试验设计、多因素方差分析和回归分析研究了平直节理黏结颗粒材料宏细观参数之间的关系，确定了宏观参数的显著性影响因素(细观参数)及其排序，确定了宏细观参数之间的相关关系。

2)建立了以细观参数为因变量，宏观参数为自变量的线性回归表达式，由此提出了岩石细观参数的标定方法，即以线性回归表达式初步估计细观参数，然后进行数值试验对比计算宏观参数与实际宏观参数之间的差别，再根据宏细观参数之间的趋势性关系，对细观参数进行适当微调，直到达到合理的精度范围。

[1] POTYONDY D O，CUNDALL P A.A bonded-particle model for rock [J].International Journal of Rock Mechanics and Mining Sciences，2004，41(8)：1329-1364.

[2] 夏明，赵崇斌.簇平行黏结模型中微观参数对宏观参数影响的量纲研究[J].岩石力学与工程学报，2014，33(2)：327-338.

XIA M，ZHAO C B. Dimensional analysis of effects of microscopic parameters on macroscopic parameters for clump parallel-bond model [J].Chinese Journal of Rock Mechanics and Engineering，2014，33(2)：327-338. (in Chinese)

[3] CHO N，MARTIN C D，SEGO D C.A clumped particle model for rock [J].International Journal of Rock Mechanics and Mining Sciences，2007，44(7)：997-1010.

[4] POTYONDY D O.A flat-jointed bonded-particle material for hard rock [C]// Proceedings of the 46th US Rock Mechanics Symposium，Chicago，2012：24-27.

[5] YOON J.Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation [J].International Journal of Rock Mechanics & Mining Sciences，2007，44(6)：871-889.

[6] 颜敬，曾亚武，高睿，等.无黏结材料颗粒流模型的宏细观参数关系研究[J].长江科学院院报，2012，29(5)：45-50.

YAN J，ZENG Y W，GAO R，et al.Relationship between macroscopic and mesoscopic parameters in particle flow model of unbounded material [J].Journal of Yangtze River Scientific Research Institute，2012，29(5)：45-50. (in Chinese)

[7] 周喻，吴顺川，焦建津，等.基于BP神经网络的岩土体细观力学参数研究[J].岩土力学，2011，32(12)：3821-3826.

ZHOU Y，WU S C，JIAO J J，et al.Research on mesomechanical parameters of rock and soil mass based on BP neural network [J].Rock and Soil Mechanics，2011，32(12)：3821-3826. (in Chinese)

[8] 赵国彦，戴兵，马驰.平行黏结模型中细观参数对宏观特性影响研究[J].岩石力学与工程学报，2012，31(7)：1491-1498.

ZHAO G Y，DAI B，MA C.Study of effects of microparameters on macroproperties for parallel bonded model [J].Chinese Journal of Rock Mechanics and Engineering，2012，31(7)：1491-1498. (in Chinese)

[9] 曾青冬，姚军，霍吉东.基于并行 PSO算法的岩石细观力学参数反演研究[J].西安石油大学学报(自然科学版)，2015，30(4)：27-32.

ZENG Q D，YAO J，HUO J D.Inversion of rock meso-mechanical parameters based on parallel particle swarm optimization(PSO) algorithm [J].Journal of Xi'an Shiyou University (Natural Science Edition)，2015，30(4)：27-32. (in Chinese)

[10] 丛宇，王在泉，郑颖人，等.基于颗粒流原理的岩石类材料细观参数的试验研究[J].岩土工程学报，2015，37(6)：1031-1040.

CONG Y，WANG Z Q，ZHENG Y R，et al.Experimental study on microscopic parameters of brittle materials based on particle flow theory [J].Chinese Journal of Geotechnical Engineering，2015，37(6)：1031-1040. (in Chinese)

[11] 孟京京，曹平，张科，等. 基于颗粒流的平台圆盘巴西劈裂和岩石抗拉强度[J]. 中南大学学报(自然科学版)，2013，44(6)：2449-2454.

MENG J J，CAO P，ZHANG K，et al.Brazil split test of flattened disk and rock tensile strength using particle flow code [J]. Journal of Central South University (Science and Technology)，2013，44(6)：2449-2454. (in Chinese)

[12] 张伟，韩旭，刘杰，等.一种基于正交试验设计的土中爆炸数值模型确认方法[J]．工程力学，2013，30(3)：58-65.

ZHANG W，HAN X，LIU J，et al.A method for model validation of underground explosion based on the orthogonal experimental design [J].Engineering Mechanics，2013，30(3)：58-65. (in Chinese)

[13] POULSENN B A，ADHIKARY D P.A numerical study of the scale effect in coal strength [J].International Journal of Rock Mechanics & Mining Sciences，2013，63：62-71.

[14] 谭海中，何波.基于多因素方差分析的文本向量特征挖掘算法[J].科技通报，2015，31(6)：139-141.

TAN H Z，HE B.Algorithm of text vectors feature mining based on multi factor analysis of variance [J].Bulletin of Science and Technology，2015，31(6)：139-141. (in Chinese)

[15] 范雯.逐步回归分析方法在储层参数预测中的应用[J].西安科技大学学报，2014，34(3)：350-355.

FAN W. Application of stepwise regression analysis method in reservoir parameter prediction [J].Journal of Xi’an University of Science and Technology，2014，34(3)：350-355. (in Chinese)

[16] 刘佑荣，唐辉明.岩体力学[M].北京：化学工业出版社，2008.

[17] 王启智，贾学明.平台巴西圆盘试样确定脆性岩石的弹性模量、拉伸强度和断裂韧度—第一部分：解析和数值结果[J].岩石力学与工程学报，2002，21(9)：1285-1289.

WANG Q Z,JIA X M.Determination of elastic modulus，tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen-Part I：Analytical and numerical results [J].Chinese Journal of Rock Mechanics and Engineering，2002，21(9)：1285-1289. (in Chinese)

(编辑 王秀玲)

National Natural Science Foundation of China (No. 41272377)

Relationship between macroparameters and microparameters of flat-jointed bonded-particle material and calibration of microparameters

Chen Pengyu1，Yu Hongming2

(1. School of Geography & Resource Science, Neijiang Normal University, Neijiang 641100, Sichuan, P. R. China;2. Faculty of Engineering, China University of Geosciences, Wuhan 430074, P. R. China)

The orthogonal design and multi-factor analysis of variance is adopted to analyze the relationship between macroparameters and microparameters of flat-jointed bonded-particle material and to establish the calibration method of microparameters. Firstly, the orthogonal design is adopted to conduct the macroparameters of flat-jointed contact model and the uniaxial compression, direct tension and biaxial compression numerical test is used to calculate the macroparameters of rock. Then multi-factor analysis of variance and regression analysis are adopted to analyze the relationship between macroparameters and microparameters. On this basis, calibration method of microparameters for rock is proposed in this paper. Based on laboratory tests of limestone, the microparameters of limestone are calibrated. The simulation results are closed to the laboratory test results, and this validated the significance of the proposed method.

PFC; flat-jointed contact model; rock; macroparameters; microparameters

10.11835/j.issn.1674-4764.2016.05.010

2015-08-07

国家自然科学基金(41272377)

陈鹏宇(1987-)，男，博士，主要从事地质灾害分析评估、预测预报和数值模拟研究，(E-mail)andycoy1@163.com。

TU457

A

1674-4764(2016)05-0074-11

Received:2015-08-07

Author brief：Chen Pengyu (1987- )，PhD，main research interests：analysis, prediction and numerical simulation of geological disaster，( E-mail ) andycoy1@163.com.