基于位置无关名字的可扩展几何路由方案

孙彦斌，张宇，张宏莉，方滨兴

(哈尔滨工业大学计算机科学与技术学院，黑龙江 哈尔滨150001)

研究与开发

基于位置无关名字的可扩展几何路由方案

孙彦斌，张宇，张宏莉，方滨兴

(哈尔滨工业大学计算机科学与技术学院，黑龙江 哈尔滨150001)

名字路由已成为未来网络的研究热点之一，由于网络中节点和信息规模的持续增长，可扩展问题成为其瓶颈。几何路由作为新型可扩展路由方案，可同时满足路由表规模和路由路径的可扩展，但难以支持名字路由。首先在几何路由基础上提出了一种通用的基于位置无关名字的可扩展几何路由方案——GRIN，结合源路由和贪心路由实现混合几何路由，在混合几何路由上引入基于双层稀疏群组的名字解析(映射)。然后理论分析了节点状态及名字映射的路径延展度上界。最后通过仿真验证了GRIN具备可扩展、低延展度以及高可靠性等特征，并优于其他名字路由方案。

几何路由;名字解析;名字路由;可扩展性

1 引言

名字路由采用位置无关(location-independent)的名字(标识)进行寻址，其将标识/位置分离，是解决当前互联网络IP语义过载问题的重要手段，提高网络移动性并消除地址管理分配的负担。同时，互联网正朝着面向内容的方向发展，重新设计互联网体系结构成为未来互联网研究的趋 势 。ICN(information centric networking)［1］采 用 以 内 容 为中心的设计方案，将网络关注的重心由位置(where)转向内容(what)，是Internet最有可能的替代者之一。为实现位置无关的内容寻址，名字路由成为ICN的关键技术。可见，名字路由已成为当前及未来互联网络研究的重点。

名字路由采用标识和位置分离方案，依靠位置无关的名字寻址。本文中，名字具有广义的概念，是任意网络对象(如主机、内容或服务)的身份标识，具备全局性、唯一性和持续性。全局和唯一指不同对象之间名字唯一，且全局可见。持续性是指保证名字不受其所有者、位置、时间等因素影响。

名字路由可分为两类:一类直接根据名字路由，ROFL［2］根据节点ID采用贪心路由实现主机间通信，CCN［3］用名字替代IP地址，采用类似OSPF的路由方案实现内容或服务查询;另一种采用基于名字解析的路由方式，先通过名字解析获得对象的位置信息，再选择合适的位置通信，如LISP［4］、Disco［5］、TRIAD［6］、DONA［7］、NetInf［8］。

无论采用直接路由还是名字解析，名字路由都面临严重可扩展问题:一方面，由于互联网节点和内容数量庞大并持续增长，海量网络对象将产生庞大的位置无关的名字空间，导致路由表规模过大。同时，由于名字的位置无关性，名字相似的网络对象很难来自相邻节点，相同名字的网络对象也可能分布在多个节点，导致名字聚合难以实现。另一方面，名字的位置无关性使得名字不包含位置和路由信息，导致路由效率低下。为解决以上问题，需要设计一种基于位置无关名字的可扩展路由方案。

可扩展的名字路由应满足以下条件:位置无关，采用任意(随机)的名字进行路由，保证名字与位置无关;可扩展(scalability)，保证路由表与网络规模呈亚线性关系，使得存储、计算等资源满足网络规模的增长;低延展度(low stretch)，延展度即节点间实际路径长度与最短路径长度的比值，低延展与可扩展相互矛盾，二者折中是可扩展路由成功的关键;可靠性(reliability)，当部分节点或链路失效时，仍保证路由尽可能可达。

本文主要研究基于名字解析的路由方案。传统名字解析方法如名字字典、DNS等，多基于树型结构或采用传统DHT方案，存在路径过长的问题。本文采用革命性的方式，摆脱传统路由限制，在新型可扩展路由基础上实现名字路由。

基于贪心嵌入的几何路由［9］将网络拓扑贪心嵌入度量空间，为每个节点分配一个坐标，根据坐标距离进行贪心路由。几何路由作为一种位置相关的可扩展路由方案，具备良好的可扩展特性:路由表只需保存邻居节点坐标;延展度上界和平均延展度可维持较低水平;任意两节点之间可能存在多条可用的路径;同时还支持节点间距离的计算。现已被用于解决互联网的路由可扩展问题。目前几何路由研究多集中在图的贪心嵌入、坐标压缩以及降低路径延展度等方面，属于位置相关路由的范畴，而对位置无关路由研究很少，即给定一个网络对象的名字，如何寻找该对象。

本文以几何路由为基础，提出一种通用的基于位置无关名字的几何路由方案——GRIN(geometric routing on location-independent name)，结合底层几何路由和上层名字解析实现名字路由。本文主要贡献在于:在几何路由基础上提出源路由和贪心路由相结合的混合几何路由(hybrid geometric routing，HGR)方案;基于稀疏群组(sloppy group)［5］思想提出基于双层稀疏群组的名字解析框架实现名字到位置的映射;分析了HGR和GRIN在节点状态以及路径延展度的理论上界;通过仿真模拟验证GRIN在路由表规模、路径延展度以及可靠性等方面都优于其他路由方法。

2 相关工作

可扩展的名字路由设计多基于可扩展路由。现有的可 扩 展 路 由 主 要 包 括 :层 次 路 由 (hierarchical routing)［10］、DHT 路 由［11］、紧 致 路 由 (compact routing)［5，12］和 几 何 路 由(geometric routing)［9，13］。后三者可广泛应用于名字路由。与本文相近的名字路由有基于DHT路由的VRR［11］和基于紧致路由的Disco［5］，二者均用于主机名空间，而本文可用于主机、内容或服务等多种网络对象的名字空间，支持扁平和层次名字。

DHT路由将名字分布式发布到网络节点，多与其他路由相结合实现节点间通信。VRR(virtual ring routing)［11］将DHT与源路由相结合。节点采用扁平名字，根据名字大小形成虚拟环，每个节点存储环上前驱和后继节点的物理路径以及邻居信息，(同时节点v与其前驱/后继u的物理路径上的每个节点都存储到v和u的物理路径)，路由时选择与目的节点名字大小最接近的节点转发消息。VRR能保证平均路由表项数为(n为网络规模)，但部分节点路由表项过多，且无延展度上界，最坏情况可达到O(n)。部分DHT 方案与 传统 IP 路由 相结合 ，如 αRoute［14］、MDHT［15］。αRoute基于符号划分提出树型的名字DHT方案，将名字根据其符号分布式发布到网络节点，为降低路径延展度，建立了DHT拓扑到底层拓扑的映射，但解析信息分布是否均匀依赖于对名字库的分析。MDHT基于解析域构建层次DHT，域内采用传统DHT方案，域间则为树型层次结构，名字被发布到本地解析域以及对应的上层域，虽然该方案支持本地解析，但本地解析失败易产生长路径。

紧致路由将部分拓扑信息压缩到节点地址或报文头部，路由表只需保存部分路由信息，从而达到路由表规模可扩展和路径低延展度的折中。Disco采用层叠网设计。底层采用位置相关路由NDDisco，通过邻域和LandMark(LM)信息实现节点间路由，上层通过稀疏群组实现名字解析(映射)。Disco路由表项达到，路径延展度≤7。NIHDLR［16］提出无标度网络上的名字路由，选择节点度大的节点作为LM节点，并基于LM实现名字解析，路径延展度降为min｛3，2+d｝，但加重了LM的负担。LM作为以上两种路由的重要节点，所有通信都要经过LM，LM可能会成为路由的瓶颈;同时，由于将路由信息嵌入节点地址，路由可靠性难以保证。

几何路由将网络拓扑嵌入度量空间，为每个节点分配一个度量空间的坐标，并基于坐标距离实现贪心路由。PIE［13］采用多层贪心嵌入方法，将嵌入分为 lbn层，在第 i层将图划分为2i部分，分别提取生成树并嵌入O(lb2n)维、l∞范数(norm)空间。PIE节点只需存储邻居节点坐标，在标度系数为2～3的无标度网络及部分随机网络中其延展度上界为O(lbn)，但PIE不支持名字路由。参考文献［17-19］提出几何路由上的名字路由方案，基于几种特殊的几何路由(如前缀嵌入几何路由、双曲空间嵌入几何路由)，将名字映射为度量空间上的坐标，直接通过贪心路由找到距离其最近的节点作为其解析节点。但以上方案均针对单一几何路由方案，不具备通用性，且解析信息分布难以保证均匀。

本文在几何路由基础上提出名字路由方案GRIN，对几何路由具有通用性，能同时满足可扩展、位置无关、低延展度和可靠性等需求，不同情况下，其节点路由表项分别为）或当底层路由路径延展度上界为O(k)时，名字解析的路径延展度上界达到O(2k+1)。

3 基于位置无关名字的几何路由

GRIN可分为位置相关路由和名字解析两部分。位置相关路由处于物理网络拓扑，采用混合几何路由方案为名字解析和节点间通信提供路由支持;名字解析处于逻辑的名字空间拓扑，将网络对象的名字映射为位置。下面首先介绍HGR，然后讨论基于双层稀疏群组的名字解析框架。

3.1 混合几何路由

新几何路由方案设计不是本节研究重点，本节主要目的是改进几何路由使其适用于名字路由。鉴于PIE实现方便、计算简单等特点，HGR选择在PIE基础上进行设计，但HGR具有通用性，其并不局限于PIE，同样适用于其他几何路由。下面首先明确基于贪心嵌入几何路由的基本表示和定义，然后给出HGR的具体方案。

给定图G(V，E)，G为无向连通图，V为节点集合，E为边集，对于图G中的任意节点v，Nv为v的邻居集合。(X，d)为度量空间，其中，X为空间集合，d为X上的度量(距离)。

定义1 ∃f∶V→X，f为 V到度量空间 X的映射，对∀v，u∈V，∃γ＞0，使得:

当D=1时，则称映射f为图G到X的等距嵌入。d′为G上的度量，γ为伸缩系数，D为形变系数。

定义2 ∃f∶V→X，f为 V到度量空间 X的映射，对∀v，u∈V，(u∉Nv)，∃w∈Nv，使得:

则称映射f为图G到X的贪心嵌入。即在度量空间X中，当数据分组到达任意非目的节点f(v)，总能找到一个邻居节点 f(w)，使得 f(w)到 f(u)的距离小于 f(v)到 f(u)的距离。

等距嵌入保证图嵌入度量空间后不发生扭曲形变，其满足贪心嵌入的条件;贪心嵌入则是为了将图嵌入度量空间，使节点之间仍满足贪心条件，进而保证贪心路由100%可达。

Kleinberg［9］证明了图G的生成树到某度量空间的贪心嵌入，即G到该度量空间的贪心嵌入。为将拓扑图贪心嵌入度量空间，HGR首先提取生成树，然后将生成树等距嵌入度量空间，最后结合源路由和贪心路由实现节点间通信。因此，HGR可分为3部分:生成树提取、生成树等距嵌入和混合路由。

3.1.1 生成树提取

Cvetkovski等人［20］研究发现对于基于生成树贪心嵌入的几何路由，生成树选择是影响延展度的主要因素之一，要保证低延展度，生成树的边应尽可能地与最短路径重合，并提出最大权重生成树(权重指最短路径经过该边的次数)和最小直径生成树两种探索性方法。

由于最大权重生成树和最小直径生成树分别在边权重获取和图核心节点查找等方面的限制，无法找到高效的分布式算法。因此，首先为每一个节点分配节点ID，ID由两部分组成:节点度和随机值。然后选择ID最大的节点作为根节点，其后每一个节点选择到根节点距离最小的节点作为父节点。具体实现可采用STP［21］。该方法可有效减小树的直径以及坐标长度，尽可能地保证低延展度。

3.1.2 生成树等距嵌入

对于生成树 T 中的节点 O，其坐标为(o1，o2，…，ok-1)，S为 O 的子节点集合，S=｛v0，v1，…，vs-1｝，s为子节点数量，s=｜S｜。

HGR将生成树T等距嵌入l∞范数空间，T的等距嵌入过程与PIE类似:假设已知节点O的坐标，首先为其子节点 vi分 配 一 个 哈 夫 曼 编 码然 后 根 据 编码和父节点的坐标计算 vi坐标Ci由两部分组成，一部分ci1来自父节点O的坐标，另一部分ci2根据编码获得，dT(vi，O)为 vi与 O在树上的边权值，按照式(3)、式(4)可获得节点坐标。具体例子如图1所示，节点a的坐标为3，其包含两个子节点:b和c，a分别为b和c分配哈夫曼编码:1(用“+”表示)和 0(用“-”表示)。对于节点c，ac边权重为2，由于a坐标3＞0，则前一部分坐标 ci1=3+2;由于c的编码为0，所以后半部分坐标为ci2=-2。由此可得 c 的坐标(5，-2)。

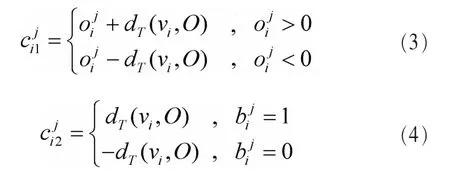
图1 生成树贪心嵌入

当父节点坐标为0时，子节点坐标完全来自编码，按照式(4)可获得节点坐标;当只有一个子节点时，子节点坐标完全来自父节点，无需对其编码，按照式(3)可获得节点坐标。初始时，根节点坐标设为0，经过一次生成树的遍历，可完成等距嵌入。

为降低坐标长度，HGR采用不等概率的哈夫曼编码分配坐标。对于节点O，des(O)表示节点O的子孙节点数量。节点O的子节点vi的子孙节点数量可表示为des(vi)。则vi的编码概率P(vi)=des(vi)/des(O)。编码概率越大，被分配的编码长度越短。在生成树层数不变的情况下，子树的节点数量越多，其编码越短，从而可有效降低节点平均坐标长度。

树嵌入之后，根据lp范数空间的度量公式可得到图G中的节点坐标距离。将X作为具有lp范数的k维度量空间，对于∀x，y∈X，在 X 上的度量(坐标距离)d(x，y)=｜x-y｜p，可表示为:

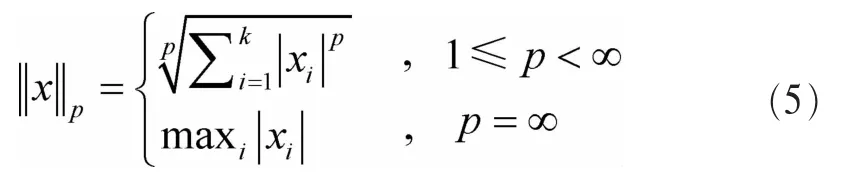
图 G上任意两点 u、v，其坐标分别为 Cu和 Cv，根据 l∞空间度量公式，则其坐标距离可表示为:

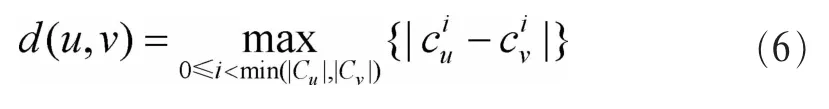
3.1.3 混合路由

贪心嵌入使得每个节点被分配一个坐标，可通过贪心路由进行通信。为支持名字解析，HGR引入邻域(vicinity)［5］的概念，基于邻域提出了源路由和贪心路由相结合的混合路由。

节点的邻域即距离该节点距离最近的前k个节点的集合。基于名字解析中的分组设计(网络节点在逻辑上被划分为多个群组)重新定义了邻域:节点s的邻域即每个群组中距离s最近的前k'个节点的集合。每个节点的路由表保存邻域和邻居的并集，并记录到各邻域节点的最短路径。

邻域可由集中式或分布式方法获得。集中式方法，每个节点根据网络拓扑计算以自身为根节点的最短路径树，然后选择每个群组中距离该节点最近的前k'个节点作为邻域节点;分布式方法，每个节点从其邻居节点获得邻居路由表中的邻域信息，建立自己的邻域。当某节点邻域发生变化时，将变化的路由表项通知其邻居节点，其邻居节点通过判断是否为某群组前k'个最近节点进行相应更新。

HGR整体采用贪心路由，局部采用源路由。当节点u收到目的节点为v的数据分组时，路由可分两种情况讨论:

· 若u为目的节点v，则路由结束;

·否则，采用贪心选择策略从路由表获得最优下一跳w。

数据分组通过源路由沿最短路径达到w，w重复以上过程，直到到达目的节点。当源路由部分路径失效时，则返回前一贪心节点，通知其路径失效，重新贪心以保证路由成功到达。

HGR的贪心策略与几何路由中常用的贪心策略不同。后者只选择距离目标最近的下一跳节点，其判断的依据是下一跳节点与目的节点的坐标距离。而HGR选择使当前节点和目的节点距离最小的邻居或邻域节点，其依据在于当前节点到邻居或邻域节点的最短路径距离与该邻居或邻域节点到目标节点的坐标距离之和是否最小。

对于任意节点 u，v，w(v∉Vu，w∈Vu)，Vu为 u 节点的邻居和邻域集合的并集，w为Vu中的节点，则节点u到v的贪心策略可表示为:，D(u，w)代表 u和w的最短路径距离，d(w，v)代表w和v之间的坐标距离。

3.1.4 HGR与PIE

HGR继承了PIE的多个优点:路由存在多条贪心路径，能尽量保证部分链路中断或节点失效时，路由仍可达;坐标距离为整数间的加减运算，坐标运算简单;支持加权图上的路由。

二者的主要区别表现在3个方面:PIE采用多层树嵌入，而HGR采用单棵树嵌入，可避免坐标过长及多个图嵌入产生的复杂通信;PIE采用等概率的哈夫曼编码随机分配坐标，而HGR采用不等概率编码，降低了平均坐标长度;PIE采用基于坐标的贪心路由，而HGR采用源路由和贪心路由相结合的混合路由，可有效降低路径延展度，并支持名字解析，但是邻域的引入会导致HGR路由表规模增大。

3.2 名字解析框架

GRIN名字解析与底层路由相互结合，采用稀疏群组［5］思想构建双层名字解析框架，充分利用底层物理拓扑中的节点坐标及邻域信息，有效限制名字解析时的路径长度。

3.2.1 双层名字解析框架

根据节点名字，稀疏群组可将网络节点分为多个相互独立的部分，形成逻辑的名字空间拓扑。每个节点的名字被散列成唯一的二进制串。由于名字结构对散列没有影响，因此，GRIN可同时支持扁平名字和层次名字。二进制串前k bit(k＜lbn)相同的节点可作为一个群组，网络被划分为2k个群组。如图2所示，GRIN将网络分为物理网络拓扑和逻辑名空间拓扑，在网络拓扑中节点被分为3个类(黑、白、灰)，每一类在名空间拓扑中代表一个群组，其中名空间拓扑中的椭圆即代表白色节点组成的群组。

图2 双层稀疏群组

对于群组内部节点，可继续按照稀疏群组的方法，根据二进制串的前k～k+h bit再分组，形成子群组。图2名字空间拓扑中椭圆上相同颜色的节点为一个子群组。可以根据网络对象的数量动态调整h的值，以便提高名字解析的效率和顽健性。当h=0时，只有一个子群组;当时，几乎每个节点都可作一个子群组。由此，由群组和子群组构成了GRIN的双层名字空间拓扑。

名字空间拓扑上的通信由群组间通信、子群组间通信以及子群组内部通信3部分组成。HGR的邻域在通信过程中发挥重要作用。由于邻域节点分布在不同群组，可将相互独立的群组关联起来，节点可通过其邻域与其他群组相连，继而实现了群组间通信。在群组内部，节点可建立子群组表，保存每个子群组中距该节点最近(坐标距离)的前l个节点的坐标信息，通过这些节点与其他子群组相连。同时，每个节点保存其所在子群组的所有节点的坐标信息，直接通过几何路由实现子群组内部节点的通信。以上3种情况，任意两节点间的通信都由底层HGR支持。

3.2.2 名字发布和解析

网络对象的发布以子群组为单位。当网络对象的名字/地址映射信息到达其所在子群组的某一节点时，该节点将映射信息广播到子群组内的所有节点，每个节点保存一份映射信息。其优势在于名字解析时，只需找到该子群组中任意节点即可完成解析，可有效减小名字解析的路径长度。

网络对象的名字解析和名字发布类似。对于节点s，V(s)为其邻域集合，G(s)为s所在的群组，SG(s)为s所在的子群组。当对象t的解析请求到达s时，可分3种情况讨论:

(1)若 t∈G(s)且 t∈SG(s)，表示 s保存了 t的解析信息，则可由s将t的名字映射成地址;

(2)若 t∈G(s)但 t∉SG(s)，则s从其子群组表获得节点u，使得t∈SG(u)，并将解析请求转发给 u，u重复过程(1);

(3)若 t∉G(s)，则s将请求转发到其邻域节点 v，使得t∈G(v)，在v中重复过程(1)、(2)完成名字解析。

GRIN的名字解析方案可有效降低名字解析的路径延展度。在名字空间拓扑上，GRIN至多两步就可完成名字解析:首先查询邻域节点;然后通过邻域节点查询名字所在的子群组节点。GRIN名字解析虽然建立在名字空间拓扑，但其将名字空间拓扑和物理拓扑更紧密的结合。名字空间拓扑可利用邻域以及坐标距离保证两步查询的路径为最短或近似最短。同时保证若查询节点周围存在最优的名字解析节点，则有很大概率被找到。

4 分析

4.1 节点状态

节点状态即节点中保存的用于路由和名字解析的信息的规模。HGR路由需要保存邻居节点集合和邻域节点集合的并集，这里认为邻居集合数量为常数，所以分析时只考虑邻域集合数量。GRIN则保存两类信息:名字解析表保存名字/地址映射信息;路由表保存邻域节点集合、子群组集合和子群组内的节点集合。

GRIN和HGR的名字解析表规模和路由表规模与策略选择有关。若选择名字/地址解析信息数量最优，则将每个节点代表一个子群组。假设群组数量为O(x)，子群组数量达到最大值O(n/x)，由于邻域数量与群组相等，则GRIN需要保存的路由信息为O(x+n/x)。当时，O(x+n/x)达到最优，此时，HGR和GRIN的路由表项规模可设置为名字解析表规模近似为O(B/n)(B为网络对象数量)。

若选择路由表规模最优，假设群组数量、子群组数量、子群组内部节点数量分别为O(x)、O(y)、O(z)，则路由表规模为 O(x+y+z)，根据均值不等式，当x、y、z均为时，HGR和GRIN路由表规模达到最优，为此时名字解析表规模为

4.2 路径延展度上界

HGR是基于PIE的几何路由，PIE已证明在标度系数为2～3的幂律图以及部分随机图上其延展度上界为O(1bn)。虽然HGR路径延展度的理论上界与PIE相同，但实验证明，由于邻域的使用，HGR的路径延展度要优于PIE。

GRIN名字解析的路径延展度则由HGR的延展度决定。假设HGR路由延展度上界为O(k)，则GRIN名字解析的路径延展度上界为O(2k+1)。可根据名字解析的3种情况分析:对于前两种情况，解析节点t分别为请求节点s自身或者与s在相同群组时，可直接解析或通过HGR路由实现解析，此时GRIN延展度上界为O(k)。当解析节点t与请求节点s在不同群组时，则s与t通过s的邻域u通信，可根据三角不等式分析其延展度上界。假设L(s，t)为s到t的实际路径长度，可表示为:

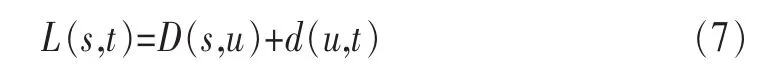
其中，D(s，t)为其最短路径长度，d(s，t)为 HGR 路由的路径长度。

根据三角不等式 D(u，t)≤D(s，u)+D(s，t)可得:

由于 u 为 s的邻域，则 D(s，u)≤D(s，t)，因此，可得 L(s，t)≤O(2k+1)D(s，t)。此时，GRIN 名字解析的延展度上界为O(2k+1)。

4.3 GRIN实现分析

GRIN实现方案简单可行，主要包括两种方案，可分别借鉴链路状态路由协议和距离向量路由协议。前一种方案可分为两步:节点通过链路状态广播LSA将其周围的拓扑信息广播给其他节点，每个节点建立链路状态数据库LSDB，最终得到一份完整一致的网络拓扑;基于网络拓扑，各节点选择一个相同的根节点构建生成树，并计算出自己的坐标、邻域节点及所在的群组和子群组。后一种方案可分为3步:采用SPF协议构建生成树，通过一次树遍历获取网络规模n，并通知给各节点;采用类似距离矢量算法，为每个节点寻找邻域节点;通过邻域节点获得群组以及群组内部节点信息。

5 仿真结果

本文基于C++设计了一种静态路由模拟器。为支持大规模模拟，采用集中式方法设计简化的模拟器，模拟器主要包括拓扑类和节点类。拓扑类保存所有节点，负责拓扑生成、路由表构建、名字发布和解析等。节点类保存节点ID、路由表、解析表、邻居链表以及统计信息等，并负责转发报文。拓扑生成主要由文件读取和由拓扑模型 (如ER模型、BA模型、GLP模型等)生成，拓扑生成过程中，每个节点被随机分配一个名字，并通过SHA-1将名字散列为128 bit的比特串。路由表构建需要完成生成树提取、贪心嵌入、邻域以及子群组获取，均可基于全局拓扑信息实现。名字发布/解析时，先设置源节点以及要发布/解析的名字，然后可调用各节点的转发方法实现路由转发。根据名字散列以及路由信息匹配选择转发的下一跳，并保存相关统计信息。下一跳节点继续进行匹配转发，直到达到解析节点，将发布信息存入解析表或根据解析表查询对应的解析信息。

分别在真实网络拓扑和虚拟网络拓扑进行仿真。实验中网络拓扑均作为无向连通图。真实网络拓扑为CAIDA［22］在2012年1月采集的10 683个节点的Internet AS拓扑数据集;模拟网络拓扑采用无标度网络的经典模型 (BA模型)［23］生成，设置其初始节点数为 3，平均节点度为 4。

Disco为目前较好的名字路由，基于主机名字空间设计，为与Disco及其底层路由NDDisco比较，采用与Disco相同的路由表规模并将子群组数量设置为最大，此时，GRIN与基于主机名字空间的路由类似。分别从坐标长度、节点的节点状态、路径延展度以及可靠性4个方面分析HGR和GRIN。

5.1 坐标长度

分别在真实拓扑和模拟拓扑测量等概率哈夫曼编码和不等概率哈夫曼编码产生的坐标长度，图3为真实拓扑下坐标长度分布，不等概率编码坐标长度集中在10～15，平均长度为14.94，而等概率编码坐标长度则集中在15～20，平均长度为16.17。图4为模拟拓扑在不同网络规模下的坐标平均长度，x轴取对数。可以看出，平均坐标长度与lbn近似呈线性关系，采用不等概率编码的平均坐标长度明显优于等概率编码的坐标长度。

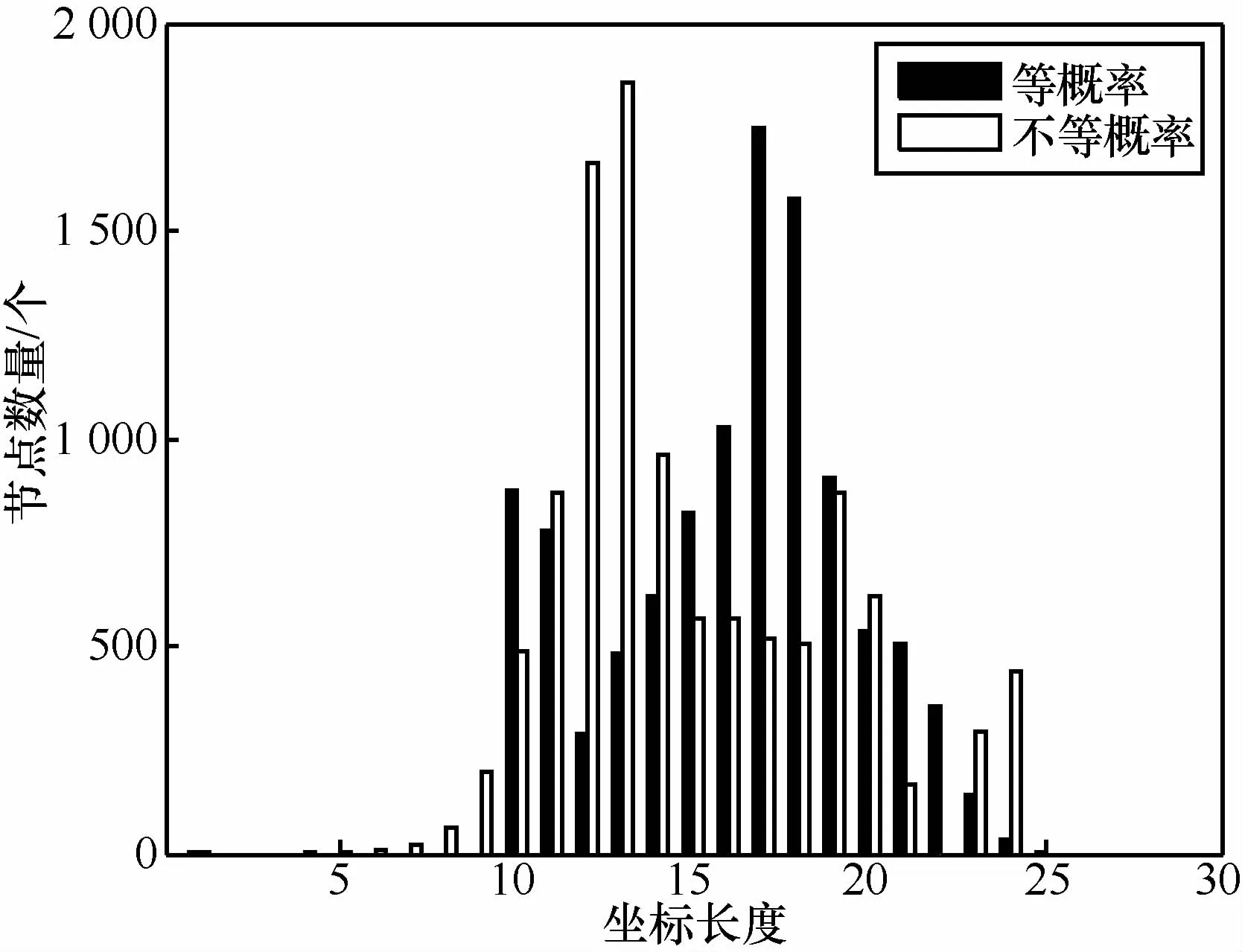
图3 节点坐标长度分布

5.2 节点状态

实验中节点状态只比较路由表项数量，本文分别从概率分布和平均节点状态两方面分析节点状态。图5为各路由方案的节点状态的概率分布。可以看出，各方案的节点状态分布都比较集中。位置相关路由所需的状态数均少于名字路由。对于具体路由方法，PIE存储节点状态数最少，主要集中在1～100，HGR节点状态主要集中在500附近，由于邻域的引入，HGR节点状态的数量要高于PIE。与基于紧致路由的方案相比，HGR和GRIN分别优于NDDisco和Disco。

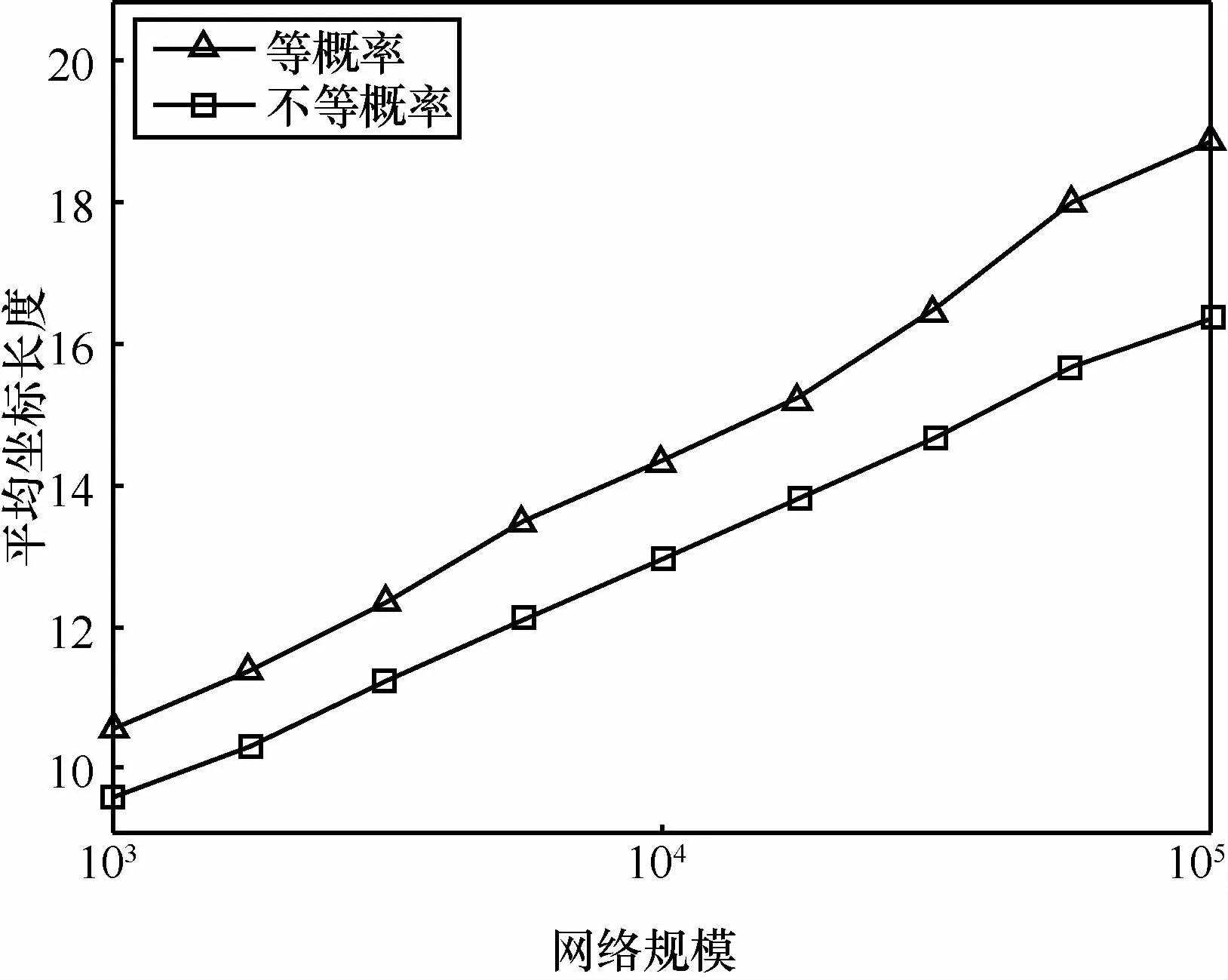
图4 平均坐标长度

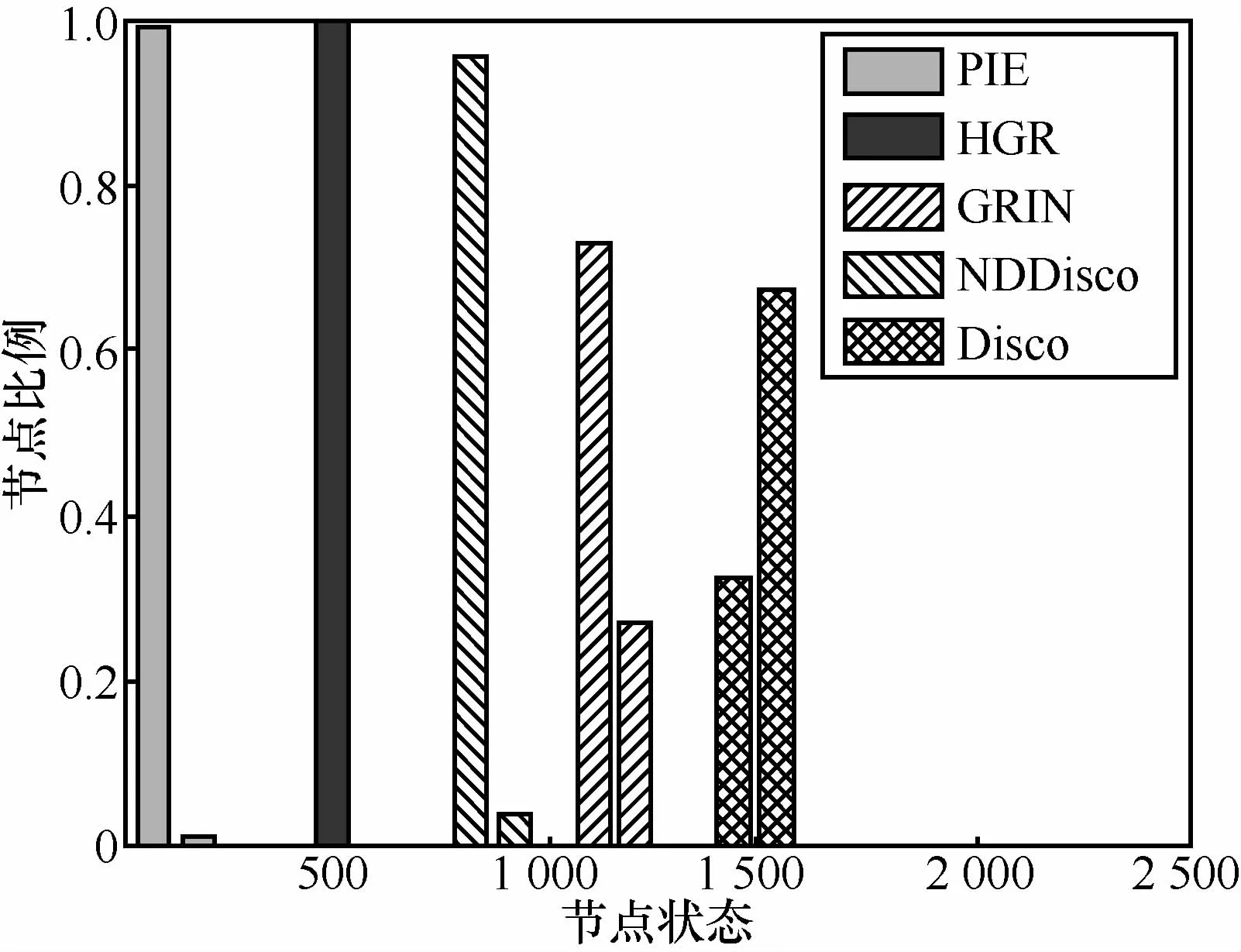
图5 节点状态概率分布

图6为不同网络规模下平均节点状态统计，可以看出，除PIE外，其他路由的节点规模均符合理论节点状态数的分析。GRIN存在一定的波动，主要原因在于不同规模网络可能使用相同数量的比特位划分稀疏群组，使得群组内节点数量出现波动，其有利于支持一定程度的网络规模变化。由于Disco节点状态数量基数较大，其波动不明显。

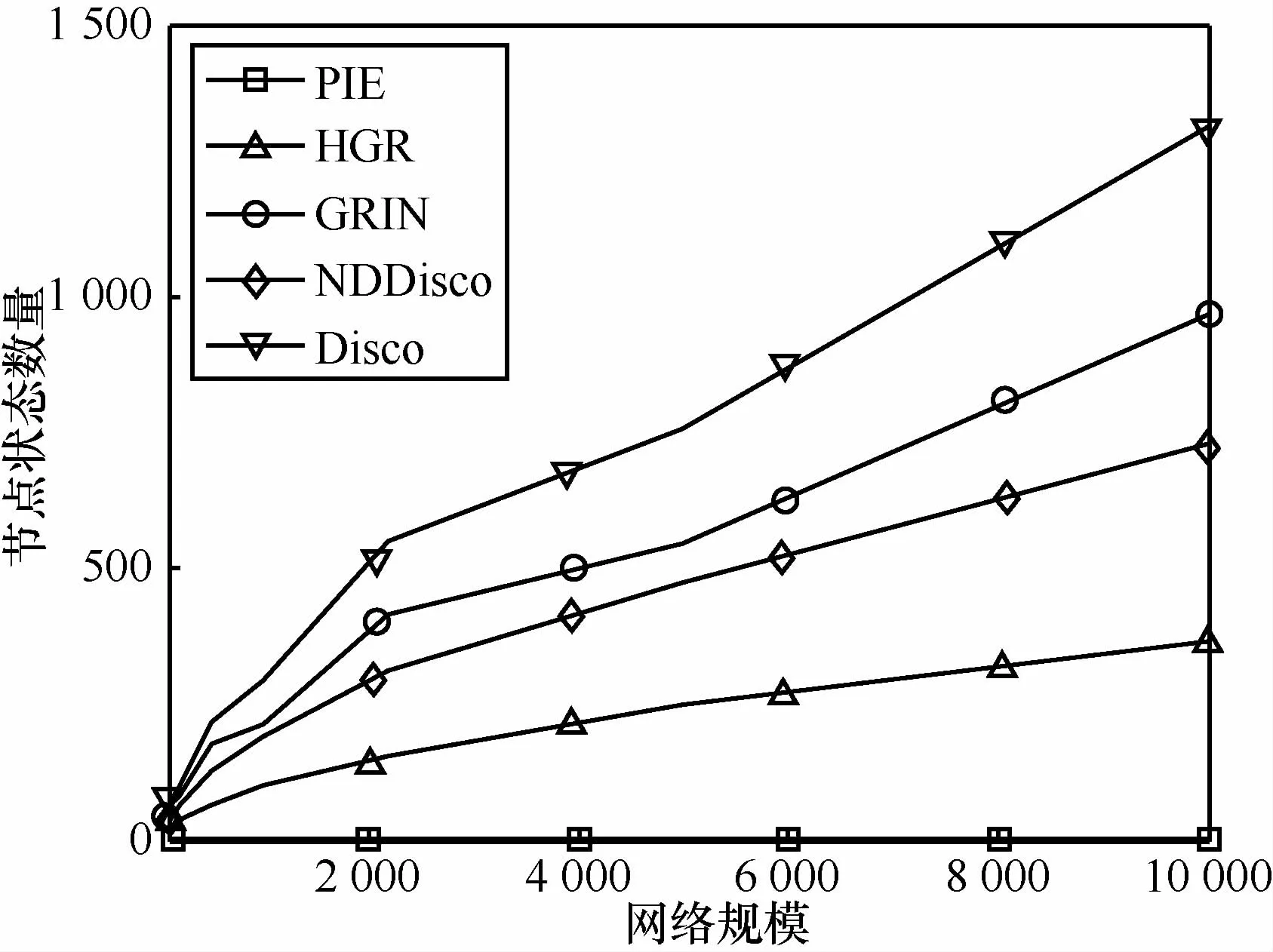
图6 平均节点状态

5.3 路径延展度

路径延展度反映了路径被拉伸的程度，是衡量路由可扩展性的重要标志之一。可扩展路由除保证路由表可扩展外，还需保证低延展度。图7分别为真实网络拓扑中位置相关路由和名字路由的延展度累积分布。对于位置相关路由，HGR是三者中最好的，HGR和PIE的结果远优于NDDisco。HGR的最短路径 (延展度为1的路径)比例占80%左右，而PIE和 NDDisco分别为75%和20%左右，且HGR的最大路径延展度不超过2.5。对于名字路由，GRIN优于Disco，二者最短路径所占的比例分别为19%和15%。最坏情况下，GRIN路径延展度不超过3.5。

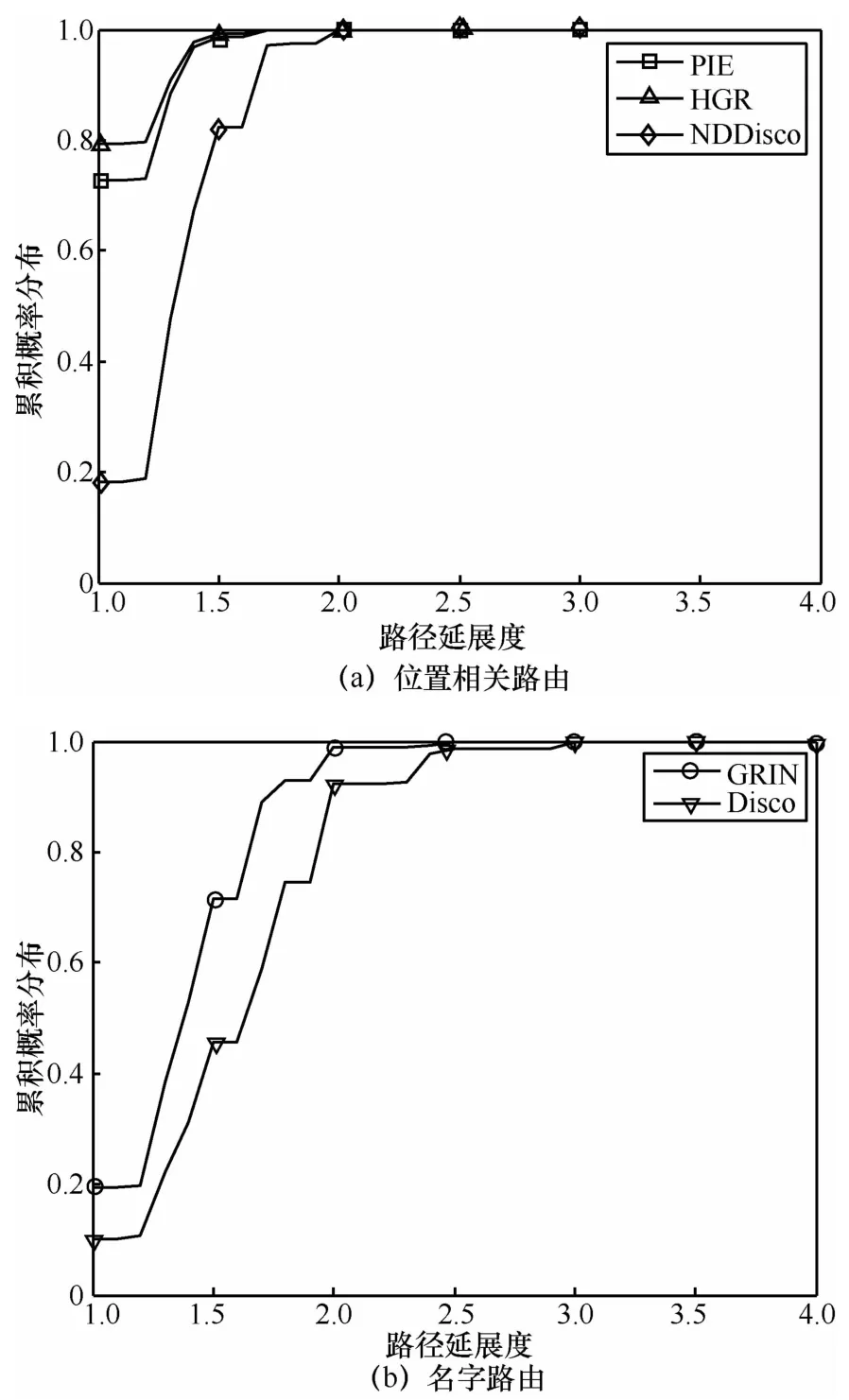
图7 路由路径延展度累积分布

为进一步说明路径延展度的区别，对比了平均路径延展度。图8为不同网络规模下平均路径延展度，各方案延展度大小关系与图7相同，GRIN平均延展度明显低于Disco。同一路由方案在不同网络规模下路径延展度波动很小，HGR和GRIN的平均延展度都小于1.5。可见，虽然HGR和GRIN在符合条件的图中理论延展度上界达到O(lbn)，但在具体网络拓扑中，延展度上界和平均延展度都能保持较低值，且远低于理论值。

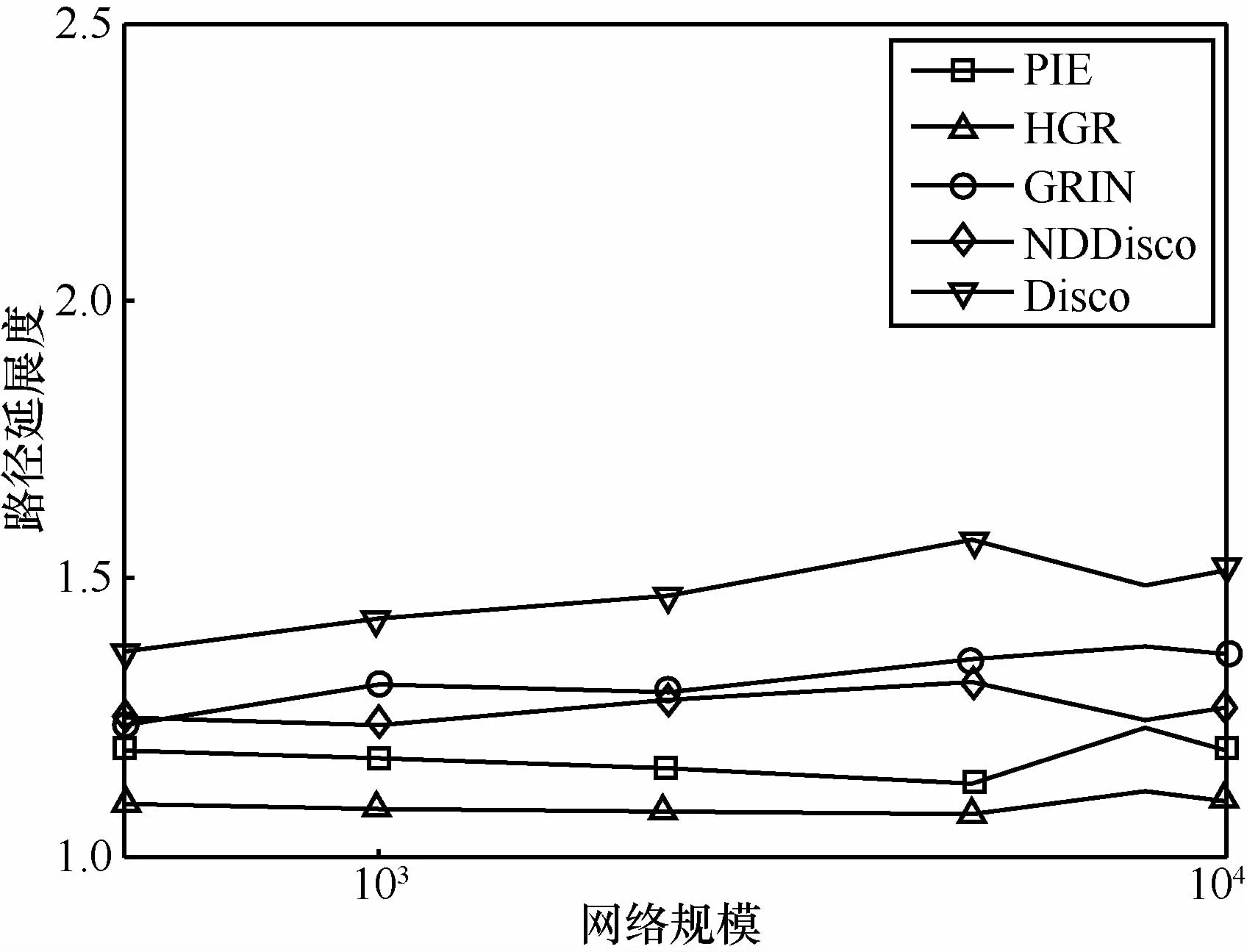
图8 平均路径延展度

为比较各方案路径长度，本文统计了不同网络规模下的平均路径长度(如图9所示)和最大路由直径(如图10所示)。可以看出，各路由方案的平均路径长度的大小关系与平均路径延展度的实验结果一致，GRIN平均长度优于Disco，接近于NDDisco。而对于最大路由直径，各路由之间的差距不明显，PIE与HGR完全重合，HGR和GRIN相比于NDDisco和Disco分别具备微弱优势。

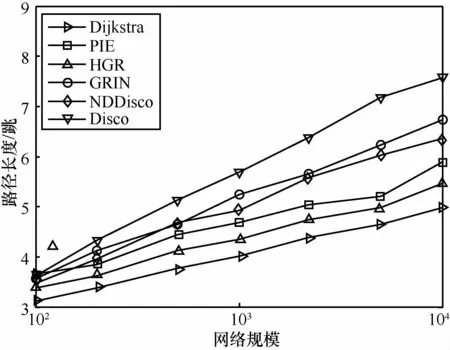
图9 平均路径长度

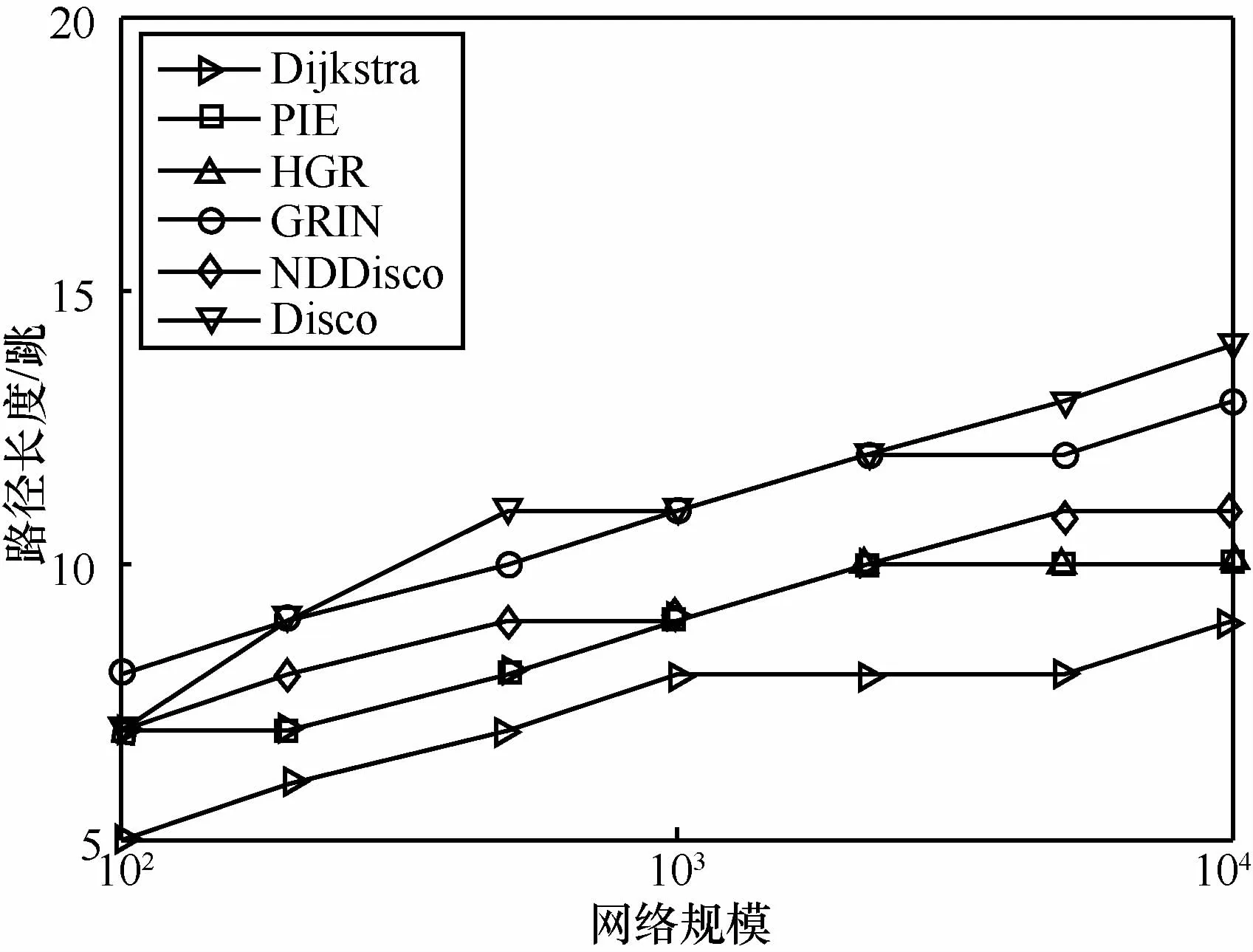
图10 最大路由直径

GRIN采用双层名字解析框架，子群组规模可动态调整，通过在子群组中选择较近节点进行名字解析，利于降低路径长度。为评价子群组规模与路径长度的关系，随机产生并发布50万个名字到真实网络拓扑，将子群组对应的比特串长度h分别设置为0、2、4，对每一个名字，随机选择一个节点作为源节点进行名字解析。图11为不同子群组规模下的名字解析路径长度分布。随着子群组规模的增大，解析路径的跳数逐渐减小，当h=4时，解析路径长度集中在2～6跳。由于网络对象以子群组为单位进行发布和解析，子群组规模扩大会导致解析表增大，因此在解析表规模可接受范围内，可尽可能提高子群组规模。

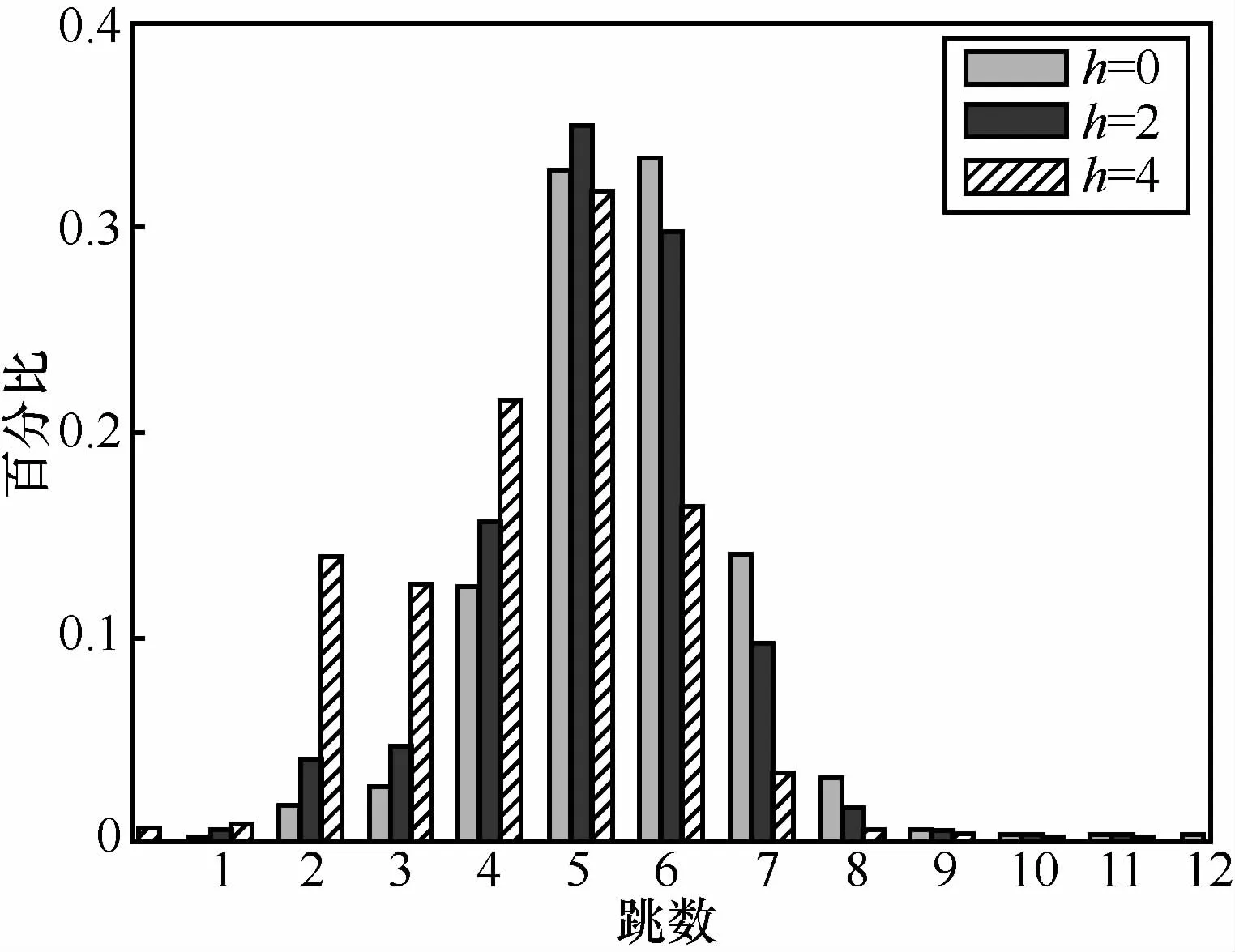
图11 路径长度分布

5.4 可靠性

假设路由过程中部分节点失效，而路由表还没有及时更新，在不考虑备份路径的情况下会产生一定程度的路由失败。在真实AS拓扑中，随机将一定比例的节点设为失效状态，同时随机选择不同的400万对节点对(节点对中不包括失效节点)路由，并统计路由失败率。

从图12可以看出，HGR和GRIN的路由失效率低于其他3种路由方式，即使在节点失效率达到10%的情况下，二者路由失败率依然低于15%。主要原因在于几何路由采用贪心方式进行路由，路径不唯一，同时邻域节点的加入为路由提供了更多的贪心选择。位置相关路由优于其对应的基于名字的路由，名字解析增加路径长度，必然导致基于名字的路由失败概率增大。

6 结束语

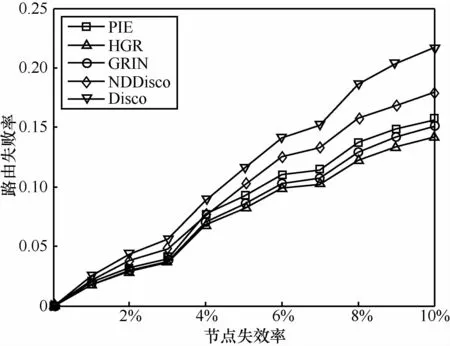
图12 路由失效率

本文在几何路由基础上提出了一种基于位置无关名字的可扩展几何路由方案GRIN。证明了路由表规模与网络规模呈亚线性关系，GRIN名字解析路径延展度上界与HGR的延展度上界存在线性关系，并通过仿真验证了GRIN具备可扩展、低延展、可靠性等特征。GRIN应用范围广泛，无论在当前Internet还是未来以内容为中心的网络中都具有巨大的发展潜力。不仅可用于主机名字空间解决当前网络IP语义过载引起的可扩展、移动等问题，还可应用于内容名字空间解决ICN的路由可扩展问题。

未来工作包括4个方面:第一，研究几何路由的贪心嵌入理论，本文中名字解析的路径延展度决定于底层路由，设计出具有良好延展度上界的几何路由是限制名字解析路径长度行之有效的方法;第二，在名字空间规模巨大情况下，名字/地址解析信息的存储和查询也将影响路由可扩展能力，因此研究有效的压缩存储和快速查询方法十分必要;第三，在协议层次实现GRIN，分析GRIN协议的消息负载;第四，将GRIN应用于ICN，该方法是解决内容中心网络路由可扩展问题的可行方法之一。

［1］AHLGREN B，DANNEWITZ C，IMBRENDA C，et al.A survey of information-centric networking［J］.Communications Magazine，2012，50(7):26-36.

［2］CAESAR M，CONDIE T，KANNAN J，et al.ROFL:routing on flat labels ［J］.ACM Sigcomm Computer Communication Review，2006，36(4):363-374.

［3］JACOBSON V，SMETTERS D K，JAMES D，et al.Networking named content ［C］//Proceedings of Conference on Emerging Networking Experiments and Technology，December 1-4，2009，Rome，Italy.New York:ACM Press，2009:1-12.

［4］The Locator/ID Separation Protocol:RFC6830:2013 ［S/OL］.［2015-7-25］.http://www.rfc-base.org/rfc-6830.html.

［5］SINGLA A，GODFREY P B，FALL K，et al.Scalable routing on flat names［J］.Eprint Arxiv，2013:1-12.

［6］GRITTER M，CHERITON D R.An architecture for content routing supportin the Internet ［C］//ProceedingsofUnix Symposium on Internet Technologies，March 26-28，2001，San Francisco，California，USA.New York:ACM Press，2001:4.

［7］KOPONEN T，CHAWLA M，CHUN B G，et al.A data-oriented(and beyond)network architecture［J］.ACM Sigcomm Computer Communication Review，2007，37(4):181-192.

［8］DANNEWITZ C，KUTSCHER D，OHLMAN B，et al.Network of Information (NetInf)-An information-centric networking architecture［J］.Computer Communications，2013，36(7):721-735.

［9］KLEINBERG R.Geographic routing using hyperbolic space［C］//Proceedings of IEEE International Conference on Computer Communications，May 6-12，2007，Anchorage，Alaska，USA.New Jersey:IEEE Press，2007:1902-1909.

［10］KLEINROCK L，KAMOUN F.Hierarchical routing for large networks:Performance evaluation and optimization［J］.Computer Networks，1977，1(3):155-174

［11］CAESAR M，CASTRO M，NIGHTINGALE E，et al.Virtual ring routing:network routing inspired by DHTs ［J］.ACM Sigcomm Computer Communication Review，2006，36(4):351-362.

［12］THORUP M， ZWICK U.Compactroutingschemes ［C］//Proceedings of the 13th Annual ACM Symposium on Parallel Algorithms and Architectures，July 4-6，2001，Crete Island，Greece.New York:ACM Press，2001:1-10

［13］HERZEN J，WESTPHAL C，THIRAN P.Scalable Routing Easy as PIE:a Practical Isometric Embedding Protocol ［C］//Proceedings of the 19th IEEE International Conference on Network Protocols，October 17-20，2011，Vancouver，Canada.New Jersey:IEEE Press，2011:49-58.

［14］AHMED R，BARI M F，CHOWDHURY S R，et al.alpha Route:A name based routing scheme for Information Centric Networks ［C］//Proceedings of the IEEE International Conference on Computer Communications，April 14-19，2013，Turin，Italy.New Jersey:IEEE Press，2013:90-94.

［15］DAMBROSIO M，DANNEWITZ C，KARL H，et al.MDHT:a hierarchicalname resolution service forinformation-centric networks ［C］//Proceedings of Conference of the Special Interest Group on Data Communication，August 15-19，2011，Toronto，Canada.New York:ACM Press，2011:7-12.

［16］唐明董，刘建勋，张国清，等.无标度网络上名字无关的紧凑路由研究［J］.计算机学报，2014，37(11):2353-2365.TANG M D，LIU J X，ZHANG G Q，et al.Name-independent compact routing in scale-free networks ［J］.Chinese Journal of Computers，2014，37(11):2353-2365.

［17］WANG L，WALTARI O，KANGASHARJU J.Mobiccn:mobility support with greedy routing in content-centric networks ［C］//Proceedings of IEEE Global Communications Conference(GLOBECOM)，December9-13，2013，Atlanta，USA.New Jersey:IEEE Press，2013:2069-2075.

［18］HOFER A，ROOS S，STRUFE T.Greedy embedding，routing and content addressing for darknets.Proceeds of Conference on Networked Systems，March 11-15，2013，Stuttgart，Germany.New Jersey:IEEE Press，2013:43-50.

［19］SUN Y，ZHANG Y，SU S，et al.Geometric name routing for ICN in dynamic world［J］.Communications，2015，12(7):47-59.

［20］CVETKOVSKI A，CROVELLA M.On the choice of a spanning tree for greedy embedding of network graphs ［J］.Networking Science，2013，3(1-4):2-12.

［21］PERLMAN R.An algorithm for distributed computation of a spanning tree in an extended LAN［J］.ACM Sigcomm Computer Communication review，1985，15(4):44-53.

［22］The IPv4 routed/24 AS links dataset ［EB/OL］. ［2015-07-15］.http://www.caida.org/data/active//ipv4-routed-topology-aslinksdataset.xml.

［23］BARABASI A L，ALBERT R.Emergence of scaling in random networks［J］.Science，1999，286(5439):509-512.

Scalable geometric routing scheme based on location-independent names

SUN Yanbin，ZHANG Yu，ZHANG Hongli，FANG Binxing
School of Computer Science and Technology，Harbin Institute of Technology，Harbin 150001，China

Name-based routing has become one of the hot topics in future network.However，due to the sustained growth of the size of nodes and information，the scalability issue is becoming one of the bottlenecks of name-based routing.As a new type of scalable routing，geometric routing provides both scalable routing tables and low routing paths，but it is difficult to support name-based routing.A universal scalable geometric routing scheme based on location-independent names(GRIN)was proposed.GRIN implemented a hybrid geometric routing(HGR)combining greedy routing with source routing，introduced a distributed name resolution using 2-level sloppy groups.Then the state and the path stretch upper bound of GRIN were analyzed.The simulation results show that GRIN guarantees scalability，low stretch and reliability.It outperformanced other similar routing schemes.

geometric routing，name resolution，name-based routing，scalability

s:The National Basic Research Program of China (973 Program)(No.2011CB302605，No.2013CB329602)，The National Natural Science Foundation of China(No.61202457，No.61402149)

TP301

A

10.11959/j.issn.1000-0801.2016001

2015-07-25;

2015-12-08

国家重点基础研究发展计划(“973”计划)基金资助项目(No.2011CB302605，No.2013CB329602);国家自然科学基金资助项目(No.61202457，No.61402149)

孙彦斌(1987-)，男，哈尔滨工业大学计算机科学与技术学院博士生，主要研究方向为可扩展路由和未来网络。

张宇(1979-)，男，博士，哈尔滨工业大学计算机科学与技术学院副教授，主要研究方向为网络安全、网络测量和未来网络。

张宏莉(1973-)，女，博士，哈尔滨工业大学计算机科学与技术学院教授、博士生导师，主要研究方向为网络安全、网络测量和网络计算。

方滨兴(1960-)，男，中国工程院院士，哈尔滨工业大学计算机科学与技术学院教授、博士生导师，主要研究方向为网络与信息安全、并行计算和分布式系统。