基于元胞自动机的食物链各物种斑块数量演化的数值模拟研究

鄂道阳 高军晖

摘 要：该文运用元胞自动机来模拟食物链中物种斑块数量的演化。在第一部分引言中回顾了元胞自动机在食物链中的应用；在第二部分中定义了物种斑块；第三部分是模拟和计算，包括元胞自动机模型的假设、初始化、元胞自动机的运行、斑块数量的统计等内容；第四部分对斑快的时间变化进行了分析；第五部分是讨论与结论。研究发现，当食物链各物种的数量变化趋向稳定状态后，各物种斑块的数量变化，也会呈现出稳定的状态。

关键词：食物链 斑快 元胞自动机 演化

中图分类号：O242 文献标识码：A 文章编号：1674-098X（2016）02（a）-0060-03

食物链是在食物网中由基本的生产者开始，结束于顶端的捕食者，食腐动物，或是分解者的线性关系。食物链可以通过生物的食谱显现出他们各自的关系，它的每一层也代表了不同的营养层。食物链不同于食物网，因为食物链食物链只是一条每一层由一种生物组成的结构而食物网则是复杂的不同动物的关系聚合后的产物。食物链最初由African-Arab科学家哲学家Al-Jahiz提出，后来在一本由Charles Elton写的，在1927年出版的书中得到推广，这本书同时引出了食物网理论[1-4]。

元胞自动机（Cellular Automaton，以下简称CA）是冯·诺依曼（John Von Neumann）20世纪60年代提出的用于模拟生命系统所具有的自复制功能模型，是一个构造简单，空间和状态变量离散，且状态有限的模型。

Dewdney（1984）可能是第一个用CA研究捕食与猎物系统的人[5]，他用环面上的元胞系统和冯·诺依曼邻居（上下左右4个方向）研究了鲨-鱼系统。此后，这方面的研究逐步展开。

一般来说，元胞自动机主要模拟食物链中的物种变化，但是也有比较特殊的，如Robert M.Itami（1994）就使用过元胞自动机来模拟物种的密度[6]。Hawick（2010）在100 000大小的元胞区域，对两种群捕食与猎物系统进行空间分析[7]。

高竹等（2013）利用元胞自动机对3种群的捕食与猎物系统进行数值模拟研究[8]。该文在文献[8]的程序基础上，运用元胞自动机来模拟斑块的演化，注重的就是斑块的数量与时间的变化规律。

1 物种斑块的定义

为简单起见，我们构建一个6×6大小的只有一个物种的二维元胞空间，如图1所示。其中黑色的格点表示被物种占据。

如果那些被占据的格点彼此相邻，则它们就形成一个斑块。相邻的判断准则与元胞自动机一致，这里采用冯-诺依曼（Von.Neumann）型，即一个元胞的上、下、左、右相邻4个元胞为该元胞的邻居[4]。

图1中，一共有8个斑块，从上往下、从左往右，8个斑块的面积分别是1、1、3、2、2、1、1、2个单位。最大斑块的面积为3。

2 模拟与计算方法

2.1 模型的假设

我们采用的方法与文献[8]一致，食物链由植物、食草动物和食肉动物组成。这里，植物、食草动物、食肉动物分别用草、兔子、狼作为代表。兔子与草之间、狼与兔子之间构成捕食与猎物的关系。

采用的元胞自动机是一个二维矩形区域，由矩形方格组成，每个方格由草或兔子或狼占据，也可能是空地。采用冯·诺依曼邻居，即兔子和狼均只能以上、下、左、右4个方向移动或捕食，而草不能移动。

2.2 初始化

首先设定好空地、草、兔子、狼占据方格的概率，然后遍历所有的矩形方格，对于每一个方格，用蒙特卡洛方法（Monte Carlo）模拟，决定该方格是被4种中的哪一种占据。初始化还包括两类动物各自的饥饿时间，3个物种各自的生育区间等参数。图2是初始化的一个实例，其中浅白色表示空地，深灰色表示草，浅灰色表示兔子，黑色表示狼。

2.3 运行元胞自动机

假设元胞自动机由100×100的方格组成，一共有1万个格式，我们把1万次模拟作为1个步长，这样可以保证平均每个元胞有1次机会进行演化。图3是元胞自动机运行结果实例。

2.4 斑块数量的统计

为了获得演化中的斑块信息，我们每100步就输出一个矩阵，100行，每行100列。矩阵中的元素分别是0、1、2、3，代表空地、草、兔子、狼。

我们另外编写了一个程序，计算矩阵中0、1、2、3的斑块数量。模拟的结果见第4部分。

3 结果与分析

表1显示了我们从20个矩阵（时间序列）中获得的斑块数量。

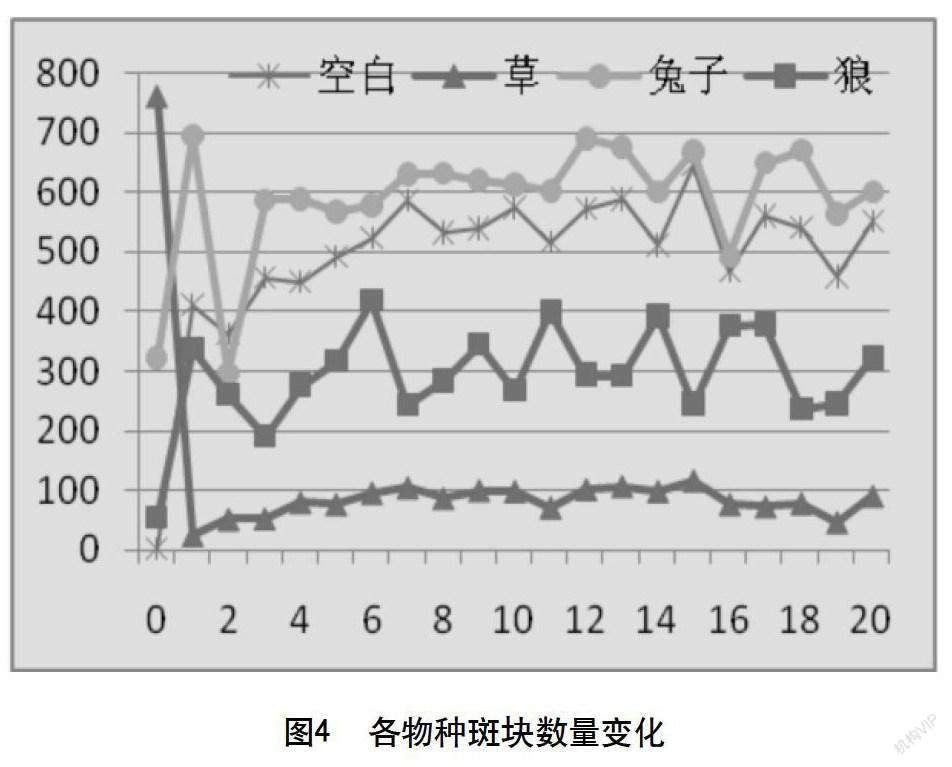
我们把表1中的数据绘制成时间曲线，如图4所示。

从图4中我们可以看出，空地的斑块数量一开始迅速上升，这是因为在一开始，3个物种的密度都不大，造成空地的密度大，以至于空地全都连成一片，这个可以从图2中看出来。随着时间的推移，其他3个物种的密度逐步增加，空地的密度就逐步减少，原先连成一片的大空地斑块不断地分解成了小空地斑块、更小的空地斑块，因而空地斑块的数量逐步增加。大约在7个步长开始，空地斑块的数量开始出现起伏并且稳定在500～600之间。

草的斑块数量的变化正好与空地相反。相对于兔子和狼，在初始化时，草的密度更大，因此，一开始草的斑块数量明显多于兔子和狼的斑块数量。随着时间的推移，草的快速生长使得草的密度逐步增加，原来分散的斑块连成一片，使得草的斑块数量迅速下降，这个可以从图3中看出来。

兔子的斑块数量，一开始有大的震荡，然后变得比较平稳。狼的斑块数量的变化，与兔子类似。

从图4中我们可以发现，在经历了一段时间之后，四种斑块的数量都脱离了大幅变化，趋向了平稳。平稳状态中，草的斑块块数量最小，大约在100左右，其次是狼的斑块数量，大约在250～400之间，空地的斑块数量大致在500～600之间，而兔子的斑块数量在600左右。

4 讨论和结论

该文运用元胞自动机来模拟物种斑块数量的演化。研究发现，当食物链各物种的数量变化趋向稳定状态后，各物种斑块的数量变化，也会呈现出稳定的状态。

然而，限于研究水平，笔者没有考虑各种可能的情况，这也是今后继续努力的方向。

参考文献

[1] Angela Mclean，Robert May.Theoretical Ecology：Principles and Applications[J].W.b.saunders Company Philadelphia Pa，2007（16）：1147-1152.

[2] Elton，C.S.Animal Ecology[M].London，UK.： Sidgwick and Jackson，2001.

[3] Allesina，S.，Alonso，D.，Pascal，M.A general model for food web structure[J].Science，2008（5876）：658-661.

[4] Egerton，F.N.Understanding food chains and food webs，1700-1970[J].Bulletin of the Ecological Society of America，2007（1）：50-69.

[5] Dewdney，A.K.Sharks and fish wage an ecological war on the toroidal planet Wa-Tor[J].Scientific American，1984，251（6）：14-20.

[6] Robert M.Itami.Simulating spatial dynamics： cellular automata theory[J].Landscape and Urban Planning，1994（1）：27-47.

[7] KA Hawick.Spectral Analysis of Growth in Spatial Lotka-Volterra Models[C]//K.A.HawickProc.IASTED International Conference on Modelling and Simulation，2010.

[8] 高竹.基于“元胞自动机”的食物链模拟软件[J].生物学教学，2013（3）：41-42.