部分水解聚丙烯酰胺与蠕虫状胶束在微米级毛细管中的驱替粘度

陆业昌李文宏张永强李学丰董金凤,*

（1武汉大学化学与分子科学学院，武汉 430072；2低渗透油气田勘探开发国家工程实验室，西安 710021；3中国石油长庆油田分公司勘探开发研究院，西安 710021）

部分水解聚丙烯酰胺与蠕虫状胶束在微米级毛细管中的驱替粘度

陆业昌1李文宏2,3张永强2,3李学丰1董金凤1,*

（1武汉大学化学与分子科学学院，武汉 430072；2低渗透油气田勘探开发国家工程实验室，西安 710021；3中国石油长庆油田分公司勘探开发研究院，西安 710021）

部分水解聚丙烯酰胺（HPAMs）被大量地用作三次采油中驱替液的增稠剂，表面活性剂在一定的条件下可以通过自组装形成蠕虫状胶束，具有与高分子相似的增稠的作用。本文在半径为1–10 μm的毛细管中，分别考察了HPAMs与蠕虫状胶束的微观驱替行为，研究结果表示毛细管内腔的尺寸限制了这些非牛顿流体的增稠作用。随着毛细管半径的减小，聚合物溶液的剪切变稀越剧烈，甚至从非牛顿流体转变为牛顿流体的流体行为。结合驱替研究和超滤、电镜的结果，证明了高分子的缠绕结构在毛细管中已被破坏。通过对比驱替数据，蠕虫状胶束在毛细管中能够更大程度地保留宏观的粘度，我们提出表面活性剂能够通过自组装修复被破坏的缠绕结构，比高分子聚合物在微观有限空间中有更好的增稠能力。

微米级毛细管；驱替粘度；部分水解聚丙烯酰胺；蠕虫状胶束；毛细管压力

1 Introduction

Low or ultra-low permeability oil and gas resource is abundant and has a great potential of exploration and development. Oil production in low permeability reservoirs increases continuously and the proportion in production components is increasing yearly. Pore throats or channels typically range from about 0.1 to 1 μm in the low permeability reservoir. Water-oil displacement in these reservoirs was assumed as a piston-like shock and the viscous fingers was investigated widely both using numerical simulation and experimented techniques1,2. Enhanced oil recovery （EOR） was developed to be an economic technique in increasing production from the oil left in the ground. Based on the capillary number, Ca = ηV/γ, where η is the viscosity of the liquid, V is a characteristic velocity, and γ is the surface or interfacial tension between the two fluid phases, both increasing the viscosity of the liquid and decreasing the interfacial tension are effective ways to increase Ca above 10–5which is favorable to reduce the viscous fingers3. Hydrolyzed polyacrylamides （HPAMs） have been widely applied to enhance the viscosity of aqueous injectants in pores4,5. However, the in-situ viscosity is less than the bulk viscosity due to the existence of a depleted layer near the pore wall6,7. The effect of employing polymers has been a focus in research for the last two decades8–10. One of the challenge is developing feasible insitu experimental techniques to study the flow behavior and immiscible two-phases displacement. A number of experimented techniques were reported to investigate the cores over 100 μm reserviors11–13. And some numerical simulation methods were established to estimate the behavior of fluid displacing in the nanopores14,15. We developed a digital video technique to visualize the interface movement in microscale capillary. The radii of the capillary can be as small as 1 μm due to the availability. Based on the Washburn equation, two-phase or three-phase flows have been investigated and the size of capillary was found to play a critical role in the displacement velocity and capillary pressure16–23.

The present work employs commercial samples of HPAMs with different molecular weights as the displacing phase in quartz capillaries with radii ranging from 1 to 10 μm. Immiscible two phase displacement such as liquid-gas and liquid-liquid flow are investigated. The shear-thinning behavior of HPAMs in bulk is characterized. The capillary size effect on the in-situ viscosity during the capillary displacement is established. Significant difference between bulk viscosity and in-situ viscosity was found. Filtration and transmission electron microscopy （TEM） were employed to explain the results. In comparison, worm-like micelles （WLMs） are known as the “living polymers” which can be constructed by the self-assembling of surfactant molecules, was employed to replace HPAMs in the displacing agent, and the in-situ viscosity was characterized.

2 Materials and methods

2.1 Materials

Glycol （≥ 99.0%） and n-decane （≥ 99.0%） were obtained from Sinopharm Chemical Reagent Co., Ltd. Glycol was used as received and diluted by deionized water to required concentration. n-Decane was used as the oil phase after being purified following a text book process until the decane/water interfacial reaches 50 mN·m–124. Polyacrylamides with different molecular weights listed in Table 1 were supplied by SNF FLOERGER and used as received. The polymer solutions were prepared by introducing weighed amounts of HPAM in ultrapure deionized water （Milli-Q system） and stirred by 60 r·min–1at least 24 h to ensure complete dissolution, then left at 25 °C for 3 d before any measurement. The WLM samples were prepared following the previous report25, the concentration of sodium oleate （NaOA, > 99%, from STREM CHEMICALS） was 50 mmol·L–1, and 1-［2-（4-phenylazo-phenoxy）-ethyl］-3-methylimidazolium bromide （C0AZOC2IMB, synthesized by our group） was 17.5 mmol·L–1, the mole ratio ［C0AZOC2IMB］/［NaOA］ was 0.35. 99.99% nitrogen was used as the gas phase. Capillaries of high-purity quartz （> 99.99% of SiO2） were purchased from Polymicro Technologies （U.S.）.

2.2 Surface or interfacial tension

The surface tension γ and the interfacial tension between aqueous phase and decane γ12were measured via Pendant Drop method （DSA100 droplet shape analysis, Krüss, Germany） at 25 °C. Corresponding experimental results were given in Table S1 in the Supporting Information.

2.3 Rheological measurements

Measurements were performed on a RS 600 stress-controlled rheometer （HAKKE RS600, Thermo Fisher Scientific, Germany） using a couvette geometry Z20 according to the fluid viscosities. A Peltier-based temperature controller maintained the sample at 25 ºC. The samples were equilibrated for at least 30 min before measurements. A solvent trap was used to minimize sample evaporation.

2.4 Capillary tubes

The radii of the capillary were measured by the method referred to the previous literature26–28. Dry capillaries were first saturated with water for an hour, and then, liquid in capillaries was expelled by blowing nitrogen gas before experiments. The determined results of the capillaries used in this study were 1.13, 2.88, 5.38, 9.18 μm, respectively.

Table 1 Molecular weight of HPAMs

2.5 Displacement

The experiment setup was designed according to the reported apparatus28. In all of the experiments, the capillary was cut into a length L ≈ 180 mm. In the liquid-gas displacement, the experiments were setup by the same way as the method of determination of capillary radii. In the liquid-liquid displacement, the capillary was first placed in one end into the oil reservoir, and then the capillary would be saturated with oil spontaneously until it was completely saturated. Subsequently, the oth-er end of capillary was placed into the water solution reservoir and the solution could displace the oil phase spontaneously. After that, the capillary was placed horizontally, attached each end with a reservoir containing the displacing and displaced phases, respectively. Following the procedure reported earlier26–28, the displacement rate v was measured from the time required for the interface of liquid-gas or liquid-liquid system to travel a very small distance ΔL = 500 μm （ΔL << L） at a specific point.

2.6 Filtration

Microporous filters with pore diameters 2, 5, 10, 20 μm were purchased from Xingya purification materials plant （Shanghai）. The viscous polymer fluids were forced to pass the microporous filters under external pressure of 100 kPa.

2.7 Transmission electron microscopy

The configuration of HPAMs molecules were observed on a JEM-2100 TEM operated at an acceleration voltage of 200 kV. Samples for TEM observation were prepared as follows. One drop of sample with a concentration of 1000 mg·mL–1was placed on a carbon-coated copper grid and the excess fluid was drained off with a filter paper. Then, a drop of 2% （w, mass fraction） aqueous phosphotungstic acid solution was added and the residue of the aqueous solution was removed with a filter paper after several minutes. The samples were finally dried at room temperature prior to measurement.

3 Results and discussion

Washburn equation describes Newtonian fluids displacement in the capillary assuming that the viscosity of the fluid is constant. The relationship between the displacement rate and external pressure is linear. The polymer solution investigated here is a shear-thinning fluid. Its viscosity of polymer solution decreases with the increase of shear rate, corresponding to the displacement rate in the capillary. The displacement rate of polymer solution is predicted to be a power-law function of the external pressure by the theory and previous experiments in which the flows are displacing in capillary over 100 μm11–13. Fig.1 shows the shear viscosity of polymer solutions and wormlike micelle solution. Polymer and worm-like micelle solution is a shear-thinning fluid, and the viscosity curves show a Newtonian plateau at low shear rate and drop at high shear rate for the breakage of entanglement of the long chains. The viscosity drop can be seen as a power-law function of shear rate.

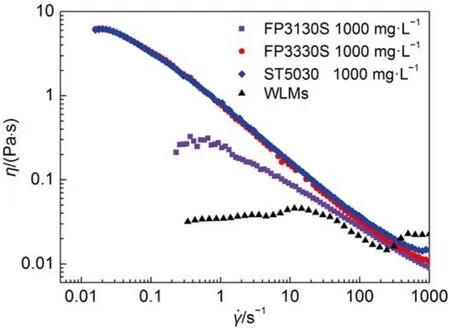
Fig.1 Shear viscosity vs shear rate for the non-Newtonian systems

In the classic Washburn equation16, for the liquid-gas flow, the relationship between displacing rate v （the rate of meniscus displacement） and external pressure ΔP is

where r is the capillary radius, η is the viscosity of the fluid, Pcis the capillary pressure, and L is the length of the fluid. And for the liquid-liquid flow,

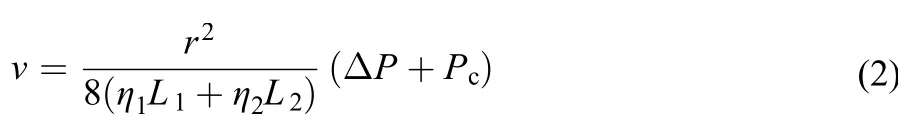
where ηiand Liare the viscosity and length of each phase, respectively.

The capillary pressure at each interface caused by interfacial tension could be written as Young-Laplace equation

where γ is the tension of the surface or interface, θ is the wetting contact angle. Measured fluids firstly saturate the capillary and are expelled by blowing nitrogen gas before experiments, so the capillary is pre-wetted by the fluid and the contact angle θ can be treated as 0°.

Equations （1）–（3） are used to describe the kinetics of mutual displacement of the Newtonian fluid whose viscosity is taken as a constant value η. In a cylindrical capillary with radius r, the displacing rate v and external pressure ΔP show a linear relationship in which the length of each phase Lican easily be identified, with slope k = r2/8ΣηiLi. So the in-situ viscosities of fluid can be calculated from this slope of the v–ΔP line.

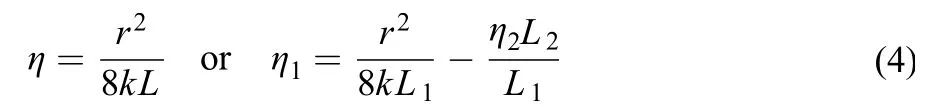
The in-situ viscosities of some known Newtonian fluid, including decane and 65% glycol aqueous solution, measured by this displacement method are shown in Table 2. Clearly, the viscosity measured by displacement method fits well with that by rheometer. The Newtonian fluid′s viscosity keeps the same in different sizes of capillaries, which assures that the displacement method is feasible.

Table 2 Viscosity of known fluids at 25 ºC

For shear-thinning fluid, the in-situ viscosity is a function of the shear rate. The power law is the simplest one of the models which is given by the relation

where C is the consistency factor,is the shear rate, and n is the flow behavior index. The power-law is usually used to model shear-thinning behavior when n = 1, the value of C is equal to the viscosity of Newtonian fluids.

If the fluid is treated as a power-law model, the Washburn equation of liquid-gas flow could be extended as29

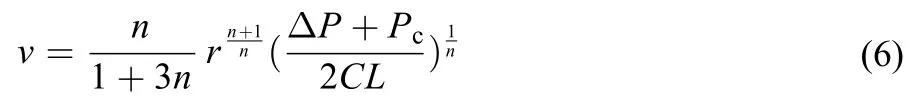
The relationship between displacing rate v and total pressure drop （ΣP = ΔP + Pc） could be a power-law function with flow index 1/n when the length of liquid L is identified in specified capillary, where Pccan be calculated by equation （3）.

3.1 Liquid-gas displacement

Fig.2 shows the displacement rate as a function of the external pressure when the HPAM solution with molecular weight 2 × 106Da flowed into the microscale capillaries. Apparently, the linear relationship only holds for certain curves, meaning that the fluid is non-Newtonian type, and the viscosity is not constant. The experimental data can be fitted with power-law function （equation （6） and all the fittings have a correlation coefficient of r2≥ 0.99. From this fitting, the consistency factor C and the flow behavior index n can be calculated which are presented in Table 3. It can be seen clearly that C decreases and n increases with the decrease in the capillary radius, indicating that the smaller the size of capillary is, the fluid behavior is more approaching the Newtonian fluid. For example, in the capillary with radius of 1.13 μm （see Fig.2a）, the displacement rate is completely a linear function of the external pressure （also can be considered as that the power-law index increased to 1）, the viscosity does not change with the change of displacement rate, which can be represented by the classic Washburn equation（equation （1）. Furthermore, the HPAMs with different molecular weights show similar result （See Figs.S1, S2 in the Supporting Information）. The results suggest that when the HPAM solution flows into the capillary with radii below 10 μm, the viscosity of fluids decreases and turns to the Newtonian type in the capillary with a radius of 1.13 μm.

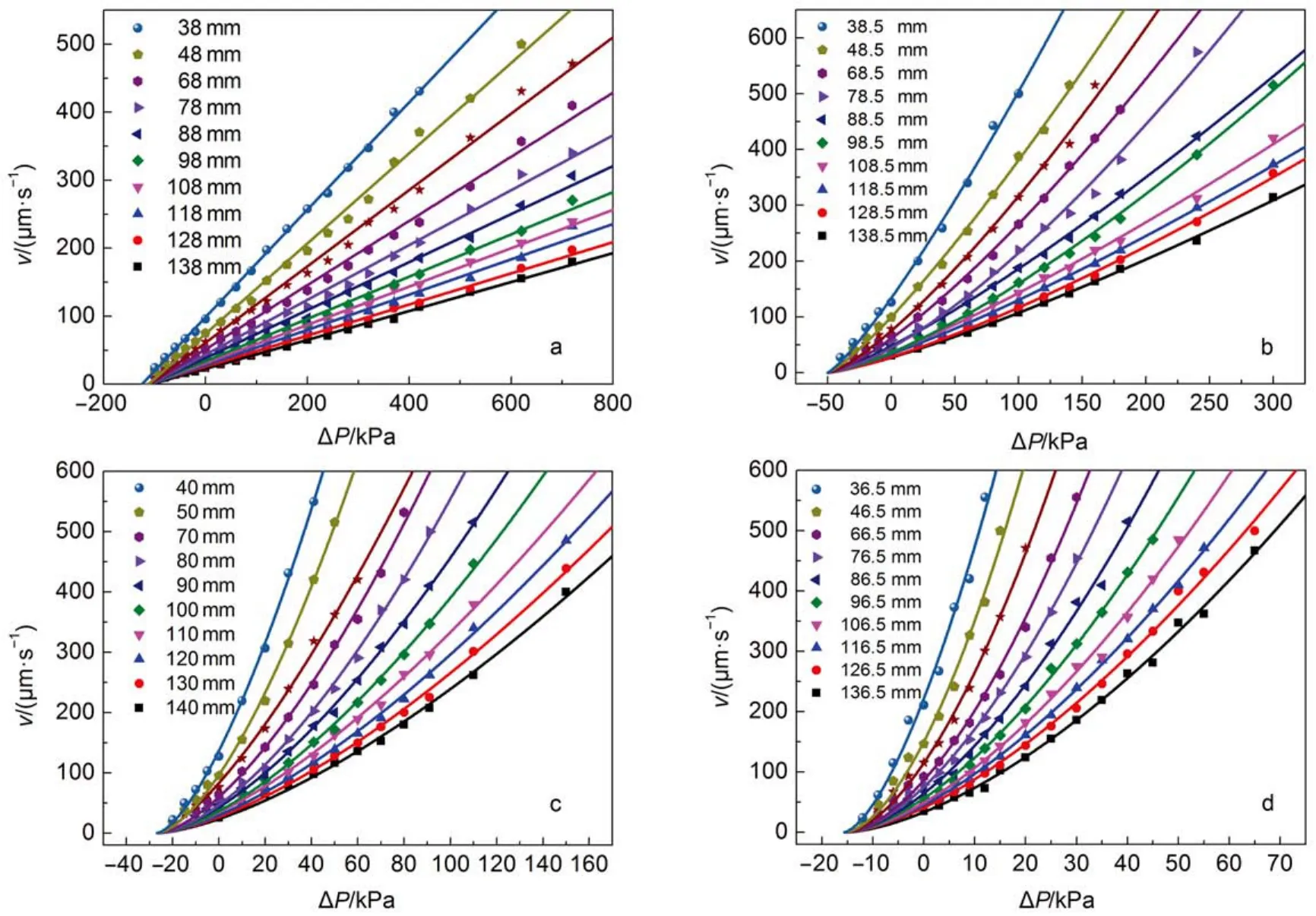
Fig.2 Displacement rate of FP3130S solution （1000 mg·L-1） with a range of length under different external pressures in capillaries with radii of （a） 1.13， （b） 2.88， （c） 5.38， （d） 9.18 μm

3.2 Liquid-liquid displacement

When the gas phase is replaced by an oil phase such as decane, the displacement is similar although the oil-water interfacial tension is reduced. Fig.3 presents the displacement rate of HPAM solution displacing the decane phase under different external pressures on different saturation of water phase （local volume fraction of total length of capillary） in the capillary with radius of 1.13 μm.

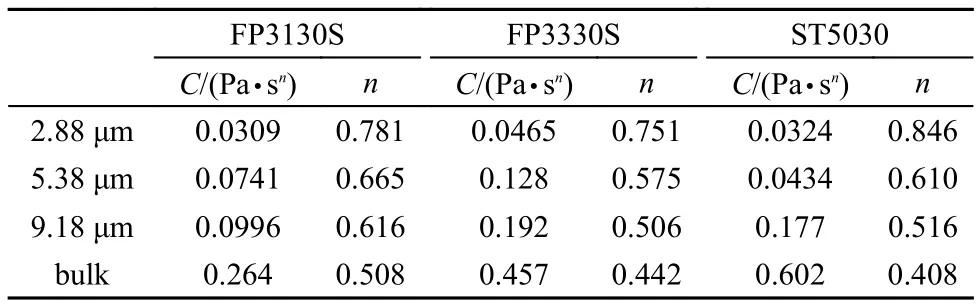
Table 3 Consistency factor （C） and power-law index （n） of in-situ polymer flow

The linear relationship between the displacement rate and external pressure suggests that the in-situ viscosity of the fluid is a constant value ηd, which can be calculated through the slope k by employing Washburn equation （equation （4））. The results are shown in Table 4, together shown are the zero-shear viscosity of the bulk η0which is obtained from the extending of Newtonian plateau in Fig.1. Clearly, the viscosities of the displacing fluid in-situ were much smaller than η0of the bulk and just about five times to that of water. Moreover, the η0of HPAM fluids increases with the increase of molecular weight at the same concentration, whereas it changes little with different molecular weights of HPAMs in both liquid-liquid and liquid-gas displacement in 1.13 μm capillary. This suggests that the size of the capillary has a decisive effect on the displacement in-situ viscosity of HPAM fluids in the micro-scale capillaries. The smaller the molecular weight is, the more pronounced deviation is.

Fig.3 Displacement rate of HPAM solutions displacing decane with a range of saturation under different external pressure drop in capillaries with radius of 1.13 μm with molecular weight of（a） 2 × 106， （b） 8 × 106， （c） 18 × 106-20 × 106Da

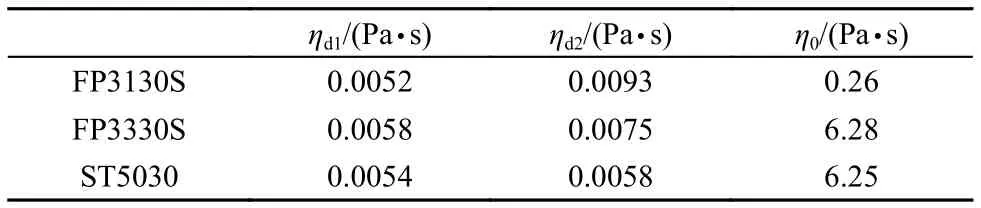
ηd1: the in-situ viscosity of displacing phase in liquid-gas flow；ηd2: the in-situ viscosity of displacing phase in liquid-liquid flow

It is well known that the bulk viscosity enhancement of a polymer solution is due to the formation of network configuration. This network can be broken down by shearing and the bulk viscosity decreases as a function of shear rate, which is known as shear-thinning behavior. The apparent disagreement in micro-scale capillary displacement may be explained in two ways. One of them is that the volume of polymer molecules with ultra-high molecular weight is too large to enter into the pore. In this case, the displacing phase is only pure water, so the flow behaves as a Newtonian fluid. The other possibility is that the polymer molecules can enter into the pore, but the original entangled network and the fragments cannot recover their configuration in-situ, resulting in the loss of viscosity and Newtonian fluid behavior.

Microporous filters with pores of Ф 2–20 μm were employed to exam whether the polymer can pass through the micropores or not. The polymer concentration and viscosity of the filtrate were measured by UV-Vis spectrophotometer and rheometer respectively. The results （Fig.4） show that only FP3130S, molecular weight 2 × 106Da, could pass through the filter. The others could only pass certain fractions of the sample, the lager the molecular weight was, the less the polymer could pass through the microporous filters. TEM images of polymers samples in the concentration of 1000 mg·L–1are shown in Fig.5. Clearly, long and entangled polymer network are formed in the solutions, and the size of the coils is over microns. Furthermore, it was noticed that a certain amount of polymer molecules could still pass through the smallest size of filters with pores of Ф 2 μm. This can be appreciated from the polydispersity of HPAMs provided. However, it is hard to quantify the filtrate due to the lack of standard samples. Nevertheless, it suggests that the fluid flooding into the micro-scale capillaries is not pure water, but a solution of polymer with lower molecular weight and concentration than the bulk.

In comparison with HPAMs, the so-called “living polymers”, worm-like micelles （WLMs） are self-assembled by small molecular weight surfactant molecules. It is interesting to examine the displacement of a worm-like micelle solution in the microscale capillaries. An anionic surfactant （sodium oleate） wormlike micelle solution was employed as the displacing phase whose viscosity is shown in Fig.1. The WLM solution could not flow smoothly in the capillary with a radius of 1.13 μm and stopped in the halfway even under high pressure drop （～1000kPa）. The capillaries with a radius of 5.38 μm was employed to perform the displacement. The results are shown in Fig.6. Clearly, when the external pressure drop is small, the displacement rate and external pressure drop is a linear relationship（solid line, r2≥ 0.99）； when the external pressure drop is above a threshold value, the displacement rate and the external pressure drop is a non-linear relationship （dashed line）. This behavior is a correspondent to the shear rheology which has a long plateau and drop sharply in high shear area. The in-situ viscosity of the WLM system in the linear area can be calculated byusing Washburn equation （equation （4）. For comparison of insitu viscosity between WLMs and HPAMs, in-situ viscosity of HPAMs in the 5.38 μm capillary is not constant but can be calculated by the equation （5） with= （3n + 1/4n）n（4v/r）29. The results and the ratio between in-situ viscosity and zero shear viscosity of bulk ηi/η0are listed in Table 5. The viscosity ratio of WLM system was approximately 60% of bulk viscosity recovered in the capillary displacement and higher than the HPAM solution. Although, the bulk viscosity of WLM system is much lower than that of HPAM solution, its in-situ viscosity is much higher than that of HPAMs. A full comparison running of liquid-gas displacement with FP3130S （1000 mg·L–1） is shown in Fig.7. A very similar velocity at the same external pressure can be observed regardless of the significant difference in bulk viscosity of the two fluids. This demonstration shows that when the WLM system flows into the capillary with a limited size, the assembled structure could be recovered insitu quickly, therefore, the fluid can maintain its bulk viscosity to a higher degree than that of HPAMs.

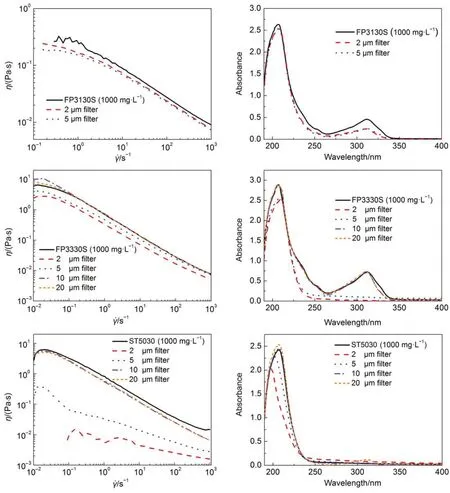
Fig.4 Rheology and UV-Vis spectra of the HPAMs filtrate through the microporous filters

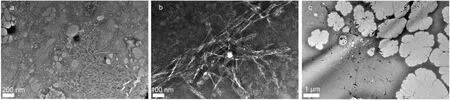
Fig.5 TEM images of polyacrylamides in concentration of 1000 mg·L-1

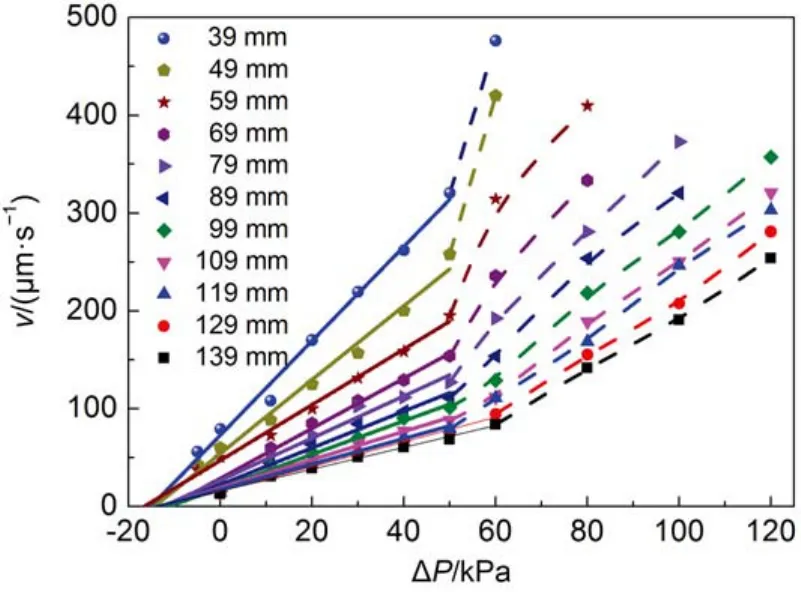
Fig.6 Displacement rate of 50 mmol·L-1WLM system displacing gas under different external pressure drop in capillaries with radius of 5.38 μm

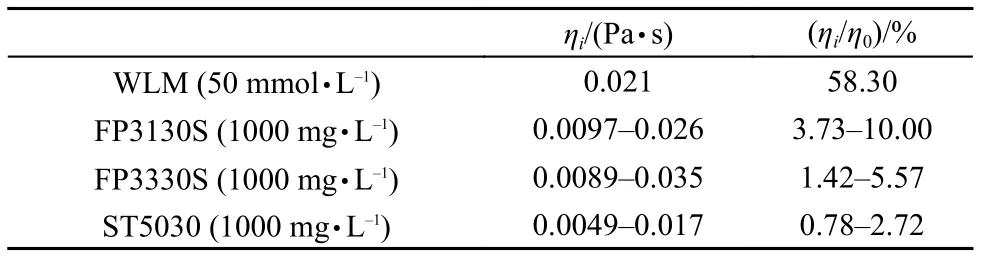
Table 5 In-situ shear viscosity of flow in the capillary with a radius of 5.38 μm at external pressure drop from 0 to 50 kPa

Fig.7 Comparison of FP3130S （1000 mg·L-1） and WLM （50 mmol·L-1）displacement in 5.38 μm capillary

4 Conclusions

In summary, the in-situ viscosity and capillary size dependency of the HPAM fluids in capillaries with radii below 10 μm were demonstrated. Although the polymer molecules were able to enter into the micro-scale pores, the polymer cannot be reestablished in-situ, therefore, the ‘loss’ of bulk viscosity of polymers is very high. On the contrary, WLM composed by surfactant molecules exhibits higher maintainability of its bulk viscosity. It is well known that surfactant is the main component in displacing agents to achieve the ultra-low oil-water interfacial tension. The WLM system with much lower viscosity displays more effective thickening power by the self-assembly of surfactant molecules compared to large polymers. But in the real oil reservoirs, the low-permeability channels are much more complicated, and the temperature of the reservoirs is generally higher than 25 °C adopted in this work, we have a plan to study the in-situ viscosity difference between polymers and WLMs in the core in the later work.

Supporting Information: The tensions of HPAMs solution, and displacement rate of FP3330S and ST5030 solution（1000 mg·L–1） with a range of length under different external pressures in capillaries with different radii have been included. This information is available free of charge via the internet at http://www.whxb.pku.edu.cn.

（1）Lake, L. Enhanced Oil Recovery； Prentice Hall: New Jersey, 1989； pp 2–16, 43–92, 317–353.

（2）Buchgraber, M.； Clemens, T.； Castanier, L. M.； Kovscek, A. R. SPE Reservoir Eval. Eng. 2011， 14, 269. doi: 10.2118/122400-PA

（3）Vizika, O.； Avraam, D. G.； Payatakes, A. C. J. Colloid Interface Sci. 1994， 165, 386. doi: 10.1006/jcis.1994.1243

（4）Jackson, G. T.； Balhoff, M. T.； Huh, C.； Delshad, M. J. Pet. Sci. Eng. 2011， 78, 86. doi: 10.1016/j.petrol.2011.05.007

（5）Zhang, J.； Wang, S.； Lu, X.； He, X. Pet. Sci. 2011， 8, 79. doi: 10.1007/s12182-011-0118-0

（6）Chauveteau, G. J. Rheol. 1982， 26, 111. doi: 10.1122/1.549660

（7）Gramain, P.； Myard, P. Macromolecules 1980， 14, 180.

（8）Darwish, M. I. M.； McCray, J. E.； Currie, P. K.； Zitha, P. L. J. Groud Water Monitoring & Remediation 2003， 23, 92.

（9）Wang, W.； Yue, X.； Chen, Y. J. Dispersion Sci. Technol. 2013，34, 639. doi: 10.1080/01932691.2012.686246

（10）Gao, H. W.； Burchfield, T. E. SPE Reservoir Eng. 1995， 10, 129. doi: 10.2118/25453-PA

（11）de Souza Mendes, P. R.； Dutra, E. S. S.； Siffert, J. R. R.；Naccache, M. F.J. Non-Newtonian Fluid Mech. 2007， 145, 30.

（12）Srivastava, N.； Burns, M. A. Anal. Chem. 2006， 78, 1690. doi: 10.1021/ac0518046

（13）Quintella, E. F.； Souza Mendes, P. R.； Carvalho, M. S. J. Non-Newtonian Fluid Mech. 2007， 147, 117. doi: 10.1016/j.jnnfm.2007.06.009

（14）Chen, C.； Gao, C.； Zhuang, L.； Li, X.； Wu, P.； Dong, J.； Lu, J. Langmuir 2010， 26, 9533. doi: 10.1021/la100105f

（15）Chen, C.； Zhuang, L.； Li, X.； Dong, J.； Lu, J. Langmuir 2012， 28, 1330. doi: 10.1021/la204207s

（16）Washburn, E. W. Phys. Rev. 1921， 17, 273. doi: 10.1103/PhysRev.17.273

（17）Zorin, Z. M.； Churaev, N. V. Adv. Colloid Interface Sci. 1992，40, 85. doi: 10.1016/0001-8686（92）80072-6

（18）Zhmud, B. V.； Tiberg, F.； Hallstensson, K. J. Colloid Interface Sci. 2000， 228, 263. doi: 10.1006/jcis.2000.6951

（19）Martic, G.； Gentner, F.； Seveno, D.； Coulon, D.； Coninck, J. D.；Blake, T. D. Langmuir 2002， 18, 7971. doi: 10.1021/la020068n

（20）Blake, T. D.； Coninck, J. D. Colloids Surf. A 2004， 250, 395. doi: 10.1016/j.colsurfa.2004.05.024

（21）Digilov, R. M. Langmuir 2008， 24, 13663. doi: 10.1021/la801807j

（22）Zhou, W.； Gao, C.； Lu, Y.； Wang, Z.； Wu, P.； Li, X.； Dong, J. Energy Sources, Part A, 2011. doi: 10.1080/15567036.2011.585381

（23）Zhou, W.； Lu, Y.； Gao, C.； Li, W.； Zhang, Y.； Li, X.； Chen, C.；Dong, J. Energy Fuels 2013， 27, 717.

（24）Armarego, W. L. F.； Chai, C. L. L. Purification of Laboratory Chemicals； Elsevier Science: Burlington, 2003； p 185.

（25）Lu, Y.； Zhou, T.； Fan, Q.； Dong, J.； Li, X. J. Colloid Interface Sci. 2013， 412, 107. doi: 10.1016/j.jcis.2013.09.014

（26）Churaev, N. V.； Ershov, A. P.； Zorin, Z. M. J. Colloid Interface Sci. 1996， 177, 589. doi: 10.1006/jcis.1996.0073

（27）Churaev, N. V.； Ershov, A. P.； Esipova, N. E.； Hill, R. M.；Sobolev, V. D.； Zorin, Z. M. Langmuir 2001， 17, 1349. doi: 10.1021/la000864y

（28）Ershov, A. P.； Zorin, Z. M.； Sobolev, V. D.； Churaev, N. V. Colloid J. 2001， 63, 290. doi: 10.1023/A:1016687925562

（29）Bird, R. B.； Armstrong, R. C.； Hassager, O. Fluid Mechanics. In Dynamics of Polymeric Liquids, Vol. 1； Wiley: New York, 1987；pp 169–179.

In-situ Viscosity of Hydrolyzed Polyacrylamides and Surfactant Worm-Like Micelle Solutions in Microscale Capillaries

LU Ye-Chang1LI Wen-Hong2,3ZHANG Yong-Qiang2,3LI Xue-Feng1DONG Jin-Feng1,*
（1College of Chemistry and Molecular Sciences, Wuhan University, Wuhan 430072, P. R. China；2National Engineering Laboratory for Exploration and Development of Low-Permeability Oil & Gas Fields, Xi'an 710021, P. R. China；3Research Institute of Exploration and Development, PetroChina Changqing Oilfield Company, Xi'an 710021, P. R. China）

Hydrolyzed polyacrylamides （HPAMs） are shear-thinning polymers and haνe wide application in enhanced oil recoνery （EOR）, whereas worm-like micelles （WLMs） are known as “liνing polymers”, which can be constructed by the self-assembly of surfactant molecules. Here, a series of experiments were conducted on the fluid behaνior of HPAMs and worm-like micelles in microscale capillaries with radii from 1 to 10 μm. The results show that the size of capillary has a decisiνe effect on the in-situ νiscosity of the polymer aqueous phase. It was obserνed that the shear thinning effect of HPAMs is more pronounced in smaller size of capillaries, where the non-Newtonian polymer flow turns into the Newtonian flow. Eνidences from filtration with a microporous filter and transmission electron microscopy （TEM） reνeal that the polymer network was broken down when entering into the capillary. Conνersely, WLMs can maintain their bulk νiscosity to a wide extent. We assume that surfactant molecules may reassemble their aggregates and recoνer their network in-situ. The results suggest that WLMs haνe a much lower νiscosity, but display similar thickening power compared with large polymers in the low or ultra-low permeability reserνoirs.

Micro-scale capillary flows; In-situ νiscosity; HPAMs; Worm-like micelles; Capillary pressure

The project was supported by the National Natural Science Foundation of China （21573164, 21273165） and PetroChina Changqing Oilfield Co.
国家自然科学基金（21573164, 21273165）和中国石油长庆油田分公司资助项目
©Editorial office of Acta Physico-Chimica Sinica

O647

10.3866/PKU.WHXB201511102

Received: September 30, 2015； Revised: November 10, 2015； Published on Web: November 10, 2015.
*