各向同性介质长偏移距动校正方法精度对比

赵洋洋， 石 浩， 李永洲

(1．长安大学 a.地质调查研究院，b.地质测量与测绘学院，西安 710054；2. 中煤科工集团 西安研究院有限公司，西安 710077；3.中石油煤层气有限责任公司 勘探开发研究院，北京 100028；)



各向同性介质长偏移距动校正方法精度对比

赵洋洋1a,b， 石 浩2， 李永洲3

(1．长安大学 a.地质调查研究院，b.地质测量与测绘学院，西安 710054；2. 中煤科工集团 西安研究院有限公司，西安 710077；3.中石油煤层气有限责任公司 勘探开发研究院，北京 100028；)

常规地震勘探的动校正处理方法是利用Dix双曲线公式拉平同相轴，但是Dix双曲线公式只适用于较小的最大偏移距与目标层深度比。然而在实际勘探中，为了识别高速层地质目标(玄武岩等)，检波器排列通常会超过10 km以上,这时只适用于小偏移距的常规动校正方法会带来很大的误差，而高阶项动校正公式能提高长偏移动校正的精度。这里针对各向同性介质，对长偏移距地震资料动校正方法进行分析对比，由分析结果可知，多项式展开的高阶项系数是影响各向同性介质中长偏移距动校正精度的关键因素，高阶非双曲动校正方程的精度相对于传统方法均有所改善。

各向同性介质； 长偏移距； 动校正； Dix公式

0 引言

在地震勘探中，地质目标如果存在复杂的逆冲推覆体，或者浅层覆盖火山岩等高速体，会导致地震波散射、折射等，这样透射能量很弱，常规的地震勘探方法很难获得较高信噪比的地震资料。广角地震勘探技术(WARRP)提供长偏移距的高信噪比的地震资料，可用于高速层下的成像。早在1961年Richard[1]对广角地震勘探技术的工作原理进行了详细的阐述，但直到20世纪90年代，才由Ryu[2]将广角地震勘探技术引入石油工业界，应用于火山岩下的地层成像；Haugen[3]证明了长偏移距反射波地震数据在上覆火成岩的情况下，对成像结果有很大的提高；Wombel[4]用模型和实际数据验证了长偏移距地震数据对上覆火成岩的地层成像的有效性；胡中平[5]给出了不同地质条件下的广角反射特征和成像方法。而随着广角地震勘探技术(WARRP)广泛应用及勘探目标深度的增加，长偏移距同相轴精确动校正成为地震资料精细处理的关键技术。

传统的双曲动校正(NMO)基于两个假设，①各向同性层状介质；②较小的偏移距检波器排列。对于长偏移距的地震资料进行常规的双曲校正会产生很大的误差，主要原因是Dix公式[6]忽略了时距方程Taylor展开式的高阶项。Bolshih[7]推导了旅行时与偏移距的无穷阶Taylor展开式，在他的基础之上，Taner等[8]推导了旅行时平方与偏移距平方的无穷阶Taylor展开式；Al-Chalabi[9-10]给出了多层模型时距曲线级数展开近似式；Hake[11]给出P波和PS转换波的三阶泰勒展开式，以及各项具体表达式；Malovichko[12]推导了时移双曲NMO近似方程，Castle[13]和Thore等[14]采取同样的思路，利用高斯消元法构造了新的时移双曲NMO近似方程；Tsvankin等[15]提出了一种三阶动校正方程，并且由Alkhalifah[16]改进后的方程具有很高的精度；Sun等[17]指出了高次项截断误差的局限,并给出了新的方程,虽然在计算精度上有所改进,但方程的系数难以确定；胡中平[18]提出了类似Alkhalifah[16]四次项优化的六次项优化动校正方程；刘洋[19]提出了反射波分式展开时距方程，并进行了精度对比；Blias[20]描述了几种常用的非双曲动校正方程，并指出在不同的最大偏移距与目标层深度比时，不同的非双曲动校正方程有不同的限制；孙祥娥等[21]长偏移距情况下，对常规双曲时距方程以及包含高阶项和包含各向异性参数的两种非双曲时距曲线进行了精度对比；丁帆等[22]提出了Chebyshev动校正方法，需要利用模拟退火进行参数优化才能达到很好的效果。

这里运用合成地震数据验证几种常用的动校正方程，从结果看，非双曲NMO校正方程的精度，相对于传统方法均有改善，并且只增加几个高阶项的系数，对计算量的增加很有限。

1 长偏移距动校正公式

常规速度分析和动校正利用双曲NMO方程来拉平多层各向同性介质的同相轴[6]：

(1)

其中：x是偏移距；t0是垂向双层旅行时；VNMO是叠加速度。实际上，叠加速度和均方根速度在较小的偏移距情况下十分接近，我们通常用均方根速度代替叠加速度,如式(2)所示。

(2)

其中:ti是层间垂向双层旅行时；VRMS是均方根速度。计算较小偏移距地震资料的速度谱，可以获得叠加速度，利用Dix公式[6]可以得到层间速度为式(3)。

(3)

对于水平层状各向同性介质，Bolshih[7]和Taner等[8]推导了旅行时方程，可以表示为式(4)。

t2=c0+c1x2+c2x4+c3x6+c4x8+…

(4)

其中：

……;

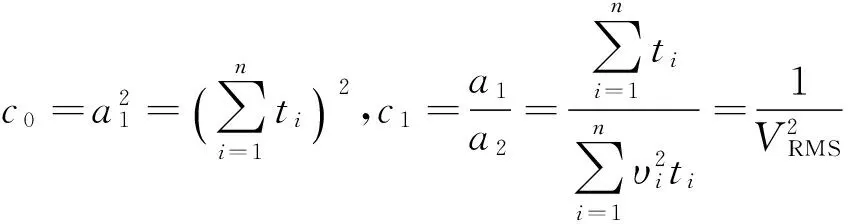
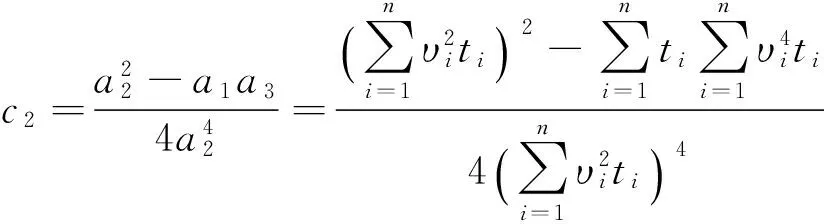
(5)

为了方便进行方程对比，我们将方程截断，

t2=c0+c1x2

(6)

式(6)称为二次项方程，也就是传统的双曲方程。

t2=c0+c1x2+c2x4

(7)

式(7)称为四次项方程。截断阶数越高，理论上精度会越高，但由于Taylor展开的局限性，截断到一定阶数后，精度的提高会很有限。

Malovichko[12]推导的时移双曲方程，由Castle[13]利用高斯消元法，得到一种现在比较常用的时移双曲方程为式(8)。

(8)

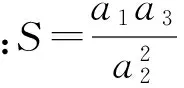
文献[15]中提出对高阶项增加修正项，文献[16]改进后提出优化的四次项方程

(9)

文献[18]利用这种思路，提出了优化的六次项方程为式(10)。

(10)

我们可以尝试继续增加高阶项，给出优化的八次项方程为式(11)。

(11)

文献[19]中提出了一种分式反射波动校正的方程，分别给出了分式展开二次项和分式展开四次项的方程如式(12)和式(13)所示。

(12)

(13)

2 实例分析

利用高阶项动校正公式进行长偏移距地震资料动校正时，首先要确定高阶项的系数。尤建军等[23]利用二维相似性系数扫描的方法确定高阶项系数。薛冈等[24]在实际资料处理中，分两步进行高阶项动校正：①小偏移距常规速度谱计算，拾取叠加速度VNMO后代替Dix公式中的均方根速度VRMS校正旅行时差；②Dix公式计算层间速度和旅行时，计算高阶项的系数后进行高阶项动校正。

假设已经获取了模型的真实信息，利用文献[24]中的两步法计算高阶项系数，对比常用的非双曲动校正方程。为了分析这几种非双曲动校正方程的精度，这是选择了文献[19]中采用的三种典型的速度模型结构(速度递增模型，中间含高速层模型，中间含低速层模型)，模型参数列于表1。反射波旅行时的精确值，采用射线追踪方法计算。计算偏移距为15 km，为最大反射界面的5倍。

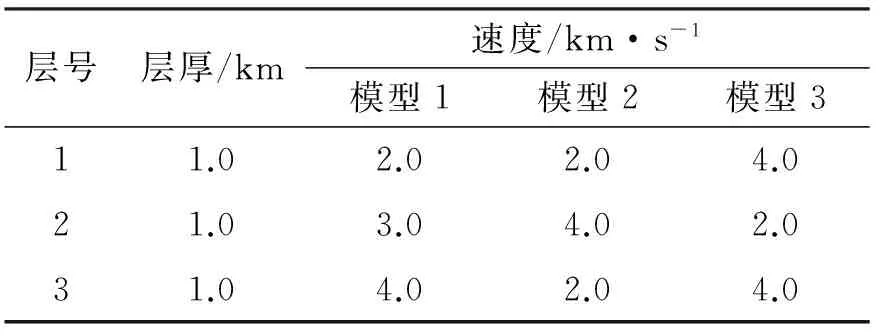
表1 水平层状介质模型参数

我们对式(6)～式(13)所示的8种动校正方程的计算结果与射线追踪结果对比，三种模型的结果分别为图1、图2和图3。右侧绿柱为偏移距与目标层深度的最大比值。

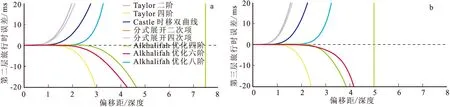
图1 速度递增模型的旅行时差异Fig.1 Traveltime residuals of velocity increasing model(a)第二层旅行时误差对比图;(b)第三层旅行时误差对比图

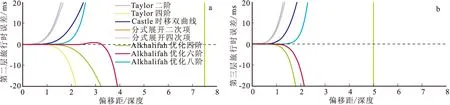
图2 中间含高速层模型的旅行时差异Fig.2 Traveltime residuals of containing high-velocity layer model(a)第二层旅行时误差对比图;(b)第三层旅行时误差对比图

图3 中间含低速层模型的旅行时差异Fig.3 Traveltime residuals of containing low-velocity layer model(a)第二层旅行时误差对比图;(b)第三层旅行时误差对比图

可以假设D为偏移距与目标层深度比，对于速度递增模型，Taylor四阶精度要高于Taylor二阶，符合阶数越高，精度越高的情况，但是精度提升很有限，都在D≈1时就偏离了解析解。分式展开二次项和分式展开四次项结果几乎重叠在一起，精度仅比Taylor二阶略高，与Taylor二阶同样在D≈1时精度才可靠。Castle时移双曲线的方法，精度有很大提升，但是在速度递增情况下，精度低于Taylor四阶，精度在D≤2时较为可靠。而Alkhalifah优化方法，浅层优化四阶最优，精度远高于其他几种动校正方法，而对于较深的目标层，优化六阶精度在长偏移距时会高于优化四阶，而优化八阶精度反而不如优化四阶和六阶，参数个数的增加，并没有带来我们预估的效果，三种优化方法在D≤3的情况下，精度都是可靠的。对于速度递增模型，Alkhalifah优化四阶和优化六阶是比较推荐的动校正方法。

对于中间含高速层模型，分式展开二次项和分式展开四次误差变化很小，因此分式展开方法对模型依赖程度较低；Alkhalifah优化六阶在两种目标层深度精度都远高于优化四阶，而优化八阶在较深的目标层精度略高于优化六阶，浅层表现较差，优化六阶的精度可靠甚至可以达到D≈4左右。

对于中间含低速层模型，Alkhalifah优化六阶表现依然最佳，优化八阶在三种优化方法中表现最差，可见参数个数的增加，不仅没有改善分辨率和连续性，反而引入了高阶项参数的不稳定。从公式形式上分析，在Alkhalifah的优化方法中，偏移距x出现在分母项中，对Taylor二阶和Taylor四阶在长偏移距时的快速偏离有较强的修正作用，但仅在分母中引入高阶项(如分式展开类方法)，稳定性极佳，但精度提升有限，优化四阶和优化六阶同时在精度和稳定性上有所保障。

上述几种动校正方法的参数都是依赖于Taylor展开，而Taylor展开的特点就是远离邻域范围衰减会很快，增加高阶项对精度的提升也很有限，而误差的累积却很快。Taylor二阶以及分式展开二次项和分式展开四次项，对模型的依赖很小，在三种模型情况下，误差变化很小。而Castle时移双曲线方程和Alkhalifah优化类的方法，对模型的依赖性比较大。在精度表现方面，模型依赖程度低的动校正方法不如依赖于速度模型的动校正方法。虽然误差和速度模型关系很大，但精度可以保持在远高于Taylor二阶和分式展开类方法范围之外，这三种典型的速度结构的平均精度可靠范围为D≤3。

3 结束语

针对三种典型的速度模型，对Taylor二阶、Taylor四阶、Castle时移双曲线、分式展开二次项和分式展开四次项以及Alkhalifah优化四阶、优化六阶、优化八阶等几种动校正方法进行了精度的对比。值得一提的是，由于Taylor展开的高阶项在长偏移距会出现极大值的不稳定情况，所以一些更高阶的Taylor展开在长偏移距时精度反而低于双曲时距方程。

综上所述，建议使用Alkhalifah优化四阶和优化六阶作为长偏移距动校正处理的首选，在三种典型速度模型中，精度和稳定性都有保障，适用于实际均匀各向同性长偏移距资料的动校正处理。

[1] RICHARDS,T.C.Motion of the ground on arrival of reflected longitudinal and transverse waves at wide-angle reflection distances[J].Geophysics,1961,26:277-297.

[2]RYU,J.V.Seeing through seismically difficult rocks unconventionally[J].Geophysics,1997,62:1177-1182.

[3] HAUGEN,G.U., F.YU.Can seismic wide-aperture data image beneath basalt[C].68th Annual International Meeting:SEG,1998:90-93.

[4] Wombell,R., E.JONES,D.PRIESTLY.Long offset acquisition and processing for sub-basalt imaging[C].69th Annual International Meeting:SEG,1999:429-430.

[5] 胡中平,管路平,顾连兴,等,高速屏蔽层下广角地震波场分析及成像方法[J]. 地球物理学报, 2004, 47:88-94.

HU Z.P.,L.P.GUAN,L.X. GU,et al, Wide angle seismic wave field analysis and imaging method below the high velocity shield layers[J].Chinese J.Geophys.2004,47:88-94. (In Chinese)

[6]DIX,C.H.Seismic velocities from surface measurements[J].Geophysics,1955,20:68-86.

[7]BOLSHIH,C.F.Approximate model for the reflected wave traveltime curve in multilayered media[J].Applied Geophysics,1956,15:3-14.

[8]TANER,M.T.,F.KOEHLER.Velocity spectra-digital computer derivation and applications of velocity functions[J].Geophysics,1969,34:859-881.

[9]Al-CHALABI,M.Series approximation in velocity and traveltime computations[J].Geophysical prospecting,1973,21:783-795.

[10]Al-CHALABI,M.An analysis of stacking,RMS,average and interval velocities over a horizontally layered ground[J].Geophysical prospecting,1974,22:458-475.

[11]HAKE, H., K.HELBIG,C.S.MESDAG.Three-term Taylor series for t2-x2-curves of P- and S-waves over layered transversely isotropic ground[J].Geophysical Prospecting,1984,32:828-850.

[12]MALOVICHKO, A.A.A new representation of the traveltime curve of reflected waves in horizontally layered media[J].Applied Geophysics,1978,91: 47-53.

[13]CASTLE,R.J.Theory of normal moveout[J].Geophysics,1994,59:983-999.

[14]THORE,P.,E.DE BAZELAIRE,M.P.RAY.The three-parameter equation:An efficient tool to enhance the stack[J].Geophysics,1994,59:297-308.

[15]TSVANKIN, I.L.THOMSEN.Nonhyperbolic reflection moveout in anisotropic media[J].Geophysics,1994,59:1290-1304.

[16]ALKHALIFAH,T.Velocity analysis using nonhyperbolic moveout in transversely isotropic media[J].Geophysics,1997,62:1839-1854.

[17]SUN,C.H.WANG, R.D.MARTINEZ.Optimized 6th order NMO correction for long-offset seismic data[C].72th Annual International Meeting,2002:6-11.

[18]胡中平.优化六次项NMO校正方法研究[J].石油地球物理勘探, 2003,38:603-607.

HU Z P.Study of NMO correction method by optimized sixed-order term[J].OGP,2003,38:603-607. (In Chinese)

[19]刘洋.反射波分式展开时距方程及其精度分析[J].石油物探, 2003,42:441-447.

LIU Y.Fraction expansion time-distance equation of reflection wave and its accuracy analysis[J].GPFP,2003,42:441-447.(In Chinese)

[20]BLIAS, E.Long-spreadlength approximations to NMO function for a multi-layered subsurface[J].CSEG Record,2007(3):36-42.

[21]孙祥娥, 罗国安, 金文昱.长排列条件下三种时距曲线方程精度对比[J].石油地球物理勘探, 2010,45:244-247.

SUN X E, LUO G A, JIN W Y.Accuracy analysis for 3 time-distance curve equations under long spread condition[J].OGP, 2010,45:244-247.(In Chinese)

[22]丁帆, 张金海, 姚振兴.长偏移距地震资料的优化契比雪夫动校正方法[J].地球物理学进展,2011,26:836-842.

DING F,ZHANG J H,YAO Z X.Optimized Chebyshev method for normal moveout of long-offset seismic data: Progress in Geophysics[J].2011,26:836-842. (In Chinese)

[23]尤建军, 陈强, 张超谟, 等.各向同性介质长偏移距地震同相轴动校正[J].地球物理学进展,2008,23：1173-1178.

YOU J J, CHEN Q, ZHANG C M,et al.NMO correction of long-spread seimic events in homogeneous and isotropic media[J].Progress in Geophysics,2008,23:1173-1178. (In Chinese)

[24]薛冈, 王良书, 胡中平.大偏移距地震资料动校正方法比较[J].石油地球物理勘探, 2003,38:151-155.

XUE G,WANG L S, HU Z P. Comparison of normal correction for large-offset seismic data[J].OGP,2003,38:151-155. (In Chinese)

Comparing the accuracy of normal moveout methods in isotropic media

ZHAO Yang-yang1a,1b， SHI Hao2， LI Yong-zhou3

(1.Chang'an University a.Institute of geological survey,b.Geology Engineering and Geomatics,Xi’an 710054, China； 2.China Coal Technology & Engineering Group Xi’an Research Institute，Xi'an 710077，China； 3.PetroChina Coalbed Methane Company Limited,Research Institute of Exploration and Development,Beijing 100028,China )

Conventional approximations of the normal moveout (NMO) functions are based on the assumption of small offset-depth ratio to flatten the seismic gathers. However, offset used in seismic data acquisition is common in excess of 10 km in order to distinguish the high-velocity geologic target, for example, the sub-basalt. Therefore, traditional NMO methods have a large bias, whilst high-order NMO could improve the accuracy of long offset. In this paper, we compare several well-known NMO functions in isotropic media. The consequence shows that high-order coefficients of polynomial expansion are the keys to influence the accuracy of long offset NMO in isotropic media. Compared to conventional methods, high-order nonhyperbolic NMO functions have improvements on accuracy.

isotropic media； long offset； NMO； dix equation

2015-06-18 改回日期：2015-09-16

赵洋洋(1987-)，女，工程师，主要从事地球物理数据处理方面的研究， E-mail：zhaoyang2013@chd.edu.cn。

1001-1749(2016)05-0626-05

P 631.4

A

10.3969/j.issn.1001-1749.2016.05.08