面向智能导览的个性化线路规划研究
王艳,黄开建,孙茂圣,李开荣,朱俊武,3
(1.徐州工程学院信息化中心,江苏 徐州 221018;2.扬州大学信息工程学院,江苏 扬州 225127;3.圭尔夫大学计算机科学工程系,加拿大 安大略 圭尔夫 N1G2K8)
面向智能导览的个性化线路规划研究
王艳1,黄开建2,孙茂圣2,李开荣2,朱俊武2,3
(1.徐州工程学院信息化中心,江苏徐州221018;2.扬州大学信息工程学院,江苏扬州225127;3.圭尔夫大学计算机科学工程系,加拿大安大略圭尔夫N1G2K8)
个性化游览线路的规划是智能导览的核心问题之一,景区及景点信息的形式化表示是个性化游览线路自动规划的基础。针对导览线路的自动规划问题,提出一种基于无向图及H-RVT表的、带用户偏好表示的导览线路生成方法。在问题约束及影响因素分析的基础上,首先给出了景区及景点的有向图表示,进而提出基于最大相对价值表的景点信息表示方法,最后给出一种综合考虑起点与终点选择、景点选择和游览时间控制的个性化游览线路自动规划方法。该方法解决了景区、景点及路线生成的形式化表示问题,为路线规划的实现提供了理论支撑。
智慧旅游;导览;线路规划;个性化游览线路
0 引言
智能导览是智慧旅游研究与建设的关键内容之一,也是物联网技术的重要应用[1-2]。参观游览路线是否科学合理在很大程度上影响到整个游览过程的用户体验。对游客而言,科学合理的游览路线能够使其在较短的时间、较小的路程代价下获得较好的游览体验,同时,对旅游服务提供者来说,高效的游览路线也能使得相同服务资源代价的情况下获得游客更高的服务评价,从而促进旅游及其服务业的健康持续发展和进步[3-4]。
实际情况下,游客的游览时间有限,不足以完整地游览当前景区中所有的景点。游客的真实需求是在有限的时间内个性化地对当前景区内景点进行游览。因此,如何安排游览路线,成为智能导览系统中急需解决的一大问题,生成的游览路线是否可行有效且满足游客的偏好,对用户体验至关重要。
游览路线的规划设计工作本质是依据游客当前的位置信息和待参观的景区景点信息,根据一定的策略筛选合适的路线和景点,并将之有序排列在具体游览行程路线的过程中。完整的游览路线应当包括起点、景点集合、景点间的路径集合以及终点。因此,对景区内最佳游览路线问题模型的建立以及路线生成策略的设计是决定游览路线优劣程度的关键所在。
面向智能导览的个性化线路自动规划本质上是解决在有限约束下的最短路径应用问题,它是运筹学、地理信息学以及计算机网络等学科中的研究热点,比如求单源且无负边权的“一对多”的Dijkstra算法[5]、用于求多源且无负权边的“一对一”最短路径的Floyd算法[6]、求多个备选优化路径的K最短路径算法[7]以及静态路网中较为有效的“直接搜索”A*算法[8]等。同时,随着经典图论和计算机数据结构的有效结合,使得各类最短路径算法不断涌现以解决不同特征的实际问题,它们在时间复杂度、空间复杂度、应用范围以及易实现等性能上各具特色[9-10]。国内有学者专门就最短路径算法的分类体系以及研究进展[11]方面进行过较为全面的总结与研究分析。文献[12]提出了一种利用线图以及顶点赋权图的最优完全子图的方案解决中国邮递员问题中如何生成最优邮递路线的问题。该方法与通常图的相关概念的区别在于其为图中的节点(也称顶点)赋加了权值,最终求出一条能访问到图中所有节点且具有最小权值的环游。文献[13]提出了一种解决图中受K顶点数限制的所有最短路径BCSP算法以及其改进的ICSP算法,运用图的广度遍历算法以及逆邻接表、指针等数据结构知识生成扩展最短路径树。
1 问题背景
在游览过程中,以有限的时间条件为前提,从游客需求的角度出发,有如下三点直观的要求:优先参观景区内游览价值大的景点;要求所步行的路程最少,即花费在步行过程中的时间短;在不超出限定时间的前提下,尽可能充分地利用限定的时间。
以现实中大量游客对景区的参观游览行为过程的总结为基础,描述游客游览某一景区的一般活动流程为:
Step1:根据当前的位置寻找到该景区最近的入口,从入口处进入景区。
Step2:若游览时间足够长,则从当前位置开始按距离的远近开始按序游览景区内景点,直至景区内所有景点都游览完毕,结束游览活动。若时间有限,不能完整游览整个景区内所有景点,则执行Step3。
Step3:以当前位置为参考,在限定时间内,选择相对游览价值最高的未被游览的景点(即该景点知名度高且对其进行游览花费时间少)。
Step4:步行到达待参观的景点并花费一定时间完成对该景点的参观。此时,检查剩余时间是否可继续游览活动。若剩余时间可继续游览活动,则返回Step3,若剩余时间无法满足继续游览要求,则执行Step5。
Step5:从当前景点位置行至距离最近的景区出口,离开景区结束对该景区内景点的游览,完成本次游览活动。
因此,解决最佳游览路线生成问题需要完成工作为:
(1)寻找或设计最短路径算法,以无向图中任意某一节点为起点,根据其余节点的权值、价值以及该节点与其余各节点之间的最短路径,得到在当前位置状态下,满足时间限制条件的最佳下一个待游览节点。
(2)当需要游览的节点集合选定之后,在无向图G中根据边信息以及边的权值数据确定最佳的游览路线,生成选定节点集合中节点的最终游览序列。
2 景区模型抽象与景点属性表示
2.1建立无向图处理模型
旅游景区由多个出入口、内部景点集、公共服务点及内部相互之间的路径组成,游览路线的生成工作即根据约束条件按序选择合适的景点集合与路径集合。本文以无向图作为景区及景点的表示模型,将景区相关信息抽象成如图1所示附加节点值的带边权的无向图模型。

图1 某景区建立的无向图问题模型
由图1可知,将某景区的平面示意图转换为无向图G,将景区中的景点以及出入口转换为无向图G中的顶点,景点之间的路径转换为无向图中的边。
定义1:无向图G由一个二元组V,E组成,其中集合V称为无向图G的节点集合,记为,V中每个元素对应代表实际景区中一个景点;集合G称为无向图G的边集,是由集合V中的元素组成的无序对组成,记为E中每个元素表示实际情况下景区景点之间的一条路径。
这里需要注意的是边集E中元素(vi,vj)是无序对,因此无序对(vi,vj)与(vj,vi)表示的是同一条边ei,j,在集合E中只出现一次。
定义5:px(vi,vj)={ei,m,em,n,…,ek,j},(ei,m,em,n,…,ek,j∈E,x∈Ζ*)表示从节点vi出发到达节点vj的第x条路径,该路径由边ei,m,em,n,…,ek,j顺序构成。在一般情况下,节点vi到节点vj的路径并不是惟一的,定义Pji={p0(vi,vj),p1(vi,vj),…,pk(vi,vj)},k∈N*表示节点vi到节点vj的所有不同路径的集合。
2.2景点信息表示策略
2.2.1节点相对价值
在无向图G中,以vi为起点,vj为终点的一条路径px(vi,vj)的定义,以及该路径的路径代价W[px(vi,vj)]的定义。一般情况下,从节点vi出发到节点vj的路径并不惟一,并且不同的路径代价一般各不相同。根据每条路径的路径代价大小,节点vi到节点vj的所有路径的集合中必定存在一条路径代价最小的路径。
定义7:设路径p0(vi,vj)称为无向图G中,节点vi到节点vj的最短路径,该路径需要满足:
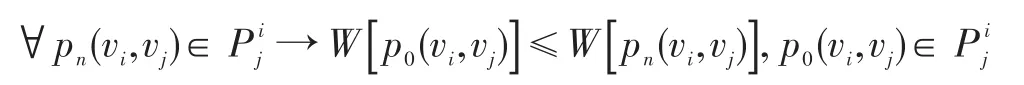
即在节点vi到节点vj的路径集合中,p0(vi,vj)的路径代价不大于该路径集合中的其余所有路径的路径代价。
在参观时间有限的条件下,从景点A出发前往景点B进行参观游览时,“景点之间路径长度”、“景点自身固有游览价值”、“景点的游览时间”这三个因素影响游客游览体验值。
在实际情况中,某一景点的实际游览价值并不是绝对的,而是相对的,其受到多个因素的影响,因而衡量该景点的实际游览价值需要综合考虑这些不同的因素。在本文中,根据前面的分析,将三个因素纳入算法计算中来衡量景点的实际游览价值。
定义8:H-rv(vi,vj)称为以节点vi为起点的,目标节点vj的最大相对价值,简称相对价值:
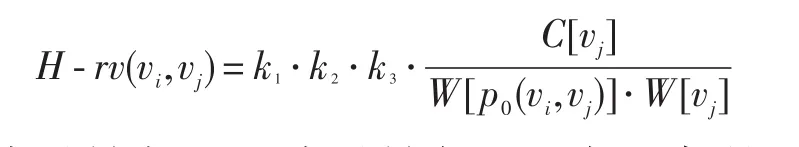
式中:vi表示景点A,vj表示景点B,vi与vj都是无向图G中的节点;k1∈R*;k2∈R*;k3∈R*;它们值的大小分别代表对应因素对景点相对游览价值影响程度的大小。
命题1:景点B的相对游览价值与景点A,B之间的路径长度成反比关系,即:

证明:设以节点vi为起点,节点vj为终点存在两条路径p1(vi,vj),p2(vi,vj),节点vj的本身固有价值为C[vj],则分别以上述两条路径从vi到vj进行游览时的价值比为:

即与节点vi到节点vj的路径长度成反比。现实意义为:参观同一个景点,步行时间代价越小,对游客而言其价值越高。
命题2:景点B的相对游览价值与景点B自身的固有游览价值成正比关系,即:

证明:设节点vj与节点vl的游览时间相等,即W[vj]=W[vl],且从节点vi出发到达节点vj、节点vl的路径时间代价相等,即W[p(vi,vj)]=W[p(vi,vl)]。从节点vi出发分别对节点vj、节点vl进行游览时的价值比为:即与节点自身的固有游览价值成正比。现实意义为:花费相同的时间代价对景点参观,所选景点本身价值越高,对游客而言其越值得游览。
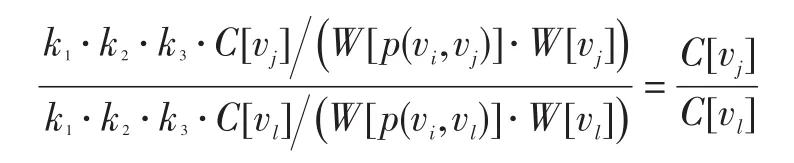
命题3:景点B的相对游览价值与景点B的游览时间成反比关系,即:
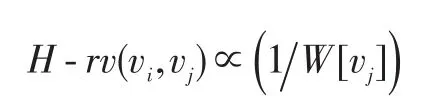
证明:设节点vj与节点vl的自身固有游览价值相等,即C[vj]=C[vl],且从节点vi出发到达节点vj、节点vl的路径时间代价相等,即W[p(vi,vj)]=W[p(vi,vl)]。从节点vi出发分别对节点vj、节点vl进行游览时的价值比为:

即与节点游览时间代价成反比。现实意义为:花费相同的路程时间代价去游览自身固有价值相同的景点,则花费在对景点的参观上的时间越少,越有益于游览游客的整体游览活动。
2.2.2节点H-RVT表定义
在最佳路径的生成过程中,以节点vi为起点选择下一个节点加入到路径中时,需要比较图中所有未被加入到路径中的节点以确保被选中的节点是当前相对价值最大的,因此需要得到以节点vi为起点到图G中其余所有节点的相对价值。
定义9:称H-RVT(vi)为节点vi的最大相对价值表(Highest-Relative Value Table),表中包含以vi为起点到图中其他所有节点相对价值,相对价值表的定义式如下:
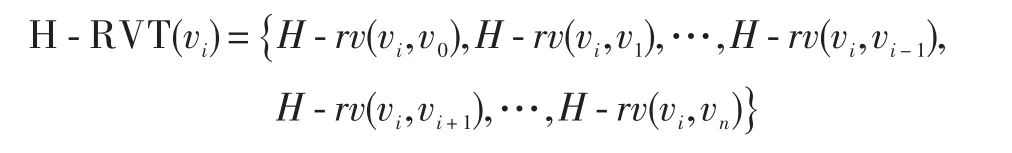
式中:n∈N;vn∈V。
表1为节点vi的相对价值表H-RVT(vi)中所包含的信息。
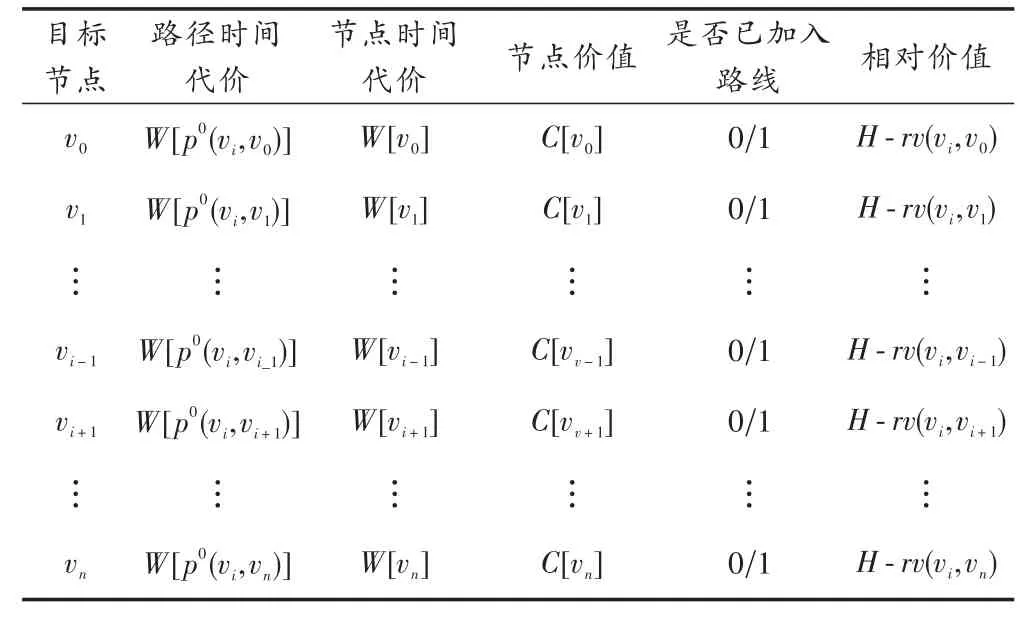
表1 节点vi的相对价值表
对表1的几点说明:
(1)目标节点表示以节点vi为起点出发需要达到的节点。节点vi的相对价值表中目标节点中包含无向图G中除vi以外的所有节点。
(2)路径时间代价表示vi与目标节点之间最短路径之中所有路径的权值之和,即从vi出发达到目标节点过程中经过的路径所用的路程时间。
(3)节点时间代价表示目标节点的时间代价,即游览目标节点对应景点所需要的时间。
(4)节点价值表示目标节点的价值,为目标节点对应景点的自身固有价值。
(5)是否已加入路线标记目标节点,是否已经被加入到最佳路线中,1代表该目标节点已加入到最佳路线中,0代表未加入。
(6)最大相对价值表示目标节点在以vi为起点的情况下的最大相对价值。在最佳路线的生成过程中,优先选择表H-RVT(vi)中相对价值高的目标节点加入到最佳路线中。
在表示景点和路径信息的无向图G中,所有节点都有其最大相对价值表,每一张表中都包含了以该节点为起点,到其他所有节点的最大相对价值。
3 条件约束与个性化路线生成
游览时间分为路程中花费的时间以及对景点进行参观游览花费的时间,游览价值取决于路线中所有景点的价值高低。从宏观上描述最佳游览路线的要求为“在限定的时间内,最高效地利用有限的时间,寻找游览价值最高游览路线”;从路线生成过程中描述最佳游览路线的要求为“保证每次加入到游览路线中的景点都是当前条件下最值得游览的景点”。
在给出最佳路线生成算法之前,先给出下列描述:
集合Vα表示无向图G中一个或者多个特定节点的集合,这类节点在实际问题中代表景区的出入口,即“出入口节点”;集合Vβ表示无向图G中除“出入口节点”以外,其余所有节点的集合,这些节点在实际问题中代表景区内的各个景点,即“景点节点”。
由Vα集合与Vβ集合的定义可知以下关系:
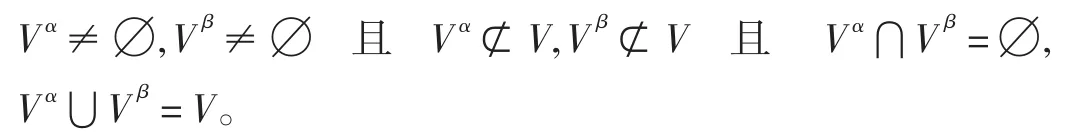
集合V0表示未加入到最佳路线中的“景点节点”的集合,初始时,V0=Vβ;
集合V*表示未加入到最佳路线中,但最佳路线需要“经过”节点的集合,初始时V*为空集。例如从景点A要去游览景点D,景点A与D之间的最短路径需要经过景点B与C,则就将景点B与C所对应的节点加入到集合V*中。
(1)其中vi∈Vα称为起点,vm∈Vα称为终点,这两个节点为“出入口节点”;路线中除起点与终点以外的节点都属于集合Vβ,这些节点为“景点节点”。
(2)在该路线中的任一节点vi的前一节点称为该节点的父节点f(vi),后一节点称为该节点的子节点S(vi),其中起点没有父节点,终点没有子节点,其余节点都有各自的父节点与子节点。例如在上述路线中,节点vn的父节点f(vn)为vl,子节点s(vn)为vp。
最佳路线生成方案的描述分为四个部分,路线起点的选择、“景点节点”选择、时间的控制、路线终点选择。
3.1路线起点选择
路线的起点为无向图G中“出入口节点”中的某一节点,起点的确定方式分为两种:第一种为指定路线起点;第二种为根据实时定位结果选择距离最近的出入口作为路线起点。“景点节点”选择(设下一个被加入到最佳路线中的节点为vnext,简称为待节点;称最佳路线中最后一个“景点节点”为该路线尾节点,设为vlast):
在景区的多个景点中选择满足一定条件的景点进行游览是游览路线生成过程中最主要的工作内容。在无向图模型的最佳路线生成过程中,每一步选择加入到最佳路线中的vnext节点都是未加入最佳路线的节点集合中选取且是这些节点中给最佳路线带来最大“效益”的一个(以benefit来表示“效益”),因此vnext有必定为以下两个节点中的其中一个:
(1)vnext是以最佳路线的尾节点为父节点,当vnext加入到最佳路线中后,将取代其父节点成为新的尾节点,即vnext是从尾节点的H-RVT(vlast)表中选取的未加入最佳路线且相对价值最大的节点。此节点加入到最佳路线带来的“效益”等于H-RVT(vlast)表中该节点的相对价值。

(2)vnext是最佳路线的路线过程中所“经过”节点中给最佳路线带来“效益”最大的一个,即vnext∈V*且满足
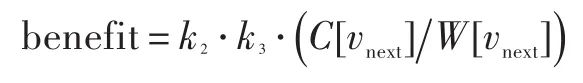
这里因为最佳路线已经“经过”该节点,所以不需要再重复考虑该节点的加入产生的路径代价
3.2时间控制
在游览路线生成的过程中,是以限定的时间T为控制条件的,整个游览过程总的耗时不能超过限定时间T,因此,在生成最佳游览路线时,每加入一个新的节点,都需要考虑该节点加入路线之后,路线增加的时间代价是否超出时间限制条件。
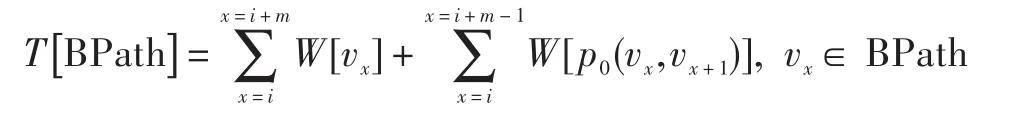
加入新的节点vnext之后,需要判定时间条件满足:
(1)当vnext是以BPath的尾节点为父节点时,增加的时间分为两个部分,到达vnext的路径所需要的时间以及vnext自身时间代价的增加,因此判断时间的依据如下:
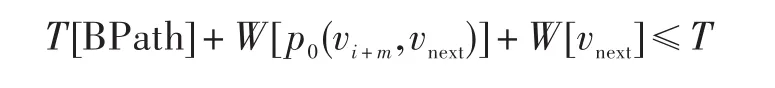
(2)当vnext是路线BPath所“经过”的节点之一时,因为该节点已经在BPath的行程中,增加的时间只是vnext自身的时间代价,因此判断时间的依据如下:
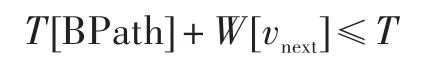
3.3路线终点选择
生成最佳路线的整个流程,首先生成最佳路线的起点,也就是选择进入景区的入口;第二步是生成最佳游览路线的主要内容,不断的在为图中未加入最佳路线的节点集合中按照加入之后的“效益”大小的顺序以及是否满足时间限制条件来选择下一个最值得加入路线;当图中未加入最佳路线的节点集合中没有满足时间限制条件的节点时,为最佳路线按照选择终点,即选择离开景区的出口,生成完整的最佳路线并输出结果。
4 结论
本文针对在有限时间生成最佳游览路线的问题,从游客的实际需求分析着手,设计了使用无向图数学模型,总结出在时间限定条件下影响景点与路径选择的三个主要因素,并根据分析结果为每个节点生成各自HRVT表,从而成功实现了生成最佳的游览路线。
[1]OWAIED H H,FARHAN H A,AL-HAWAMDEH N,et al.A model for intelligent tourism guide system[J].Journal of applied sciences,2011,11(2):342-347.
[2]GAVALAS Damianos,KENTERIS Michael.A web-based pervasive recommendation system for mobile tourist guide[J].Personal and ubiquitous computing,2011,15(7):759-770.
[3]廖川荣.校园最佳游览路线问题的数学模型分析[J].大学数学,2012,28(6):78-82.
[4]姜西瑞.基于GPS和GSM/GPRS的定位系统的设计与实现[D].北京:中国科学院计算机技术研究所,2006.
[5]章永龙.Dijkstra最短路径算法优化[J].南昌工程学院学报,2006,25(3):30-33.
[6]赫自军,何尚录.最短路问题的Floyd算法的若干讨论[J].重庆工学院学报(自然科学版),2008,22(5):156-159.
[7]徐涛,丁晓璐,李建伏.K最短路径算法综述[J].计算机工程与设计,2013,34(11):3900-3906.
[8]刘浩,鲍远律.A*算法在矢量地图最优路径搜索中的应用[J].计算机仿真,2008,25(4):253-257.
[9]ZHAN F B,NOON C E.Shortest paths algorithms:an evaluationusingrealroadnetworks[J].Transportationscience,1998,32(1):65-73.
[10]CHERK ASSKY B V,GOLDBERG A V,DIZK T R A.Shortest paths algorithms:theory and experimental evaluation[J].Mathematical programming,1996,73(2):129-174.
[11]LU Feng.Shortest path algorithms:taxonomy and advance in research[J].ACAT geodaetica cartographica,2001,30(3):269-275.
[12]李念祖.关于中国邮递员问题的最优完全子图算法[J].上海师范大学学报(自然科学版),2006,35(4):26-29.
[13]王卫强.求图中受顶点数限制的所有最短路径的算法分析研究[D].上海:华东师范大学,2007.
Research on personalized route planning oriented to intelligent guiding to visitors
WANG Yan1,HUANG Kaijian2,SUN Maosheng2,LI Kairong2,ZHU Junwu2,3
(1.Center of Informatization,Xuzhou Institute of Technology,Xuzhou 221018,China;2.School of Information Engineering,Yangzhou University,Yangzhou 225127,China;
3.Department of Computer Science and Technology,University of Guelph,Guelph N1G2K8,Canada)
Personalized tour route planning is one of cores of intelligent guiding to visitors,and the formalizing denotation of the information of scenic regions and view spots is the fundament of personalized automatic planning of touring routes.A method of generating the route automatically is given in this paper for automatic planning of touring route based on directed graph,H-RVT and users′preference.On the basis of analyzing the related factors,a method of how to express the information of scenic regions and view spots is given in this paper.A expressive method of view spot information is proposed according to the table of maximum relative price.An automatic planning method of personalized tour route is offered,which considers the selection of start point,end point,view spots and visiting time control.The method of formal representation for scenic regions,view spots and routing generation provide a theory support for realization of route planning.
wisdom tourism;guiding to visitor;rout planning;personalized tour route
TN911-34
A
1004-373X(2016)20-0092-05
10.16652/j.issn.1004-373x.2016.20.023
2016-02-05
国家自然科学基金(61170201);江苏省前瞻性研究项目(BY2015061-06;BY2015061-08);江苏省教育厅自然科学基金(14KJB520041);扬州市协同创新项目(2014-9)
王艳(1977—),女,工程师,硕士。研究方向为人工智能及其应用。
黄开建(1990—),男,江苏扬州人,硕士研究生。主要研究方向为智能软件。
孙茂圣(1971—),男,江苏南通人,高级工程师,硕士。研究方向为云计算、语义Web等。
李开荣(1963—),男,江苏兴化人,教授。研究方向为信息管理系统等。
朱俊武(1972—),男,江苏江都人,教授,博士。研究方向为人工智能及其应用。

