动态审题：数学思维的简化、质化与活化

陶士梅+王聿松

摘 要：任何复杂繁难的题目都是由简单类型组合而成的，如何能“把深奥的问题浅显化”“把表面的问题本质化”“把单一的问题多样化”是解决问题的第一步。“动态审题”即通过动笔圈画、语言转译和联想拓展可以有效帮助学生化繁为简、透过现象看本质、推一及三，助推思维的简化、质化与活化。

关键词：动态审题;动笔圈画;语言转译;联想拓展

请看两道题目：

题目一：“甲、乙两人骑车分别从东、西两村同时出发相向而行，相遇时距中点2.4千米。已知甲的速度是乙的2倍，那么东、西两村相距多少千米？”

题目二：“快、慢两车分别长150米和200米，相向行驶在平直的轨道上。若快车上的人看见慢车驶过窗口的时间是8秒，那么慢车上的人看见快车驶过窗口的时间是多少秒？”

以上题目，学生如果只是按照常规的审题方式，基本找不到头绪，因为没有清晰的数量关系，信息要么少而简单要么多而繁杂，但是看起来都和问题之间没有关系。如何能从这些貌似“无厘头”的题目中找到突破口，把复杂繁难的题目变成简易题型是审题的重要任务。

一、动态审题的内涵

众所周知“审题”就是对题目的含义进行分析和研究，正确地理解题意，明确题目要求，从而确定答题方式。其中的关键词是“分析和研究”。可事实上很多小学生在审题时经常只是单一地读、用眼睛浏览、靠想象来整理信息，如果有思路就下笔，没有思路就放弃，尤其是面对稍微复杂一点的“变式”题目只会望而却步，根本不会分析和研究。事实上，任何复杂繁难的问题都是由若干个简单问题组合而成的，如何能让学生学会“把深奥的问题浅显化”“把现象的问题本质化”“把单一的题目类型化”是审题的重要任务。

动态审题其本质就是综合调动学生的眼、口、手、脑等多种器官的参与，通过动态作图、动态转译和动态联想把数学信息明朗化、数学语言简易化、单一题型多样化，从而降低题目难度，实现简易解题。这里的“动态”有三层意思：一是让学生在审题的时候能够协调眼、手、脑的综合参与，通过圈画找出问题的关键点，或者通过画线段图、示意图把暗藏的数量关系清晰明朗，从而找到解决问题的突破口;二是让学生在审题的时候能够联动自己已有的知识体系，通过数学语言的相互转译达到通过表面透视到问题的本质，从而拨开一些外在的信息干扰直击问题核心;三是让学生在审题的时候不拘泥于单一的题目，能灵动地进行思维类比、联想和辐射，从而清晰地把握住与此相关或者相似题目的联系或区别，或者以此为点的知识结构的建构。

二、一般审题与动态审题的关联

一般审题的主要表征就是用眼睛看，靠想象来整理信息，往往只见树木不见森林，当单一、静态的审题方式遇到数量关系隐蔽或者信息稍复杂的时候就会束手无策。动态审题强调的是多感官的综合参与，强调通过画图、转译、联想等方式对信息进行梳理、透视和辐射，从而实现没有头绪中找到突破、繁难题目实现简易转化、窥一斑而知全豹的目的。

1. 一般审题重在动眼，动态审题基于动手

审题是一个对题目中的有用信息进行输入、处理，然后输出的复杂过程。但是因为一般题目的数量关系都清楚简单，学生用眼睛阅读后就可以直接把问题解决掉，所以很多学生养成了“看题目”的审题方式。但是随着知识的增多，题目的变化越来越复杂，“看题目”的方式只能让更多的学生无所适从，当面临稍微复杂的题目时经常出现不尝辄止、过早否定自己的消极态度。

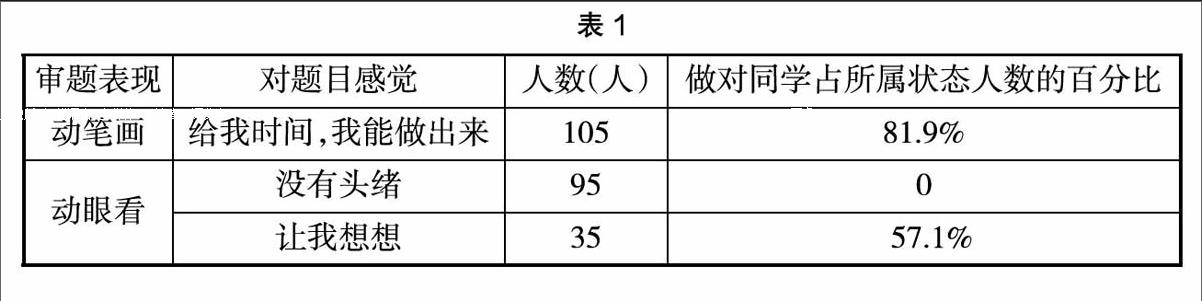
笔者带着一道略微复杂的题目对本校六年级（4个班，共235名学生）进行了两次调查（在学生刚刚学完圆柱体积计算之后）和一次访谈，情况如下：

第一次：“把一个正方体削成一个体积最大的圆柱，圆柱体积是正方体体积的几分之几？”（教师没有任何要求和提示）

在第一次没有动笔画图但是也做对的学生当中，当问及为什么不画图也能做对呢？他们回答说在脑子中画图的，这部分人属于抽象思维特别出色的，但是因为其抽象思维并不成熟，所以导致正确率并不高。

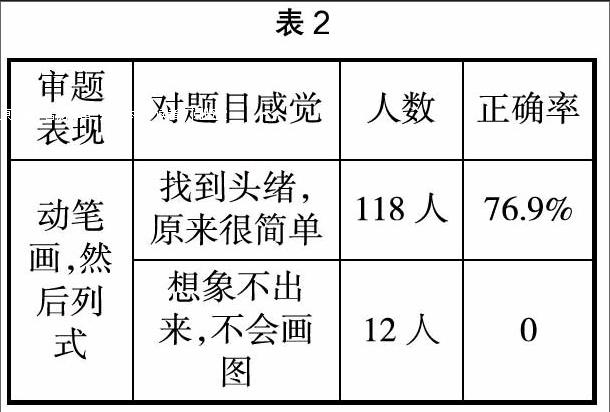
第二次：教师强制要求130人都动笔画图，然后再对答案，结果如下：

经过这样反复比较，教师进行了第三次调查。此次调查采取访谈形式。

师：一开始觉得题目难度怎么样？后来呢？

生：一开始觉得题目不好做，不知道该怎么下手。后来画图之后觉得原来挺简单的。

师：以后面对看起来不好处理的问题时，你想怎么应对？

生：画图。

2. 一般审题着眼形式，动态审题注重本质

在刚学了乘法分配律a×c+b×c=（a+b）×c之后，练习中出现了如99×78+78这样的题目大多数学生就迷糊了。他们不知道此形式与彼形式之间本质的联系：都表示两个数分别与同一个数相乘再相加，相当于把两个数先相加再同这个数相乘。一般的审题只看到形式，看不到形式背后的本质。数学书上的陈述一般都是一种严密的学术形态，只有少数优秀的学生能够跨过“抽象”的门槛，严格地按照形式化的叙述把握数学本质含义。但是对于大多数学生来说，我们需要学会把数学叙述转译成“非形式化”的语言去理解，或者把数学叙述转译成图象去探索，又或者转译成数学符号去把握等，这样才能帮助我们探寻到现象背后的本质，对解决问题有曲径通幽、直击核心的效果。比如本题如果转化成这样的叙述，问题就迎刃而解了——“99个78加上1个78就是100个78，所以99×78+78=100×78”。

3. 一般审题旨在就题论题，动态审题强化举一反三

数学知识之间都是互相关联的，比如学生们学会了加法运算律的那套方法可以迁移到乘法运算律中运用，学习了长方形的周长、面积计算后，发现它可以同样运用到平行四边形和梯形中，这种迁移运用给学生带来巨大的成功体验，能充分体会到数学学习的乐趣。做题更是一种迁移学习活动，是否能举一反三、推一及百是数学素养高低的重要体现。

一般人在练习“把一个正方体削成一个体积最大的圆柱，圆柱体积是正方体体积的几分之几？”时做完就完了。但是如果能展开联想：“把一个正方体削成一个体积最大的圆锥，圆锥的体积是正方体的几分之几？”或者“把一个长5厘米、宽4厘米、高3厘米的长方体削成一个体积最大的圆柱体，圆柱体的体积是多少？”通过这样一联想，就可以把长方体、正方体、圆柱体、圆锥体等物体的体积以及相互之间的关系做个梳理。推一及三的做题方式可以有效促进知识由点及面，思维由点及面。

三、动态审题的实践路径

数学题目客观上是静态的，动态审题就是通过主观上的动手和动脑让静态的文字变得简洁、丰富。动态审题以主动、联动与灵动的特点可以有效地帮助学生在圈画、转译和联想中找准突破口，抓住本质核心，举一反三，从而助推思维的简化、质化与活化。

（一）动笔圈画——简化思维

审题本身是一种隐性的思维过程，无法显现和量化。正因为如此，很多孩子把本该三步思考的过程懒惰地减缩为两步或一步，从而导致信息零散缺乏联系，无法顺利解决问题。无论是线段图还是实物图，其实都是用可以看得见的方式强制性地把数学信息进行梳理和显现的过程。在动笔圈画的过程中，一些隐蔽的信息也能明朗起来，思路逐渐清晰。

1. 线段图——化隐为显

“线段图”具有直观形象的特点，是学生进行抽象思维的“拐棍”。尤其对一些较复杂的问题，通过线段图把重要信息进行梳理，使学生清楚地从图上看到一些隐含的数量关系，从而获取新的信息和解题线索，找到突破口。

比如：甲、乙两人骑车分别从东、西两村同时出发相向而行，相遇时距中点2.4千米。已知甲的速度是乙的2倍，那么东、西两村相距多少千米？

（甲的速度是乙的2倍，同样时间内说明路程就是乙的2倍）

从图1中可以看出，甲的路程比中点多2.4千米，乙的路程比中点少2.4千米，所以甲比乙多2.4×2=4.8千米;又因为甲的路程是乙的路程的2倍，即比乙多1倍，所以 4.8千米就是一倍的路程，所以全程就是4.8×3=14.4千米，线段图立刻使隐含的数量关系明朗起来。

2.示意图——化抽象为形象

小学生心理正处于具体形象思维阶段，学生的数学学习更多地依赖于实物或图形等直观材料的支持。实物图或示意图可以将许多抽象的数学概念、算理、数量关系形象化、简单化，给人以直觉的启示。因此，巧妙合理地运用实物图或示意图这种简便易行的教学方式，有助于学生思路的开启。

比如“有一桶油，连油带桶一共重18千克，倒掉一半的油以后，连油带桶一共重10千克，油重多少千克？桶重多少千克？”

这种也属于非普通数量关系的题目，一般人找不到头绪。可是如果画出实物图一比较，就会豁然开朗。

面对这种图（如图2），通过一比较，自然就能发现问题：刚刚有18千克，现在怎么只有10千克了？说明少的8千克就是倒掉的一半的油，18-10=8千克，8×2=16千克。

（二）语言转译——质化思维

数学问题一般都是正规的严密叙述，对于小学生来说，其高度的简洁和抽象很容易让人感觉无从下手。但是如果能把静态的数学语言动态地转译为通俗易懂（自然语言）、浓缩概括（符号语言）、简洁直观（图形语言）等其他的表达方式，就能帮助学生很好地把握住问题的本质。

1. 类比化转译——去现象为本质

有些问题的情境离学生生活实际比较远，如果类比成熟悉简易的情境，立刻就能凸显出本质;有些问题是动态变化的，类比成静止的就更容易入手。

比如火车相遇问题：“快、慢两车分别长150米和200米，相向行驶在平直的轨道上，若快车的速度是30米/秒，慢车的速度是20米/秒，两车从相遇到相离需要几秒钟？”这道题最大的障碍是：火车本身有长度，而且两辆车都是动态的，这给问题的解决带来很大难度。

如果采用类比的策略，把两辆车类比成两个人的话，当两车头相遇时（如图3），车尾的两个人的位置就会如图3中的△，当两车车尾相离时，两个人会在中间重合（就是相遇）。这道题可以转译成“甲、乙两人从两地相向而行，两地相距150米加200米，甲速是30米/秒，乙速是20米/秒，两人要几秒钟相遇？”经过这样类比就变成了一般的相遇情境，问题迎刃而解。

2. 符号化转译——去繁难为简易

数学符号化，是数学形式化的基础。符号语言以其独有的精确、简约、便于推理和运算，对数学问题的解决有重大作用。在解决问题的过程中，如果能灵活地把数学语言转译成符号语言，对解决问题有化繁为简的突出效果。

比如“一个素数的3倍和另一个素数的2倍之和是100，这两个素数的乘积是多少？”从数学语言文字的表面找不到什么突破，如果把这道题转译成字母式就会豁然开朗了。假设第一个素数为a，第二个素数为b，可以列式为3a+2b=100，因为100是偶数，2b肯定也是偶数，所以3a也是偶数，3跟一个素数的乘积是偶数，这个偶数只能是2了，第一个素数是2，后面一切都水到渠成。

四、结语

在审题时，我们不仅需要读懂题目中的文字叙述，更要理解叙述中所反映的实际背景，领悟从背景中概括出来的数学实质。动态审题是读懂、理解和领悟的利器，不仅是一种习惯，更是一种学习能力，需要教师们持之以恒地培养和训练。