一种改进的基于分水岭的图像分割算法
凌财进,曾 婷,张 超,黑霞丽
(1.河源职业技术学院 电子信息工程学院,广东 河源 517000 2.美国特拉华州立大学 工程学院,美国 特拉华 19904)
一种改进的基于分水岭的图像分割算法
凌财进1,2,曾 婷1,张 超2,黑霞丽2
(1.河源职业技术学院 电子信息工程学院,广东 河源 517000 2.美国特拉华州立大学 工程学院,美国 特拉华 19904)
针对分水岭算法过分割现象,提出一种综合分水岭算法、中值过滤算法和归一化割算法的改进算法;该算法首先应用改进型的中值过滤算法对图像进行适当的除噪;然后通过分水岭变换对图像进行了初步分割,最后使用归一化割算法进行图像精度分割;算法集合了分水岭算法、中值过滤算法及归一化割算法的优点,既较好地解决了分水岭算法中过度分割的问题,又降低了归一化割算法的时间复杂度;实验结果表明该算法是一种切实可行的图像分割方法。
图像分割;分水岭;归一化割;中值过滤
0 引言
图像分割是图像分析与模式识别中的一个重要问题,分割目的就是将图像根据一定的规则划分为若干个有意义的区域,从而实现图像高层次的分析和理解。图像分割的质量是图像处理中的一个经典难题,多年来众多学者进行了广泛和深入的研究。
分水岭(watershed)法是一种基于数学形态学发展起来的一种图像分割方法。分水岭算法对微弱边缘具有良好的响应,能得到封闭连续边缘和较低的时间复杂度。传统的分水岭算法因对噪声敏感而产生过分割现象,使得感兴趣目标淹没其中。业界认为传统的分水岭算法不能单独应用于实践。因此,本文提出一种融合中值过滤、分水岭变换和归一化割算法优点的图像分割方法,即3IN1-Cuts算法。
1 相关研究
上述我们提到传统分水岭算法存在着过分割缺点,因此不能单独应用于实践,于是学者们进行了实践与研究,提出了各种改进型分水岭算法,不少已成功应用于实践和生产中。 文献[1]中Nguyen 和Worring等人提出能量驱动的Water snakes算法,新算法对边界定位准确度和连续性有较好的改进,但无法解决过分割问题;文献[2]中来自加拿大的Demin Wang提出了应用梯度公式对图像进行预处理以消除噪音,效果并不理想;文献[3]崔明等人通过阈值标志法,提出一种基于区域融合的改进型多尺度的快速分水岭变换算法,并将改进分水岭变换中获得的多尺度信息作为评价边界强度的指标,该算法还是属于阈值法与分水岭结合的范畴,由阈值决定了局限性;文献[4]中Haris 等人提出通过区域合并来缓解过分割,但分水岭变换产生大量区域,后续合并过程运算量极大,影响了算法的效率;针对文献[4],也有学者提出采用对输入图像的梯度取阈值的方法来降低过分割,事实证明采用阈值的方法虽然能解决过分割问题,但同时也使得图像中的部分细节;文献[5-6]提出采用分水岭变换和图论结合的分割方法,较好地解决了过分割问题;文献[7]陈忠和赵忠明通过一种叫PGF非线性滤波和快速多尺度合并算法有选择地对分水岭变换结果进行合并,实验结果表明该算法能获得良好的分割效果,但没从根本上解决过分割,还是分割后的合并。
从文献和实践中我们推断,要从根本上解决传统分水岭过分割问题,或许应尽量减少分割而不是分割后再大量合并。因此,我们认为从根本上解决过分割,主要解决3个问题:1)在不影响分割效果的前提下,分割前尽量减少或抑制噪声和细密纹理的影响;2)合理降低区域数量,降低运算;3)提高算法适用的鲁棒性,避免区域合并或减小合并难度和复杂度。 因此,针对问题我们提出了一种结合中值过滤、分水岭变换和归一化割的长处的图像分割方法(3IN1-Cuts),最后分类器根据提取的图像特征进行相应的分类,从而达到识别效果[4-5]。
2 相关理论和推导
在图像分割的算法中,中值过滤处理方法、分水岭分割法和归一化割法是目前常用的工具,并且它们各自有自己的优点和缺陷,下面简单介绍相关理论和其推导过程。
2.1 中值滤波
中值滤波由Turky在1971年提出,最初用于时间序列分析,后来被用于图像处理,并在去噪复原中取得了较好的效果。中值滤波器基本原理是把图像或序列中心点位置的值用该域的中值替代,具有运算简单、速度快、除噪效果好等优点[9]。通过二维滑动模板值滤波输出为:
g(x,y)=med{f(x-k,y-l),k∈w,l∈w}
其中:f(x,y),g(x,y)分别表示原始图像和处理后图像。传统的中值滤波算法计算效率低,要真正在实践中应用,需对其进行改进,提高效果和速度。文章第四部分提出使用改进算法进行快速除噪。
2.2 分水岭算法
分水岭分割算法是一种基于拓扑理论的数学形态学的分割方法,算法的设计思路是把图像的像素灰度值与地表海拔高度对应起来,因此“海拔”高度范围是[0,255];每一个区域局部极小值及其影响区域称为集水盆,而集水盆的边界则形成分水岭[8-10]。分水岭比较经典的实现方法有模拟降水过程和涨水过程,不同的方法实现思路和效果各有差别。其中,一个经典计算方法是Vincent L和Pierre S提出[11]的,在该算法属于涨水过程模拟类型,此计算方法分两个步骤,分别是排序过程和淹没过程。该算法中主要借用了分水岭算法的物体轮廓线的封闭性和精确性,对图像进行初步分割,得到封闭且精确的集水盆图像,并作为归一化割流程的输入。
2.3 归一化割算法
归一化割(Normalized Cut )法是1997 年由J.Shi 与J.Malik 提出的无人监督图像分割技术, 用于解决图像分割与聚类中的问题[5]。算法基本思路是将图像映射为无向带权图G,图的节点V由像素构成,图的边权值即为像素之间的相似度,利用最优割集准则对图进行划分,从而得到图像的最优划分[5]。对于一幅输入的原始图像或一个特征点集F建立一个带权的无向图G和节点V,关系E,则有G=(V,E)。假设图G可以通过删去某些边,将其分为两个非连接性的点集A,B,即产生两个新的子图,由图论定义可知:A∪B=V,A∩B=φ,这两个点集之间的不相似程度可以定义为原先连接G图的两部分而现在被删去的所有边的总和,图的分割过程如图1所示,

图1 归一化割算法示意图
结合图论中的“割”的定义,以上描述可以用数学表达为:

字母i和j分别表示两点,w(i,j)表示连接点i和点j的边的权值,也是两点间的相似度。 由割的定义公式可知,割与对应的割边的数目成比例,所以可以推导出新的不同组之间的不相似度量,即归一化割:
(3)
其中:assoc(A,V),assoc(B,V)分别表示A和B中的点与图中所有点之间总的联系程度。根据同一组内的相似性可推导组内相似性函数Nassoc:
(4)
Assoc(A,A)表示A中所有边的权和总和,Assoc(B,B)同理。由公式(3)、(4)得:
NCut(A,B)=2-Nassoc(A,B)
(5)
从公式(5)可知,在图的划分算法中,不同分组之间总体最小不相似性(NCut)与同一个组内部总体最大相似性(Nassoc)存在线性关系。因此,通过图像分割问题转换为图的划分问题,通过以上操作从而可以完成对图像的分割。
3 本文算法
3.1 3IN1-Cuts算法概述
3IN1-Cuts算法即中值过滤算法、分水岭算法和归一化割算法三者优点相结合的一个分割算法。这是为解决分水岭算法的过分割问题,提出一种综合的改进算法。算法第一步是利用中值滤波方法对图像进行去噪,并保持照片细节和边缘,以减少噪声对图像初次分割结果的影响;第二步利用了分水岭算法对微弱边缘具有良好的响应并保证其连续封闭,能为图像分析提供封闭的集水盆的优点,对去噪后的图像进行分水岭变换,得到输入图像的集水盆,实现图像的初步分割;最后,根据初步分割得到的结果建立简化的无向网络图G
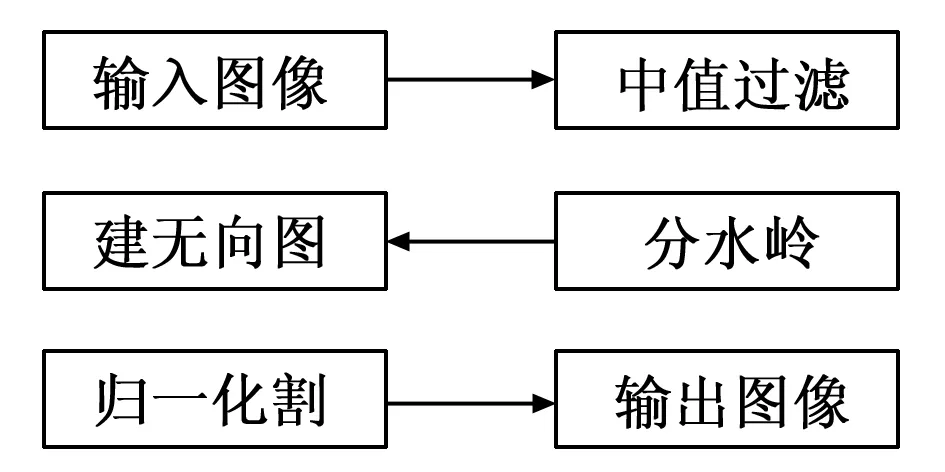
图2 算法主要框架
3.2 采用中值过滤进行预处理
1)分割前的准备工作,包括彩色图像转换工作和噪声消除工作。灰度图像计算分析不仅计算速度快,而且计算误差少,因此本文把彩色图像转为灰度图像进行分析和计算。一般彩色与灰度转换由公式(6)实现,为避免公式(6)三次的浮点数运算消耗时间大,因此先放大倍数再通过移位来缩小相应倍数,即公式(7):
Gray=0299R+0.587G+0.114B
(6)
Gray=(77R+151G+28B)shr8
(7)
2)除噪运算。考虑传统的中值过滤排序耗时多,本文采取了高速排序的方法,对一个区域内的像素排序同步进行,从而进行快速过滤。在不破坏区域重要轮廓与图像细节的的前提下采用改进后的中值滤波算法来消除部分噪声,并对原始图像的梯度图进行开闭重建运算,去除了噪声。其中,中值滤波运算中权系数矩阵模板W为:
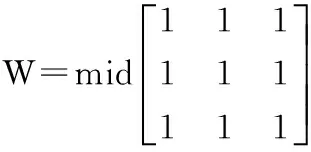
(8)
3.3 利用分水岭变换进行初步分割
分水岭第一步是求解每个相素对应的梯度值,设f(x,y)表示经过灰度变换和中值过滤后图像的像素,由像素计算梯度值grad(x,y),计算方法如下:


令M1,M2,…,Mi为图像grad(x,y)的局部最小值点的坐标的集合,令G(Mi)为位于与局部最小值点坐标的集合,相应区域的Mi点的集合在相联系的汇水盆地内。假设min和max分别代表g(x,y)的最小值和最大值,同时令T[n]为坐标(s,t)的集合,其中g(s,t) (10) (11) 在几何上,T[n]是g(x,y)中的点的坐标集合,集合中的点均位于平面g(x,y)=n的下方,计算是个不断迭代的过程,经过比较与排队从而完成梯度图像的排序。 通过分水岭变换得到的是经过中值过滤图像的集水盆;接着,根据集水盆与集水盆之间的关系得到各区域的分水岭,即相应区域内的图像极大值点;此外,为得到图像的边缘信息,需构造梯度值并把梯度图像作为计算的输入;最后,迭代计算得到较好的图像边界信息,为实验第三步即归一化割进行精细分割提供了可能。 3.4 采用归一化割精细分割 di表示点i与其他点之间的联系程度,因此,NCut 可以重写成如下 设D=diag(d1,d2,…,dN),W是N×N的对称矩阵, 且W(i,j)=wij。 这样寻找全局最优值简化为: (13) 假设y为实值,则公式可以通过广义特征值问题对公式(13)求解: (14) 由指示向量x的决定了变量y。公式(14)可以写成规范特征值问题: (15) 该特征值问题的对应具有第二个最小特征值。同理可求得第三小特征值向量,然后采用递归逐个求解,从而完成图像的分割。 3.5 本文算法实现步骤 本文算法实现主要过程包括12个步骤,如表1所示。 表1 3IN1-Cuts算法实现步骤 本实验环境为W541型移动工作站,处理器为IntelCorei7-4810MQ,内存是16G,固态硬盘256G,软件环境VisualC++ 2015,为了验证上述算法的有效性, 实验对取自美国加州大学伯克利分校电子图像分割图库中的标准图像50 幅进行了测试。其中,图3中的图像规格都是481×321,其中(a)为图库编号119082的原始图像, (b)、(c)和(d)分别是传统分水岭、归一化割算法及本文算法(3IN1-Cuts)的分割结果。从图3四幅图像的实验结果,可以明显得到本文算法(3IN1-Cuts)的分割效果比传统分水岭和归一化割的结果要好得多。 图3 本文算法与传统算法实验比较 此外,我们还与分水岭的部分文献中提到的改进算法进行了比较,图4中的图像规格是481×321,(a)为图库编号42049的原始图像,图(b)、(c)和(d)分别是文献[3]、文献[5]和本文算法的分割结果。显然,文献[3]算法因阈值导致图片细节丢失,从图4四幅图像的实验结果,可以明显得到本文算法(3IN1-Cuts)的分割效果比文献[3]和文献[5]的分割结果要好。 图4 本文算法与文献算法实验比较 此外,我们还对相应的分割时间进行了对比,以编号为119082的图像为例,具体如表2所示。 显然,除了无实用价值的传统分水岭算法外,3IN1-Cuts算法在分割相同的图像时消耗时间是最小的(图像效果也是最好的,见图3与图4),分别比文献[3]和文献[5]的改进算法低1.13和0.12秒。从实验结果可推断,利用改进后的中值过滤算法适度除噪,利用分水岭变换的优点进行初步分割及归一化割的稳定性,能较好地整合了三者的优点,不仅取得较好的分割效果,还在时间复杂度方面得到优化。 表2 五算法耗时统计表 本文针对传统分水岭算法过分割现象,提出一种基于分水岭、中值过滤和归一化割算法的综合优化算法,该算法综合3种算法的优势,较好地解决分水岭过分割问题,提高了分水岭算法的分割精度,并且降低了归一化割算法的时间复杂度。文章最后通过实验对比证明本文算法与同类改进算法相比在分割效果和时间消耗方面取得了较好的效果。 [1]NguyenHT,WorringM,BoomgaardRVD.Watersnakes:energy-drivenwatershedsegmentation[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2003, 25(3):330-342. [2]WangD.Amultiscalegradientalgorithmforimagesegmentationusingwatersheds[J].PatternRecognition, 1997, 30(12): 2043-2052. [3] 崔 明, 孙守迁, 潘云鹤. 基于改进快速分水岭变换的图像区域融合[J]. 计算机辅助设计与图形学学报, 2005,17(03):546-552. [4]HarisK,EfstratiadisSN.Hybridimagesegmentationusingwatershedsandfastregionmerging[J].IEEETransactionsonImageProcessing, 1998, 7(12): 1684-1698 [5] 杨卫莉, 郭 雷. 基于分水岭算法和图论的图像分割[J]. 计算机工程与应用, 2007, 43(7):28-30. [6] 冯 林, 孙 焘, 吴振宇, 等. 基于分水岭变换和图论的图像分割方法[J]. 仪器仪表学报, 2008,29(3):649-653. [7] 陈 忠, 赵忠明. 基于分水岭变换的多尺度遥感图像分割算法[J]. 计算机工程, 2006,12(23):186-187. [8] 李海滨, 杜益福, 刘 彬. 基于图割和分水岭变换的图像分割方法[J]. 燕山大学学报, 2013, 37(2):143-147. [9] 黄思博. 基于计算机视觉的异常驾驶行为检测方法研究[D]. 广州:华南理工大学,2011. [10] 高 欣. 基于彩色超声图像的血管内膜中层厚度测量算法的研究[D].哈尔滨:哈尔滨工业大学, 2010. [11]VincentL,PierreS.Watershedsindigitalspaces:Anefficientalgorithmbasedonimmersionsimulations[J].IEEETrans.onPatternAnalysisandMachineIntelligence, 1991, 13(6):583-598. An Image Segmentation Based on Improved Watershed Ling Caijin1,2, Zeng Ting1, Zhang Chao2, Hei Xiali2 (1.College of Electronic Information Engineering, Heyuan Polytechnic, Heyuan 517000, China;2.College of Engineering, Delaware State University, Dover 19904, USA) In order to overcome the shortcoming in over-segmentation of traditional watershed algorithm, this paper presented an improved image segmentation method, which is having performance advantage of watershed, median filter and normalized cuts. Firstly, an improved median filter is applied to reduce the image noise. Secondly, watershed transform is used to pre-segmentation. Finally, normalized cuts is employed to deal with detail segmentation. Segmentation experiments show that this method which contains good performance of the three steps, can not only effectively avoid the over-segmentation of watershed, but also reduce the time complexity of normalized cuts. image segmentation; watershed; normalized cut; median filter 2015-08-27; 2015-09-25。 广东省教育科学“十二五”规划教育信息课题(13JXN035),广东省教育教学改革项目(201401232),广东省高职高专校长联席会议课题(GDXLHYB037) 。 凌财进(1983-),男,广东河源人,硕士,讲师,主要从事虚拟现实、图像处理与识别、物联网安全、计算机视觉等方向的研究。 黑霞丽(1981-),女,博导,主要从事计算机视觉、物联网安全方向的研究。 1671-4598(2016)06-0214-04 10.16526/j.cnki.11-4762/tp.2016.06.059 TP391.41 A

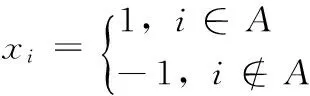
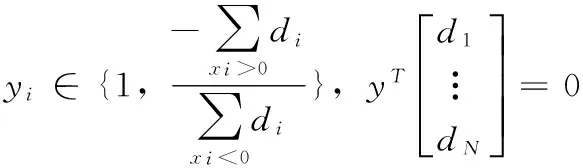


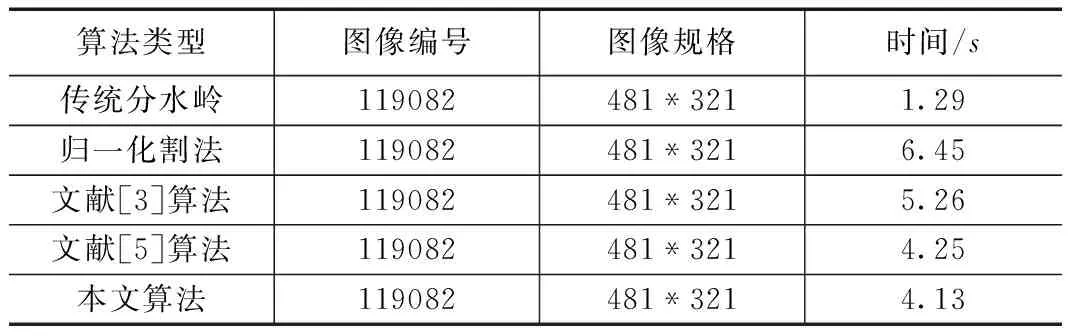
4 实验结果与性能分析


5 结论

