精密离心机主轴回转误差测量仿真技术研究
张 荣,牛宝良,凌明祥,王 珏, 周继昆
(中国工程物理研究院 总体工程研究所,四川 绵阳 621900)
精密离心机主轴回转误差测量仿真技术研究
张 荣,牛宝良,凌明祥,王 珏, 周继昆
(中国工程物理研究院 总体工程研究所,四川 绵阳 621900)
精密离心机主轴回转误差直接影响精密离心机动态半径的测量、离心加速度输出精度以及精密离心机主轴运行安全性,必须精确测量主轴回转误差参数;介绍一种应用3个电容测微仪测试并分离主轴回转误差与圆度误差的方法,利用MATLAB对三只电容测微仪安装角度误差、主轴全周采样点数、测试系统本底噪声对主轴回转误差测试结果影响进行仿真分析,得出采样点数N、测微仪安装角度误差δα、δβ以及测试系统本底噪声对回转误差分离的影响,基于仿真结果确定了10-6量级精密离心机主轴回转误差测量的几个工程参数。该方法已应用于某高精度精密离心机主轴回转误差精密测试中,实测表明,转速在300 rpm内精密离心机纯回转误差测量结果为0.25 μm,满足10-6量级高精度精密离心机的研制指标需求。
精密离心机;回转误差;圆度误差;三点法;电容测微仪
0 引言
精密离心机空气主轴径向回转误差是影响高精度精密离心机性能的重要因素,主要表现在:1)在利用外基准测量精密离心机动态半径时,主轴径向回转误差将混入动态半径测量值中,回转误差量级较大时,其对动态半径的影响不可忽略,必须对动态半径进行补偿,否则经离心加速度补偿模型[1]输出的加速度信号精度无法得到保证;2)主轴径向回转误差直接关系到主轴运行安全,对于空气静浮主轴,气膜厚度通常仅几微米,为保证离心机在各G值下安全运行,必须对主轴的回转运动误差进行监视,设定主轴回转运动误差限,当主轴回转运动误差接近超限值时,离心机必须停机。因此,为满足高精度精密离心机研制技术指标,对其主轴的回转运动参数必须进行精确测量。针对某10-6量级精密离心机研制,精密离心机主轴回转误差的精度指标为≤0.5 μm,为完成该参数的高精度测试,笔者提出采用电容测微仪和三点法进行测试,并设计精密测试系统完成了10-6量级精密离心机主轴回转误差的测试,实测主轴纯回转误差为0.25 μm。
1 精密离心机主轴回转误差测试方法研究
目前,对于10-5及以下量级精密离心机研制,由于量级低,主轴回转误差的量值大小对精密离心机输出加速度精度影响不明显,而主轴运行安全性监测是主要的,常采用在主轴截面上安装两只[2-3]正交的电容传感器测量主轴转动一周测微仪输出最大值与最小值,这种测量无法测试出纯主轴回转误差运动极值。对于10-6及以上量级的精密离心机研制,必须考虑主轴安全性以及主轴运动误差对动态半径的贡献,采用双测微仪法测试无法满足测试要求,必须采用新的测试手段。
1.1 主轴回转误差测试的难点
主轴回转误差测试难点在于通常主轴圆度误差和回转误差同时混杂于测试结果中,并且圆度误差往往比回转误差大得多,测试纯回转误差较难,解决方法有两种:一种是借助于安装在主轴上的标准球,采用电容非接触式或电感接触式测试标准球的径向跳动量,此时忽略标准球圆度误差,采用正交双测微仪合成李萨如[4]图获得主轴回转误差,但该法仅适用便于安装标准球的场合,同时标准球的安装还存在偏心误差,必须在测量结果中进行一次谐波分离去偏心误差;对不便安装标准球的测试,如本项目中的精密离心机主轴,采用在主轴外沿安装测微仪测试,测试结果包括了主轴回转误差和圆度误差两类信号,必须通过测试方法从结果中分离出圆度误差信号,得到真实的回转误差信号,故信号分离算法是关键。目前基本的圆度误差分离方法有反向法[5]、多点法[6]、多步法[7]等,多点法分两点法、三点法、四点法等。表1[8]是几类误差分离方法精度统计,通常各方法应用在不同的测试场合,但对于回转误差的总体分离精度均可控制在10%以内,这为本项目中空气主轴的回转误差的测试奠定了基础。从技术实现难易程度、成本等综合考虑选择在项目中应用三点法测试主轴回转误差。

表1 回转误差与圆度误差分离方法及误差表
1.2 三点法主轴回转误差分离测试原理
在主轴截面圆周布置3个电容测微仪S1、S2和S3,假设各测微仪中心交于同一点,且该点为空气主轴平均回转中心。电容测微仪S2、S3与S1的夹角分别为α和β,三电容测微仪采集数据为S1(θ)、S2(θ)和S3(θ),其中每个数据是空气主轴圆度误差、表面粗糙度以及径向回转误差的混合值。如图1所示,当主轴顺时针方向旋转时,3个测微仪的输出信号可表示为式(1):
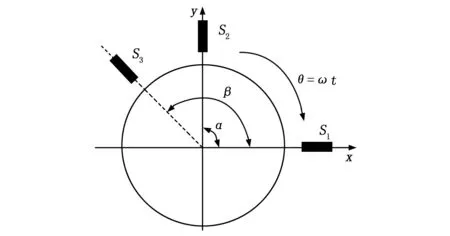
图1 三点法主轴回转误差分离测试示意图
(1)
式中,r(θ)为空气轴承形状误差的极坐标形式,以逆时针方向为正;x(θ)为径向回转误差在x轴方向的分量;y(θ)为径向回转误差在y轴方向的分量。
引入测微仪标定系数c1、c2,将S1(θ)、S2(θ)和S3(θ)测微仪测量值进行加权线性组合,有:
(2)
将式(1)代入式(2)并令x(θ)、y(θ)项的系数为零,可将主轴径向回转误差从测微仪输出数据的线性组合中去除,即得式(3):
(3)
解式(3)得式(4):
(4)
当测微仪的标定系数c1、c2满足式(4)时,3个电容测微仪的线性组合数据只含圆度误差,从而实现了圆度误差与径向回转误差分离,得式(5):
(5)
由于主轴形状误差具有径向性和周期性两个特征。径向性是指形状误差的量值反映在圆周的半径方向上;周期性是指形状误差的变化具有周期性,周期为2π。对r(θ)作傅里叶变换,得式(6):
(6)
式(6)中不存在零阶直流分量,因为电容测微仪输出数据减去初始间距值即为位移变化量。将式(6)代入式(5),得式(7):
(7)
其中:
(8)
对S(θ)作傅氏变换得式(9):
(9)
比较式(9)和式(7)得式(10):
(10)
解该方程组可得式(11):
(11)
主轴旋转一周测微仪等间隔采集N点并设:
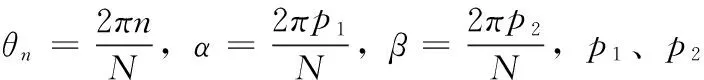
(12)
其中各系数表达如式(13)所示。
由式(13)可知,采样点数N、测微仪安装角度误差以及谐波分析阶次均会给分离精度带来影响,故须根据谐波分析阶次与分离精度要求确定三测微仪安装角度;根据ISO标准,当被测零件圆度误差的谐波次数大于22~45阶后,可将其归结为零件表面粗糙度和波度[9],本项目参考ISO标准,设定主轴圆度误差谐波上限为45阶,45阶以上的谐波成分将作为表面粗糙度与波纹度处理。圆度误差分离完成后,则回转误差也即得到分离。
2 主轴回转误差分离测试影响因素的仿真分析
精密离心机主轴回转误差测试实际设计时,需确定主轴全周采样点数N、三测微仪安装角度误差以及测试系统本底噪声对回转误差分离结果的影响程度,为此在MATLAB下进行仿真分析,以确定采样点数N和测微仪的安装角度α、β。
(13)
将式(13)代入式(1),可得主轴径向回转误差分量如式(14)所示:
(14)
仿真方法:假定主轴圆度误差和径向回转误差曲线,将两类信号叠加后利用三点法分离算法验证回转误差与圆度误差分离效果。设在主轴截面上每周采样N点数据,设假定的圆度误差r(θ)与回转误差e(θ)均用μm表示,r(θ)信号的幅值、相位可任意改变,r(θ)的各阶谐波的幅值和初相位角均由随机函数表示:
angle(r(θ))=rand(1,N)×pi;
r(θ)的谐波频率成分由角度θ和谐波次数k控制,最高谐波次数为Km,则r(θ)可表达为:
利用软件生成圆度误差r(θ):
rfz=rand(1,N)*1e-6; %r(θ)的幅值设定;
rxw=rand(1,N)*pi; %r(θ)的相位设定;
dth=(0:N-1)/N*2*pi;%θ角度离散化值;
for k=1:Km%r(θ)信号频率合成;
r=r+rfz(k)*sin(dth*k+rxw(k));
end
对于回转误差e(θ),设为四阶谐波的组合表达,四阶谐波的幅值与相位可任意设定,并加入测试系统噪声。此处也可将e(θ)的幅值、频率、相位均设计为随机数,其仿真结果不会因参数改变得出截然相反结论。利用软件生成四阶回转误差e(θ)的虚拟信号程序如下:
e01=9.40e-6*1;%e(θ)第一阶谐波幅值;
e02=6.30e-6*1;%e(θ)第二阶谐波幅值;
e03=2.20e-6*1;%e(θ)第三阶谐波幅值;
e04=1.10e-6*1;%e(θ)第四阶谐波幅值;
e01xw=10*pi/180;%e(θ)第一阶谐波相位;
e02xw=50*pi/180;%e(θ)第二阶谐波相位;
e03xw=30*pi/180;%e(θ)第三阶谐波相位;
e04xw=40*pi/180;%e(θ)第四阶谐波相位;
zsfz=1e-6;%e(θ)中引入的随机噪声幅值;
e=e01*sin(dth+e01xw)+e02*sin(dth*2+e02xw)+e03*sin(dth*3+e03xw)+e04*sin(dth*4+e04xw)+zsfz*rand(1,nmax);
设三只电容测微仪安装角度分别为P0、P1、P2;其中令P0=0°,P2、P3人为设定,考虑到在传统的两点法主轴回转误差测试方案中,主轴同截面上的两只电容测微仪是垂直布置的,为兼容传统的双截面两点法测试主轴回转误差方案,仿真时设P2为90°,P3设为157°,设对主轴全周采集N点,主轴圆度误差的信号成分k从1阶到45阶取值。
2.1 采样点数N对回转误差测试影响仿真
分别设定N=128,N=512进行仿真,回转误差与圆度误差的分离结果如图2~图5所示。
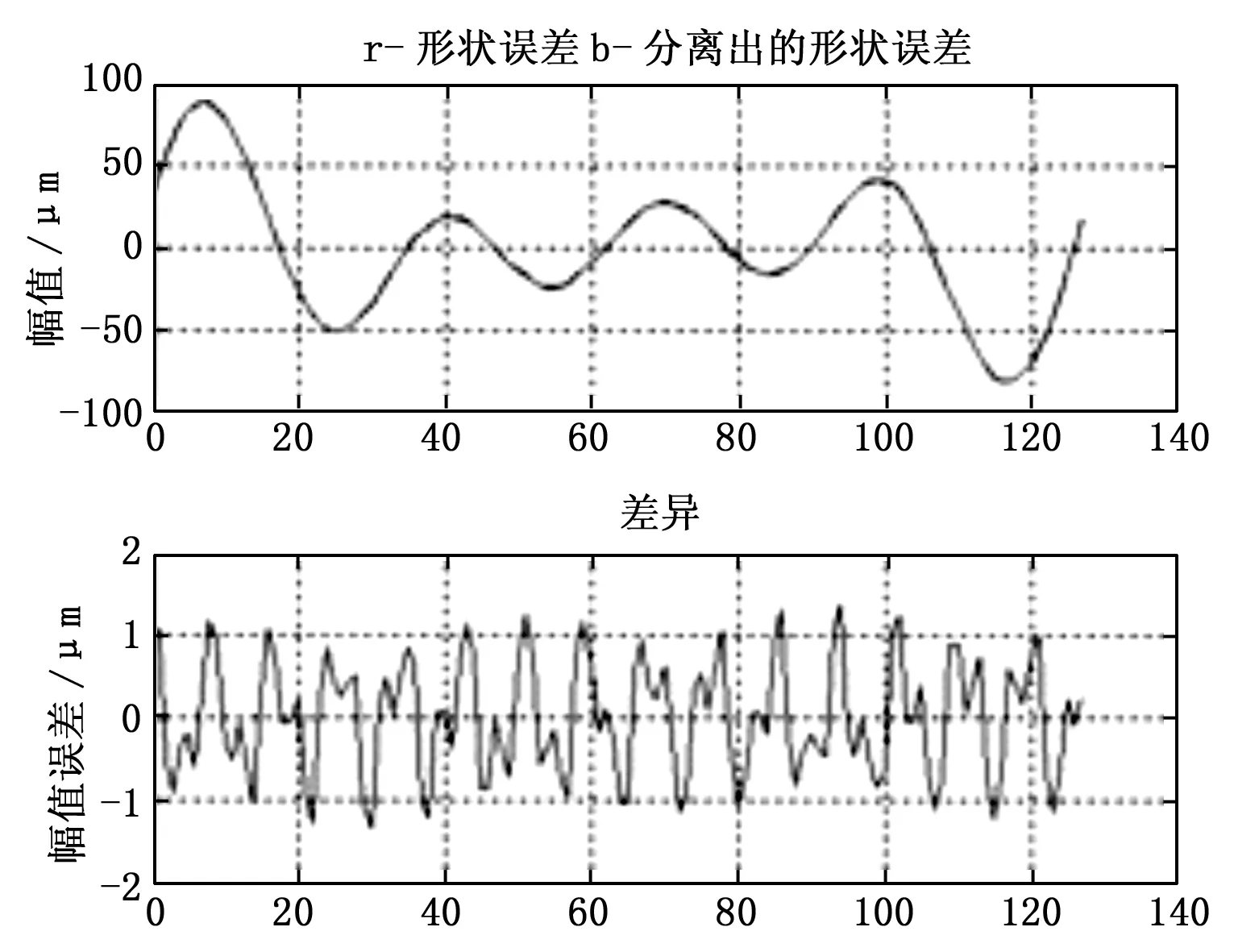
图2 N=128时圆度误差设定与分离结果
从仿真结果看,N值越大,回转误差与圆度误差的分离精度越高,适当选择N值可使圆度误差分离信号的误差达10-13量级。本项目中N取1 600点。
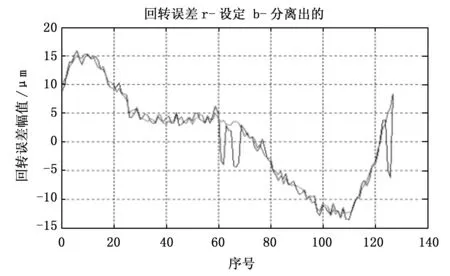
图3 N=128时回转误差设定与分离结果
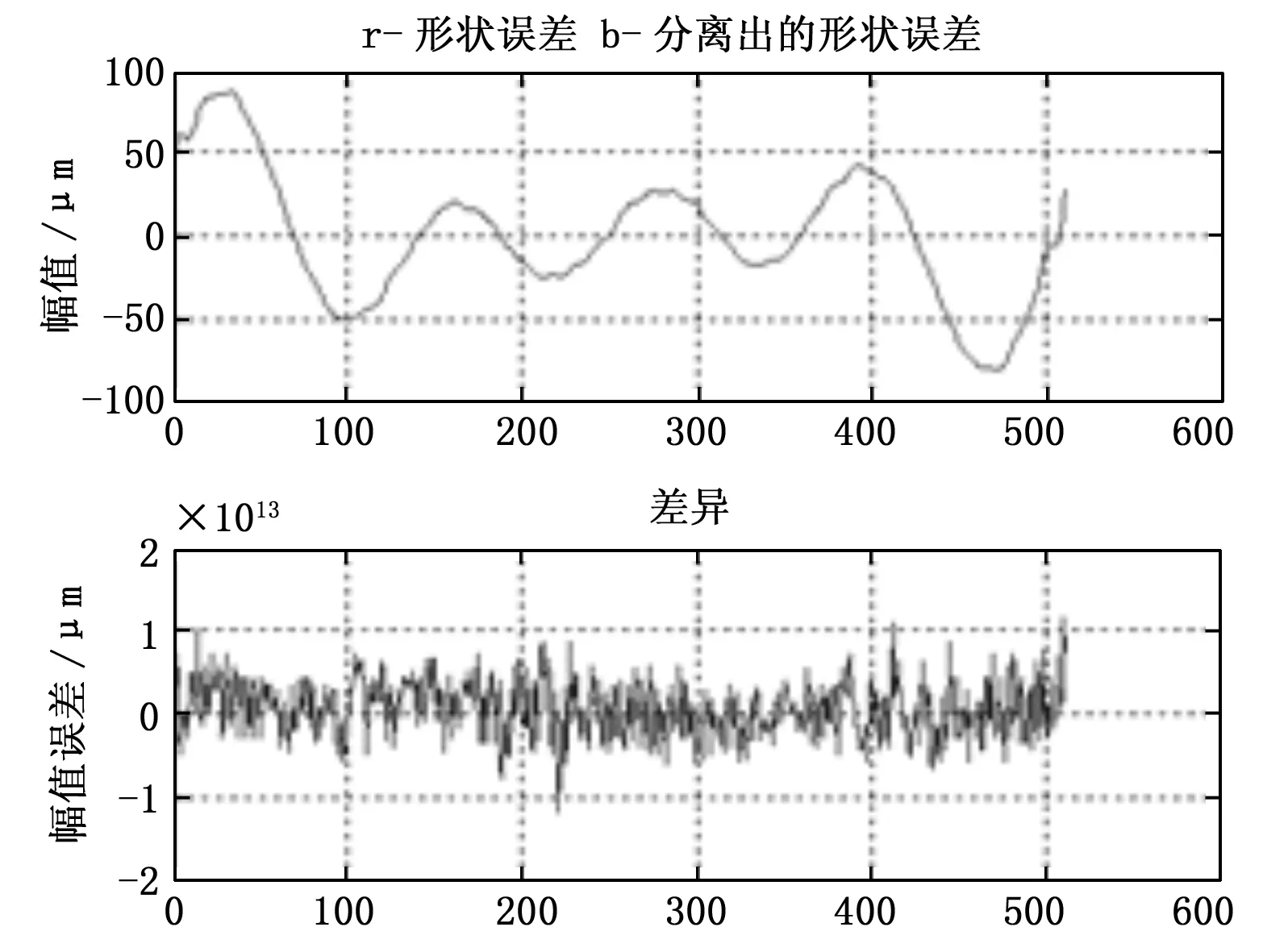
图4 N=512时圆度误差设定与分离结果
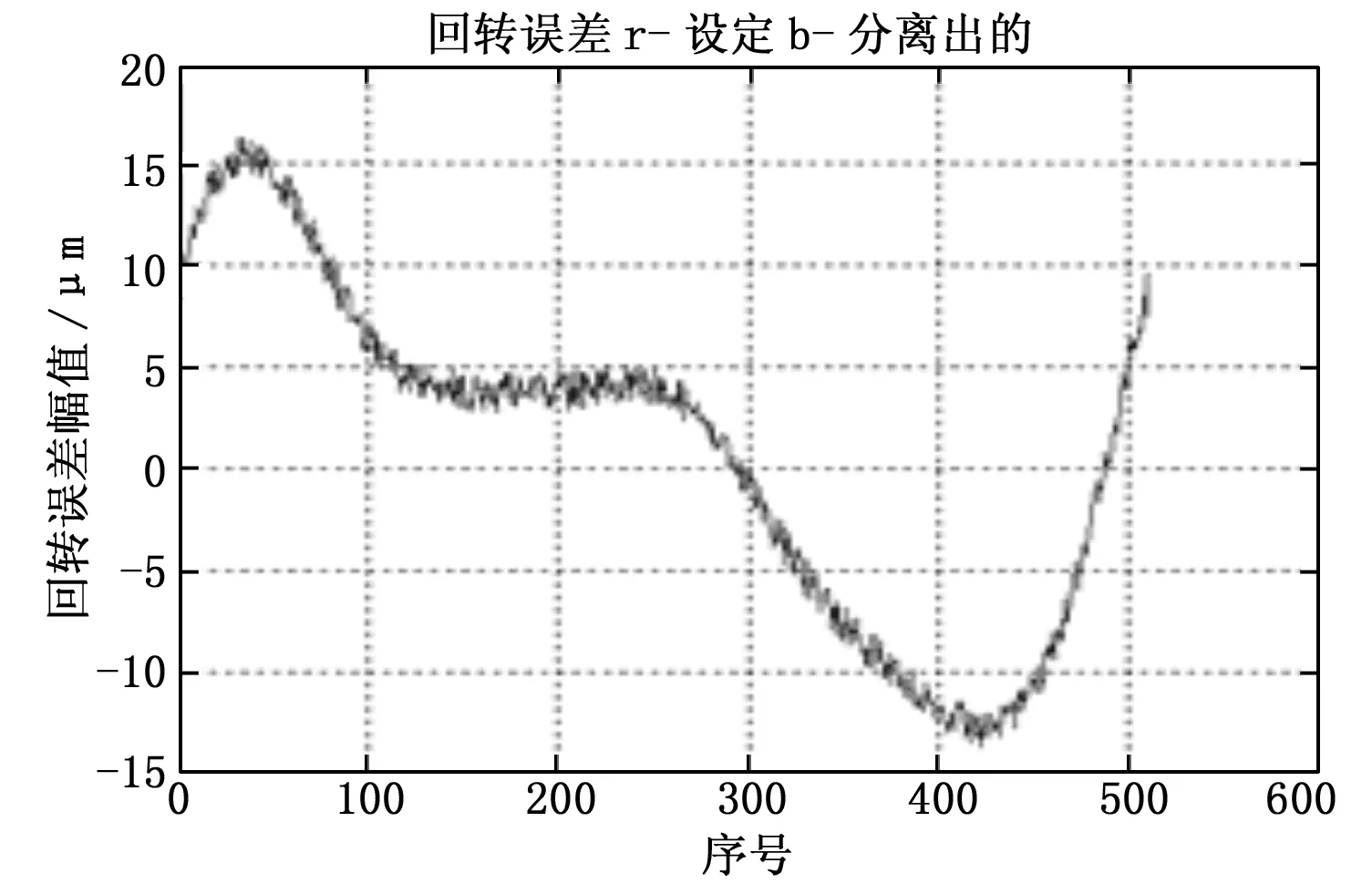
图5 N=512时回转误差设定与分离结果
2.2 测微仪安装角度对回转误差测试影响仿真
设三只测微仪理论安装角度分别为0°,α=90°,β=157°。工程设计时因测微仪装配误差使各安装角度存在误差,以第一只测微仪安装位置为参考,第二只与第三只测微仪相对于第一只测微仪的安装夹角存在偏差δα、δβ,仿真δα、δβ对回转误差分离结果的影响。考虑到离心机最高转速为300 rpm的工程实际,设测微仪安装偏差角δα、δβ控制在±1°范围内,在输入信号和采样点数N=1 024不变时,开展如表2仿真分析,给出代表性的仿真结果如图6~图9所示。
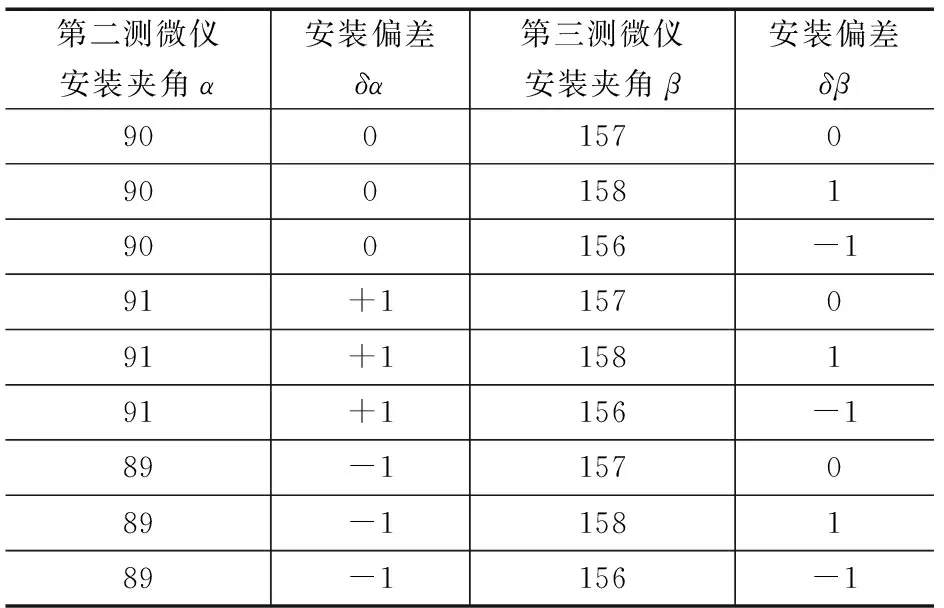
表2 仿真测试测微仪安装角度偏差δα、δβ表 (°)
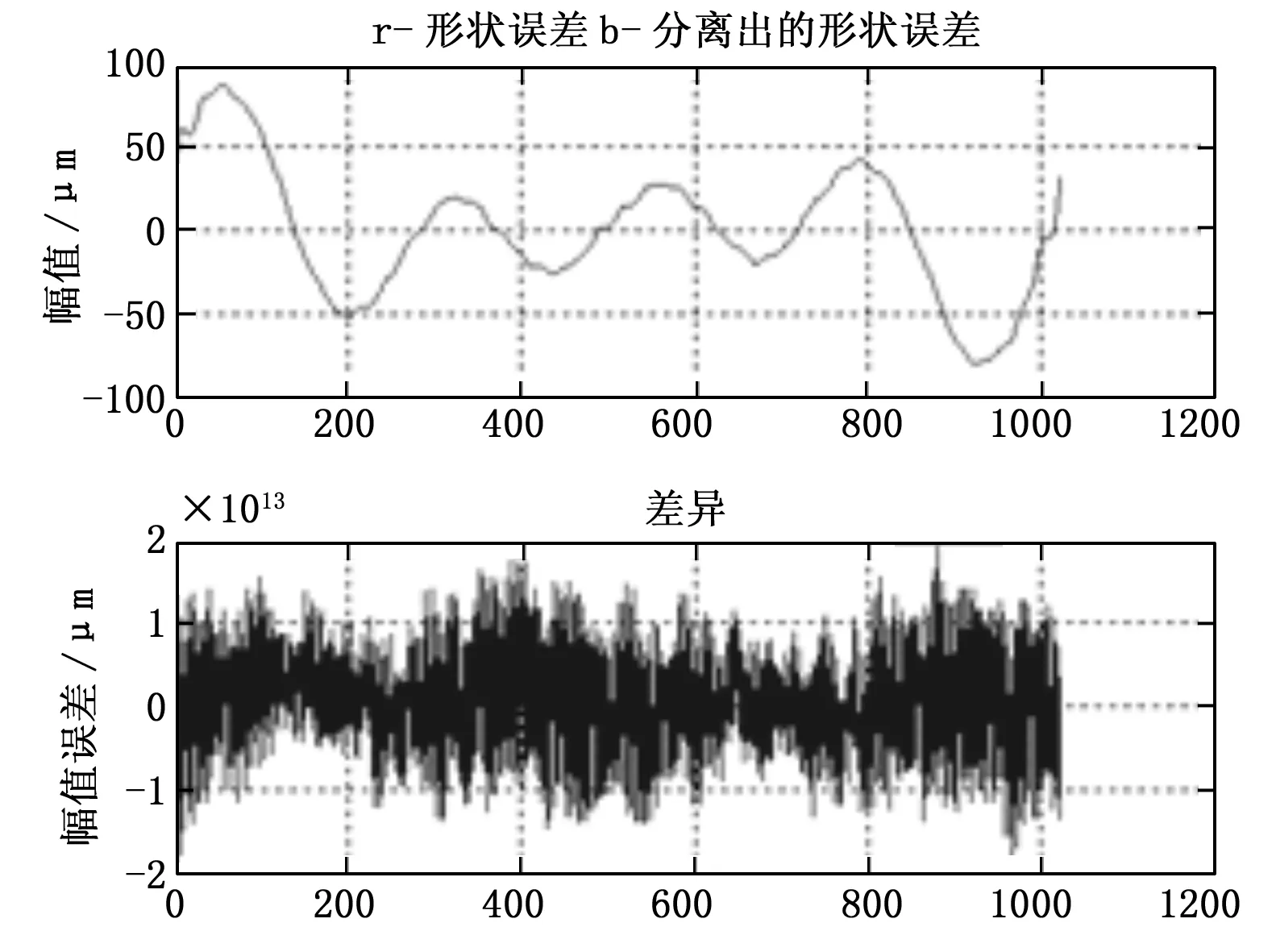
图6 α=90°,β=158°圆度误差设定与分离结果
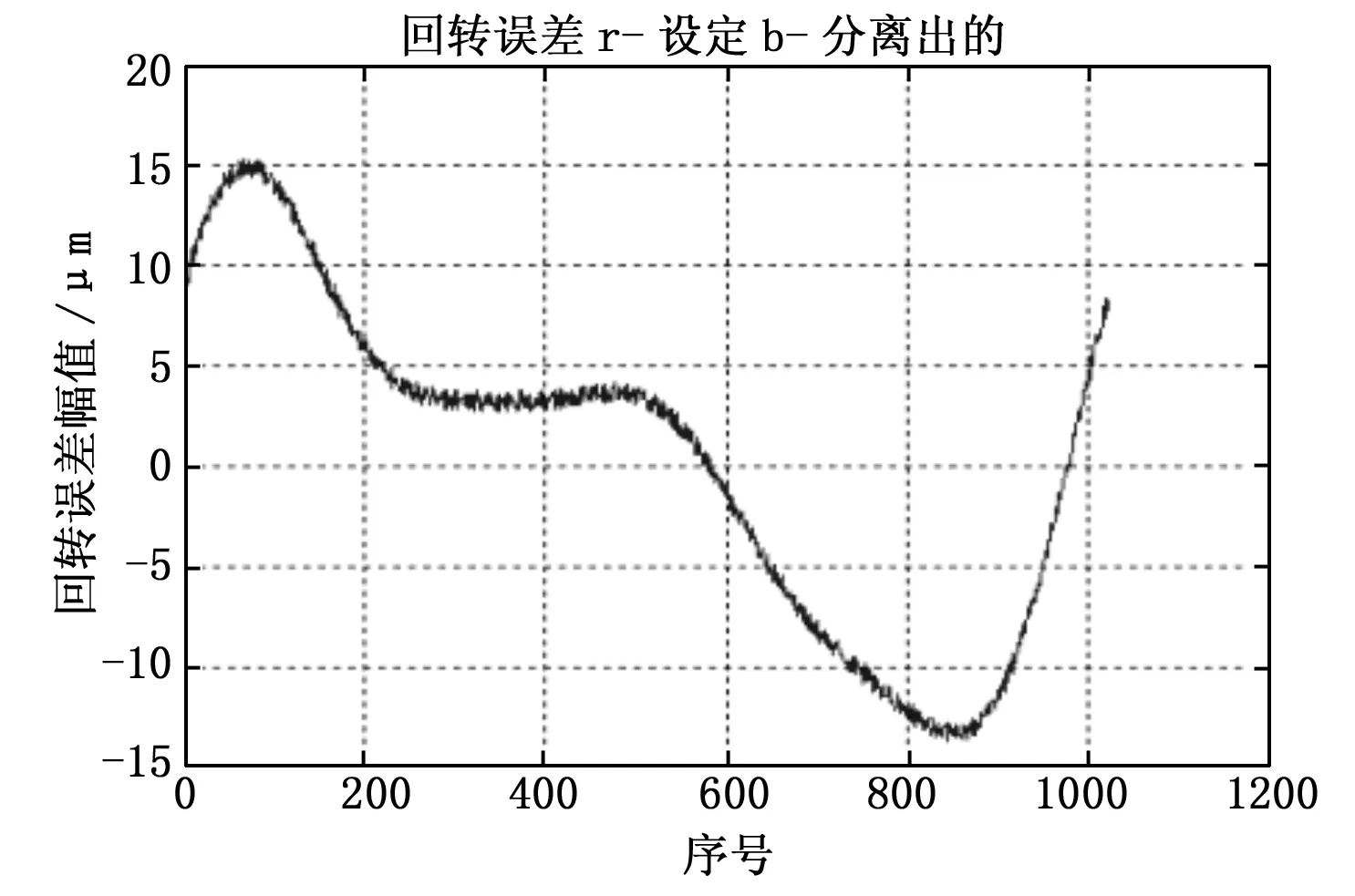
图7 α=90°,β=158°回转误差设定与分离结果
仿真表明,在实际安装夹角α、β偏离理想安装夹角±1°时,安装夹角的偏差δα、δβ对主轴圆度误差与径向回转误差分离有一定影响,但影响较小,圆度误差分离误差量级通常在10-13以上,可忽略。其中,仅在α=90°、β=156°时圆度误差的分离误差达到了0.03 μm左右,这是由于安装夹角引起的分离过程谐波抑制,多次仿真发现,这种谐波抑制现象引起的分离误差最大均控制在0.05 μm以下,这对于本项目的主轴径向回转误差分离影响较小可忽略。因此,在实际测微仪安装时可适度降低安装精度,允许一定安装角度偏差,并可根据角偏差的不确定度评估出主轴圆度误差和径向回转误差的分离不确定度。
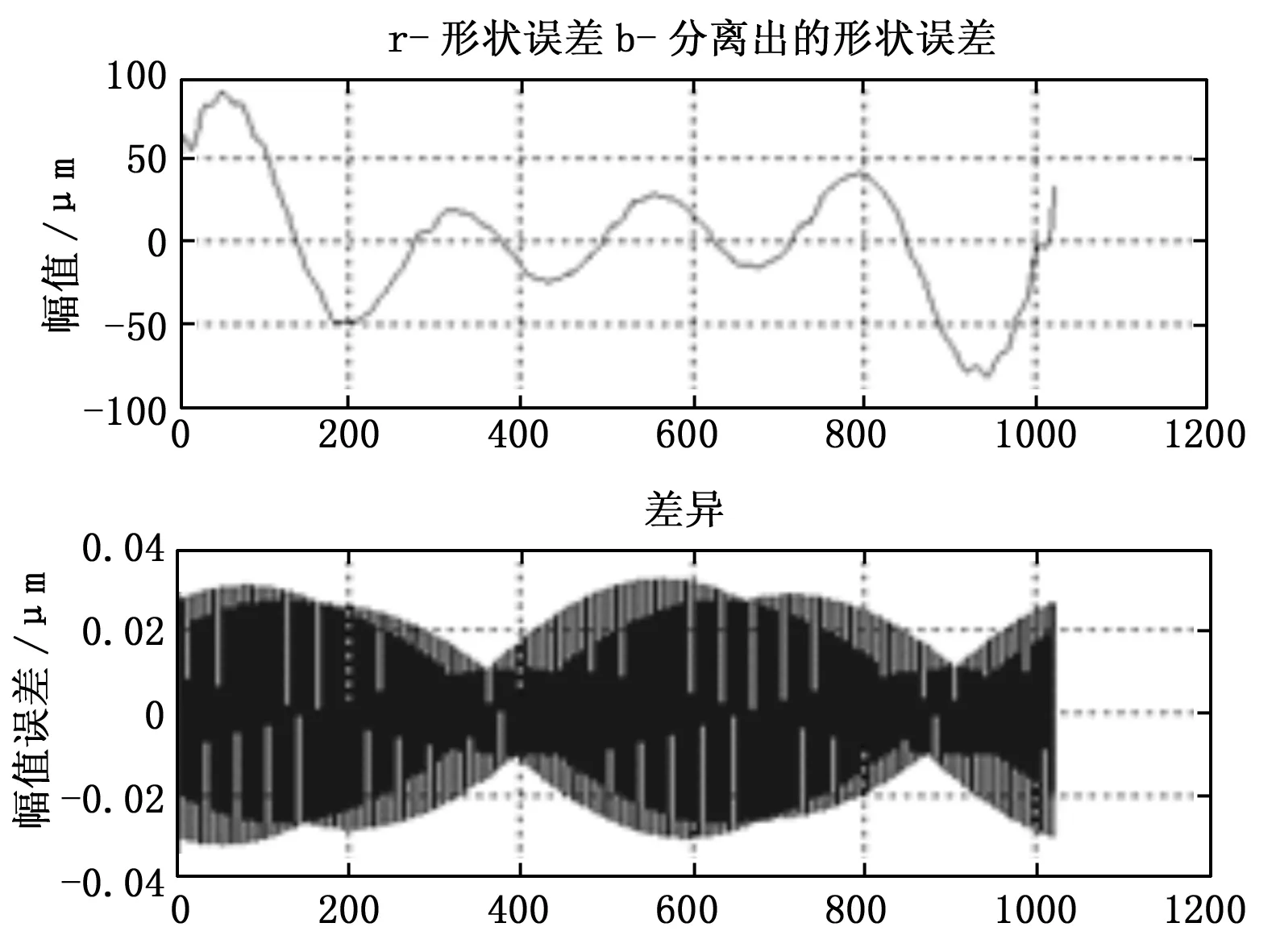
图8 α=90°,β=156°圆度误差设定与分离结果

图9 α=90°,β=156°回转误差设定与分离结果
综合各种因素,本项目三测微仪的安装角度分别为0°、90°和157°。
2.3 测试系统本底噪声对回转误差测试影响仿真
设测试系统带来的随机误差的统计幅值分别为0 μm、1 μm,仿真主轴径向回转误差分离的仿真结果,如图10~图11所示。

图10 随机噪声为0 μm时回转误差分离仿真图
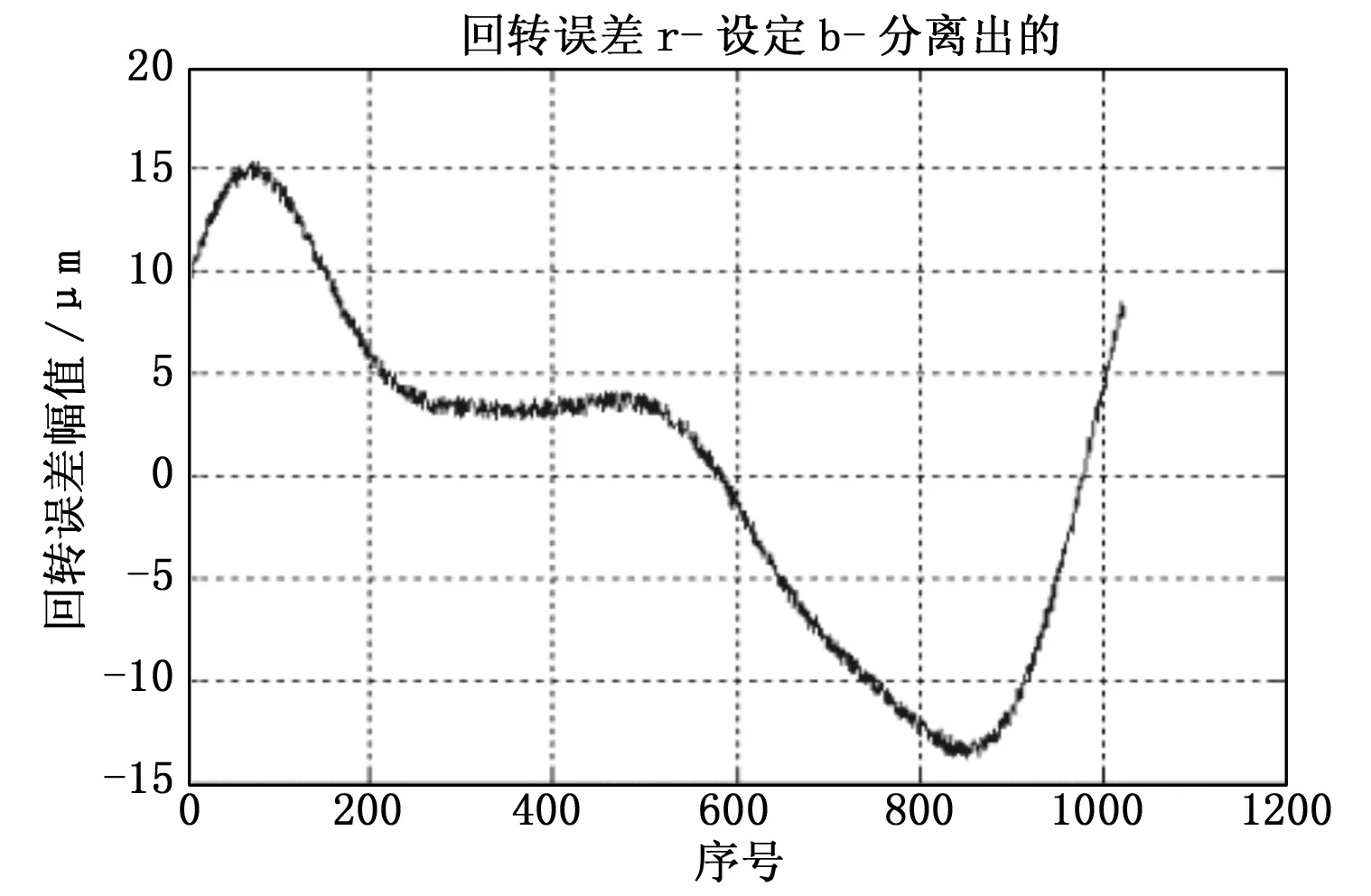
图11 随机噪声为1 μm时回转误差分离仿真图
由图11图12可知,测试系统的随机噪声将直接耦合到最终分离出的回转误差信号中。因此,在工程测试系统设计时,应尽量减小测试本底噪声,本项目采用24位A/D采集系统,本底噪声控制在400 μV左右,折合为距离为0.01 μm,满足工程需求。
3 实际测试效果
实测用三只量程为250 μm的电容测微仪,安装在精密离心机同加速度计安装定位平台同一水平面内的主轴周围,安装角度为0°,90°,157°,在稳定转速下,对主轴全周采集N=1 600点,执行三点法分离算法,精密离心机G值范围为1 g~100 g,转速最大为300 rpm,主轴回转误差与圆度误差分离效果如图12所示。转速为300 rpm时,主轴回转误差最大值为0.25 μm,圆度误差最大为4 μm。
4 结论
本文介绍了高精度精密离心机主轴回转误差的三测微仪测试法,对电容测微仪安装角度误差、主轴全周采样点数N以及测试系统本底噪声对主轴圆度误差与回转误差的影响进行仿真分析,仿真表明,N值越大,回转误差分离精度越高;测微仪安装角度误差可能导致分离谐波抑制,但对转速低于300 rpm,谐波抑制情况较少,大部分圆度误差分离误差达10-13量级;测试系统本底噪声对分离后的回转误差影响较大,对圆度误差影响较小。根据仿真结果,确定工程测试参数,实现了主轴回转误差0.25μm测量结果。

图12 转速300 rpm主轴回转误差与圆度误差实测图
[1] 凌明祥.精密离心机加速度测量模型研究[R].国防科研报告,GF-A0162889G,2012,03.
[2] 任顺清,杨亚非,吴广玉.精密离心机主轴回转误差对工作半径的影响[J].哈尔滨工业大学学报,2007, 32(1):54-57.
[3] 任顺清,陈 岩,赵振昊.精密离心机主轴回转误差对加速度计输入精度的影响[J].中国惯性技术学报,2007,15(1):116-119.
[4] 王怀兴.基于Labview的示波器仿真实验程序设计[J]. 培训与研究,2008,25(8):80-81.
[5] 张景和,冯晓国,刘 伟.用反向法测轴系回转误差[J].光学精密工程,2001,9(2):155-158.
[6] 张宇华,王晓琳,张国雄,等.多点法圆度及轴系误差分离方法的若干问题[J].北京理工大学学报,1999,19(3):309-313.
[7] 洪迈生,蔡 萍.多步法误差分离技术的比较分析[J].上海交通大学学报,2004,38(6):877-881.
[8] 张 明.空气静压主轴回转误差测量技术研究[D].绵阳:中国工程物理研究院,2008.
[9] 雷贤卿.基于误差分离的圆柱度精密测量技术研究[D].西安:西安理工大学,2007.
Research on Spindle Rotary Error Test Simulation Technique of Precision Centrifuge
Zhang Rong, Niu Baoliang,Ling Mingxiang, Wang Jue, Zhou Jikun
(Institute of Systems Engineering, CAEP, Mianyang 621900 China)
The rotary error of precision centrifuge affects directly dynamic radius measurement, the acceleration precision outputted by precision centrifuge and the safety of spindle working, it must be measured accurately. The application of capacitance micrometer test with three-point method to separate rotary error and roundness error is introduced. Also, the installation angle error of three capacitance micrometers, the sampling numbers of spindle lap and the test system background noise influence rotary error measurement result are simulated in MATLAB. The influences to rotary error separation caused by sampling N, δα, δβ and noise of test system are obtained. Thus, several technique parameters in rotary error test for 10-6level high precision centrifuge are certified. This technique has been applied to the spindle rotary error test of high precision centrifuge, the measurement result shows that using this measurement technique, the pure rotary error of spindle is 0.25 μm within speed of 300 rpm, the measurement result satisfies the requirement of the high precision centrifuge technique indicators.
precision centrifuge;rotary error;roundness error;three-point method; capacitance micrometer
2016-01-05;
2016-01-29。
国家重大科学仪器专项(2011YQ130047)。
张 荣(1979-),男,四川资阳人,工学硕士,高工,主要从事环境试验技术、动态测试技术以及计算机软硬件开发技术研究。
1671-4598(2016)06-0072-05
10.16526/j.cnki.11-4762/tp.2016.06.020
TP751
A

