一类微生物间歇发酵过程的参数辨识

徐恭贤，谭雯心，王佳星

(渤海大学 数理学院，辽宁 锦州 121013)



一类微生物间歇发酵过程的参数辨识

徐恭贤，谭雯心，王佳星

(渤海大学 数理学院，辽宁 锦州 121013)

针对甘油间歇发酵过程的参数辨识问题，首先建立了以各代谢物的浓度误差与斜率误差之和为目标函数的参数辨识动态优化模型，然后将其近似转化为静态非线性规划问题，最后应用遗传算法求解上述得到的非线性优化问题，并与已有文献进行了结果比较分析。

参数辨识；间歇发酵过程；优化模型；遗传算法

1，3-丙二醇具有广泛的应用领域，如聚合材料的单体、化妆品、润滑剂、医药等。1，3-丙二醇的生物合成尤其在工业领域有潜在价值，这主要是因为1，3-丙二醇成本低且无污染[1-3]。近年来，国内外专家学者对微生物发酵法生产1，3-丙二醇过程的数学建模、非线性分析、参数辨识、过程优化与过程控制等方面进行了广泛研究，取得了一系列成果[4-16]。例如，修志龙等[4]对过量动力学模型进行了修改，定性地描述了实验中的多态现象。Sun等[5]基于前人工作，建立了甘油生物歧化为1，3-丙二醇过程的还原途径酶催化动力学。Chen等[6]研究了一种转基因克雷伯氏杆菌发酵生产1，3-丙二醇的代谢途径。文献[7-11]研究了间歇发酵、连续发酵和批式流加发酵等甘油生物歧化过程的参数辨识问题。针对生物过程的不确定性问题，Xu等[12]应用H∞控制方法，设计了一个使甘油连续生物歧化过程在产物1，3-丙二醇体积产率最大的、最优稳态附近工作的鲁棒控制器。Zhu等[13]应用μ分析工具，设计了一个可用于甘油连续生物歧化为1，3-丙二醇过程的鲁棒控制器。Xu等[14]提出了一种可用于甘油连续生物歧化过程在有对象/模型不匹配和有输入约束条件下的在线迭代稳态优化控制策略。Xu等[15]研究了甘油连续生物歧化过程的多目标优化。

本文针对甘油间歇发酵生产1，3-丙二醇过程的参数辨识问题，建立了与其特点相适应的参数辨识优化模型，并为其设计了有效的求解方法，取得了较好的应用效果。

1　甘油间歇发酵过程

甘油间歇发酵生产1，3-丙二醇过程的物料平衡可由下列方程式计算[4]：

(1)

(2)

(3)

(4)

(5)

其中：t为发酵时间(h)；X为生物量(g/L)；CS为甘油浓度(mmol/L)；CPD、CHAc和CEtOH分别为产物1，3-丙二醇、乙酸和乙醇的浓度(mmol/L)；μ、qS、qPD、qHAc、qEtOH分别为细胞比生长速率、甘油比消耗速率、产物1，3-丙二醇、乙酸和乙醇的比生成速率(mmol/(g·h))，其动力学方程由式(6)～式(10)给出：

(6)

(7)

(8)

(9)

(10)

2　甘油间歇发酵的参数辨识模型

(11)

然后以各代谢物的浓度误差与斜率误差之和为目标函数，建立了如下甘油间歇发酵过程的参数辨识优化模型：

(12)

(13)

μ(x,p)≥0

(14)

qS(x,p)≥0

(15)

qPD(x,p)≥0

(16)

qHAc(x,p)≥0

(17)

qEtOH(x,p)≥0

(18)

(19)

3　参数辨识模型的求解方法

为了有效求解参数辨识问题(12)～(19)，本文首先利用修正配置法[17]将式(13)近似表示为如下代数方程：

xi(tj)=xei(tj-1)+0.5(tj-tj-1)·

(fi(xe(tj),p)+fi(xe(tj-1),p))，

i=1,2,…,5,j=1,2,…,Ns

(20)

则可将式(12)～(19)转化为如下非线性规划问题：

(21)

s.t.xi(tj)=xei(tj-1)+0.5(tj-tj-1)·

(fi(xe(tj),p) +fi(xe(tj-1),p)),

i=1,2,…,5,j=1,2,…,Ns

(22)

μ(x,p)≥0

(23)

qS(x,p)≥0

(24)

qPD(x,p)≥0

(25)

qHAc(x,p)≥0

(26)

qEtOH(x,p)≥0

(27)

(28)

式(21)～(28)可进一步化为如下只含变量上下界约束的形式：

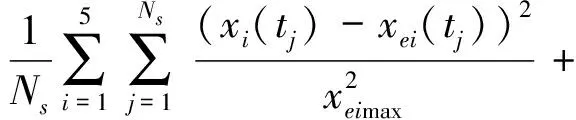
(29)

(30)

其中：ρ>0为罚系数；zi(x,p)(i=1,2,…,5)具有如下形式：

zi(x,p)=xi(tj)-xei(tj-1)-

0.5(tj-tj-1)(fi(xe(tj),p)+

fi(xe(tj-1),p)),

i=1,2,…,5;j=1,2,…,Ns

然后由下式求得点t1+rl(r=0,1,2,…,NK-2) 处的斜率(记为dis，s=1,2,…,NK)：

(31)

其中：

ei=(di1,di2,…,diNK,xi(t1))T

xei=(xei(t1),xei(t2),…,xei(tNs))T

这里的A和e是对

进行数值积分

后得到的，即A=(Ajs)Ns×NK，e是元素为1的列向量。

4　结果与分析

本文应用Matlab软件中的遗传算法求解优化问题(29)～(30)，各参数设置如下：遗传算法中的参数取默认值；罚系数ρ取值为108。表1给出了参数pk(k=1,2,…,16)的下界和上界。

表2为本文辨识方法获得的最优参数。表3给出了本文辨识方法与已有文献[19]的结果比较。从表中可以看出：本文方法的各代谢物的浓度误差与斜率误差之和比文献[19]小，约为文献[19]误差值的50.81%，这说明本文方法的参数辨识结果要好于文献[19]。

图1给出了本文辨识方法得到的主要产物 1，3-丙二醇的计算值与实验数据之间的比较，从图中可以看出，计算值与实验值吻合性较好。

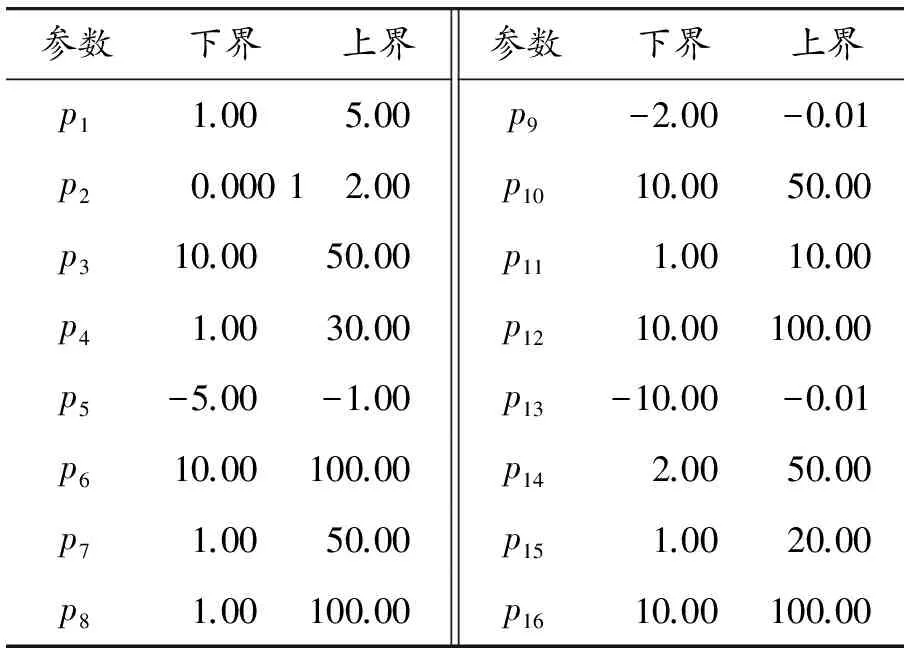
表1　参数的下界和上界

表2　最优参数值

表3　与已有文献的结果比较

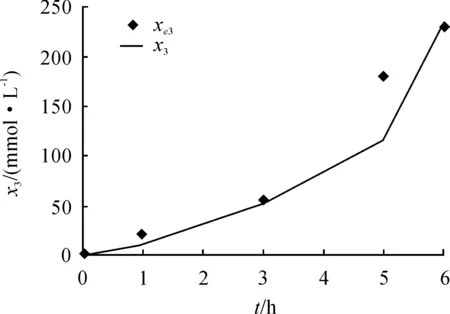
图1　主要产物1，3-丙二醇的计算值与实验数据的比较

5　结束语

本文针对甘油间歇发酵生产1，3-丙二醇过程的参数辨识问题，建立了与其特点相适应的参数辨识优化模型，并为其设计了有效的求解方法。与已有的参数辨识结果相比，采用本文方法得到了较小的代谢物浓度误差与斜率误差之和，相比原误差值降低了49.19%。

[1]ZENG A P，BIEBL H.Bulk chemicals from biotechnology:the case of 1，3-propanediol production and the new trends[J].Advances in Biochemical Engineering Biotechnology，2002，74:239-259.

[2]陈坚，刘龙.多级生物加工系统优化原理与技术[M].北京:化学工业出版社，2013.

[3]徐恭贤，邵诚，钱伟懿.非线性生化过程的优化和控制[M].北京:科学出版社，2015.

[4]修志龙，曾安平，安利佳.甘油生物歧化过程动力学数学模拟和多稳态研究[J].大连理工大学学报，2000，40(4):428-433.

[5]SUN Y Q，QI W T，TENG H，et al.Mathematical modeling of glycerol fermentation by Klebsiella pneumoniae:Concerning enzyme-catalytic reductive pathway and transport of glycerol and 1，3-propanediol across cell membrane[J].Biochemical Engineering Journal，2008，38(1):22-32.

[6]CHEN Z，LIU H J，LIU D H.Metabolic pathway analysis of 1，3-propanediol production with a genetically modified Klebsiella pneumoniae by overexpressing an endogenous NADPH dependent alcohol dehydrogenase[J].Biochemical Engineering Journal，2011，54(3):151-157.

[7]YUAN J L，ZHU X，ZHANG X，et al.Robust identification of enzymatic nonlinear dynamical systems for 1，3-propanediol transport mechanisms in microbial batch culture[J].Applied Mathematics and Computation，2014，232:150-163.

[8]SHEN B Y，LIU C Y，YE J X，et al.Parameter identification and optimization algorithm in microbial continuous culture[J].Applied Mathematical Modelling，2012，36(2):585-595.

[9]GAO K K，ZHANG X，FENG E M，et al.Sensitivity analysis and parameter identification of nonlinear hybrid systems for glycerol transport mechanisms in continuous culture[J].Journal of Theoretical Biology，2014，347:137-143.

[10]沈兰，李丹，胡昌华,等.抗烟草青枯菌菌株的分离、鉴定和发酵条件研究[J].西南大学学报(自然科学版)，2014(10):64-69.

[11]王丽，郝友进，何正波,等.高效溶栓菌株的筛选鉴定及发酵条件优化[J].重庆师范大学学报(自然科学版)，2013，30(3)：121-126.

[12]XU G X，SHAO C，XIU Z L.H∞control of bio-dissimilation process of glycerol to 1，3-propanediol[J].Acta Automatica Sinica，2006，32(1):112-119.

[13]ZHU X，YUAN J L，WANG X Y，et al.μ-synthesis of dissimilation process of glycerol to 1，3-propanediol in microbial continuous culture[J].World Journal of Microbiology and Biotechnology，2014，30(2):767-775.

[14]XU G X，SHAO C，XIU Z L.Optimizing control of dissimilation process of glycerol to 1，3-propanediol[J].Chinese Journal of Chemical Engineering，2008，16(1):128-134.

[15]XU G X，LIU Y，GAO Q W.Multi-objective optimization of a continuous bio-dissimilation process of glycerol to 1，3-propanediol[J].Journal of Biotechnology，2016，219:59-71.

[16]刘中利.白酒酿造发酵中基于智能策略的温度优化控制[J].重庆理工大学学报(自然科学)，2014(7):92-96.

[17]TSAI K Y，WANG F S.Evolutionary optimization with data collocation for reverse engineering of biological networks[J].Bioinformatics，2005，21(7):1180-1188.

[18]LUBANSKY A S，YEOW Y L，LEONG Y K，et al.A general method of computing the derivative of experimental data[J].AIChE Journal，2006，52(1):323-332.

[19]王明美.甘油间歇生物歧化过程的参数辨识[D].锦州：渤海大学，2015.

(责任编辑杨文青)

Parameter Identification for a Class of Microbial Batch Fermentation Process

XU Gong-xian, TAN Wen-xin, WANG Jia-xing

(College of Mathematics and Physics, Bohai University, Jinzhou 121013, China)

A dynamic optimization model for parameter identification of batch fermentation process of glycerol was first established. Its objective function is the sum of the least-square error and slop error of all metabolite concentrations. Then the proposed dynamic optimization model was transformed into a static nonlinear programming problem. Finally, a genetic algorithm was applied to solve the obtained nonlinear optimization problem. A comparation between the attained and exiting results was presented.

parameter identification; batch fermentation process; optimization model; genetic algorithm

2016-05-20

国家自然科学基金项目(11101051, 11371071); 辽宁省自然科学基金项目(2015020038); 辽宁省高等学校创新团队支持计划项目(LT2014024)；辽宁省大学生创新创业训练计划项目(201510167000012)

徐恭贤(1976—), 男, 辽宁庄河人, 博士, 副教授, 主要从事最优化方法与应用研究。

format：XU Gong-xian, TAN Wen-xin, WANG Jia-xing.Parameter Identification for a Class of Microbial Batch Fermentation Process[J].Journal of Chongqing University of Technology(Natural Science)，2016(10):76-80.

10.3969/j.issn.1674-8425(z).2016.10.012

O29

A

1674-8425(2016)10-0076-05

引用格式：徐恭贤，谭雯心，王佳星.一类微生物间歇发酵过程的参数辨识[J].重庆理工大学学报(自然科学)，2016(10):76-80.