夏热冬冷地区办公类建筑能耗预测模型研究

施剑锋，杨阳，马志荣

（安徽省安泰科技股份有限公司，安徽 合肥 230088）

夏热冬冷地区办公类建筑能耗预测模型研究

施剑锋，杨阳，马志荣

（安徽省安泰科技股份有限公司，安徽 合肥 230088）

办公类建筑的能耗预测是电力系统负荷管理的重要工作，实现高精度的预测对于电力系统运行的经济性和安全性具有重要意义。文章通过研究分析夏热冬冷地区办公建筑能耗的变化特点，建立神经网络建筑能耗预测模型，再通过大量数据构造样本集，运用软件对优化后的预测模型进行训练，并投入到某办公类建筑的预测实例中。结果表明，基于神经网络的建筑能耗预测模型的学习能力和预测能力较强，能较准确地实现办公类建筑的能耗预测。

夏热冬冷地区；神经网络；办公楼建筑；能耗预测模型

回归分析模型主要在大量数据的基础上，通过拟合获得对应的曲线，该曲线的外延趋势即可进行相应数值的预测。回归分析法的缺点是需要在大量的数据基础上进行预测分析，短期内较少的数据样本由于相对波动性较大，无法实现预测的准确性。此外，对于非线性的分析预测，虽然有非线性回归分析法，但实质上也是通过将非线性转换为线性关系后再进行的预测分析，所以预测结果往往误差较大。

弹性系数法作为一种间接性的预测方法，是指在对某个因素发展变化进行预测分析的基础上，利用弹性系数对另一个因素发展变化做出的分析预测。弹性系数法计算较为方便，且应用较为广泛。但此方法主要只考虑其中两个变量之间的关系，未能将其他相关的变量考虑进来，对于建筑类的能耗分析有一定片面性。

神经网络法是模拟人类思维的一种算法，该方法是基于人类大脑神经网络认识的基础上，人工构造的用以实现某种功能的计算方法。人工神经网络法先将相应数据信息用符号表示，并根据运算按照串行模式发送指令给计算机，进行进一步的逻辑推理。人工神经网络法具有分布式并行处理的能力，并可以自行开展学习和组织。更重要的是，对于数据样本较少，或者对象系统较为复杂的情况，该算法的非线性映射能力则能发挥优势，进行科学合理的分析预测。

Back Propagation神经网络即反向传播神经网络算法，简称为BP神经网络模型。该模型是目前应用广泛的神经网络模型，是一种误差逆向传播算法进行训练的多层前馈神经网络模型[1]。BP神经网络算法一般至少分为三层，即输入层、隐含层、输出层。其中，每层内的神经元互不相连，上下各层之间互相连接。该算法通过学习大量的输入、输出映射关系，使用最速下降法通过反向传播的方式不断进行网络阈值及权值的调整。同时，利用输出的误差值来推算估计输出层前导层的误差值，各层以此类推的反传并推算下去，从而获得网络各层的估算误差[2]。如下图1所示，为BP神经网络的结构示意图。

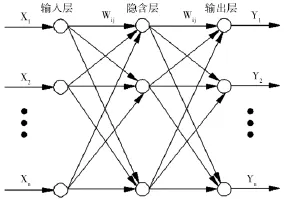
图1 BP神经网络结构示意图

输出隐含层：

输出输出层：

误差函数：

办公类建筑能耗所受的影响因素较多，根据建筑全寿命期的不同阶段，可分为设计阶段、建造阶段以及运营阶段。本文分析办公类建筑在运营使用过程中的能源消耗情况，且建筑使用过程中的能耗远远超出建造阶段的能耗[3]，所以主要考虑建筑运营阶段的影响因素对于模型的影响。

各因素与建筑能耗的关联系数［4］ 表1

结合国内外相关能耗模型影响因素的研究成果，根据灰关联分析建筑能耗与各类因素的关联程度，可得出各类因素的关联系数，见表1。根据分析的结构，按照灰关联度自高到低的顺序排列分别为：温度、湿度、天气特征、是否工作日、风速。根据相关领域的研究经验，默认灰关联度大于0.6的因素为主要影响因素[5]。同时，考虑到预测模型在实际应用中的可操作性，由于湿度暂时无法实现预报，故对于本文中的建筑能耗研究模型影响因素的选取为：最低温度、最高温度、天气特征以及是否工作日。

结合BP神经网络的模型结构，选择上述四项主要影响因素作为能耗模型的输入，建筑能耗作为输出，如图2所示。

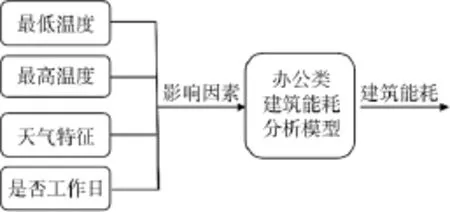
图2 办公类建筑能耗主要影响因素分析方案示意图

2.3.1 数据的选取

本文选取安徽某办公楼2014年5月和2015年5月，共计62天的能源监管平台已获取的数据作为样本。其中，随机选取其中50天的数据样本作为模型的测试数据，剩余12天的数据作为训练样本对模型进行训练。

2.3.2 归一化处理

在BP神经网络的学习训练过程中，由于各影响因子互不相同，且单位差异较大，使得各数据样本的向量数量级差别较大。为防止出现神经元达到过饱和状态，要对数据样本进行归一化处理，即将数据归化至[0,1]内[6]。归一化方法有很多种，本文采用计算公式如下：

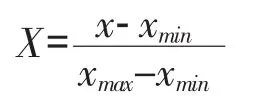
其中：X——归一化处理后的数据

x——样本数据

xmin——样本数据的最小值

xmax——样本数据的最大值

2.4.1 输入输出的确定

在网络模型中，需以向量的形式进行输入和输出。结合上文中能耗因素的选取，将最低温度、最高温度、天气特征以及是否为正常工作日的对应参数以向量的形式作为网络模型的输入。同样，对应的建筑能耗也以向量的形式作为输出。则改网络模型中的输入和输入项链分别为：

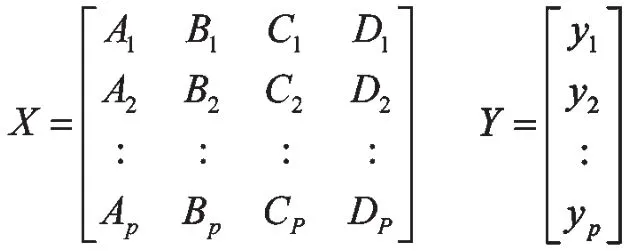
其中：A——最低温度

B——最高温度

C——天气特征

D——是否为正常工作日

y——建筑能耗值

p——样本数量

2.4.2 网络参数的确定

2.4.2.1 函数的确定

在BP神经网络的激活函数选择上，由于该项目的激活函数主要用于函数逼近，应选用线性函数[7]。此外，学习函数选取常用的梯度下降算法函数。

2.4.2.2 学习速率的确定

学校速率η的选取直接决定着收敛速度的快慢。通常选用较小的η进行计算，范围在0.01～0.7之间[8]，以确保系统的稳定性。本文的η选取0.1进行计算。

结合2016年5月的相关能耗影响参数，运用训练好的能耗模型，对于该办公楼2016年5月的能耗进行预测。相关分析结果包括：①预测能耗与实际能耗对比，如图3；②预测误差率统计，如图4；③能耗预测结果统计表，见表2。

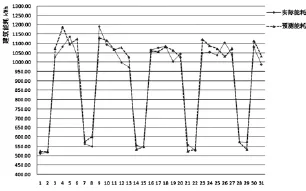
图3 预测能耗与实际能耗对比

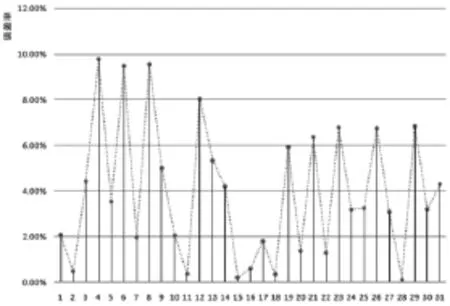
图4 预测误差率统计

能耗预测结果统计表 表2

通过上述预测能耗与实际能耗的对比结果可得，本文使用的模型预测误差率最大为9.77%，最小为0.11%，平均误率为3.92%，BP神经网络模型对该办公楼建筑的能耗预测较为精准。

为了进一步验证BP神经网络对该办公楼建筑的能耗预测的准确度，本文同时运用多元回归分析法进行能耗预测。在运用多元回归分析法进行建模的过程中，影响因子同样选取最低温度、最高温度、天气特征以及是否工作日，且使用与BP神经网络模型相同的样本值进行分析预测。相关分析结果包括：①预测能耗与实际能耗对比，如图5；②预测误差对比，如图6。

图5 预测能耗与实际能耗对比

图6 预测误差对比

通过上述预测能耗与实际能耗的对比结果可得，多元回归分析法建立的模型预测误差率最大为12.04%，最小为0.39%，平均误率为5.02%，相比较BP神经网络模型而言，预测误差较大。

本文依据BP神经网络法建立安徽某办公楼的建筑能耗预测模型，根据日建筑能耗的数据样本对网络模型开展训练并进行预测误差的分析，模型预测值与实际数据的平均误差率仅为3.92%，具有较高的预测精确度。研究结果证明，BP神经网络在模型的拟合度以及对办公建筑的能耗预测方面有较明显的优势，其非线性映射关系对变量的处理效果优于多元线性回归模型的线性关系，研究结果为办公类建筑以及其他公共建筑的能源管理工作提供了技术支撑和参考依据。

[1]张中昱.基于BP神经网络和模糊综合评价的环境分析评价系统[D].天津：天津大学，2006.

[2]何磊.基于BP神经网络的建筑能耗预测[J].浙江建筑，2008(12)：47-50.

[3]陈振，孙东威.影响我国建筑能耗的因素分析[J].产业与科技论坛，2008(6).

[4]刘长俊.基于遗传BP神经网络技术的大型公建能耗分析模型的研究与应用[D].南宁：广西大学，2012.

[5]张光华，傅志盛，田红光.造纸湿部因素灰关联分析法的适宜性研究[J].中国造纸学报，2000(17).

[6]王建国，吴美容.运用BP人工神经网络设计变形预报模型[J].矿山测量，2010(4)：73-75+4.

[7]闻新，周露，王丹力，熊晓英.MATLAB神经网络应用设计[M].北京：科学出版社，2000.

[8]阎平凡，张长水.人工神经网络与模拟进化计算[M].北京：清华大学出版社，2000.

TU201.5

A

1007-7359（2016）05-0056-03

10.16330/j.cnki.1007-7359.2016.05.014

施剑锋（1976-），男，江苏海门人，毕业于中国科技大学，学士；工信部高级项目经理，信息系统管理师，IPMP-C国际项目经理。