凸二次曲面的工艺球面补偿检测

陈 泽，胡明勇，赵 奇，范二荣



凸二次曲面的工艺球面补偿检测

陈 泽1,2，胡明勇3，赵 奇3，范二荣3

( 1. 中国科学院南京天文仪器研制中心，南京210042；2. 中国科学院大学，北京100049；3. 合肥工业大学光电技术研究院，合肥 230009 )

在非球面的检测中，工艺球面补偿检测是最普遍的方法。针对该方法适用范围的局限性，本文提出了应用工艺球面补偿检测时非球面所必须满足的条件。根据波像差理论和瑞利判据，推导出凸二次曲面能够应用工艺球面补偿检测所必须满足的条件，并采用有限距离正面补偿检测的方法，对工艺球面补偿检测的局限性提出了改进。最终结果表明本文所提出的理论能够判定，所需要研制的凸双曲面镜不能直接应用工艺球面补偿检测，而组合补偿检测方法能够保证凸双曲面的面形精度PV=0.159 8优于/6(=632.8 nm)，满足技术指标。

光学检测；瑞利判据；凸二次曲面；像差理论

0 引 言

目前，非球面镜的检测主要分为接触式检测和非接触式检测两大类。接触式检测中最常见的就是轮廓仪测量方法[1]。1856年，Fu Ke Lewin发明了刀口仪[2]。20世纪70年代，数字干涉仪的问世。这都使得在加工或是最终检测过程中非接触式的检测成为可能。非球面镜的光学检测方法直接决定了非球面镜的加工精度与加工效率。非球面镜的检测中，凸非球面的检测比凹非球面的检测更加复杂，主要是因为其需要有一束至少同等口径的会聚光束[3]才能够实现。在20世纪70年代Wyant等提出了计算全息图(Computer Generated Hologram，CGH)检测方法[4]，至今CGH检测方法得到了长足的发展，这对于凸非球面镜的检测具有划时代意义。但CGH方法检测大相对孔径的非球面镜时存在着全息干涉片加工困难，制造成本相对高昂[5]。此外，凸非球面镜的检测还有子孔径拼接法[6]，offner补偿器检测法[7]，工艺球面补偿检测法等。

工艺球面补偿检测方法无疑是凸二次曲面镜检测方法中最为方便，成本最低的一种方法。但是工艺球面补偿检测方法也有其适用条件以及应用范围，但遗憾的是迄今为止还没有任何文献对此进行过完善的分析。本文从波像差理论出发，提出了工艺球面补偿检测的波前像差的计算方法，分析了该检测方法能够得以应用而应该满足的条件，并在理论分析的基础上提出了工艺球面补偿检测方法的改进措施。

1 工艺球面补偿检测方法分析

1.1 以工艺球面为反射面的补偿检测方法

凸二次曲面镜的技术参数：全口径为500 mm，顶点曲率半径为900 mm，材料为熔石英，中心厚度为70 mm，圆锥系数2=1.05，面形精度要求PV≤/6。

工艺球面补偿检测如图1所示，即将非球面作为凸面，透镜的第二面加工为工艺球面，用球面的固有球差补偿非球面的法线像差。在非球面的有限元距离处放置点光源，工艺球面镀上反射膜，使得同等口径光束经过球面反射后沿原路返回在光源处形成干涉。

图1 工艺球面补偿检验

由图2所示的Ray fan曲线可以发现，经过设计优化后整个系统的球差峰值依然很大，特别是在入瞳0.8环带以后达到球差峰值，弥散斑达到了50 μm。由此可以发现，并不是任何凸二次曲面镜都可应用工艺球面补偿检测方法进行光学检测。

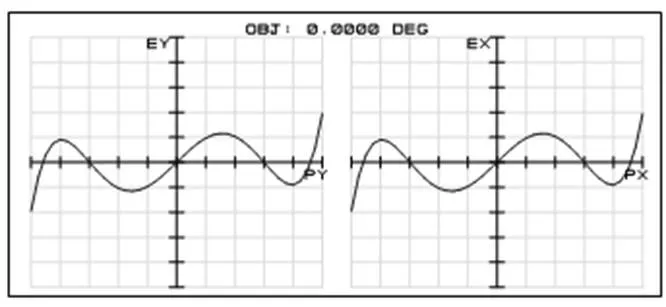
图2 工艺球面补偿检验的Ray fan曲线

1.2 工艺球面补偿检测方法的像差模型的建立

由一系列球面和非球面组成的光学系统，其球差表面分布系数[8]：

其中：表示表面序号；h表示第一近轴光线在第面上的高度；P为该表面的球差系数；e为二次曲面的偏心率；n表示第面前的折射率；u第面的第一近轴光线的入射角。如图3所示，非球面为透射面，工艺球面为反射面，求出三级球差的表达式。各个参量的表达式：

式中：0为图中非球面顶点曲率半径。根据近轴光路角度公式：

式中：R表示相应序号表面的曲率半径，若该表面为非球面，则表示为顶点曲率半径，所以0=1。令=1，将式(2)中的参量代入式(5)中，整理上式可得：

对于补偿检测系统，光源处于有限远距离，初级轴上球差为[8]

由式(6)可得1/，将其带入式(8)中，波像差可表示为圆锥系数2和非球面镜的相对孔径=2/0的表达式：

根据瑞利判据可知，光学系统的波像差小于/4时，可以认为光学系统成像是完善的。所以，检测凸二次曲面镜的面形的光学系统的波像差必须小于/4，即凸二次曲面镜的检测光学系统完善成像。在实际光学系统中，波像差的大小会随着高斯像点附近的参考点的选择而异，所以总能在高斯像点附近找到一个位置，使得光学系统的波像差最小，而这个使得波像差最小的位置就是成像的最佳焦点位置。波像差推导过程中只考虑了光学系统的初级像差，对于这样的光学系统，最佳焦点位置应该在处，而边缘带球差为零，其最大剩余波像差在0.707环带上[8]。所以波像差的表达式改为

1.3 工艺球面补偿检测的适用性判断

以工艺球面为反射面，采用正向光路进行计算(即光线的方向为从左到右)。取透镜的口径为=500 mm，透镜材料为熔石英，折射率=1.458 6。一般采用4干涉仪进行检测，检测波长为=632.8 nm。经过计算可以发现，若将2的具体数值带入能够得出合理解的实数解。消去式(6)中的，得到关于的表达式，如下所示：

综上所述，对于任意参数的凸二次曲面镜，若采用工艺球面补偿检测，检测系统的波像差需满足瑞利判据，则凸二次曲面镜的参数必须满足式(10)、式(12)以及的取值。这也是判定不同圆锥系数和相对孔径的凸二次曲面镜能否采用工艺球面补偿检测的理论依据。由此可得：

其中：为比例关系的修正值，因为关于波像差计算过程中的近似以及误差都可以通过的修正来使得理论值更加接近实际光线追迹的结果。现定义修正值，由式(11)求得的具体数值后，再计算其修正值。采用工艺球面补偿检测的凸二次曲面镜的圆锥系数2以及相对孔径的关系如图4所示，在曲线下半部分区域内的非球面都能够满足工艺球面补偿检测的条件。

在图4中，实线表示实际光线追迹的曲线，虚线表示理论分析曲线。两者之间的偏差主要在于，第一，理论推导过程中多次使用角度近似；第二，像差理论是在近轴光学的基础上得以完善，而当孔径角超过5°的时候，理论推导的误差也就不能忽略了。所以这就造成了理论与实际的偏差，修正值的提出，能够在一定程度上弥补这种偏差。经过计算可以发现，，工艺球面半径值无解，或者说没有合理的解。

根据1.1中凸二次曲面镜的技术参数，其点(2，)，即(1.05，0.555 6)，在曲线上方，不满足检测工艺球面补偿检测的条件。

2 工艺球面补偿检测方法的改进

2.1 有限距离正面补偿原理

根据图5所示，由光线的几何关系很容易得出前组凹透镜的焦距表达式：

利用方法求出前组透镜的结构参数。以无穷远物距的归一化特性参数表示有限远物距的归一化特性参数：

其中：2为透镜第二面的曲率值。对前组透镜的光焦度规一化，得到：

对于既定的球差值，将式(17)代入式(16)中，求得合理的透镜结构参数值，再结合式(17)和式(18)得出透镜表面的曲率半径：

2.2 检测系统设计及面形检测结果

由图5所示，可以将透镜看作薄透镜，设点至补偿透镜距离=1 200 mm，补偿透镜与待检测透镜间距=3 000 mm。设计时规定补偿透镜半口径1=50 mm，而2=250 mm。凸二次曲面镜的材料为熔石英，折射率=1.458 6。将参数代入式(2)、式(4)和式(6)可以分别求得：1=-0.066 6，=-0.626 4，Ⅰ=0.481 0。由于：

将和1代入式(20)中，求得1=592 2 mm，即是工艺球面的半径值。

再将所设定的参数代入式(14)中，计算可得前组透镜的焦距1=-2 000 mm。将所得的球差值和式(17)代入式(16)中，建立有关前组透镜的形状参数的方程：

前组补偿镜采用K9材料，其特性参数为：d=1.516 3，0=2.05，0=-1.25。经计算整理可得：

解得：=-15.214 4或者17.547 8，取=-15.214 4。代入式(19)中，得：前组补偿透镜，。

Zemax对计算出的透镜初始结构参数进行优化设计。4D干涉仪的激光波长=632.8 nm，而刀口仪的钠光波长=589.3 nm，优化设计过程采用多重结构，保证凸二次曲面镜在修磨阶段能够用刀口仪或干涉仪进行检测。将前端物距和补偿透镜至待检测透镜的间距设为补偿量，优化后的结构参数如表1所示。

图5 有限距离正面补偿检测光路图

表1 优化后的检测光路参数

Table 1 Data of light path after optimizing

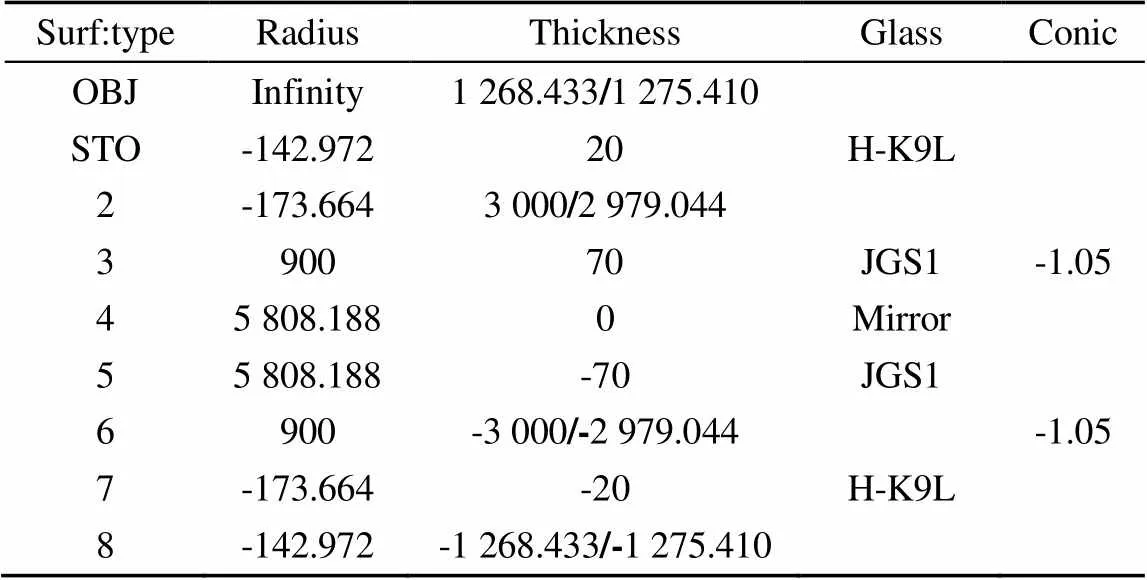
由图6和图7所示的检测系统波前像差不难发现，=632.8 nm干涉仪检测时，补偿方案的理论波像差PV=0.000 9，RMS=0.000 2；=589.3 nm刀口仪检测时，补偿方案的理论波像差PV=0.016 1，RMS=0.0035。设计结果优于凸二次曲面镜的技术要求，满足实际应用的需要。

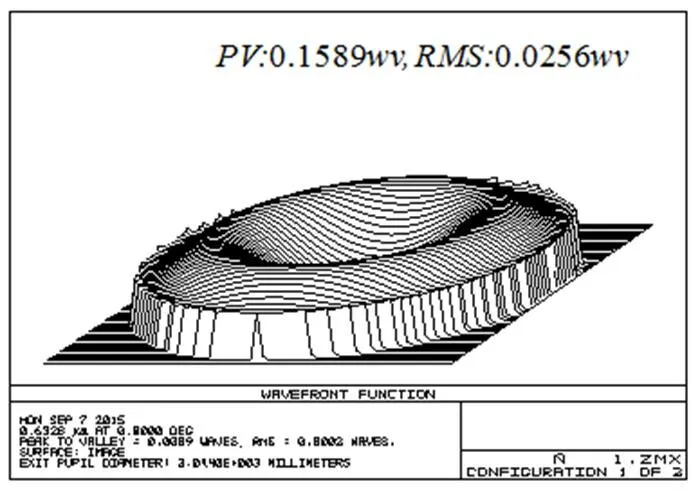
图6 检测系统波像差(λ=632.8 nm)

图7 检测系统波像差(λ=589.3 nm)

根据装配需求，对检测系统进行公差分析。为了更好的约束公差，将公差分析的RMS Wavefront值约束在/25以下。补偿镜和工艺球面的半径公差对补偿检测精度的影响远远没有间距和待检测元件的倾斜所带来的影响更大。所以，在加工补偿透镜和工艺球面的时候，规定其半径公差控制在1 μm以下，这对于成熟的球面加工工艺来说是很容易实现的。从公差分析来看，补偿镜的厚度、补偿镜和凸二次曲面镜之间的间距公差控制在1 μm以内，待检测元件的倾斜在0.000 5°以下，这两个因素都不仅仅是加工所能直接解决的，只能在凸二次曲面镜的检测过程中通过不断的微调来保证检测的精度。由此看来，为了降低系统的误差，第一需要保证补偿透镜和工艺球面的半径误差；第二，在检测过程中也依赖于完善的装调方案。加工完成后，利用4D干涉仪检测凸二次曲面镜的面形，如图8所示。PV=0.159 8，RMS=0.025 6，面形精度满足技术要求。

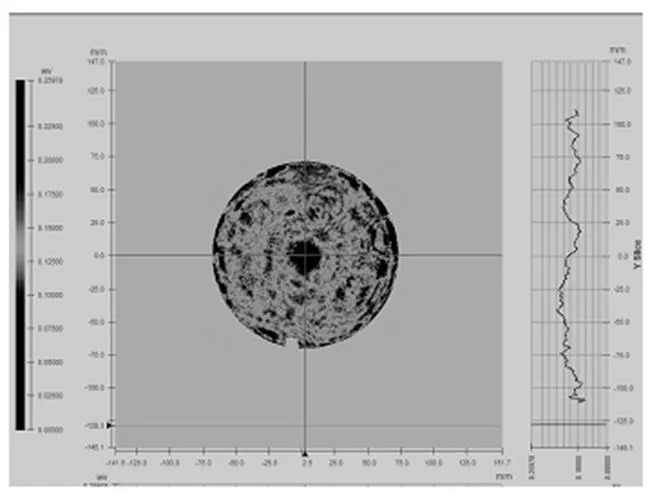
图8 凸双曲面镜的面形干涉图

3 结 论

确定凸二次曲面镜的口径及材料，如若满足前文所述的判定条件，凸二次曲面镜便可用工艺球面补偿的方法进行检测；如若不满足上述条件，根据波像差的大小选择合适的前组补偿透镜进行补偿检测。虽然上述判定条件存在一定的理论误差，文中所述的改进方法也不能作为凸二次曲面镜检测的完备方法，但是无论是从波像差概念出发的理论分析，还是对于传统工艺球面补偿检测方法的改进都为非球面检测的分析和设计提供了新的思路。

参考文献：

[1] 师途，杨甬英. 非球面光学元件的面形检测技术 [J].中国激光，2014，7(1)：26-46.

SHI Tu，YANG Yongying. Surface testing methods of aspheric optical elements [J].Chinese Journal of Lasers，2014，7(1)：26-46.

[2] 张钧，董军，张艳，等. 数字刀口检测技术 [J]. 光电工程，2005，32(5)：65-68.

ZHANG Jun，DONG Jun，ZHANG Yan，. Study on digital knife-edge test [J]. Opto-Electronic Engineering，2005，32(5)：65-68.

[3] 潘俊骅. 光学非球面的设计、加工与检验 [M]. 苏州：苏州大学出版社，2004：51.

PAN Junhua. Design，fabrication and testing of aspherical optical surface [M]. Suzhou：Soochow University Press，2004：51.

[4] 高松涛，隋永新，杨怀江. 用计算全息图对非球面的高精度检测与误差评估 [J]. 光学学报，2013，33(6)：0612003.

GAO Songtao，SUI Yongxin，YANG Huaijiang.High precise testing of aspheric with computer-generated hologram and error evaluation [J]. Acta Optica Sinica，2013，33(6)：0612003.

[5] 宋强，杨宝喜. 大口径凸非球面面形检测方法研究 [J]. 中国激光，2014，41(4)：0408003.

SONG Qiang，YANG Baoxi. Study on large covex aspherical lens testing [J]. Chinese Journal of Lasers，2014，41(4)：0408003.

[6] 王孝坤. 利用子孔径拼接法测量大口径凸面反射镜 [J]. 应用光学，2013，34(1)：95-100.

WANG Xiaokun. Large convex mirror measurement by subaperture stitching interferometry [J]. Applied Optics，2013，34(1)：95-100.

[7] 陈旭，刘伟奇，康玉思，等. Offner补偿器的结构设计与装调 [J]. 光学精密工程，2010，18(1)：88-93.

CHEN Xu，LIU Weiqi，KANG Yusi，. Design and tolerance analysis of offner compensator [J]. Optics and Presision Engineering，2010，18(1)：88-93.

[8] 张以谟. 应用光学：三版 [M]. 北京：电子工业出版社，2008：344-348.

ZHANG Yimo. Applied Optics：3nd Edition [M]. Beijing：Electronics Industry Press，2008：344-348.

[9] 袁旭沧. 现代光学设计方法 [M]. 北京：北京科学技术出版社，1995：79-81.

YUAN Xucang. Optical Design [M]. Beijing：Beijing Science and Technology Press，1995：79-81.

Compensation Testing of Technological Spherical Surface for Convex Quadric Surface

CHEN Ze1,2，HU Mingyong3，ZHAO Qi3，FAN Errong3

( 1. Nanjing Astronomical Instruments Research Center, Chinese Academy of Sciences, Nanjing210042, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China; 3. Academy of Photoelectric Technology, Hefei University of Technology, Hefei230009, China)

In the testing of aspheric surface, the method of spherical compensation testing is always applied widely. Referring to the limitation of this method, the conditions are put forward which the aspheric surface has to meet. According to aberration theory and Rayleigh criterion, we could get the principles of applying the spherical compensation testing method to test convex quadric surface. And according to the compensation tests with the beam incidence at a distance, we can improve the method of spherical compensation testing. After accomplishing the manufacture of convex quadric surface mirror, the finial consequence shows that the theory and practices in this article can determine that spherical compensation testing can not be used to the test of this convex hyperboloidal surface mirror andPVof the surface is 0.158 9which is better than/6 (=632.8 nm) under the use of combined compensation testing.

optical test; Rayleigh criterion; convex quadric surface; aberration theory

1003-501X(2016)09-0056-06

O435.2；TN247

A

10.3969/j.issn.1003-501X.2016.09.010

2015-09-25；

2016-03-01

陈泽(1991-)，男(汉族)，江苏扬州人。硕士研究生，主要研究工作是光学设计、加工及检测。E-mail：taijiguiyi@163.com。