一种毫米波调频连续波雷达的目标速度测量方法

完 诚

(中国船舶重工集团公司第723研究所，扬州 225001)



一种毫米波调频连续波雷达的目标速度测量方法

完 诚

(中国船舶重工集团公司第723研究所，扬州 225001)

提出了一种应用于地面监视的连续波雷达，使用线性调频连续波(LFMCW)波形产生和快速傅里叶变换信号处理技术进行地面运动目标检测。由于较短线性调频时间和高重复频率，目标的径向速度对测量的差频信号影响很小，因此采用多个线性调频连续波信号在各个距离门上测量径向速度。为了解决不模糊最大径向速度，提出了一种改变线性调频持续时间的方法。最后根据发射和接收信号的频差以及接收天线，也可以计算出目标距离和方位角。

调频连续波；差频；多普勒频率

0 引 言

相对于脉冲雷达，调频连续波雷达体积小,重量轻,结构简单,具有大时带积，因此应用在很多高测距精度和高距离分辨率的场景，比如安全防护、边海防护、海洋洋流特性研究等领域。本文研究的是一款应用于地面监视的调频连续波(FMCW)雷达系统，由于发射信号具有极短的线性调频时间TChirp，测量到的频差始终为正，因此雷达接收机中采用单接收通道即能满足应用需求，考虑到线性调频时间TChirp短并且有较宽的调制带宽，雷达回波信号中的多普勒频率fD对距离的影响在系统可以接受的范围内，因此利用发射信号和目标回波信号之间的频率差来确定目标距离，即使在多目标的情形下，也都可以计算出目标的实际距离。

然而在某些特殊场景下，对于运动目标多普勒频率的测量是模糊的[1]。因此，本文提出一种低复杂算法的解模糊方法，这种方法在多目标情形下也能够测量运动目标的距离R、径向速度vr和方位角φ。

1 系统构建与设计

地面监视雷达的波形产生输出一定带宽的锯齿波调频信号功分放大后，通过发射天线对外发射连续波探测信号。探测目标信号经接收天线送到接收机后最终得到差频信号，该差频信号包括目标的距离和速度信息，再进行快速傅里叶变换以实现目标距离、径向速度的测量。同时通过接收天线的方位信息，可以计算出目标方位角。

1.1 波形产生与差频分析

连续波雷达最常见的线性调频(Chirp)波形为锯齿波，本文中雷达波形产生器产生的是一段标准FMCW锯齿波信号，该波形中的线性调频持续时间很短，在线性调频持续时间(TChirp)内，FMCW雷达通过发射天线对外发射频率从f0至f0+fsweep之间连续变化的线性调频信号，目标反射的回波信号在延时τ后到达接收天线，如图1所示。

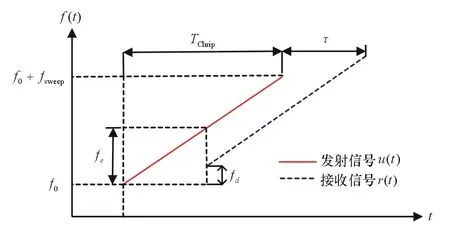
图1 单调频周期的发射信号和接收信号

雷达的发射波形u(t)可用解析形式表示为：

(1)

式中:ATx为信号幅度；ΦTx(t)为瞬时发射信号相位,可通过下式计算得出：

(2)

接收目标回波可由下式表示：

(3)

式中：信号相位ΦRx(t)可表示为：

(4)

为了便于分析，将发射信号振幅ATx和接收信号振幅ARx归一化为ATx=ARx=1。通过瞬时发射信号对接收信号进行下变频，再经过低通滤波后可获得差频信号e(t)，表示如下：

(5)

发射信号和目标回波信号间的差频fe受目标距离R0和径向速度vr的影响，其解析形式可表示如下：

(6)

式中：fD为多普勒频率。

考虑L个连续调频周期信号，各信号持续时间均为TChirp[2]，如图2所示。

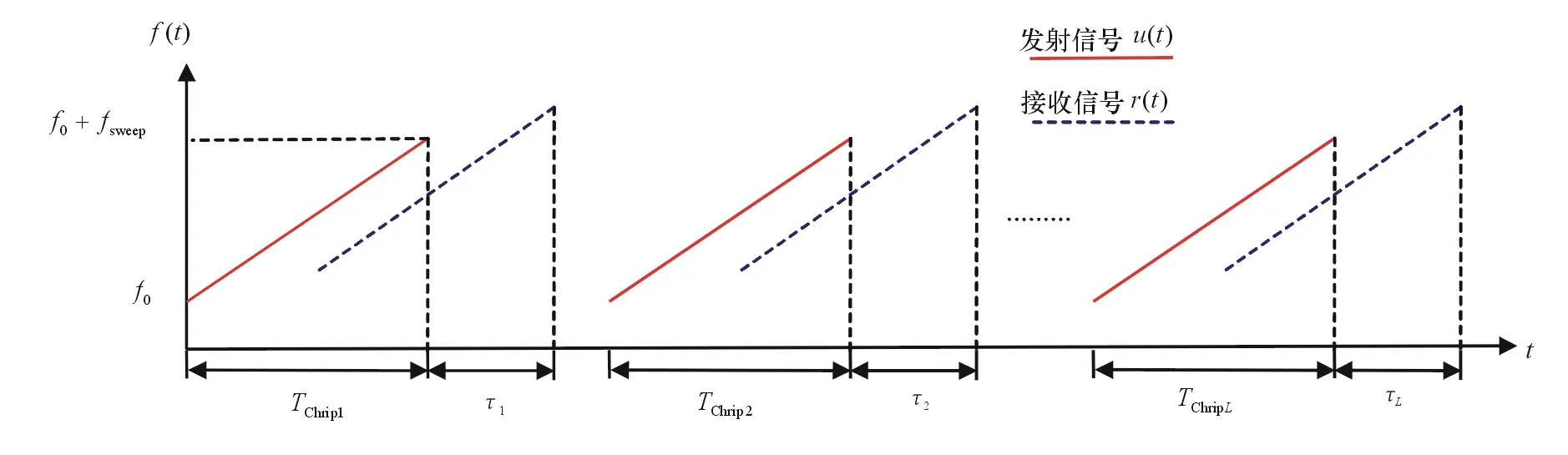
图2 L个调频周期的接收和发射信号

时间离散的差频信号可由下式描述：

(7)

1.2 信号的FFT处理

差频信号在信号处理单元的处理过程如图3所示。

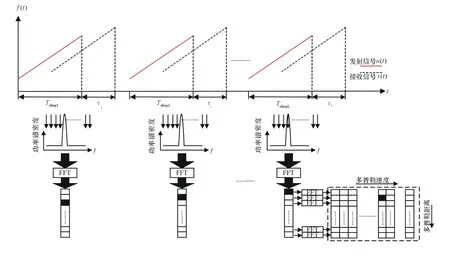
图3 连续Chirp的距离和多普勒处理过程

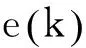
2 解多普勒频率模糊

2.1 Chirp持续时间的改变

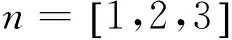
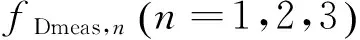
2.2 解模糊算法

解模糊算法可以按照下面的步骤进行，如图4所示。

(1) 初步目标探测：在第一信号块中进行单探测，形成单列探测点迹。

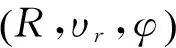
(3) 最终目标探测：将候选点迹估计的信噪比与门限T作比较。据此选定最终点迹j。

SNR≥T

(8)

如果信噪比大于门限T，则认为检测到了目标[6]。

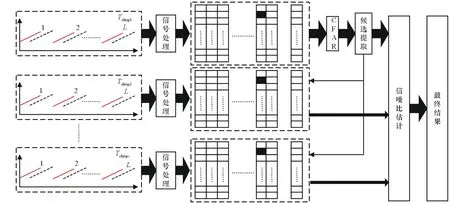
图4 解模糊目标算法

3 仿真与分析

下面对二维FFT和解多普勒模糊进行仿真分析，假设两目标车辆都位于距离R0=1 km处，径向速度为vr=17 m/s，该值大于雷达系统最大不模糊速度范围。2个目标唯一的不同之处在于它们的方向角位置：第1个目标的方向角假定为φ1=10°，第2个假定为φ2=-10°。

信号处理对于每个调频周期内的目标回波信号分别进行2次FFT转换。根据检测各距离、速度分辨单元的幅度值大小来确定目标的距离、速度信息。

图5表明了雷达检测到单个目标幅值最大的点所在的位置求得车辆的距离和速度。其中，由于目标径向速度大于最大可探测径向速度vmax，因而无法计算其真实速度值。

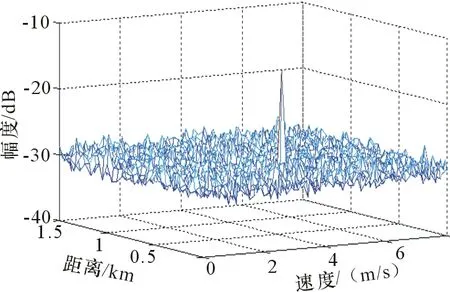
图5 基于单信号块的距离速度测量

图6描述了利用M个接收天线信号对2个目标速度与方位进行仿真得出的测量结果，明确表明了方位角不同的2个目标。

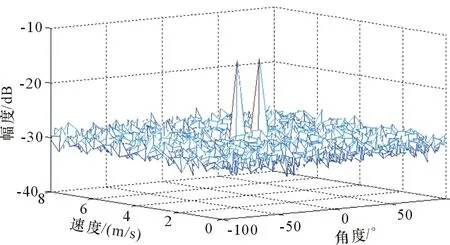
图6 2个目标的速度角度测量

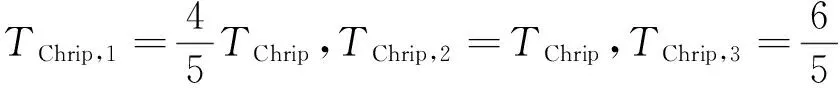
可以观察到峰值相同的分辨单元为61.2 km/h=17 m/s，均大于信噪比门限，为真实的径向速度。

4 结束语

本文提出了一种线性调频FMCW波形的设计方法，介绍了接收天线和扩展不模糊多普勒测量范围的方法，进而对带通信号进行二维快速傅里叶变换后实现目标距离、速度和方位的计算。基于不同的Chirp持续时间TChrip的连续调制信号，提出了一种可以消除模糊多普勒频率的估计算法。

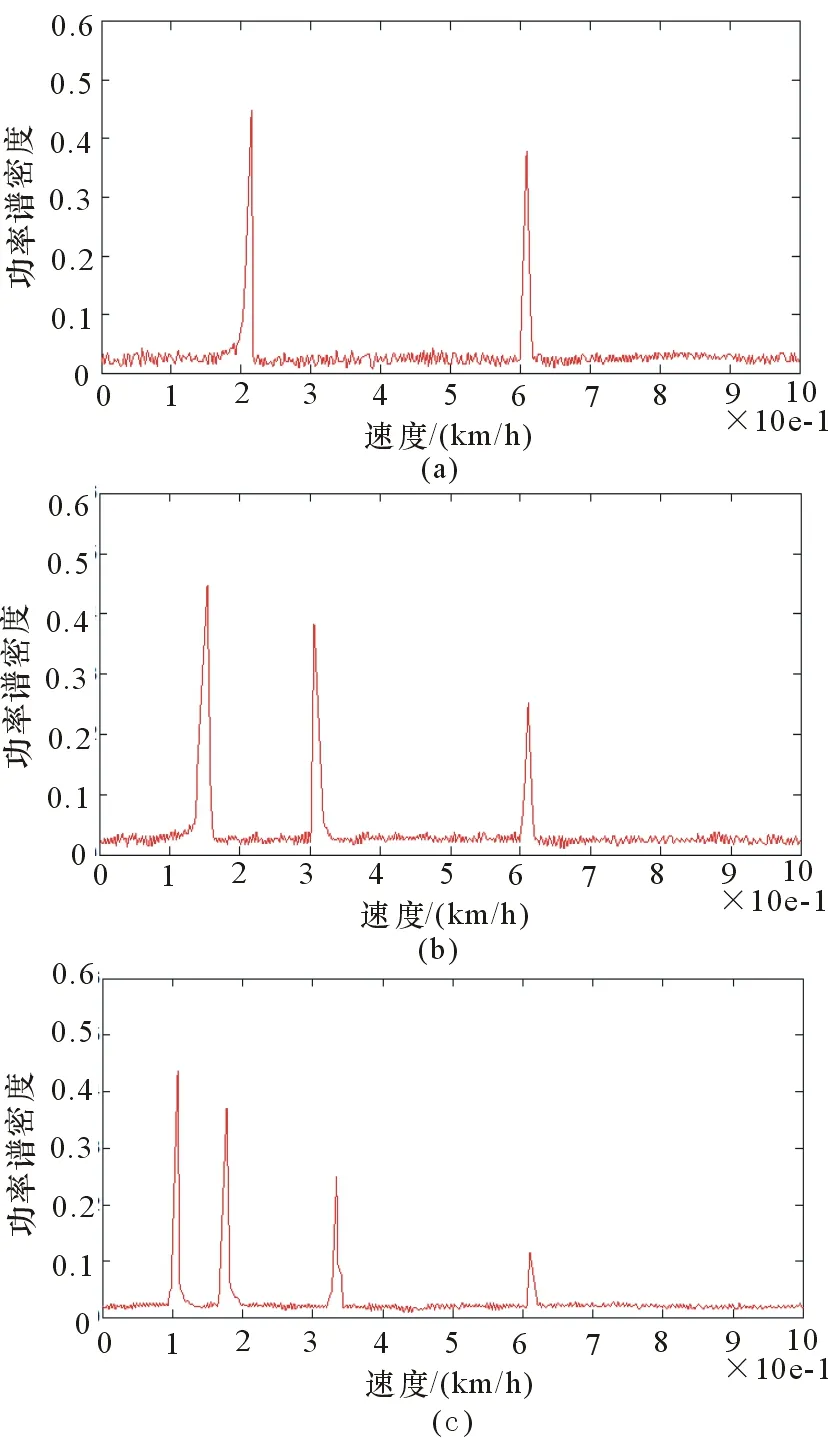
图7 3组TChirp估计的目标速度分辨单元

[1] SKOLNIK MERRILL I.Radar Handbook[M].2 edition.New York:McGraw-Hill Professional,1990.

[2] STOVE A.Linear FMCW Radar Techniques[J].Radar and Signal Processing,IEEE Proceeding,1992,139(5):343-350.

[3] BOASHASH B.Estimating and interpreting the instantaneous frequency of a signal - Part2[J].Proc.IEEE,1992,80(4):540-568.

[4] ROHLING H,MOLLER C.Radar waveform for automotive radar systems and applications[C]//2008 IEEE Radar Conference Committee.Danvers,US,2008:1-4.

[5] 王月鹏,赵国庆.二维FFT 算法在LFMCW 雷达信号处理中的应用及其性能分析[J].电子科技,2005,188(5):25-28.

A Method for Measuring Target Velocity of Millimeter-wave FMCW Radar

WAN Cheng

(The 723 Institute of CSIC,Yangzhou 225001,China)

This paper presents a continuous wave radar applied to ground monitoring that uses waveform generation of linear frequency modulation continuous wave (LFMCW) and signal processing techniques of fast fourier transform for ground moving target detection.Due to the short linear frequency modulation time and high repetition frequency,the radial velocity of the target has little influence on the intermediate frequency signal,therefore,the radial velocity is measured at each distance gate by using a number of linear frequency modulation continuous wave signals.In order to solve the maximum unambiguous radial velocity,a method changing the duration of linear frequency modulation is proposed.Finally,the target distance and azimuth angle can be calculated according to the intermediate frequency between the transmitted signals and received signals & the receiving antenna.

frequency modulation continuous wave;intermediate frequency;Doppler frequency

2016-06-22

科技成果转化项目，项目编号：YZ2015123

TN957.51

A

CN32-1413(2016)04-0047-05

10.16426/j.cnki.jcdzdk.2016.04.011