基于ITD和邻域差分能量算子解调的内燃机瞬时转速计算
刘敏, 李志宁, 张英堂, 范红波, 刘艳利
(1. 军械工程学院七系, 河北 石家庄 050003; 2. 中国北方发动机研究所(天津), 天津 300400)
基于ITD和邻域差分能量算子解调的内燃机瞬时转速计算
刘敏1, 李志宁1, 张英堂1, 范红波1, 刘艳利2
(1. 军械工程学院七系, 河北 石家庄 050003; 2. 中国北方发动机研究所(天津), 天津 300400)
针对内燃机瞬时转速计算精度低、对采样频率鲁棒性差的问题,提出了基于固有时间尺度分解(Intrinsic Time-scale Decomposition, ITD)和邻域差分能量算子解调(Energy Operator Demodulation,EOD)的瞬时转速计算方法。利用自适应波形匹配算法对原采样信号进行端点延拓,然后基于ITD算法从信号中提取包含瞬时转频的单分量信号,再对单分量信号进行邻域对称差分,并将差分结果输入传递函数计算能量算子,进而求出内燃机的瞬时转频和瞬时转速。仿真和实测信号研究证明了本方法计算速度快、精度高且频率鲁棒性好。
柴油机; 瞬时转速; 固有时间尺度分解; 能量算子解调; 邻域对称差分; 传递函数; 频率鲁棒性
内燃机瞬时转速信号测量方法简单、成本低廉、状态和故障信息丰富,易于实现在线和不解体测试,已经广泛应用于柴油机状态评估和故障诊断[1-3]。目前最常用的测量方法是基于磁电式转速传感器的脉冲测量法。采样信号的处理方法分为软件计数法和频率解调法,前者利用局部平均转速近似代替瞬时转速[4],计算精度低且对采样频率敏感,对硬件要求高;后者是从采样信号中提取瞬时转动角频率[5],进而计算得到瞬时转速,计算精度高且对采样频率不敏感,对硬件要求低,从而降低了测试成本,具有更高的研究应用价值。但是,目前瞬时转速的计算仍主要采用计数法,频率解调法的研究和应用则较少。
贾继德[5]、王明鹤[6]等对EMD和Hilbert变换在内燃机瞬时转速计算中的应用进行了研究,虽然取得了一定成果,但是Hilbert变换存在边界效应误差,而且只适用于单分量信号[7];而EMD分解虽然可以提取含有瞬时转频的单分量信号,但是存在边界效应和模态混叠,计算精度低、速度慢[8]。以上问题尚未得到有效解决,从而降低了瞬时转速频率解调法的计算精度和应用价值。
针对上述问题,本研究提出了基于ITD和EOD的柴油机瞬时转速计算方法。基于ITD算法从降噪后的采样信号中提取包含内燃机瞬时转频的单分量调频信号,并利用自适应波形匹配延拓算法消除其边界效应;然后对单分量信号进行EOD计算,求得瞬时转频信号,进而计算出瞬时转速。
1 ITD的基本原理
ITD是FREI和OSORIO在2007年提出的一种新的非线性、非平稳信号自适应时频分析方法[9]。ITD可以自适应地将任意复杂信号分解为若干具有实际物理意义的固有旋转分量(Proper Rotation Component,PRC)和一个趋势分量,与EMD或EEMD相比,具有计算精度高、分解速度快、频率分辨率高的优点,能够实时处理大量数据。所以,可以利用此算法对转速传感器输出的大量复杂多分量信号进行实时处理,将其分解为瞬时频率具有实际物理意义的一系列单分量信号,为后续处理奠定基础。
设Xt为离散信号,{τk,k=1,2,…n} 为Xt的所有局部极值点所对应的时间序列,令τ0=0 。定义L为Xt的基线提取算子,一次ITD分解表达式为
Xt=LXt+(1-L)Xt=Lt+Ht。
(1)
式中:Lt=LXt是基线分量; Ht=(1-L)Xt是固有旋转分量。
令Xk和Lk分别表示X(τk)和L(τk)。设Lt和Ht的定义域为[0,τk] , Xt的定义域为[0,τk+2] ,则在连续的极值点间隔[τk,τk+1] 内可定义Xt的分段线性基线提取因子L :

(2)
(1-a)Xk+1。
(3)
式中:a为用于控制提取固有旋转分量幅度的线性缩放, a∈[0,1],通常取0.5[10]。进而得固有旋转因子Ht为
Ht=(1-L)Xt=Xt-Lt。
(4)
重复以上过程,将原始信号分解成若干个从高到低不同频率段的固有旋转分量与一个单调趋势分量之和。分解过程可以表示为
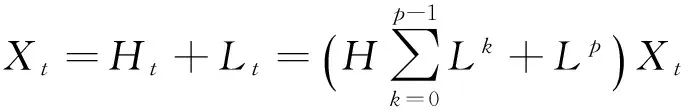
(5)
式中:HLkXt为第(k+1)层固有旋转分量;LpXt为单调趋势分量或最低频基线信号。
与EMD和EEMD类似,ITD同样存在着边界效应。本研究采用自适应波形匹配算法[10]对待处理信号进行端点延拓,以消除分解过程中的边界效应。该方法通过选取信号内部与信号端点变化趋势相同的某段子波对端点以外的信号进行延拓,从而最大限度维持信号在端点处的变化规律,使得分解结果更加真实准确。
2 EOD的基本原理
EOD是一种简单有效的调幅-调频信号解调分析方法,能够有效抑制Hilbert变换的边界效应和负频率误差,解调精度高,且算法简单,计算速度快[11-13]。理论上EOD的计算量是Hilbert变换计算量的1.25/(log2n+0.5)倍,其中n表示采样点数n∈N+[13]。所以采样点数越多 EOD的计算精度和速度优势越明显。利用该方法可以从实测单分量调频信号中快速准确地解调出内燃机的瞬时转频信号,进而求得其瞬时转速。
连续信号x(t)的能量算子定义为
Ψc[x(t)]=[x′(t)]2-x(t)x″(t)。
(6)
对于离散时间序列x(n) ,利用离散邻域对称差分代替连续微分,可得到其能量算子Ψd和Ψc之间的映射关系:

(7)
利用传递函数法求解Ψd。设系统y(n) :
y(n)=

(8)
其传递函数为
H(z)=z(1+2z-1+z-2)。
(9)
将Φd输入该系统,输出即为邻域对称差分能量算子Ψd。进而可以求得调频信号的瞬时转动角频率ω(n) :

(10)
3 仿真信号分析
磁电式转速传感器输出的电压信号的理想波形为正弦波,由于内燃机转速波动,相当于对正弦波进行幅值和频率调制。根据实测信号的调制特性,构造多分量仿真信号x(t) :

(11)
式中: x1(t)为调幅-调频信号,模拟实测信号中包含瞬时转频的单分量信号; x2(t)为正弦信号,模拟实测信号中的干扰分量。 f1=5 Hz,f2=100 Hz ,f3=10 Hz ,f4=30 Hz ,采样频率为1 000 Hz,采样时间为1 s 。
仿真信号的时域波形见图1。

图1 仿真信号波形
对x1(t)和x(t)分别进行Hilbert变换和EOD频率解调,得到瞬时频率波动曲线(见图2)。

图2 仿真信号频率解调时频谱
由图2a可以看出Hilbert变换和EOD都可以对单分量信号进行频率解调,但Hilbert存在严重的边界效应,而EOD则完全消除了此误差,解调精度更高,效果更理想。对比图2a和图2b可知,Hilbert变换与EOD均不具备多分量信号处理能力,所以必须对多分量信号进行预处理以提取有效单分量信号。
对信号x(t) 进行端点延拓后再分别进行EEMD和ITD分解,结果见图3。

图3 x(t) 的EEMD和ITD分解结果
由图3可以看出,EEMD和ITD都可以将x1(t)与x2(t)从 中分解出来,但是EEMD产生了多个虚假分量,而ITD则可以实现x1(t)与x2(t)的准确分离,不含任何干扰分量,为后续处理奠定了基础。与图1对比可知,x1(t)与x2(t)分别对应EEMD的IMF1和IMF2,以及ITD的PRC1和PRC2。以上各分量相对于原信号的分解误差见图4。
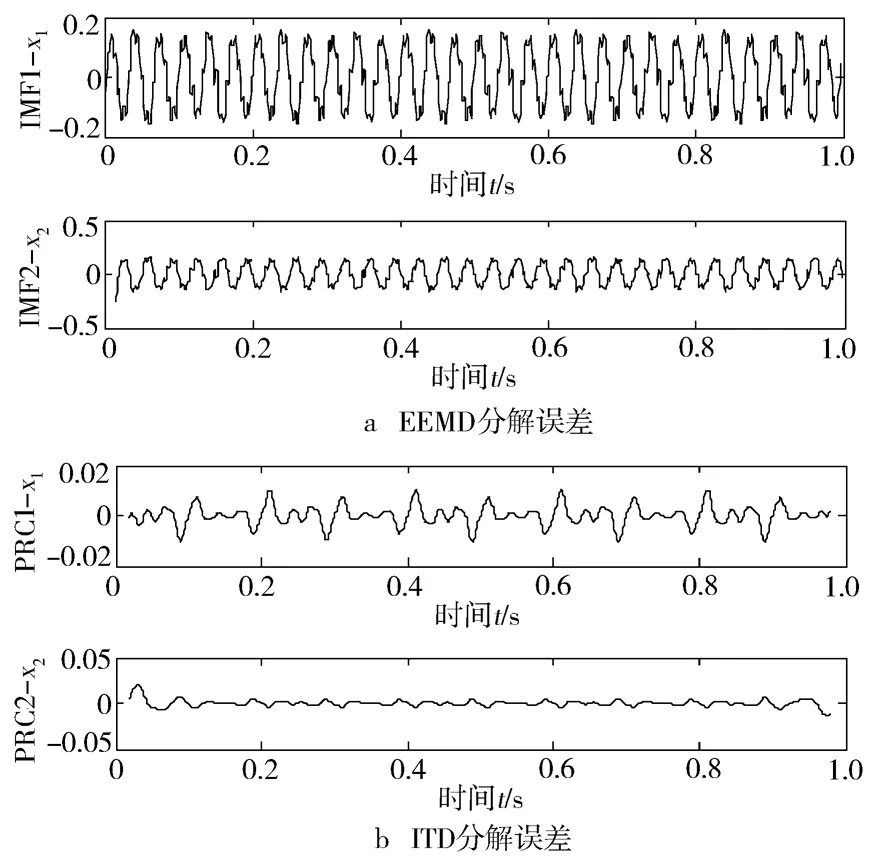
图4 EEMD和ITD分解误差
由图4可以看出,ITD对x1(t)与x2(t)的分解误差分别小于0.02和0.05,其分解精度为EEMD的10倍以上,这是由于EEMD产生了多个虚假分量,从而降低了分解精度。而且与EEMD相比,ITD算法简单,计算速度快,每次运算用时不足1 s,而EEMD每次运算用时60 s以上。
通过以上分析可知,ITD和EOD算法计算精度高、速度快。为验证本文所提ITD-EOD方法的准确性和有效性,对x(t) 分别进行EEMD-Hilbert,EEMD-EOD,ITD-Hilbert与ITD-EOD计算,得到x1(t)的瞬时频率(见图5)。


图5 频率解调时频谱
由图5可以看出ITD-EOD方法的频率解调结果最理想,所得瞬时频率波形平滑无毛刺,不存在边界效应,与原信号的瞬时频率波形基本一致。仿真分析结果证明了该方法的有效性和准确性。
4 实测信号分析
4.1 ITD和EOD算法的准确性分析
在F3L912柴油机上进行台架试验,磁电式转速传感器安装于飞轮壳,采样频率为65 536 Hz,柴油机匀速为1 200 r/min。传感器输出信号是含有干扰噪声的多分量信号。干扰噪声主要来源于飞轮齿形误差、分度误差和传感器抖动误差等。混合分量包括瞬时转速信号、机身振动信号、曲轴扭振信号及其他干扰信号[5],其中瞬时转速信号为主要成分。
由于EEMD和ITD没有自动消除噪声的能力,所以本研究采用小波降噪的方法对实测电压信号进行预处理以消除干扰噪声。降噪后信号的时域波形和时频分布见图6。从图中可以看出,实测信号是由多个频率分量组成的混合信号。

图6 电压信号
对降噪后的信号进行端点延拓,然后对其进行ITD分解,结果见图7。
由图7可知,ITD分解结果基本符合实际信号的理论组成。对比原信号幅值可知,PRC1即为包含瞬时转频的主要单分量信号。利用EOD算法计算PRC1的瞬时转动角频率,进而计算内燃机的瞬时转速,结果见图8。
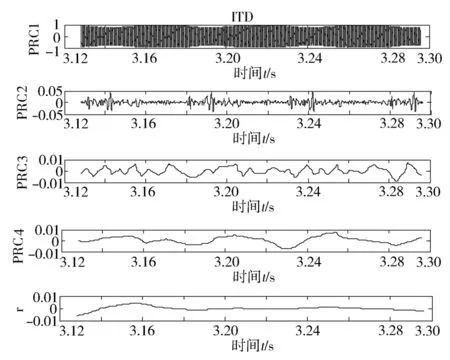
图7 实测信号分解结果

图8 内燃机瞬时转速
图8中的油压信号两峰值之间的时间段即为内燃机的一个工作循环,在此循环内瞬时转速围绕平均转速上下均匀波动3次,分别对应3个缸的发火工作过程,与试验中内燃机的实际工作过程相符。
为验证ITD-EOD方法的优越性,将其与传统的瞬时转速计算方法进行对比分析。传统方法的计算结果见图9。

图9 内燃机瞬时转速(传统方法)
对比图8和图9可知,与传统方法相比,ITD-EOD方法的瞬时转速计算结果最准确,其波形平滑,毛刺少,无边界效应和中间突变,而且计算速度快。实测信号研究结果证明了该方法的有效性和准确性。
4.2 ITD-EOD方法的频率鲁棒性分析
为分析ITD-EOD方法对采样频率的鲁棒性,对原采样信号分别以32 768 Hz和16 384 Hz进行降采样,以模拟低频采样信号。然后分别利用ITD-EOD方法和计数法计算瞬时转速,结果见图10。

图10 降采样转速
对比图10a和图10b可知,与计数法相比,ITD-EOD方法对信号的采样频率不敏感,随着采样频率的降低,瞬时转速波形基本不变,即使在极低采样频率下,仍可求得准确的瞬时转速,所以在实际测试中不需要设置高采样频率,从而降低了对测试硬件的要求,降低了测试成本;而计数法计算精度随着采样频率的降低而减小,当采样频率过低时,瞬时转速波形完全失真。实测信号研究结果证明了该方法对采样频率具有极高的鲁棒性。
5 结论
a) ITD-EOD方法有效解决了EEMD计算速度慢、虚假分量多和分解误差大的问题,同时消除了Hilbert变换的中间畸点和边界效应误差,很好地实现了单分量信号的提取和频率解调;
b) 利用ITD-EOD方法计算内燃机瞬时转速,结果表明,该方法计算速度快、精度高、对采样频率鲁棒性好,所得瞬时转速波动曲线能够很好地反映内燃机的实际工作过程,从而有效解决了现有方法速度慢、精度低、采样频率差的问题。
[1] 乔新勇,刘建敏,张小明.基于神经网络信息融合的发动机失火故障诊断[J].内燃机工程,2009,30(1):74-79.
[2] 乔国栋,徐玉秀.瞬时转速在多缸柴油机断油故障诊断中的应用[J].车用发动机,2007(5):66-69.
[3] 王维琨,江志农,张进杰.基于神经网络和瞬时转速的发动机失火故障研究[J].机电工程,2013,30(7):824-827.
[4] 林绍雄,王贵勇,申立中,等. 基于虚拟仪器的瞬时转速测试与分析[J].车用发动机,2010(6):86-88.
[5] 贾继德,孔凡让,王建平,等.基于瞬时频率估计的内燃机信号阶比分析[J].内燃机工程,2005,26(3):15-18.
[6] 王明鹤,徐金良,季晨龙,等.基于频率解调方法的柴油机瞬时转速信号计算[J].柴油机,2012,34(2):7-10.
[7] 胡异丁,任伟新,杨栋,等.基于希尔伯特变换的非平稳调幅信号解调[J].振动与冲击,2013,32(10):181-183.
[8] 段礼祥,张来斌,岳晶晶.基于ITD和模糊聚类的齿轮箱故障诊断方法[J].中国石油大学学报(自然科学版),2013,37(4):133-138.
[9] FREI M G,OSORIO I.Intrinsic time-scale decomposition: time-frequency-energy analysis and realtime filtering of non-stationary signals[J].Proceedings of the Royal Society A,2007,463:321-342.
[10] 胥永刚,陆明,付胜,等.基于匹配延拓的 ITD 边界效应抑制方法研究[J].振动与冲击,2014,33(7):165-169.
[11] Maragow P,Kaiser J F,Quatier T F.Energy Separation in Signal Modulations with Applications to Speech Analysis[J].IEEE Transactions on Signal Processing,1993,41(10):3024-3051.
[12] 曾鸣,杨宇,郑近德,等.归一化复域能量算子解调及其在转子碰摩故障诊断中的应用[J].机械工程学报,2014,50(5):65-73.
[13] 刘宝华,庞洪忠,杨凯.基于能量算子解调法的轴系扭振的测量[J].中国科技论文,2013,8(7):613-616.Calculation of Instantaneous Rotation Speed for Internal Combustion Engine Based on ITD and Neighborhood Difference Energy Operator Demodulation
[编辑: 李建新]
LIU Min1, LI Zhining1, ZHANG Yingtang1, FAN Hongbo1, LIU Yanli2
(1. Ordnance Engineering College, Seventh Department, Shijiazhuang 050003, China; 2. China North Engine Research Institude (Tianjin), Tianjin 300400, China)
In order to solve the problems of low calculation precision of instantaneous speed and poor robustness of sampling frequency, the calculation method of intrinsic time-scale decomposition(ITD) and neighborhood difference energy operator demodulation(EOD) was proposed. The end of original signal was extended with the self-adaptive waveform matching method and the single component signal containing instantaneous rotation frequency was extracted with ITD method. Neighborhood symmetric difference of the single component signal was calculated, the result of difference was used as the input of transfer function to calculate energy operator, and then the instantaneous rotation frequency and speed of internal combustion engine were calculated. The comparison of simulated and measured signal proved that the method had good speed, accuracy and frequency robustness.
diesel engine; instantaneous speed; ITD; EOD; neighborhood symmetric difference; transfer function; frequency robustness
2015-02-04;
2016-03-21
国家自然科学基金(50175109; 51305454)资助;军内科研项目
刘敏(1990—),男,硕士,主要研究方向为信息融合框架下的柴油机状态评估;hunter1848@163.com。
10.3969/j.issn.1001-2222.2016.02.002
TK428
B
1001-2222(2016)02-0007-05
——内燃机4.0 Highest Efficiency and Ultra Low Emission–Internal Combustion Engine 4.0

