基于逆建模理论的储层特征定量预测方法

刘倩, 印兴耀, 李超

1 中国石油大学(华东)地球科学与技术学院， 青岛 266580 2 中海油研究总院，北京 100028



基于逆建模理论的储层特征定量预测方法

刘倩1, 印兴耀1, 李超2

1 中国石油大学(华东)地球科学与技术学院， 青岛 266580 2 中海油研究总院，北京 100028

定量描述储层特征的物理量称为储层参数，在储层描述工作中储层参数预测是一个重要环节.本文以岩石物理理论为基础研究了利用岩石物理逆建模理论进行储层参数预测的方法.在合理、有效的岩石物理模型的基础上，逆建模方法通过弹性参数的等值面的空间交会可以预测出储层参数.在此基础上提出了一种扩展的岩石物理逆建模方法，在两个不同的储层参数域进行三维岩石物理逆建模，通过逆建模结果的参数域转换可以预测更多的储层参数，为储层特征描述提供了更加充分的数据支持.输入数据的种类对于预测结果的准确性有较大影响，利用本文建立的弹性参数适用性分析方法可以选择出适用性好的弹性参数组合作为输入数据.将本方法应用于模型数据和实际工区数据，取得了较好的预测效果，证明方法具有一定的实用性.

储层参数； 岩石物理； 逆建模； 储层参数域

1 引言

储层预测的最终目标是找到含油气储层并描述储层的物理性质.一直以来，地球物理学家们采用多种不同的思路研究如何将纵波速度、横波速度、弹性阻抗等数据转换为描述储层物理性质的数据如孔隙度、泥质含量、含水饱和度、孔隙纵横比等.Doyen(1988)基于地质统计学理论考虑空间约束条件从地震资料中预测孔隙度；Mukerji等(2001)和Eidsvik等(2004)综合岩石物理理论、统计模式识别理论和信息论提出利用统计岩石物理方法来反演储层物性参数；Avseth和Ødegaard(2004)发展了基于岩石物理模板的孔隙度和含水饱和度的估算方法；Bachrach(2006)将岩石物理随机建模方法和贝叶斯反演理论相结合，进行孔隙度和含水饱和度的联合反演；Spikes等(2007)提出了一种联合地震资料和测井数据的概率化地震反演技术实现储层参数预测；Bosch等(2010)提出一种综合马尔科夫链蒙特卡罗方法和迭代最小二乘最优化方法的地质统计学物性参数反演方法；Grana和Rossa(2010)基于贝叶斯框架和统计岩石物理建模理论提出了储层物性参数的反演方法和岩性流体分类方法；杨午阳和王丛镔(2010)利用基于模拟退火的叠前同步反演方法实现了储层物性参数的反演；胡华锋等(2012)综合统计岩石物理理论和贝叶斯分类方法提出了物性参数的联合反演方法；Jiang和Spikes(2012)基于自洽模型建立了一种搜索算法来预测页岩储层的孔隙度和孔隙纵横比；李宏兵等(2013)基于Gassmann方程和DEM解析模型利用非线性全局寻优算法来预测等效孔隙纵横比；印兴耀等(2014)建立了弹性阻抗与储层物性参数之间的线性关系，利用弹性阻抗反演方法实现了物性参数的估计；Yin等(2014)基于FFT-MA模拟方法和GDM扰动方法提出了地质统计学反演的方法来反演物性参数.

本文基于岩石物理理论建立了储层参数域，在合理、有效的岩石物理模型的基础上，在储层参数域内计算得到弹性参数的数据场和等值面，将三个不同弹性参数的单值等值面进行空间交会，就可以预测出这组弹性参数所对应的储层参数.在此基础上提出了扩展的岩石物理逆建模方法，在两个不同的三维储层参数域分别进行多次岩石物理逆建模，然后通过参数域转换及空间交会可以进行四个储层参数的预测，为储层特征定量预测提供更充分的数据支持.基于逆建模方法进行储层参数预测的优点在于对输入数据的选取较为灵活，可以根据不同工区的特点选取不同的弹性参数作为输入数据，而建立的岩石物理模型也是有针对性的，以此可以保证储层参数预测的精确程度，为储层描述提供了坚实的数据基础.

2 方法原理

在储层描述工作中，通常将纵波速度、横波速度、体积模量、剪切模量、Gassmann流体项等数据称为弹性参数；将孔隙度、泥质含量、含水饱和度、孔隙纵横比、压力等数据称为储层参数.通过建立弹性参数和储层参数之间的联系，可以从弹性参数中预测出储层参数，这有助于评价储层岩性和含油气性.

岩石物理模型是连接储层参数和弹性参数的纽带，是储层参数预测的理论基础.一个合理的岩石物理模型可以建立从储层参数到弹性参数的一一对应关系，这种对应关系是岩石物理逆建模的基础(Moyano et al.,2011).在这个基础上，逆建模方法通过在储层参数域进行等值面空间交会建立了从弹性参数到储层参数的逆向对应关系，实现了储层参数的预测.

2.1 岩石物理建模

储层参数和弹性参数之间的关系可以由下面的方程表示：

(1)

其中，m=(m1,m2,m3,…)是储层参数，如孔隙度、含水饱和度等；d=(d1,d2,d3,…)是弹性参数，如速度、模量等；F是岩石物理模型.

进行岩石物理建模的基本思想是：在假设岩石孔隙的特征尺度远远小于地震波长的前提下，将岩石孔隙等效为具有单一纵横比的理想椭球孔(Berryman,1992; Mukerji et al., 1995).按照弹性介质理论，分析岩石基质的矿物组分与体积分数，计算基质的弹性模量与密度；通过等效介质理论计算岩石骨架模量，分析储层环境下流体性质，结合流体的分布特征及其与孔隙结构的联系，估算含流体岩石的弹性模量.

岩石物理逆建模过程不依赖特定的岩石物理模型，大多数岩石物理模型都可以根据逆建模理论建立相应的逆建模方法.在实际应用过程中要根据具体的储层特点建立合适、准确的模型，使得模型能够准确描述储层的岩石物理特点，并保证利用模型重构得到的弹性参数曲线与实际测井结果一致.本文以下面的岩石物理建模过程为例，进行逆建模方法的说明.具体的储层岩石物理模型的构建步骤如下：

首先利用Voigt-Reuss-Hill平均理论(Hill，1952)计算岩石基质的等效弹性模量MVRH：

(2)

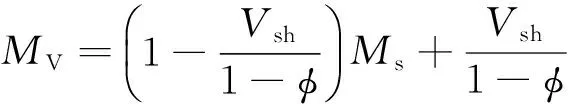
然后利用微分等效介质模型(DEM模型)在基质中添加孔隙，计算岩石骨架的弹性模量，等效模量K*和μ*的耦合微分方程分别是

(3)

初始条件是K*(0)=K1，μ*(0)=μ1，其中K1、μ1是利用方程(2)计算得到的基质的体积模量和剪切模量；K2、μ2是逐渐加入的包含物的体积模量和剪切模量，y是包含物的含量，P(*2)和Q(*2)是背景介质中包含物形状的表达式.

最后利用Gassmann方程在岩石孔隙中充填流体(Gassmann，1951)，饱和岩石弹性模量的表达式如下：

(4)

其中，Ksat和μsat是饱和岩石弹性模量，K*和μ*是干岩石骨架弹性模量；Kf是混合流体的体积模量，使用Wood公式计算得到.

密度的计算方程为

ρ= φ((1-Sw)ρh+Swρw)

+(1-φ)(VshρC+(1-Vsh)ρQ)，

(5)

其中，ρh、ρw、ρC和ρQ分别是油(气)、水、粘土和石英的密度.

根据前述的岩石物理建模方法，结合表1中的参数，可以建立弹性参数随储层参数的变化关系，如图1所示.图1a—1d分别是岩石体积模量和剪切模量随孔隙度、泥质含量、含水饱和度和孔隙纵横比的变化图.从图中可以看出，当其他储层参数一定的时候，随着泥质含量的增加，体积模量和剪切模量都减小；随着含水饱和度的增加，体积模量增加，剪切模量不受影响；随着孔隙度的增加，体积模量和剪切模量都减小；随着孔隙纵横比的增加，体积模量和剪切模量都增加.岩石物理模型建立了弹性参数与储层参数之间的联系，不同的岩石物理模型建立的联系不尽相同，根据这些关系进行的逆建模结果也不同，因此建立准确、合理的岩石物理模型至关重要.

表1 基本组分参数表Table 1 Basic constituent parameters table

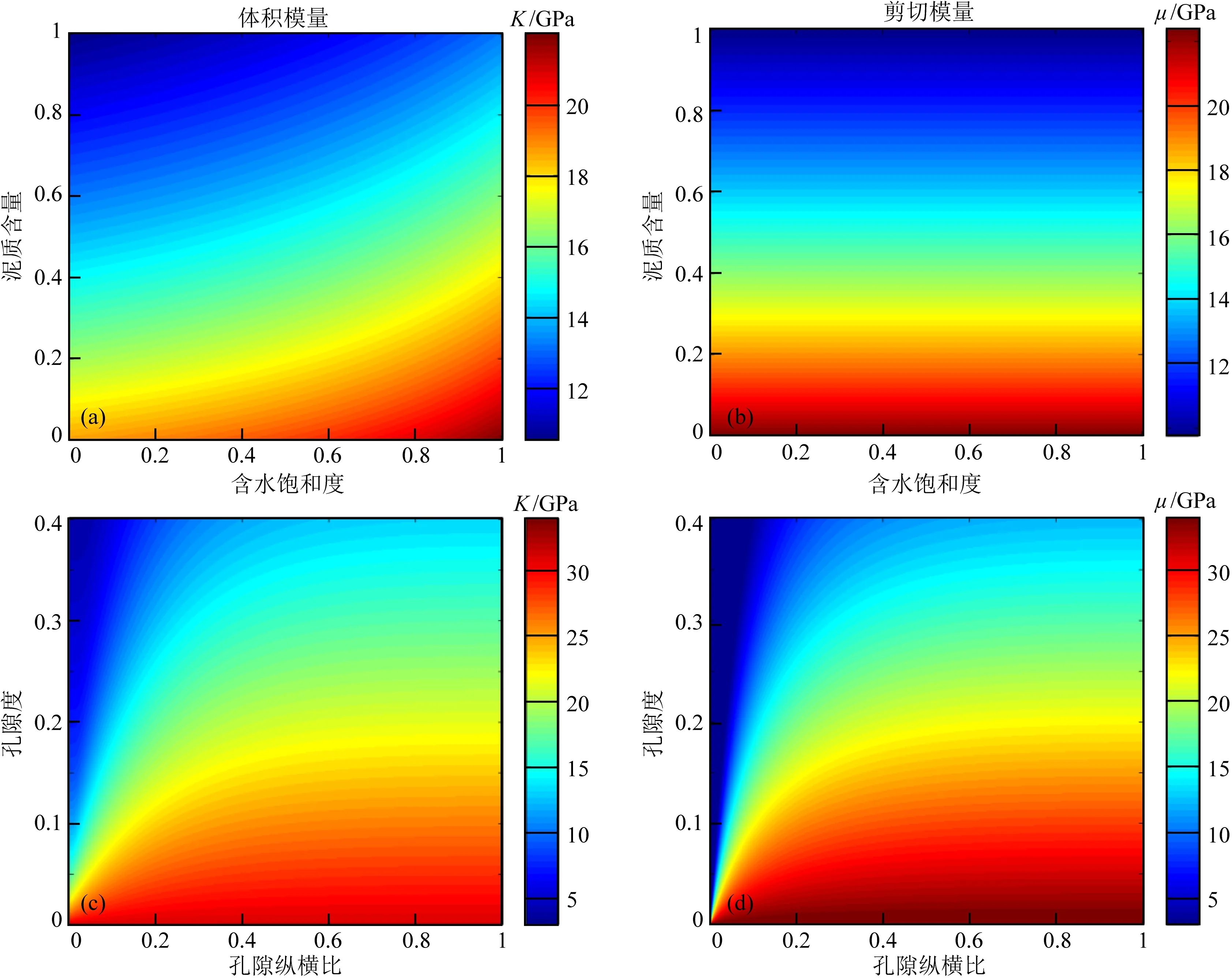
图1 弹性参数随储层参数变化图(a) 体积模量随泥质含量和含水饱和度的变化； (b) 剪切模量随泥质含量和含水饱和度的变化； (c) 体积模量随孔隙度和孔隙纵横比的变化； (d) 剪切模量随孔隙度和孔隙纵横比的变化.Fig.1 The variation of elastic parameters with reservoir parameters(a) The variation of bulk modulus with clay content and water saturation; (b) The variation of shear modulus with clay content and water saturation; (c) The variation of bulk modulus with porosity and aspect ratio; (d) The variation of shear modulus with porosity and aspect ratio.

2.2 岩石物理逆建模

由岩石物理建模过程可以看出，岩石物理模型表示的岩石弹性参数与储层参数之间的关系是强非线性的，要推导其逆运算的解析表达式、直接计算出储层参数是很困难的，因此需要利用逆建模方法间接地完成预测.

2.2.1 三维岩石物理逆建模

岩石物理逆建模是在储层参数域中，根据岩石物理模型建立弹性参数的单值等值面，通过等值面的空间交会得到交点坐标，完成储层参数的预测.在三维储层参数域，需要三个单值等值面的交会才能得到一个稳定的交点.三维岩石物理逆建模的具体步骤如下：

以一组实测弹性参数d0(K0,μ0,ρ0,f0,M0)作为逆建模的输入数据，要保证反问题是非欠定的，需要至少有三种输入数据，这里选取的是体积模量K0、Gassmann流体项f0和密度ρ0(Russell et al.，2003).

选取孔隙度φ、含水饱和度Sw和等效孔隙纵横比α建立一个三维直角坐标系，称为一个储层参数域.分别以φ,α,Sw为x轴、y轴和z轴，取值范围分别是(0～0.4)，(0.001～1)和(0～1)，各坐标轴均匀采样.则方程(1)可以表示为

(6)

∀φ∈(φmin,φmax),Sw∈(Swmin,Swmax),α∈(αmin,αmax)其中，φmin,φmax、Swmin,Swmax和αmin,αmax分别是孔隙度、含水饱和度和等效孔隙纵横比的最小值和最大值.

储层参数域中每个点的坐标是一组储层参数值，利用建立的岩石物理模型计算出每一个点对应的弹性参数值，可得到一个三维的数据场.图2是体积模量的三维数据场，这个数据场中包含所有可能的体积模量值.根据相同的原理可以建立Gassmann流体项和密度的三维数据场.

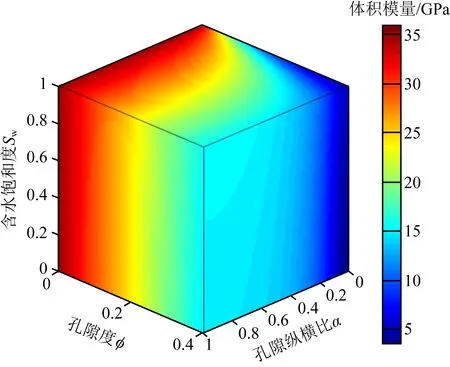
图2 储层参数域的体积模量数据场Fig.2 The bulk modulus data cube in the reservoir parameter domain

这里采用Marching Cubes算法求取数据场中的单值等值面(Lorensen and Cline，1987).算法的主要思想是将三维数据场划分为多个小的立方体，作为最小搜索单元(称为体元).逐个处理数据场的体元，选出与等值面交会的体元，采用线性插值计算出与等值面交会的体元的棱边上的交点，根据体元8个顶点与等值面的相对位置，将这些交点连接成体元内的等值面，所有体元中的等值面构成整个数据场的等值面.在等值面的空间结构比较简单的情况下，经典的Marching Cubes算法就可以完成；在等值面的空间构型较为复杂情况下，需要使用改进的Marching Cubes算法(梁秀霞等，2006)，以保证曲面拟合的精度和效率.

利用Marching Cubes算法计算体积模量为K0的单值等值面(这里用ISK0(φ,Sw,α)来表示)，如图3a所示.等值面在坐标轴的投影宽度代表该弹性参数对该储层参数的约束能力，投影越窄约束能力越强，预测得到的储层参数越准确.同理可以得到密度为ρ0在储层参数域的等值面(用ISρ0(φ,Sw,α)来表示)，如图3b所示.将体积模量的单值等值面和密度的单值等值面交会在同一个储层参数域中，即可找到体积模量和密度值均与实测值相等的点.如图4a所示，这些点就分布在两个等值面的交线上，可以通过求解方程ISK0(φ,Sw,α)=ISρ0(φ,Sw,α)获取交点坐标.利用模拟退火算法求取交线上的点坐标，只需建立如方程(7)的目标函数，在两个单值等值面的定义域交集内求取目标函数的最小值即可.

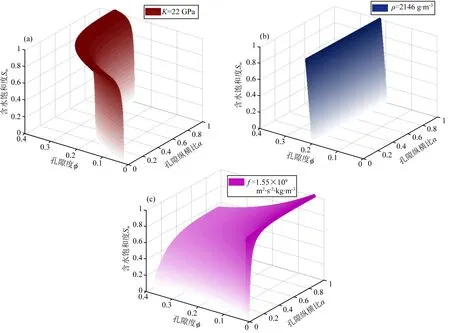
图3 储层参数域的单值等值面(a) 体积模量； (b) 密度； (c) Gassmann流体项.Fig.3 Single isosurfaces in the reservoir parameter domain(a) Bulk modulus； (b) Density； (c) Gassmann fluid term.

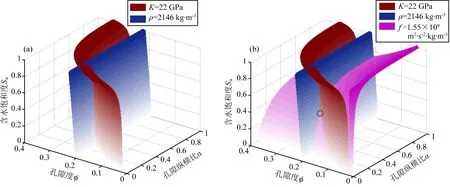
图4 不同单值等值面的交会(a) 两个等值面的交会； (b) 三个等值面的交会.Fig.4 Intersections of different isosurfaces(a) 2 isosurfaces；(b) 3 isosurfaces.

J1=(φK0-φρ0)2+(SwK0-Swρ0)2+(αK0-αρ0)2，

(7)

其中，φK0,SwK0,αK0,φρ0,Swρ0,αρ0是单值等值面ISK0(φ,Sw,α)中点的坐标和单值等值面ISρ0(φ,Sw,α)中点的坐标.

计算出Gassmann流体项为f0在储层参数域的单值等值面(用ISf0(φ,Sw,α)来表示)，如图3c所示.将其与图4a中的两个单值等值面交会在一起，结果如图4b所示，三个等值面的交集部分是图中黑色圆圈标出的点，这个点的体积模量、Gassmann流体项和密度的值均与实测值(K0,f0,ρ0)相等，它的坐标即所求储层参数，可以通过求解方程ISK0(φ,Sw,α)=ISf0(φ,Sw,α)=ISρ0(φ,Sw,α)获取交点坐标.利用模拟退火算法求取交点坐标，只需建立如方程(8)的目标函数，在三个单值等值面的定义域交集内求取目标函数的最小值即可，得到的最终解是(φ=0.19,Sw=0.49,α=0.30).

J2=(φK0-φρ0)2+(SwK0-Swρ0)2+(αK0-αρ0)2

+(φK0-φf0)2+(SwK0-Swf0)2+(αK0-αf0)2,

(8)

其中，φf0,Swf0,αf0是等值面ISf0(φ,Sw,α)中的点的坐标.

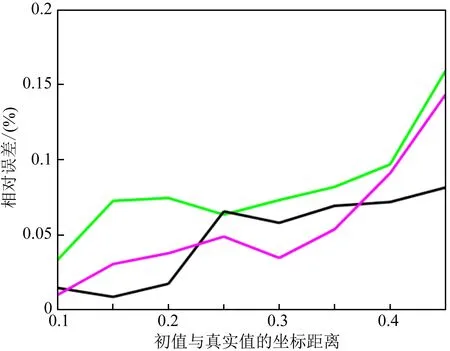
图5 不同初值情况下得到的解的相对误差Fig.5 Relative errors under conditions of different initial values

这里使用的模拟退火算法是非常快速模拟退火算法(Ingber，1989；陈华根等，2004)，通过不断的试验，调整算法的参数，使之达到最优，不仅有较高的运算效率，而且不易陷入局部极小值.为了研究初始值对于本方法的影响，以d0(K0,f0,ρ0)输入数据，选取了一系列不同的初始值用于三维岩石物理逆建模中的模拟退火运算，进行10000次模拟退火运算得到的结果取平均值，在10000次模拟结果中均未出现局部极值的情况.图5是计算结果的相对误差随初始值的变化关系，图中的横轴是这些点与真实值所在坐标的距离，距离越小说明初始值与真实值更接近，纵轴是估计得到的储层参数的相对误差，其中黑色线、粉色线和绿色线分别表示孔隙度、孔隙纵横比和含水饱和度的相对误差.从图中可以看出，初始值越接近真实值，误差越小，因此在实际应用中使用的初始值应该尽量准确，这不仅有助于提高准确性，还可以减少迭代次数，提高收敛的效率.在井位置处可以利用测井得到的储层参数曲线经过平滑处理后的结果作为初始值，在井旁道位置处可以利用测井得到的储层参数曲线进行插值外推的结果作为初始值.

2.2.2 扩展的岩石物理逆建模

为了给储层特征描述工作提供更多的数据，基于岩石物理逆建模理论可以进行四个储层参数的预测.四个参数的预测对于前述的岩石物理逆建模方法来说是一种欠定的反问题，无法得到唯一解，因此建立扩展的岩石物理逆建模方法：选择要预测的四个储层参数：泥质含量Vsh、孔隙度φ、含水饱和度Sw和等效孔隙纵横比α，可以建立四个不同的三维参数域(φ,Sw,α)、(φ,Vsh,α)、(φ,Sw,Vsh)和(Vsh,Sw,α)，在其中选择两个参数域(φ,Sw,α)和(φ,Vsh,α)；Vsh和Sw在各自的定义域内均匀取值，针对每个Vsh的不同取值在参数域(φ,Sw,α)内、针对每个Sw的不同取值在参数域(φ,Vsh,α)内分别进行三维岩石物理逆建模，将两组逆建模结果综合交会进行预测.

这样通过逆建模得到了n个不同泥质含量情况下的交点.将m1(φ,Sw,α,Vsh)投影到储层参数域(φ,Sw,α)中，通过插值得到曲线m1(φ,Sw,α)，投影方程表示为

m1(φ,Sw,α,Vsh)T=m1(φ,Sw,α)，

(9)

其中，T是4×3的投影矩阵，由于坐标轴Vsh与参数域(φ,Sw,α)是正交的，因此投影矩阵中的元素t11=t22=t33=1，其他元素都为0；m1(φ,Sw,α)表示m1(φ,Sw,α,Vsh)投影以后的曲线，这条线包含最终的解.

(10)

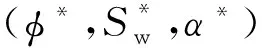
(11)

其中，φm1,φm2,Swm1,Swm2,αm1,αm2分别表示曲线m1(φ,Sw,α)和m2(φ,Sw,α)上的点坐标.

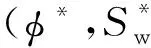
图6 不同泥质含量情况下的体积模量数据场示意图Fig.6 Data cubes of bulk modulus with different clay contents

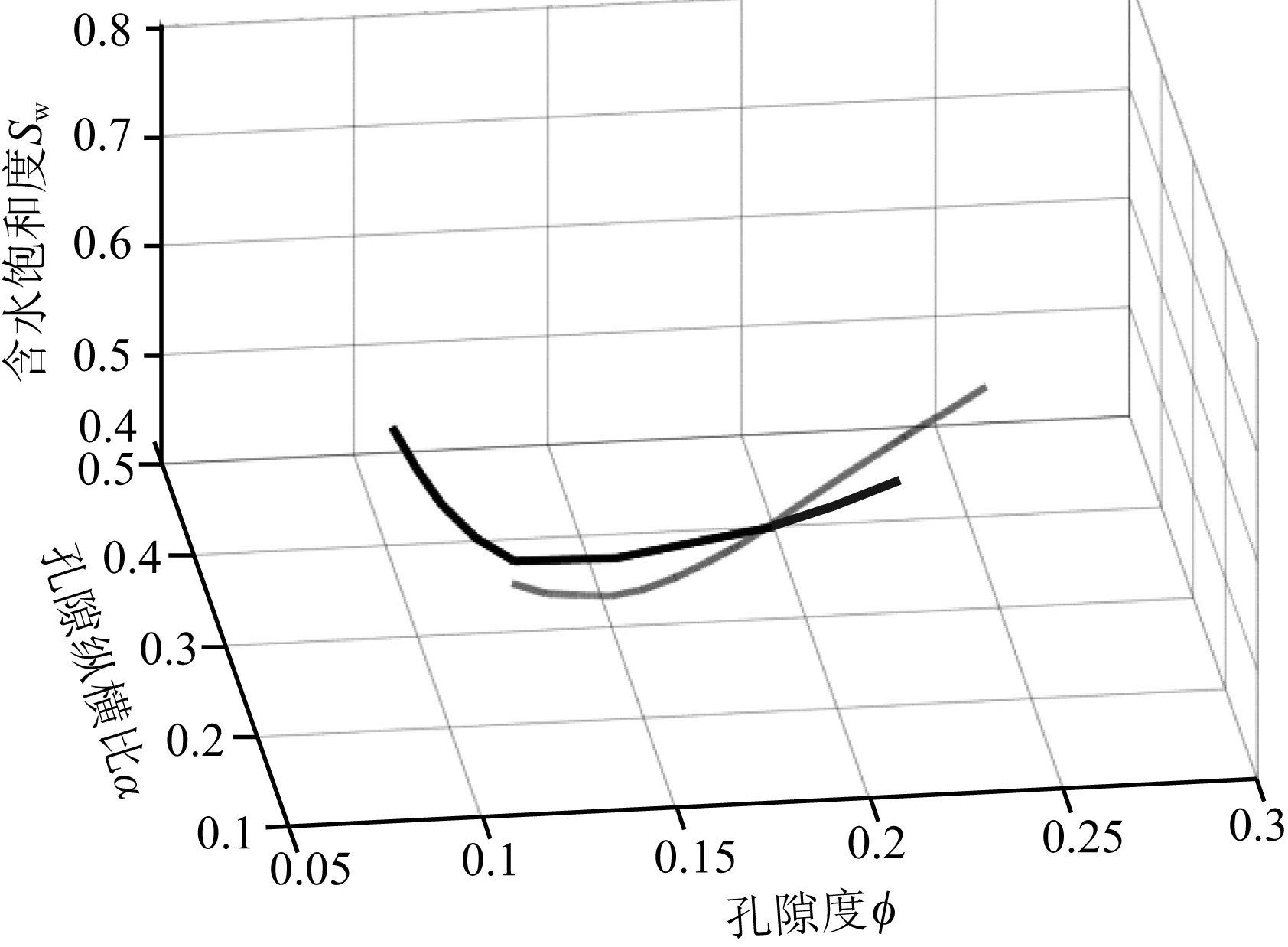
图7 两个储层参数域的逆建模结果的投影的交会图Fig.7 Intersection of projections of inverse modeling results from two reservoir parameter domains

2.3 输入数据的适用性分析

可以用于岩石物理逆建模的弹性参数有许多，在进行储层参数预测时，选取合适的弹性参数是预测成功的关键步骤之一.对弹性参数数据的选取主要取决于在建立的岩石物理模型框架下参数的单值等值面的形状，相互平行的单值等值面没有交线，不平行的单值等值面容易得到交线，越趋于正交的单值等值面越有利于获得准确的最终解.两个单值等值面之间的正交性可以表示为

(12)

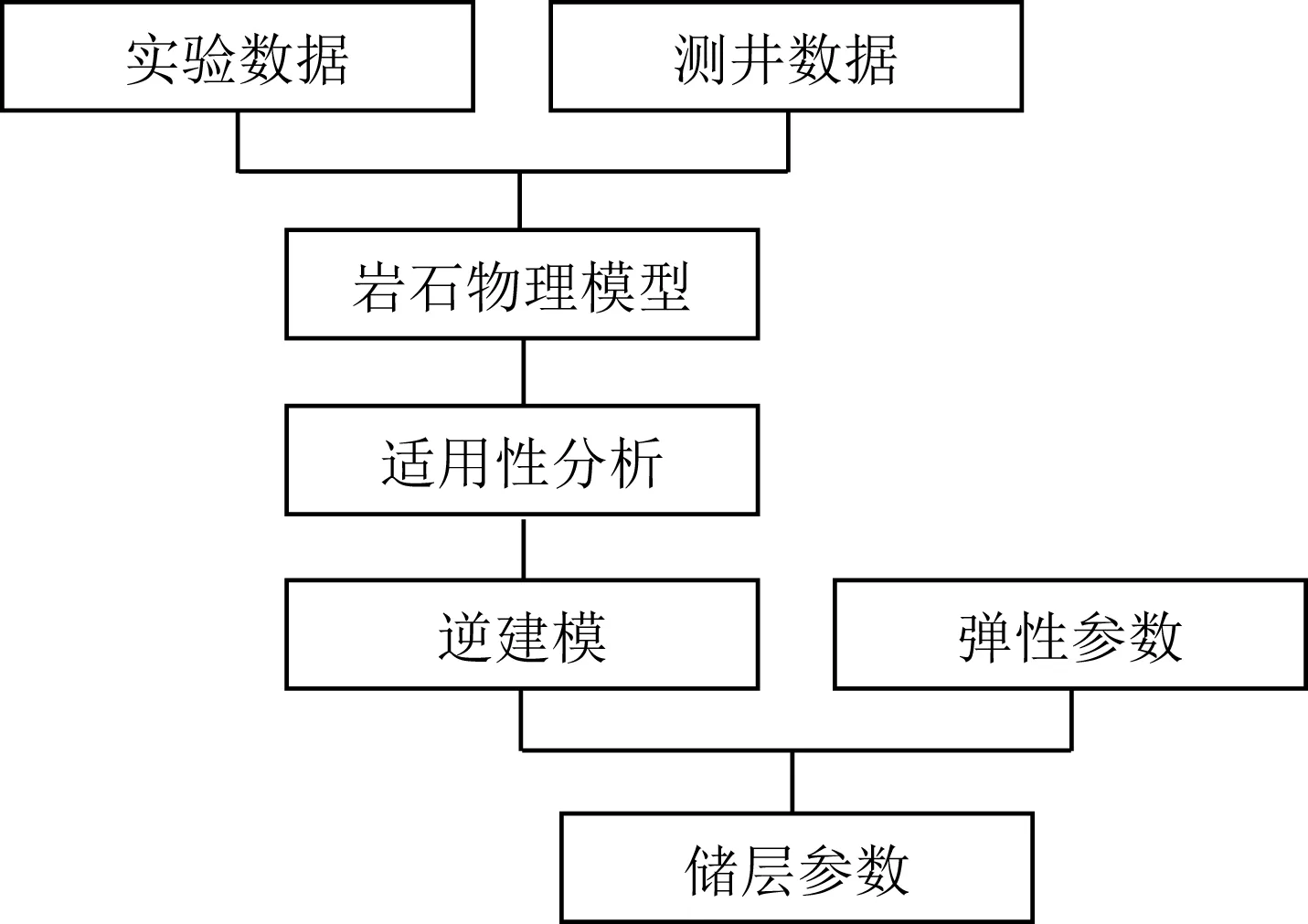
图8 储层参数预测流程图Fig.8 Flowchart of reservoir parameter prediction

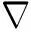
建立如下的适用性因子来衡量一组弹性参数的适用性：

(13)

其中，TOF是一组弹性参数的适用性因子，OFdidj是弹性参数组中任意两种不同弹性参数的正交性因子，i=1,2,…n，j=1,2,…n，i≠j，N是正交性因子的个数.

方程(13)是一个参数组中各参数等值面之间的正交性因子的均值，若TOF趋近于1，则这个参数组中的各弹性参数的等值面之间的正交性差，易产生多个解；若TOF趋近于0，则各弹性参数的等值面之间的正交性强，易找到唯一解.

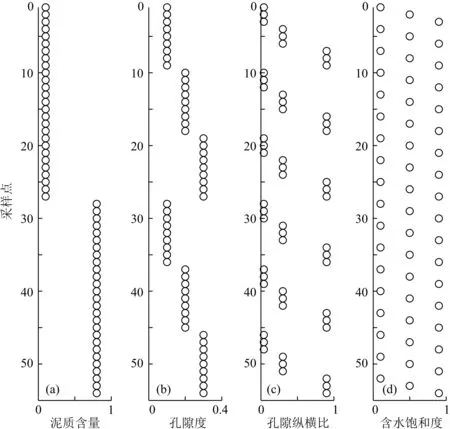
图9 原始模型(a) 泥质含量； (b) 孔隙度； (c) 等效孔隙纵横比； (d) 含水饱和度.Fig.9 Original model(a) Clay content； (b) Porosity； (c) Effective pore aspect ratio； (d) Water saturation.

利用方程(13)计算弹性参数组的适用性因子，可以在进行岩石物理逆建模之前就了解各组参数的适用性.整个基于逆建模的储层参数预测流程如图8所示.

3 模型试算

为了检验基于逆建模的储层特征定量预测方法的有效性，建立如图9所示的模型，其中有54个点，对应的泥质含量、孔隙度、含水饱和度和等效孔隙纵横比分别如图9a—9d所示.然后根据前述的岩石物理建模方法可以计算出多个弹性参数曲线.为了找到合理的弹性参数，首先根据方程(13)计算不同参数组合的适用性，分别计算模型中每个点的适用性因子，然后取平均值，得到的结果如图10所示.图10中横坐标1到5分别表示M/μ,K,ρ,f、M/μ,Vp,ρ,μ、K,f,μ,Vp/Vs、Ip,Is,K,μ和Vp,Vs,ρ,K这些参数的组合，纵坐标为适用性因子的值.

通过比较可以看出，体积模量K、Gassmann流体项f、密度ρ和模量比M/μ是适用性较强的组合，因此可以利用这些弹性参数进行储层参数预测，其曲线如图11所示.利用这四个参数进行扩展的岩石物理逆建模，得到的预测结果如图12所示.图12中空心点是图9中的原始模型数据，实心点是预测出的储层参数值，从图中可以看出，四个储层参数的值都较为准确，相比而言含水饱和度和等效孔隙纵横比的精度略差.

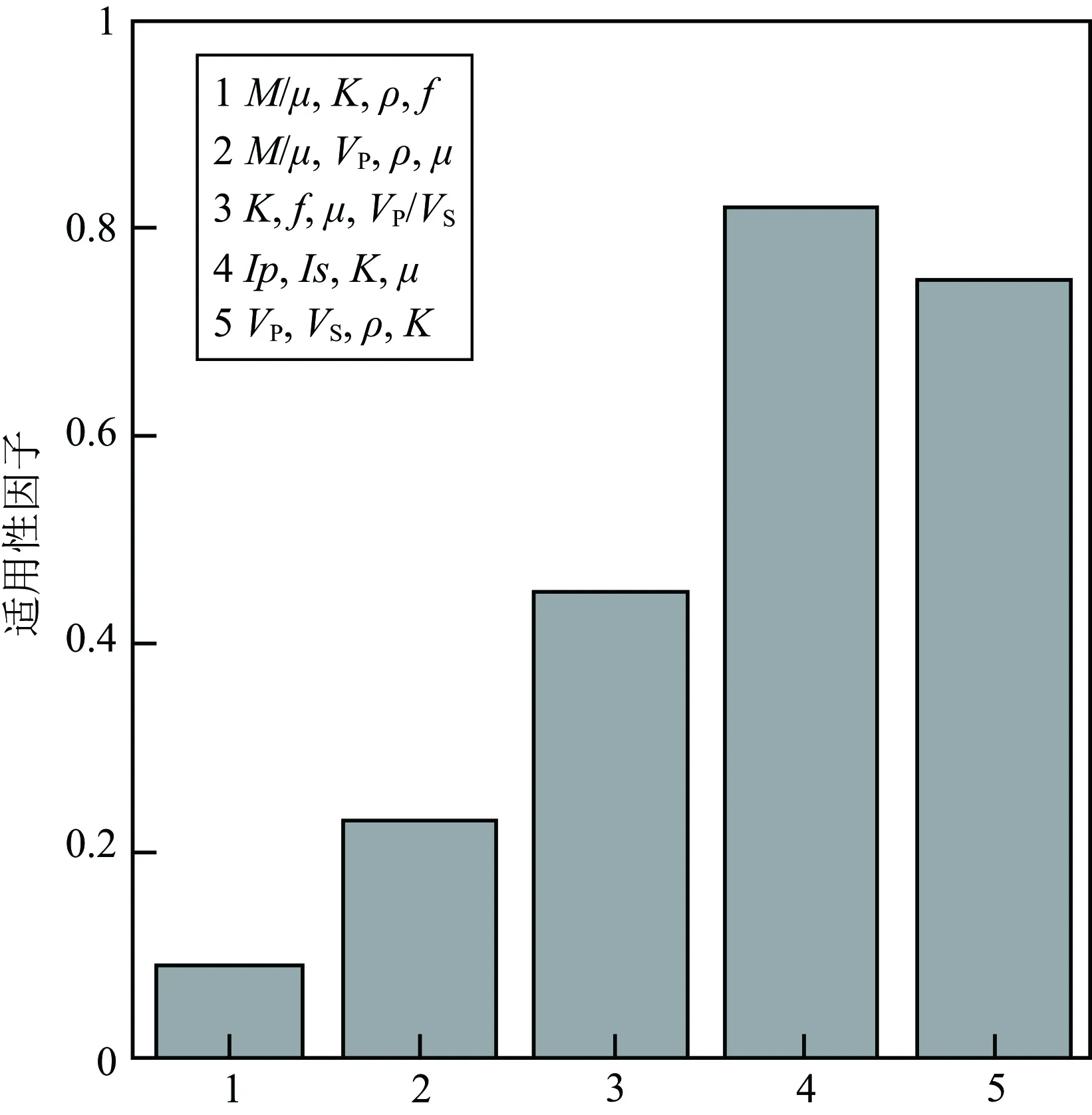
图10 弹性参数组合的适用性对比Fig.10 Comparison of applicability of different combinations of elastic parameters

图11 弹性参数曲线(a) 体积模量； (b) Gassmann流体项； (c) 密度； (d) 模量比.Fig.11 Logs of elastic parameters(a) Bulk modulus； (b) Gassmann fluid term； (c) Density； (d) Moduli ratio.

图12 预测结果与原始模型的对比(a) 泥质含量； (b) 孔隙度； (c) 等效孔隙纵横比； (d) 含水饱和度.Fig.12 Comparison of predictions and original data(a) Clay content； (b) Porosity； (c) Effective pore aspect ratio； (d) Water saturation.

4 实际应用

将本文所述方法应用于中国东部某油田的实际资料.综合工区的测井、录井、地质和实验数据，建立合理的岩石物理模型，并选取合适的基础参数.首先利用该工区的一口井(A井)的数据进行扩展的岩石物理逆建模，结果如图13所示.图13中从左到右依次是泥质含量、孔隙度、含水饱和度和等效孔隙纵横比，其中实线是测井数据，虚线是预测结果.通过对比可以看出，预测结果较为准确.

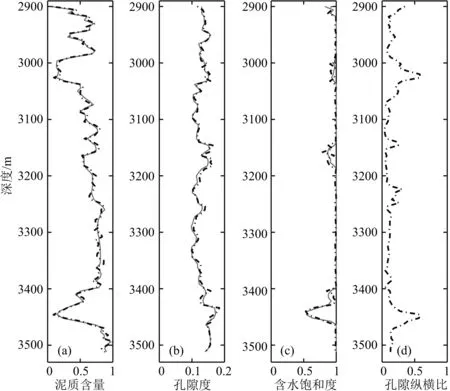
图13 利用井数据的预测结果与实际测量数据的对比Fig.13 Comparison of predictions from well data and the measured data

接下来进行地震反演和基于地震反演结果的扩展的岩石物理逆建模.图14是过工区中A井的地震剖面，进行叠前地震反演之前，需要对地震数据进行保幅处理.通过弹性参数组的适用性分析发现体积模量、Gassmann流体项、密度和模量比M/μ是适用性较好的参数组合，可以作为输入数据.

随后利用叠前反演得到以上四种弹性参数，并进行扩展的岩石物理逆建模，储层参数预测结果如图15所示.图15a—15d分别是预测得到的泥质含量、孔隙度、含水饱和度和等效孔隙纵横比剖面，在图15a—15c中井位置处的黑色井曲线分别是对应的实际测井曲线.从图15中看出，2.4 s、2.5 s和2.65 s深度处有三层砂岩，分别称其为第一层、第二层和第三层砂岩.其中，第一层和第三层砂岩的泥质含量较低、等效孔隙纵横比较高，是较好的砂岩储层，而第二层砂岩虽然孔隙度高，但是泥质含量偏高，不是好的砂岩储层.第一层和第二层的含水饱和度值偏高，不是含油气储层，第三层的含水饱和值较低，发育的是有利储层.实际测井解释结果和钻井结果显示，这三个位置钻遇砂岩，第一层和第二层是含水砂岩层，第三层是含油砂岩层.通过比较可以看到，预测结果和实际数据匹配较好，证明方法具有一定的实用性.

图14 过A井的地震剖面Fig.14 Seismic profile across well A

5 结论

储层参数是我们理解岩石的几何特性和动力学特性的必备要素，也是油气勘探中评价储层的重要依据，因此进行储层参数预测具有重要意义.本文基于岩石物理理论研究了三维岩石物理逆建模方法，通过在储层参数域建立弹性参数的单值等值面并进行等值面的空间交会，完成了储层参数的预测.在此基础上，提出了扩展的岩石物理逆建模方法预测四个储层参数.岩石物理逆建模是一种灵活性很强的方法，使用的岩石物理模型和输入参数都不是固定的，可以根据具体的目标储层特征有针对性地选择，这样有利于提高预测结果的精确程度.经过模型数据的检验和实际工区的应用，本方法取得了不错的应用效果，说明了方法具有一定的实用性.

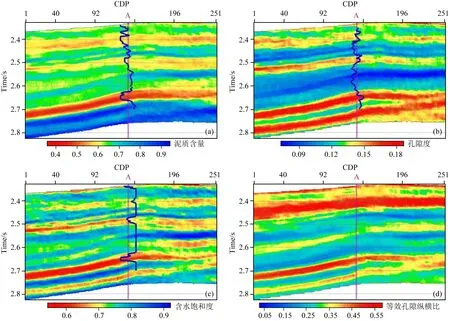
图15 储层参数预测结果剖面(a) 泥质含量； (b) 孔隙度； (c) 含水饱和度； (d) 等效孔隙纵横比.Fig.15 Profiles of predicted reservoir parameters(a) Clay content； (b) Porosity； (c) Water saturation； (d) Effective pore aspect ratio.

该方法的前提是有合理的岩石物理模型，因此在实际应用中岩石物理模型的建立至关重要，模型和参数的选择要尽可能的准确、合理.为了提高预测的效率和结果的精度，建立了弹性参数组适用性评价方法，这种方法可以在储层参数预测之前就优选出适用性强的参数组合.类似地，在其他类型的储层的描述中也可以建立类似的储层参数预测方法.

Avseth P A, ∅degaard E. 2004. Well log and seismic data analysis using rock physics templates.FirstBreak, 22(10): 37-43.

Bachrach R. 2006. Joint estimation of porosity and saturation using stochastic rock-physics modeling.Geophysics, 71(5): O53- O63. Berryman J G. 1992. Single-scattering approximations for coefficients in Biot′s equations of poroelasticity.TheJournaloftheAcousticalSocietyofAmerica, 91(2): 551-571. Bosch M, Mukerji T, Gonzalez E F. 2010. Seismic inversion for reservoir properties combining statistical rock physics and geostatistics: A review.Geophysics, 75(5): 75A165-75A176.

Chen H G, Wu J S, Wang J L, et al. 2004. Mechanism study of simulated annealing algorithm.JournalofTongjiUniversity(NaturalScience), 32(6): 802-805.

Doyen P M. 1988. Porosity from seismic data: A geostatistical approach.Geophysics, 53(10): 1263-1275.

Eidsvik J, Avseth P, More H, et al. 2004. Stochastic reservoir characterization using prestack seismic data.Geophysics, 69(4): 978-993. Gassmann F. 1951. Uber die elastizitat, poroser medien. Vierteljahrsschrift der NaturforschendenGesellschaftinZurich, 96: 1-23.Grana D, Rossa E D. 2010. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion.Geophysics, 75(3): O21-O37.

Hill R. 1952. The elastic behaviour of a crystalline aggregate. Proceeding of the Physical Society.SectionA, 65(5): 349-354.

Hu H F, Yin X Y, Wu G C. 2012. Joint inversion of petrophysical parameters based on Bayesian classification.GeophysicalProspectingforPetroleum(in Chinese), 51(3): 225-232.

Ingber L. 1989. Very fast simulated re-annealing.MathematicalandComputerModelling, 12(8): 967-973. Jiang M J, Spikes K. 2012. Estimation of the porosity and pore aspect ratio of the Haynesville Shale using the Self-Consistent Model and a Grid Search Method. ∥ 82th Annual International Meeting, Society of Exploration Geophysicists. Expanded Abstracts, 1-5. Li H B, Zhang J J, Yao F C. 2013. Inversion of effective pore aspect ratios for porous rocks and its applications.ChineseJ.Geophys. (in Chinese), 56(2): 608-615, doi: 10.6038/cjg20130224.

Liang X X, Zhang C M, Liu Y, et al. 2006. A topology complexity based method to approximate isosurface with trilinear interpolated triangular patch.JournalofComputerResearchandDevelopment(in Chinese), 43(3): 528-535. Lorensen W E, Cline H E. 1987. Marching cubes: a high resolution 3D surface construction algorithm.ACMSIGGRAPHComputerGraphics, 21(4): 163-169. Moyano B, Jensen E H, Johansen T A. Improved quantitative calibration of rock physics models.PetroleumGeoscience, 2011, 17(4): 345-354.Mukerji T, Berryman J, Mavko G, et al. 1995. Differential effective medium modeling of rock elastic moduli with critical porosity constraints.GeophysicalResearchLetters, 22(5): 555-558.Mukerji T, Avseth P, Mavko G, et al. 2001. Statistical rock physics: Combining rock physics, information theory, and geostatistics to reduce uncertainty in seismic reservoir characterization.TheLeadingEdge, 20(3): 313-319.

Russell B H, Hedlin K, Hilterman F J, et al. 2003. Fluid-property discrimination with AVO: A Biot-Gassmann perspective.Geophysics, 68(1): 29-39. Spikes K, Mukerji T, Dvorkin J, et al. 2007. Probabilistic seismic inversion based on rock-physics models.Geophysics, 72(5): R87-R97.

Yang W Y, Wang C B. 2010. Utilizing pre-stack simultaneous inversion to predict reservoir physical properties.OilGeophysicalProspecting(in Chinese), 45(3): 414-417.Yin X Y, Cui W, Zong Z Y, et al. 2014. Petrophysical property inversion of reservoirs based on elastic impedance.ChineseJ.Geophys. (in Chinese), 57(12): 4132-4140, doi: 10.6038/cjg20141224.

Yin X Y, Sun R Y, Wang B L, et al. 2014. Simultaneous inversion of petrophysical parameters based on geostatistical a priori information.AppliedGeophysics, 11(3): 311-320.

附中文参考文献

陈华根, 吴健生, 王家林等. 2004. 模拟退火算法机理研究. 同济大学学报(自然科学版), 32(6): 802-805.

胡华锋, 印兴耀, 吴国忱. 2012. 基于贝叶斯分类的储层物性参数联合反演方法. 石油物探, 51(3): 225-232.

李宏兵, 张佳佳, 姚逢昌. 2013. 岩石的等效孔隙纵横比反演及其应用. 地球物理学报, 56(2): 608-615, doi: 10.6038/cjg20130224. 梁秀霞, 张彩明, 刘毅等. 2006. 拓扑结构正确的三线性插值曲面的三角片逼近. 计算机研究与发展, 43(3): 528-535.

杨午阳, 王丛镔. 2010. 利用叠前AVA同步反演预测储层物性参数. 石油地球物理勘探, 45(3): 414-417.

印兴耀, 崔维, 宗兆云等. 2014. 基于弹性阻抗的储层物性参数预测方法. 地球物理学报, 57(12): 4132-4140, doi: 10.6038/cjg20141224.

(本文编辑 胡素芳)

Quantitative prediction of reservoir characteristics based on inverse modeling theory

LIU Qian1, YIN Xing-Yao1, LI Chao2

1SchoolofGeosciences,ChinaUniversityofPetroleum(Huadong)，Qingdao266580,China2CNOOCResearchInstitute,Beijing100028，China

Reservoir parameters are used to describe the reservoir characteristics quantitatively. It′s important to predict reservoir parameters in reservoir characterizations. This paper proposes a method to predict reservoir parameters based on inverse modeling theory. In the framework of rock physics theory, this paper focuses on parameter prediction with inverse modeling in the reservoir parameter domain. First of all, an accurate rock physics model was established according to the characteristic of the target reservoir. Then, in the reservoir parameter domain, elastic parameters at every point were calculated to form elastic data cubes. Isosurfaces of the elastic data cubes can be calculated with the Marching Cubes algorithm. The reservoir parameter prediction was implemented by the isosurface intersection of three different elastic parameters in the same domain. Based on these, an extended inverse modeling method has also been proposed. It contains two main parts-inverse modelings in two different reservoir parameter domains and the domain transformations of the inverse modeling results. Different kinds of elastic parameters make different contributions to the accuracy of inverse modeling. An applicability evaluation method was proposed for the choice of elastic parameters as input data. A model data and a real example have been chosen to test the inverse modeling method.

Reservoir parameter; Rock physics; Inverse modeling; Reservoir parameter domain

10.6038/cjg20160931.

国家重点基础研究发展计划(973计划)项目(2013CB228604)资助.

刘倩，1988年生，女，博士研究生，主要从事地震岩石物理建模及地震波场模拟方面的研究. E-mail：liuqian88115@163.com

10.6038/cjg20160931

P631

2015-11-21，2016-01-11收修定稿

刘倩, 印兴耀, 李超. 2016. 基于逆建模理论的储层特征定量预测方法. 地球物理学报，59(9):3491-3502,

Liu Q, Yin X Y, Li C. 2016. Quantitative prediction of reservoir characteristics based on inverse modeling theory.ChineseJ.Geophys. (in Chinese),59(9):3491-3502,doi:10.6038/cjg20160931.

In the model test, there are 54 points with different reservoir properties in the original model. A rock physics model was established and several elastic parameters were calculated. The prediction result was consistent with the original model data. In the real example, the proposed method was applied to a set of data from Eastern China. A site-specific rock physics model was built according to the well data. The inverse modeling method was first validated by the application on the well data. Inverted elastic parameters were also taken as the input data of inverse modeling. The accuracy of the inverse modeling with inverted elastic data was also high enough. Based on the theory of rock physics modeling, an extended inverse modeling method in reservoir parameter domain has been proposed to predict reservoir parameters quantitatively in this paper. The accuracy of the rock physics model is the foundation of the inverse modeling. The choice of input data is very important to the stability of the inverse modeling results. So the applicability of the input data should be evaluated before the inverse modeling. Tests on model data and real data have proved the rationality and applicability of this method in the prediction of reservoir parameters.