CFD软件在流体力学教学难点中的应用研究

杨小平　王文豪　马远琼　陈佰满

(东莞理工学院　化学工程与能源技术学院，广东东莞　523808)



CFD软件在流体力学教学难点中的应用研究

杨小平王文豪马远琼陈佰满

(东莞理工学院化学工程与能源技术学院，广东东莞523808)

计算流体动力学(CFD)是通过计算机数值计算和图像显示，对包含有流体流动和热传导等相关物理现象的系统所做的分析。本文将CFD数值模拟引入到工程流体力学的多媒体教学中，针对教学中存在理论不易掌握、概念和方程较多且易混淆的特点，采用CFD软件对难于理解的流线和迹线、伯努利能量方程、层流和紊流等概念进行了数值模拟分析研究，得到易于学生理解和掌握的图像、曲线和动画，可积极调动课堂气氛，增加学生的学习兴趣，显著提高教学效果。

流体力学；流线和迹线；伯努利方程；层流和紊流；CFD模拟

能源与动力工程专业的工程流体力学基础课的特点是抽象、枯燥、难懂，是一门既有较强理论性，又有较强工程实际意义的课程，具有理论不易掌握、概念和方程较多且易混淆、对学生高等数学和物理知识及综合分析和处理问题能力的要求较高。在常规的教学环境下,学生普遍反映该课程是一门非常难于学习掌握的课程，理论知识比较抽象，流体的运动规律难于理解，且不能与具体流动现象相结合[1-4]。同时受教学条件的限制，任课教师很难形象、动态地将流体流动的各种现象讲授给学生，这样使专业课的理论知识讲解与实际现象脱节。而将CFD(数值计算流体动力学)数值模拟引入流体力学的多媒体教学中，通过计算机数值计算和图像显示的方法, 在时间和空间上定量描述流场的数值解, 从而达到对物理问题研究的目的[5-8]。它兼有理论性和实践性的双重特点,可以模拟出不同条件下的流体运动，并进行数字化演示教学，有助于学生理解流体的流动状态及运动规律。本文采用流行商用CFD软件对教学中不易理解的难点进行数值分析研究，得到适用于学生理解和掌握的图像、曲线和动画，以提高学习效果。

1　流线和迹线

迹线是流体质点的运动轨迹，也就是该流体质点在不同时刻的运动位置的连线。流线是用来描述流场中各点流动方向的曲线。它是某时刻流速场中的一条矢量线，即在此线上任意点的切线方向与该点在该时刻的速度矢量方向一致。流线是指某一时刻的，而迹线是某一质点的。在空间的某一点上，一流体质点将沿该时刻的流线方向运动，并在此流线上留下了一微段迹线，但此后由于流动的不定常性，速度的方向可能改变了，原质点将依新的流线方向运动，又在新的流线上留下了一微段迹线，如此继续下去，可见流线和迹线一般是不会重合的，但在定常流动中二者是重合的。迹线的微分方程为：

其中t是自变量，x，y，z是t的隐含数，t是单个独立变量，积分后消去t就得到迹线方程。

流线微分方程：

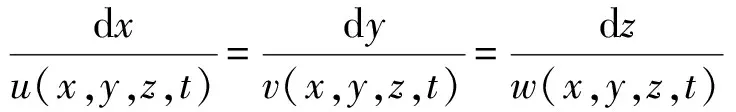
方程是关于变量(x，y，z)的两个常微分方程组，积分就得到流线。式中的时间t作为已知的参数，代表同一时刻，在积分时可以作为常数对待，其中x，y，z，t是四个独立变量。

流线微分方程和迹线微分方程表达式相似而实质不同，流线方程是反映某一瞬间流动状况的空间曲线，x，y，z是变量，积分时常把t当作已知参量对待；而迹线方程是反映某一流点在不同时刻所走的路经，t是唯一的自变量。两者不同，在一般情况下不重合。 而定常流动时，流线与迹线完全重合。迹线方程和流线方程具有不同的内容和意义，但又可以相互转化。因此在实际教学过程中，学生对流线和迹线的概念难于理解，也容易混淆。

本例采用非稳态圆柱扰流的CFD模拟来对流线和迹线进行形象化的说明，以增加学生的理解程度和学习积极性。假设圆柱的半径为0.02 m，来流速度为0.01 m/s。根据已知条件，建立管内流体流动的几何模型，划分网格，设定边界条件，网格模型如图1所示。将网格和边界条件数据文件导入CFD软件，选择求解类型，定义物理模型，设置边界条件参数和初始条件，进行数值计算，并导出数值模拟结果数据文件。

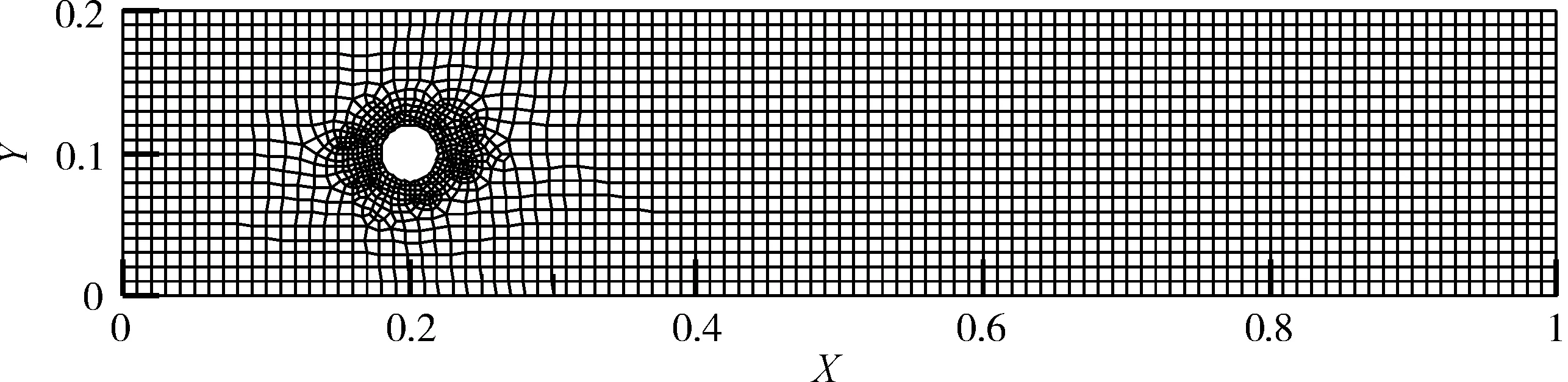
图1　网格模型

圆柱扰流为非稳态流动，在尾部会形成卡门涡街，流线会随着时间而变化。图2和图3分别表示流动时间为50 s和100 s时的流线图，由图可知，在非稳态流动时，不同时刻的速度方向是不同的，流线随着时间而变化，流线图是某一时刻的速度方向图。

图2　流动时间为50 s时的流线图

图3　流动时间为100 s时的流线图

图4位入口处不同流体质点的迹线图，表示了不同流体质点随着时间的运动轨迹。可见流线和迹线存在着本质的不同。CFD软件还可以动态演示流体质点的运动轨迹，可以较大的提升学生学习积极性和教学效果。

图4　不同流体质点的迹线图

2　伯努利方程

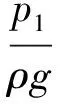
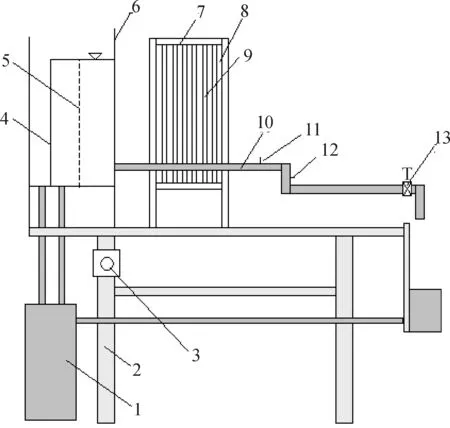
图5　自循环伯努利方程实验装置图

本例对教学实验管道进行CFD数值模拟，建立管道的物理模型，划分网格，然后输入流体流动的初始条件和边界条件进行计算。其中细管的直径为14 mm，粗管的直径为27 mm，管路总长度为1 540 mm，左边管道比右边管道高250 mm，水流进口速度设为1 m/s。计算结果可以显示整个管路的静压力、动压力、总压力等图像和数据。图6中所示为管道的静压力分布图，可以看到整个管路的静压力沿着管道逐渐减小，到出口处的静压力为零。

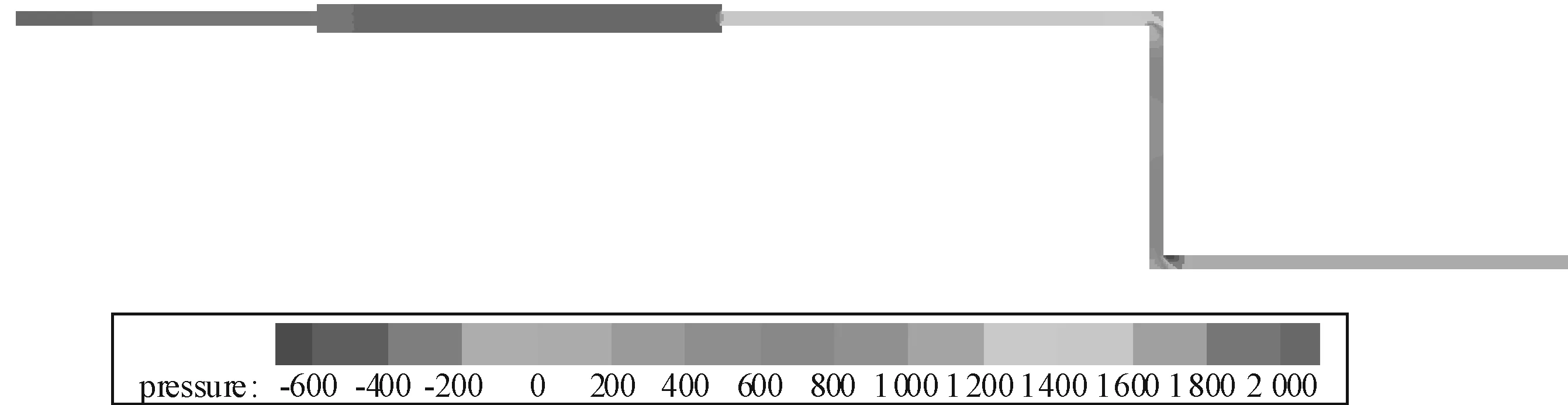
图6　管路系统的静压力等值线图

对各种压力数据进行输出和计算整理，对流体区域的总压和静压力沿着管路进行水头线的绘制，得到图7所示的以压力表示的水头线分布图。可以看到总压力水头线逐渐下降，表示流动过程中的沿程阻力能量损失；在管道突然变化的截面，总压力会下降明显，表示流动过程中的局部阻力损失。测压管水头线在管径一致的地方逐渐下降，在管径较大的位置会上升，表明此处流体的流动速度变小。在做实验过程中，学生通过测量数据可以得到各测量点的水头，通过与模拟结果比较分析，可以判断实验测量的结果是否合理和正确，具有指导实验的积极作用。

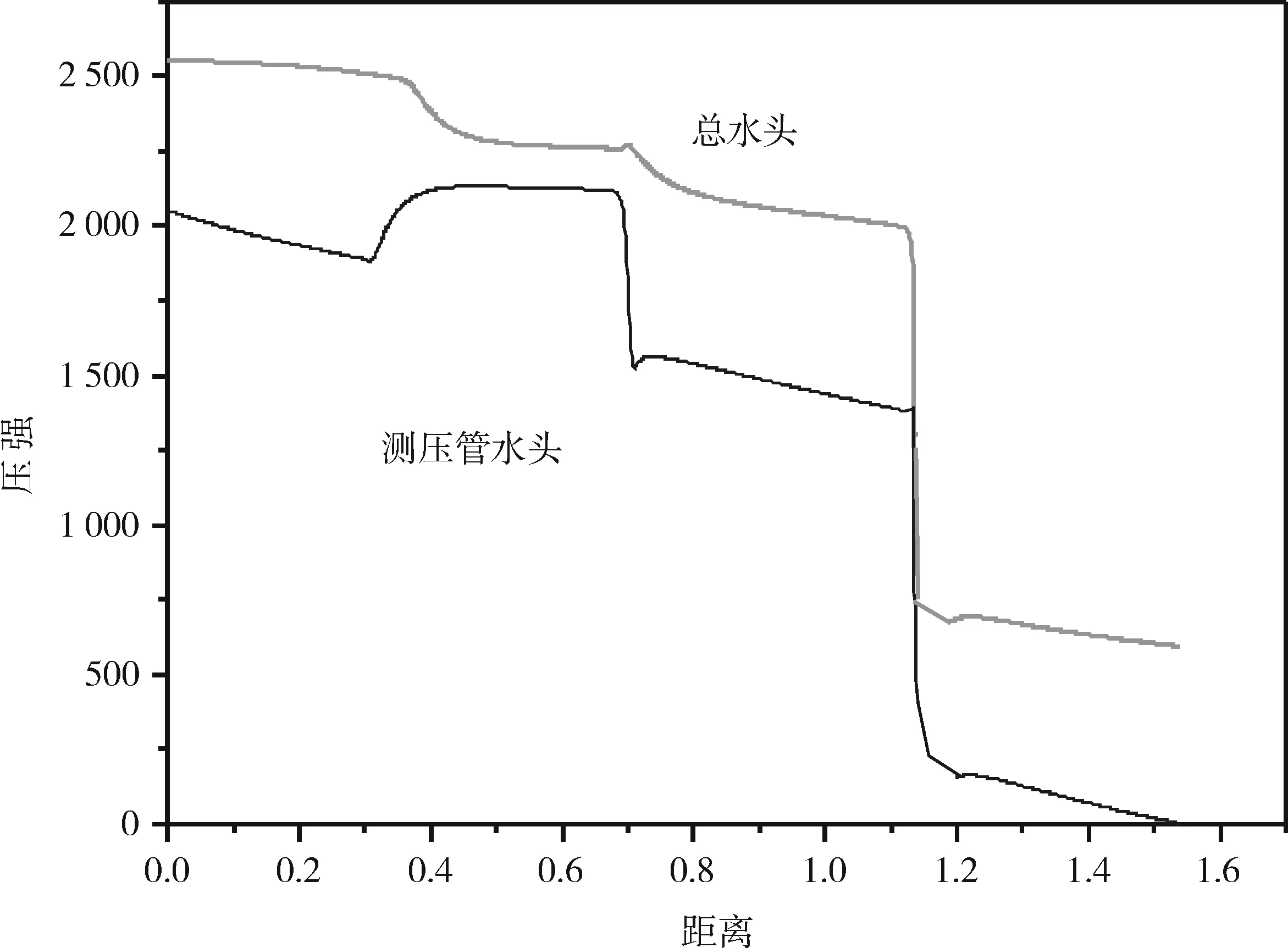
图7　总水头和测压管水头线分布图

3　层流和紊流

流体在管内流动时，其质点沿着与管轴平行的方向作平滑直线运动。此种流动称为层流。流体的流速在管中心处最大，其近壁处最小。管内流体的平均流速与最大流速之比等于0.5，根据雷诺实验，当雷诺准数Re<2 000时，流体的流动状态为层流。紊流 是指流体从一种稳定状态向另一种稳定状态变化过程中的一种无序状态。具体是指流体流动时各质点间的惯性力占主要地位，流体各质点不规则地流动。在教学过程中，学生对层流和紊流只有一个定性和抽象的理解，若想掌握不同流态时管内流动的速度分布、切应力分布、沿程阻力等知识，则需要有较好的理论知识及数学基础。而运用CFD模拟管内流体流动，可以很好地帮助学生理解流体的流动状态及管内流体的速度分布等知识。

对圆管内流体水的流动进行CFD模拟，圆管的长度为50 mm，直径为1 mm，层流时进口速度分别设定为0.1 m/s和5 m/s。对计算结果进行分析处理，可以得到图8和图9所示的出口截面的速度分布图，从图中可以看出,两种流动状态下，流体的速度均在管壁处为零，管道中心处最大，但其变化规律并不相同，层流时管内流体速度从管壁到管中心逐渐增大，圆管内横断面速度分布呈抛物线分布。而紊流时在近壁处，速度近似直线规律变化，在紊流核心区，速度比较均匀，速度梯度比较小，符合紊流速度的对数分布规律，这主要是由于紊流中横向脉动所引起的流层之间的动量交换所致。模拟结果还可以方便的查看层流和紊流时的阻力性能、切应力分布等差别。

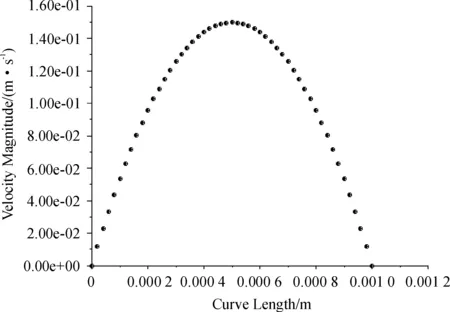
图8　层流时出口截面速度分布图

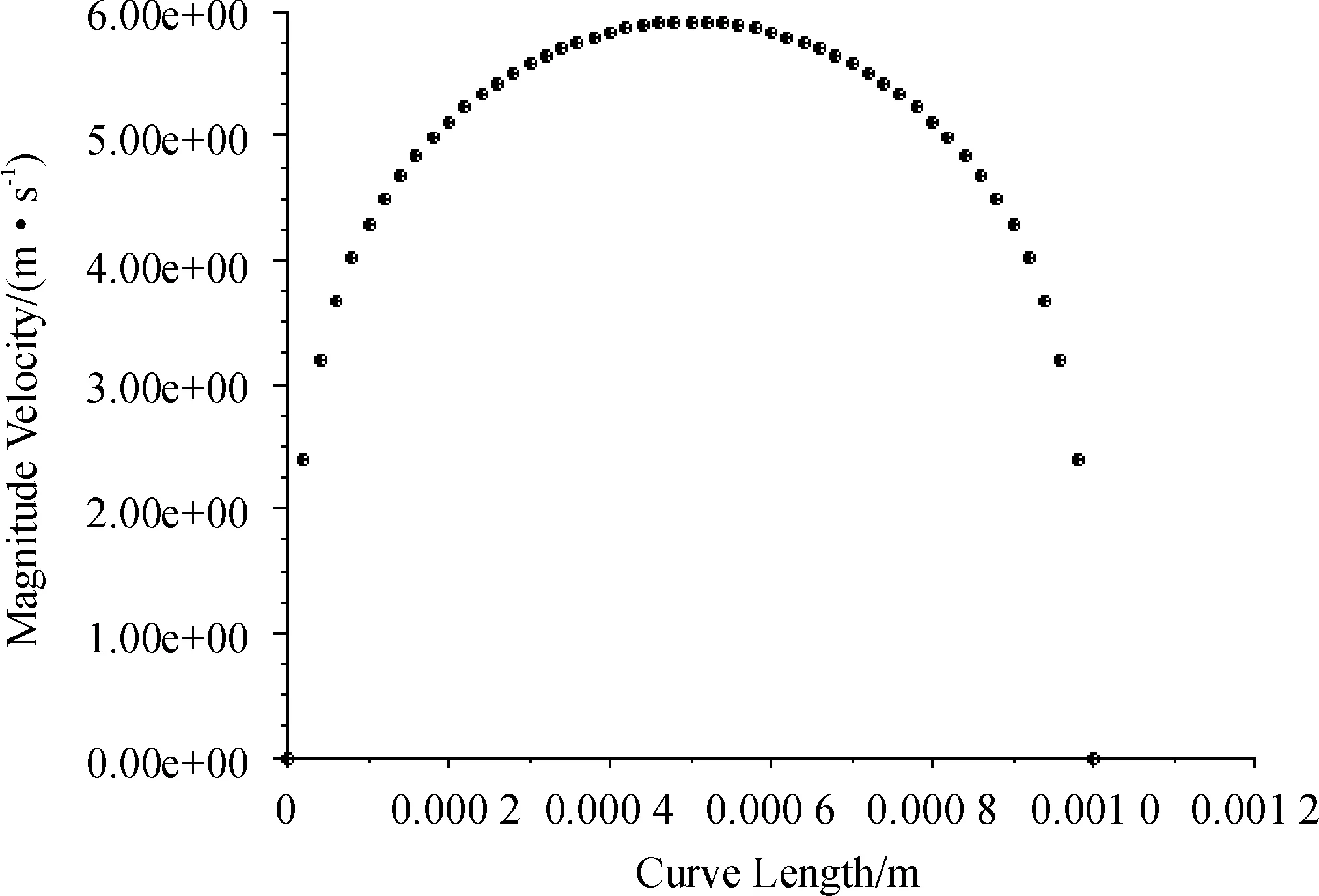
图9　紊流时出口截面速度分布图

4　结语

从上述对流线和迹线、伯努利能量方程、层流和紊流的理论分析和数值模拟可以得出，利用CFD软件可以将模拟结果以图像、曲线、动画等形式表现出来，不仅可以定性分析，还可以对流动状态进行定量的研究，得到流体运动的规律，可以充分帮助学生理解、消化与记忆。实践表明，在枯燥的理论讲解及公式推导过程中配以CFD数值模拟，可以调动课堂气氛，增加学生的学习兴趣，提高教学效果。

[1]陈庆光，张明辉，朱绪力，等. 流体力学课程教学中几个基本概念的教学方法[J]. 力学与实践，2015，37(1)：138-141.

[2]徐文娟，侯清泉，刘训涛. 多媒体技术在《工程流体力学》教学中的应用[J]. 理工高教研究，2008，27(2)：94-95.

[3]王发辉，桑俊勇，张丹. “流体力学”立体化教学体系的构建[J]. 中国电力教育，2009，(24)：102-103.

[4]陶汉中，李菊香. 关于“工程流体力学”课程多媒体教学的思考[J].中国电力教育，2010，(18)：58-61.

[5]李国威，崔俊奎. 基于FLUENT 的流体力学教学课件素材制作研究. 中国现代教育装备，2009，(5)：76-77.

[6]王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京：清华大学出版社，2004.

[7]韩占忠，王敬，兰小平. FLUENT流体工程仿真计算与实例应用[M]. 北京：北京理工大学出版社，2008.

[8]陶文铨. 数值传热学[M]. 2版. 西安：西安交通大学出版社，2002.

The Application Research of CFD Software in the Teaching of Fluid Dynamics

YANG XiaopingWANG WenhaoMA YuanqiongCHEN Baiman

(College of Chemical Engineering and Energy Technology, Dongguan University of Technology, Dongguan 523808, China )

The computational fluid dynamics (CFD) is an analysis of the system that contains the physical phenomena related to fluid flow and heat conduction through the computer numerical calculation and image display. In the teaching of engineering fluid dynamics, the theory is not easy to grasp, the concept and the equation are more and easily confused. In this paper, the CFD numerical simulation is introduced into the multimedia teaching of engineering fluid dynamics. The concepts of streamline, path line, Bernoulli equation, laminar and turbulent were analyzed by CFD numerical simulation software. The visualized fluid image, curve and animation were obtained, which can mobilize the classroom atmosphere, increase students’ interest in learning and improve teaching effect obviously.

fluid dynamics; streamline and path line; Bernoulli equation; laminar flow and turbulent flow; CFD simulation

2015-12-26

东莞理工学院教育教学改革与研究(2015)；广东省高等教育教学改革与研究(2016)。

杨小平(1979—)，男，内蒙古丰镇人，副教授，博士，主要从事流体力学、流体机械及数值计算等研究。

O303

A

1009-0312(2016)05-0118-05