基于逐日积雪深度预报的藏北草原雪灾等级评估

林志强路红亚马艳鲜

（1 西藏自治区气候中心，拉萨 850000；2 西藏自治区气象服务中心，拉萨 850000）

基于逐日积雪深度预报的藏北草原雪灾等级评估

林志强1路红亚1马艳鲜2

（1 西藏自治区气候中心，拉萨 850000；2 西藏自治区气象服务中心，拉萨 850000）

选取西藏高原北部牧区的13个气象站冬半年（11月—次年4月）的1980—2007年逐日积雪深度和最高、最低、平均气温资料，对藏北牧区草场的融雪量与气温关系进行了分析。利用线性回归模型建立融雪率和最高、最低气温的方程，给出了藏北草场的融雪日数、逐日积雪深度的计算方法，得出草场雪灾等级评估产品，实现在一场降雪后根据日常天气预报业务制作草场逐日积雪深度的预报产品，并实时评估雪灾的严重程度，为草原雪灾气象服务提供定量化参考产品。对2008—2009、2009—2010和2010—2011年的三个冬半年进行了预报效果评估，1～15d的逐日积雪深度的平均绝对误差不超过2cm；积雪日数误差不超过9d，误差在1d以内的占78.5%；雪灾等级的准确率约为84%；该方法具有较好的预报效果，能为藏北雪灾评估提供参考。该方法的缺陷在于，由于没有准确的定量降雪预报产品，故没有考虑后续降雪量的新增积雪影响。

藏北草原，积雪日数，融雪率，雪灾评估

0 引言

雪灾是西藏高原北部牧区冬春季最主要、影响最广、破坏力最大的气象灾害，积雪覆盖牧场，并且在表面结一层冰壳，使得积雪不能融化而成灾，牲畜无法吃草，膘情较差的牲畜在饥寒交迫下大批死亡，同时大雪封路、封山，给交通运输、邮政通讯、国防建设、地质测绘等造成巨大损失［1］。

由于青藏高原地处高寒地带，生态环境脆弱，人口稀少，经济发展较为滞后，雪灾对国民经济的损害尤为严重，对青藏高原雪灾的时空分布特征和环流特征的分析得到了国内气象工作者的重视，姚玉壁等［2］、董文杰等［3］、董安祥等［4］、马林等［5-6］、梁潇云等［7］、周陆生等［8］、时兴合等［9］对青藏高原不同区域牧区的冬、春、秋季雪灾的气候特征和水汽、环流特征进行了分析。在雪灾的监测和服务中，需要对雪灾的严重程度进行评估。李彰俊等［10］引入湿度对体感温度的影响以及人畜身上落雪增加的体热损耗，对Schlatter风寒指数进行了修正，对暴风雪灾害进行了有效的评估。周秉荣等［11］应用灾害学的理论和观点，对造成青藏高原雪灾的致灾因子、孕灾环境和承灾体等要素综合分析，建立从降水、积雪、成灾、灾情评价的综合判识模型。林建等［12］结合常规站点雪深资料和卫星监测的积雪覆盖率资料，主要考虑积雪厚度和持续时间对不同草场的灾情影响，建立了一套简单的雪灾监测方法。宫德吉等［13］指出在暴风雪过程中，大风、暴雪、强降温联合施虐，加剧了人畜的热损耗率，从而形成严重的冻害。姚筠等［14］利用实时雪情和灾情资料建立了安徽省单站和全省的农业经济损失定量评估模型。

在西藏高原冬春季雪灾的气象服务实践中，在一场强降雪之后，对积雪深度的变化和积雪日数估计是评估雪灾严重程度的重要参数，能够为及时抗灾救灾提供参考。在目前的研究中，融雪模式由于需要大量的地雪、雪气交界面模式参数输入［15-17］，在业务中并不适用。本文通过分析气象要素与积雪消融的关系，建立藏北草原分站的逐日积雪深度模拟模型，提出制作逐日积雪深度和积雪日数的预报方法，以准确评估雪灾严重等级，为抵御藏北草原的冬春季雪灾提供参考。

1 资料与方法

选取1980年1月—2008年6月的藏北草原13个气象站（图1）的冬半年（11月—次年4月）的地面气象观测资料，包括积雪深度、最高气温、最低气温、日平均气温等气象要素，对积雪消融速率（即一天消融的积雪厚度，以下称融雪率）与气象要素的关系进行分析。采用线性回归方法建立融雪率与气象要素的关系，建立藏北草原分站融雪率预报模型。

2 藏北草原气温-融雪率关系

气温是决定融雪率的主要因素［18-20］，为了分析藏北草原气温和融雪率的关系，选取1980年1月—2008年6月间的符合以下条件的个例：

1）前一天有积雪，而当天没有新降雪的个例；

2）去掉前一天有积雪，而当天已经完全消融的情况。

将这些个例的当天积雪减前一天的积雪，即可得到融雪率，而这些积雪都是在前一天08时至当天08时这一时段内消融的，该时段的最高、最低和平均气温均可从气象记录中得到。

分别对最高、最低和平均气温以1℃为间隔，计算每一温度区间的平均融雪率（图2），从图中可见：最高、最低和平均气温都满足准正态分布；最高、最低和平均气温与融雪率都呈线性关系，即温度越高（低），融雪率越大（小），相关系数分别为0.824、0.856和0.838，均通过0.001的显著性水平检验，其中最低气温与融雪率的关系最好；从两者的线性趋势关系上看，最高、最低和平均气温每升高1℃，积雪的融雪率分别增加0.036、0.046和0.055cm。

上面说到，校园文化是能够分作狭义上的于广义上的，这个点，我们主要讨论的是广义上的校园文化。首先，我们知道，广义上的校园文化是由精神文化、物质文化、行为文化共同构成的有机整体。首先，精神文化可以说是校园文化的核心，主要是以大学精神的形式表现。而大学精神，则是一个大学在长期的教育实践中积淀的最富有典型意义的精神特质，也可以说是大学的办学理念，例如北京大学的“兼容并包”。

由此可见，温度是一种很好的计算融雪率的指标［21-22］，以下将以温度为因子，分别对藏北草原每个气象站建立融雪率预报方程。

3 积雪深度预报方法及结果检验

考虑到日常天气预报业务中只对最高、最低气温进行预报，因此这里只建立基于最高和最低气温的模型，用线性回归方法建立融雪量ΔS与最高气温、最低气温的方程：

其中，a0、a1、a2为回归系数，Tmin、Tmax分别为当日最低、最高气温；当ΔS＜0时，ΔS=0。

对13个站分别建立回归方程，回归系数和拟合结果见表1。其中，洛隆的拟合结果只通过了0.05显著性水平检验，改则和昌都分别通过了0.01显著性水平检验，其他的拟合都通过了0.001显著性水平检验，可见采用最低和最高气温作为预报因子参数是可行的。作为例外情况，从图2中，当Tmax≥10℃或者Tmin≥0℃时，则融雪率为现有的积雪；当通过回归方程计算的融雪率为负值时，融雪率取为0。

图2 不同温度的平均融雪率分布（a）最高气温；（b）最低气温；（c）平均气温Fig. 2 Distribution of averaged snow melting rate at different temperature (a) the maximum temperature; (b) the minimum temperature; (c) average temperature

在日常业务预报产品中，仅提供24～168h（1～7d）最高、最低气温的分站定量预报结果，因此该时段的最高、最低气温采用西藏自治区气象台提供的定量预报；从延伸期预报能力［23-27］来看，目前的预报水平较低，而且在西藏自治区气象台未提供该期间的逐日温度预报的情况下，8d及其后的最高、最低气温值采用气候平均值。值得指出的是，由于目前的预报水平提供准确、定量降雪量预报尚存在较大的困难［28-30］，因此无法在积雪深度预报中对新增积雪进行考虑，因而在模型中只对在融雪过程中不再有新的降雪的简单情况进行分析。此预报模型可以提供的积雪深度预报产品包括：

表1 融雪量回归方程系数和拟合结果Table 1 The regression coefficients and fitting effects

1）直至积雪完全消融的逐日积雪厚度Ht的预报。预报方法是：

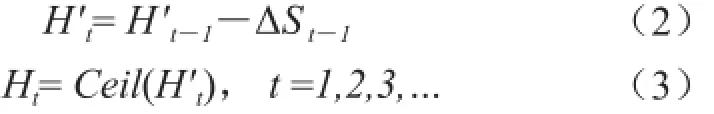
式中，H′t-1为前一天的积雪厚度，t=0即为起报时间的积雪厚度；ΔSt-1为根据式（1）由最高、最低气温得到的融雪量，考虑到积雪深度一般取整数，因此对最后的积雪厚度序列结果取不小于H′t的整数为最后结果Ht（即Ceil函数）。

考虑到温度预报有一定的不确定性，对ΔS预报中，分别对最高、最低气温取±2℃的预报偏差，由于最高气温和最低气温的回归系数a1和a2均为正数，因此即相当于融雪量ΔS的范围为：

2）持续积雪日数D预报（图3b）。由逐日积雪深度预报产品，即可得到持续积雪日数D，并可以相应地得到考虑了温度预报不确定性的持续积雪日数Dmin～Dmax，如图3a中，D=47d、Dmin=40d、Dmax=54d。

3）藏北草原的逐日积雪深度预报（图3c）。对所有站取预报日的积雪深度预报值，即可形成当日的积雪深度空间分布预报图，如从图3a中即可知安多站1998年2月3日的积雪深度预报量为12cm，考虑温度不确定性后的取值范围为9～15cm。

利用2008—2009、2009—2010和2010—2011年的三个冬半年的西藏自治区气象台逐日天气预报产品对藏北草原的逐日积雪深度预报，并制作服务产品，预报制作的标准为当藏北任意一站的当日积雪厚度≥1cm时，即启动本预报模块。

对预报产品的检验方法为：当预报时效的时段内，预报站没有新的降雪，即对其预报效果进行评估，例如如果预报的第三天又有新的降雪，那么则只对1、2d的预报产品进行评估，而不评估3d及其后的产品预报效果。

图3 1998年1月12日起报的积雪深度预报产品示例（a）安多站逐日积雪深度；（b）藏北草原持续积雪日数；（c）藏北草原24h积雪深度Fig. 3 A sample of forecast products of snow cover over Northern Tibetan Plateau, started from 12 J anuary 1998 (a) daily snow depth at Amdo Station; (b) continuous snow cover days; (c) snow depth after 24 hours

1～15d的逐日积雪深度预报绝对误差如图4a所示，可见15d内的平均绝对误差不超过2cm，其中1d有300多个样本，平均绝对误差为0.76cm；2d有约200个样本，平均绝对误差为1.11cm；3d有约180个样本，平均误差为1.05cm；平均绝对误差最大为13d，为1.65cm；在1～3d，预报误差较小，之后误差增大，但时间较长后的积雪深度较小，误差增长的幅度不大。

将一次降雪后直至雪融化完的一次过程称为一次融雪过程，以降雪当天的积雪深度作为起报日期，试报期间共有398个融雪过程，其中383个无灾，11个轻度雪灾，3个中度雪灾，1个严重雪灾；图4b给出积雪日数的预报检验结果，可见误差为0d的有194个过程，占48.7%；误差为1d的有119个过程，占29.9%；误差为2d的有43个，占10.8%；误差为3d以上的有42个，占10.5%；最大误差为9d，共有3个过程；积雪日数预报的平均误差约为1.1d。

图4 积雪深度与积雪日数预报效果评估（a）1～15d积雪深度预报绝对误差；（b）积雪日数预报误差Fig. 4 The assessments of forecast effects(a) the averaged absolute error of daily snow depth on 1-15 days; (b) the absolute error of days with continuous snow cover

4 雪灾等级评估

根据第三节建立的积雪深度预报结果，可以对雪灾严重等级进行评估（图5）。评估一次雪灾的严重程度不仅取决于这次雪灾的积雪深度，还取决于这次雪灾中积雪的持续时间，例如，初春和初夏两次降雪过程后，积雪深度均为20cm，由于初春的温度较低，融雪较慢，即使没有后续的降雪，积雪时间可能达到10d以上，因此形成了一次严重雪灾；而初夏由于温度高，积雪很快消融，可能持续积雪日数仅为1～2d，因此就不会对农牧业生产形成很大的影响，不会造成雪灾。因此，这里综合利用逐日积雪深度H和持续积雪日数D的预报，对雪灾的等级进行评估，雪灾的评级采用假拉等［31］定义的雪灾强度等级（表2），由图3a即可知此次雪灾程度为严重雪灾。

图5 1998年1月12日藏北草原雪灾等级评估Fig. 5 The evaluation of snowstorm intensity levels for 12 J anuary 1998

表3给出了2008—2009、2009—2010和2010—2011年的三个冬半年的雪灾等级估计结果，有334个过程的评估等级与实际等级一致，占84%；有51个过程评估等级与实际等级差1级，占13%，其中5个评估等级比实际等级弱1级，46个比实际等级强1级；13个过程评估等级比实际等级强2级以上，没有过程评估等级比实际等级弱2级以上。

表2 雪灾强度等级[31]Table 2 The snowstorms intensity levels[31]

表3 雪灾等级评估Fig. 3 Assessment of snowstorm intensity evels

5 结论与讨论

1）气温与融雪率都呈线性关系，最高、最低和平均气温每升高一度，积雪的融雪率分别增加0.036、0.046和0.055cm；采用最高和最低气温利用线性回归方法建立藏北草原分站融雪率回归方程，除了洛隆、昌都和改则拟合结果分别通过0.05、0.01和0.01显著性检验外，其他各站均通过0.001显著性水平检验；

2）基于最高、最低气温和融雪率的回归模型，利用日常业务预报产品和气候平均值，可以提供包括逐日积雪深度、积雪日数和雪灾严重等级评估等产品，该方法没有考虑后续降雪量的新增积雪影响，只是在假定没有新增积雪的情况下，在未来可能温度影响下积雪的消融速度；

3）对2008—2009、2009—2010和2010—2011年的三个冬半年的预报结果15d内的平均绝对误差不超过2cm ；积雪日数误差不超过9d，误差在1d以内的占78.5%；雪灾等级评估的准确率约为84%。

本文基于最高、最低气温建立了藏北草原融雪率预报方程，利用业务天气预报产品和气候平均状况建立了积雪深度预报方法，并在此基础上建立了雪灾等级的评估。由于重点考虑了方法的业务应用，因此对积雪融化速度的预报上没有结合风速、日照、相对湿度、地温等其他影响因素，这在一定程度上可能影响了积雪融化预报的准确率。更重要的是，由于目前定量降水及降雪—积雪深度转换的预报准确率不高，因此本文没有考虑起报日后的新降雪对雪灾等级的影响，这在一定程度上影响了预报产品的服务效果。在服务过程中，根据中、长期预报（定性）结论，由预报和服务值班人员对今后的天气状况进行描述，以修正此缺陷，如何提高产品的定量程度和准确度还有待进一步的研究。

［1］ 刘光轩. 中国气象灾害大典—西藏卷. 北京： 气象出版社， 2008.

［2］ 姚玉璧， 余优森. 青藏高原东北边缘牧区雪灾的研究. 气象， 1994，20（2）： 47-51.

［3］ 董文杰， 韦志刚， 范丽军. 青藏高原东部牧区雪灾的气候特征分析. 高原气象， 2001， 20（4）： 402-406.

［4］ 董安祥， 瞿章， 尹宪志， 等. 青藏高原东部雪灾的奇异谱分析. 高原气象， 2001， 20（2）： 214-219.

［5］ 马林， 马元仓， 王文英， 等. 青藏高原东部牧区秋季雪灾天气的形成及预报. 高原气象， 2001， 20（4）： 407-414.

［6］ 马林， 张青梅， 赵春宁， 等. 青藏高原的东部牧区春季雪灾天气的形成及其预报. 自然灾害学报， 2003， 12（3）： 61-68.

［7］ 梁潇云， 钱正安， 李万元. 青藏高原东部牧区雪灾的环流型及水汽场分析. 高原气象， 2002， 21（4）： 359-367.

［8］ 周陆生， 李海红， 汪青春. 青藏高原东部牧区大-暴雪过程及雪灾分布的基本特征. 高原气象， 2000， 19（4）： 450-458.

［9］ 时兴合， 李生辰， 李栋梁， 等. 青海南部冬季积雪和雪灾变化. 气候变化研究进展， 2007， 3（1）： 36-40.

［10］ 李彰俊， 宫春宁， 姜学恭， 等. 风寒指数的修订及其在暴风雪灾害评估中的应用. 气象， 2007， 33（S1）： 3-9.

［11］ 周秉荣， 申双和， 李凤霞. 青海高原牧区雪灾综合预警评估模型研究. 气象， 2006， 32（9）： 106-110.

［12］ 林建， 范蕙君. 内蒙古雪灾监测方法研究. 气象， 2003， 29（1）：27-31.

［13］ 宫德吉， 李彰俊. 内蒙古暴风雪灾害及其形成过程. 气象， 2001，27（8）： 19-23.

［14］ 姚筠， 马晓群， 许莹， 等. 2008年安徽省雪灾农业影响定量评估研究. 气象， 2010， 36（1）： 85-90.

［15］ 马虹， 刘一峰， 胡汝骥. 天山季节性积雪的能量平衡研究和融雪速率模拟. 地理研究， 1993， 12（1）： 87-93.

［16］ 陈肖柏， 张永萍. 南极长城站积雪及其消融过程. 南极研究，1991， 3（3）： 8-14.

［17］ 车宗玺， 金铭， 张学龙， 等. 祁连山不同植被类型对积雪消融的影响. 冰川冻土， 2008， 30（3）： 392-397.

［18］ 周秉荣， 李凤霞， 申双和， 等. 青海高原雪灾预警模型与GIS空间分析技术应用. 应用气象学报， 2007， 18（3）： 373-379.

［19］ 韩海东， 王建， 王欣， 等. 科其喀尔冰川表渍区冰崖消融的度日因子研究. 冰川冻土， 2009， 31（4）： 620-627.

［20］ 柯丹， 汪玲玲， 牛生杰， 等. 基于常规气象资料融雪模式的建立及应用. 大气科学学报， 2010， 33（5）： 555-560.

［21］ 方乾， 于波， 沈树勤， 等. 新一代天气预报业务流程. 北京： 气象出版社， 2001.

［22］ 章国材， 矫梅燕， 李延香， 等. 现代天气预报技术和方法. 北京： 气象出版社， 2007.

［23］ 张存杰， 董安祥. 对T63L16所作月延伸预报准确率的评估. 气象，1998， 24（10）： 38-42.

［24］ 穆海振， 徐家良. 卡尔曼滤波方法在动力延伸预报产品释用中的应用. 气象， 2000， 26（7）： 20-22.

［25］ 林纾， 李维京， 陈丽娟. 月动力延伸预报产品在甘肃省的释用及评估. 气象， 2004， 30（10）： 22-26.

［26］ 丁一汇， 梁萍. 基于MJO的延伸预报. 气象， 2010， 36（7）： 111-122.

［27］ 钱维宏. 中期：延伸期天气预报原理. 北京： 科学出版社， 2012.

［28］ 矫梅燕， 龚建东， 周兵， 等. 天气预报的业务技术进展. 应用气象学报， 2006， 17（5）： 594-602.

［29］ 罗兴宏. 那曲冬季雪灾天气的500hPa形势场的客观分型. 气象，1995， 21（1）： 40-43.

［30］ 王雨， 闫之辉. 2004年汛期主客观降水预报检验. 热带气象学报，2006， 22（4）： 331-339.

［31］ 假拉， 杜军， 边巴扎西. 西藏气象灾害区划研究. 北京： 气象出版社， 2008.

Snowstorm Intensity Assessment in the Grassland over Northern Tibetan Plateau Based on Daily Snow Depth Forecasting

Lin Zhiqiang1， Lu Hongya1， Ma Yanxian2
（1 Climate Center of Tibet Autonomous Region， Lhasa 850000 2 Weather Service Center of Tibet Autonomous Region， Lhasa 850000 ）

The relationship between snow melting rate （SMR） and temperature is analyzed by using ground observation data during the winter half year from current November to the next April in years from 1980 to 2007， at 13 weather stations over the Northern Tibetan Plateau. The daily products of snow cover days， snow depth and snowstorms intensity level are offered based on the linear regression model between SMR and the maximum temperature， minimum temperature. This method may be applied to assessing the snowstorm severity on time， and providing quantitative products in meteorology for the grassland snowstorm. In assessments for three winter half years of 2008-2009， 2009-2010 and 2010-2011， the averaged absolute forecast-error of daily snow depth is less than 2cm for 1-15 days； of snow cover days is less than 9d， of which 78.5% errors are not more than 1 day； of the accuracy of snowstorms intensity level is about 84%. So， it has a better forecast function for the snow disaster assessment in the Northern Tibet. The defect is that no consideration of the new snow cover for the later snowfall， because there is no accurately quantitative snowfall forecasting products.

the grassland of Northern Tibetan Plateau， snow cover days， snow melting rate， snowstorm intensity assessment

10.3969/j.issn.2095-1973.2016.05.004

2014年7月25日；

2014年9月4日

林志强（1982—），Email： linzq82@gmail.com

资助信息： 公益性行业（气象）科研专项（GYHY201106005）；中国气象局新技术推广项目（CMATG2010M25）