有限元分析压电半空间接触问题
高鹏博,刘铁军
(内蒙古工业大学 理学院力学系,内蒙古呼和浩特,010051)
有限元分析压电半空间接触问题
高鹏博,刘铁军★
(内蒙古工业大学 理学院力学系,内蒙古呼和浩特,010051)
压电材料作为一种拥有优越机电耦合性能的智能材料,其力学性能受到了研究者的广泛关注。本文采用有限元方法分析压电半空间在刚性球形压头和刚性圆柱平底压头作用下的压痕响应。文中假定两种形状的刚性压头均为绝缘体压头。利用有限元软件ANSYS,本文分析了在荷载作用下,压电材料在球形和圆柱形压头作用下的压入深度、接触半径、表面接触应力和接触区域电势曲线。另外,本文还利用数值结果对理论解进行验证。
压电半空间,接触问题,有限元分析
0 引言
压电材料[1]是一种能够实现电能和机械能相互转化的智能材料,已被广泛用来制造压电传感器和驱动器。优越的力电转化性能,使其在智能结构和微电机系统中发挥着重要的作用[2]。接触问题是研究固体间相互接触时在接触区的作用状况,包括位移、应变和应力,以及由此引起的强度分析方面的问题。接触问题体在研究接触表面的破坏机理,通过压痕实验测定材料力学性能等方面具有重要的意义。Johnson[3]则在其经典著作中给出了弹性体材料的接触问题分析方法。最近,Giannakopoulos等[4][5]用Hankel积分变换方法得到了压电材料半空间在导电体和绝缘体压头作用下的三维接触问题的解析解,同时,该文还针对三种商业压电材料进行了有限元分析,并对理论解与Abaqus有限元解进行比较。该文主要侧重理论分析,未给出有限元分析的详细过程,以及应力分布,压痕-压力关系以及压力和电势的关系曲线。现在,有限元软件的使用越来越广泛,如王光建[6]基于ANSYS软件分析了双螺旋副斜齿轮强度,为材料力学性能问题的解决提供了新的思路。有限元在有限元分析接触问题的方面,孙林松等[7]列举了三种数值方法来分析接触问题;李一耕[8]通过ANSYS进行了推力球轴承赫兹接触问题的计算,所得结果与赫兹理论解进行对比;王振波[9]通过有限元方法分析了MEMS涂层的接触问题,为MEMS涂层的可靠性设计提供了理论基础。赵亚素[10]基于ANSYS软件分析了非均匀涂层在均布荷载作用下的接触问题
本文利用大型有限元分析软件ANSYS,分析压电半空间的三维无摩擦接触问题。通过对三种目前可供商业使用的压·电材料进行分析和建模,求解了在特定荷载值作用下,三种压电材料在圆柱形和球形压头作用下的压入深度、表面接触应力和电势。
1 问题的描述
三维压电半空间接触问题的几何模型如图1所示,本文主要研究平底圆柱 (图1a)和球形(图1b)两种几何形状刚性压头作用于压电半空间的接触问题。柱坐标体系如图所示,平面半径方向由r表示,外法线方向由z表示。压电半空间的尺寸远大于压头尺寸。接触面为z=0的平面,由作用力P引起的压入深度为δ0,同时,接触半径为a。压电材料受压的极化轴与z轴一致。
2 有限元模型建立及求解
本文针对三种可供商业使用的压电材料PZT-4、BaTiO3和PZT-5A进行分析。三种压电材料半空间在刚性压头作用下的接触问题,三种压电材料性能参数参见表1。
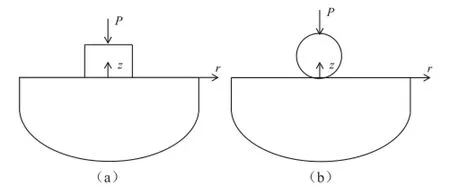
图1 压电半空间受刚性圆柱形压头(a)和刚性球形压头作用(b)Fig.1 Piezoelectric half-space with the action of rigid flatcylindrical punch(a) or a rigid sphere punch(b)

表1 压电半空间材料性能参数[11][12]Tab.1 The performance parameters of piezoelectric half-space
2.1 刚性平底圆柱压头算例
刚性圆柱压头半径为0.2m,压电半空间半径为2m,厚度为2m。荷载P分别取0.2N,2N,5N,10N,15N,20N,25N,30N,35N,40N,50N共12组模拟。NSYS建模过程中刚性压头采用SOLID185单元,压电半空间采用SOLID5耦合场单元。如图2所示,因为是轴对称模型,建模时将模型简化为1/4模型,提高运算效率。网格划分时采用六面体网格,并在接触区域进行网格细化,提升计算精度。接触对设置将压头下表面设置为目标面,压电半空间上表面设置为接触面,接触表现设置为Standard,接触方向设置为On nodes-Normal from contact。PZT-5A压电半空间在P=2N时平底圆柱压头作用下的压入深度、表面接触应力与电势的云图分别见图3、图4与图5。
2.2 刚性球形压头算例

图2 平底圆柱压头作用下接触问题模型与网格划分Fig.2 The model and meshing of contact problem with flat cylinder punch
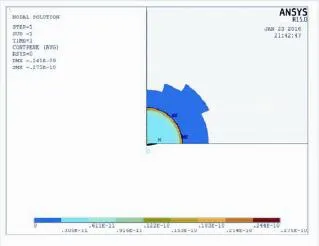
图3 平底圆柱压头作用下 PZT-5A半空间在P=2N时接触表面的压入深度云图Fig.3 The cloud map of penetration in the contact surface of PZT-5A half-space with the action of flat cylinder punch when P=2N
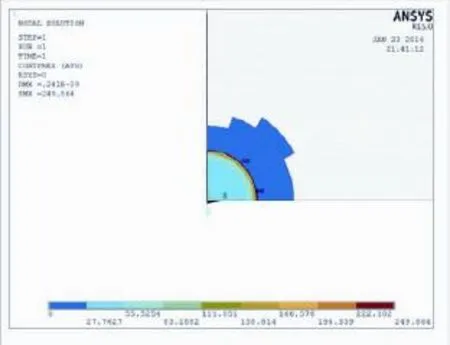
图4 平底圆柱压头作用下PZT-5A半空间在P=2N时表面接触应力云图Fig.4 The cloud map of contact pressure in the contact surface of PZT-5A half-space with the action of flat cylinder punch when P=2N
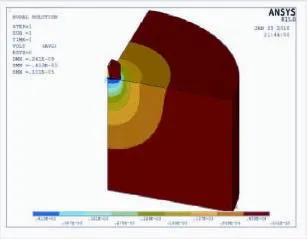
图5 平底圆柱压头作用下PZT-5A半空间在P=2N时电势云图Fig.5 The cloud map of electric potential of PZT-5A halfspace with the action of flat cylinder punch when P=2N
刚性球形压头半径R=0.2m,压电半空间半径为2m。施加的荷载P与刚性圆柱形压头相同。球形压头采用solid187单元,压电半空间采用耦合场solid98单元,建立1/4模型。如图6所示,因为刚性球形压头与压电半空间接触区域较小,需要在接触区域附近的网格划分足够密,因此采用四面体网格。接触对设置将压头下表面设置为目标面,压电半空间上表面设置为接触面,接触表现设置为Standard,接触方向设置为On nodes-Normal from contact。PZT-5A压电半空间在P=0.2N时平底圆柱压头作用下的压入深度、表面接触应力与电势的云图分别见图7、图8与图9。
3 数值结果与分析
以下将对圆柱形压头和球形压头作用下的接触应力分布,压力-压痕曲线以及压力-电势曲线进行分析。
首先,为了验证结果的正确性,本文计算了球形压头最大压入深度、接触半径。计算结过如表2所示,本文的结果与文献[13]符合较好。
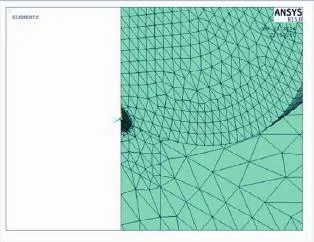
图6 球形压头作用下接触区域附近网格划分细节Fig.6 The detail of meshing near the contact area with the action of sphere punch
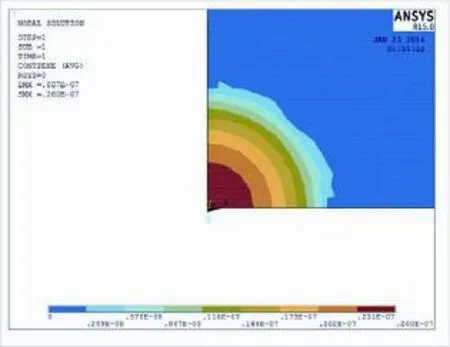
图7 球形压头作用下PZT-5A半空间在P=0.2N时接触表面的压入深度云图Fig.7 The cloud map of penetration in the contact surface of PZT-5A half-space with the action of sphere punch when P=0.2N
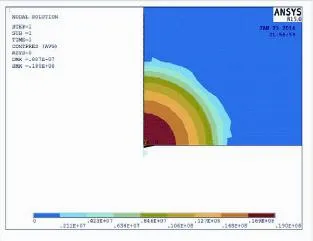
图8 球形压头作用下PZT-5A半空间在P=0.2N时表面接触应力云图Fig.8 The cloud map of contact pressure in the contact surface of PZT-5A half-space with the action of sphere punch when P=2N
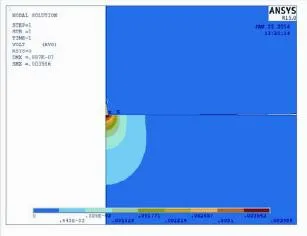
图9 球形压头作用下PZT-5A半空间在P=0.2N时Fig.9 The cloud map of electric potential of PZT-5A halfspace with the action of sphere punch when P=2N

表2 球形压头作用下最大压入深度、接触半径与理论值的比较Tab.2 Comparison between numerical results and theoretical solution of max penetration and contact radius with the action of sphere punch
图10和图11给出了三种不同压电材料在圆柱形压头作用下的压痕和接触应力分布。从图10中可以发现,同样作用力作用下,平底圆柱压头压入深度从大到小依次为PZT-5A材料、PZT-4材料、Ba-TiO3材料。从图11中可以发现,相同作用力作用下,三种材料的表面接触应力数值接近,在接触区域内变化较为平缓,接触边界处同时存在大幅度的急剧增高,这一现象与解析解结论中接触边界存在的奇异性相吻合。
图12和图13给出了三种不同压电材料在平压头作用时,压入深度δ0与压力P以及最大电势φ0与压力P的关系曲线。从图12中可以发现,δ0与P呈线性关系。相同荷载作用下,PZT-5A材料产生的δ0最大,而BaTiO3产生的δ0最小。从图12中可以看到,φ0与P同样呈现出线性关系。在相同荷载作用下,PZT-5A材料产生较大的电势而BaTiO3产生较小的电势。
如图14和图15所示,球形压头作用下的最大压入深度δ0与最大接触应力P0被给出。从图中可以发现,相同作用力作用下,产生δ0由大到小的压电材料依次为PZT-5A、PZT-4、BaTiO3。而产生的最大应力则刚好相反。
图16和17分别给出了当荷载P=0.2N时,压电半空间表面的应力分布和电势分布。从图中可以发现,最大接触应力P0出现在接触区域的中心。其中,BaTiO3材料产生的最大接触应力最大而接触区半径最小。PZT-5A材料产生的最大接触应力最小而接触区域半径最大。如图17所示,同样条件下,最大电势φ0同样出现在接触区域中心,电势沿径向逐渐降低;电势由大到小依次为PZT-5A、PZT-4、BaTiO3,整体趋势与理论结果相同。
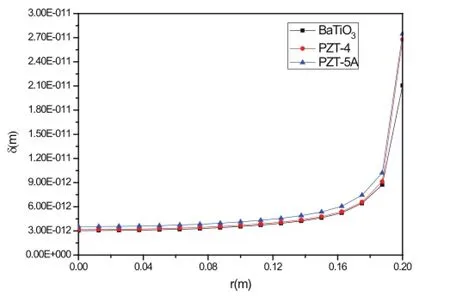
图10 P=2N平底圆柱压头作用下压电半空间接触面压入深度Fig.10 Penetration at contact area of piezoelectric half space under the flat cylinder punch when P=2N
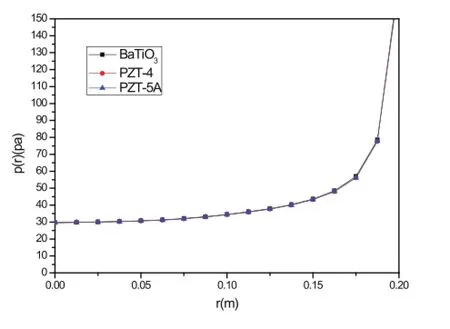
图11 P=2N平底圆柱压头作用下压电半空间表面接触应力分布Fig.11 Contact pressure at contact area of piezoelectric half space under the flat cylinder punch when P=2N
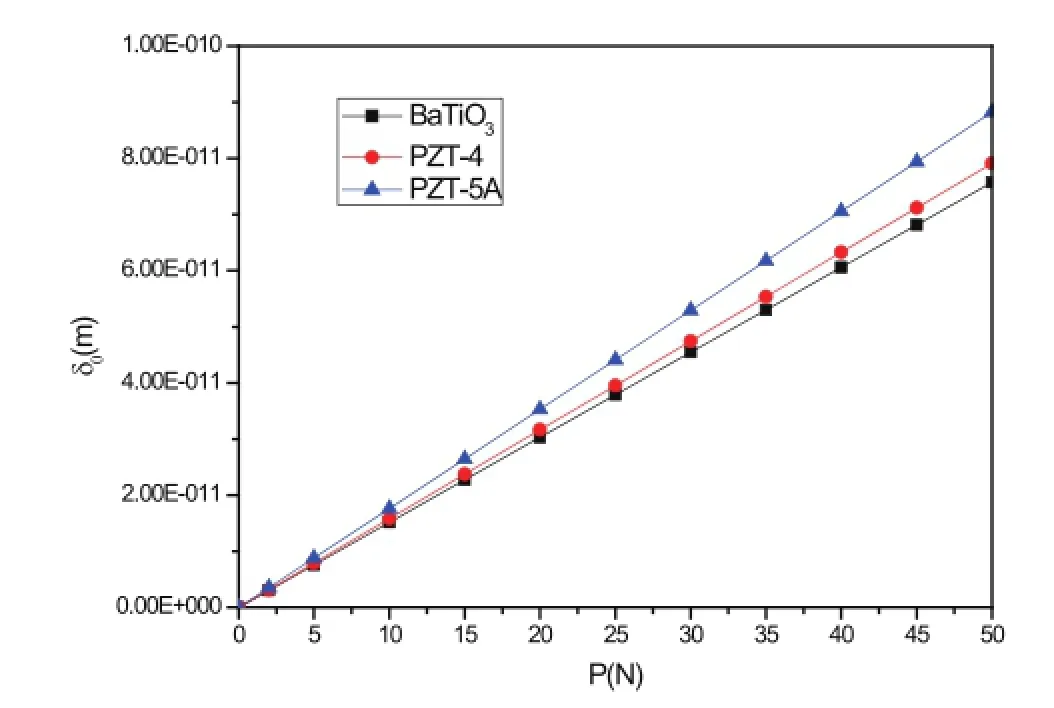
图12 平底圆柱压头作用下r=0处压入深度与作用力的关系Fig.12 The relationship between penetration at the point of r=0 and applied force with the action of flat cylinder punch
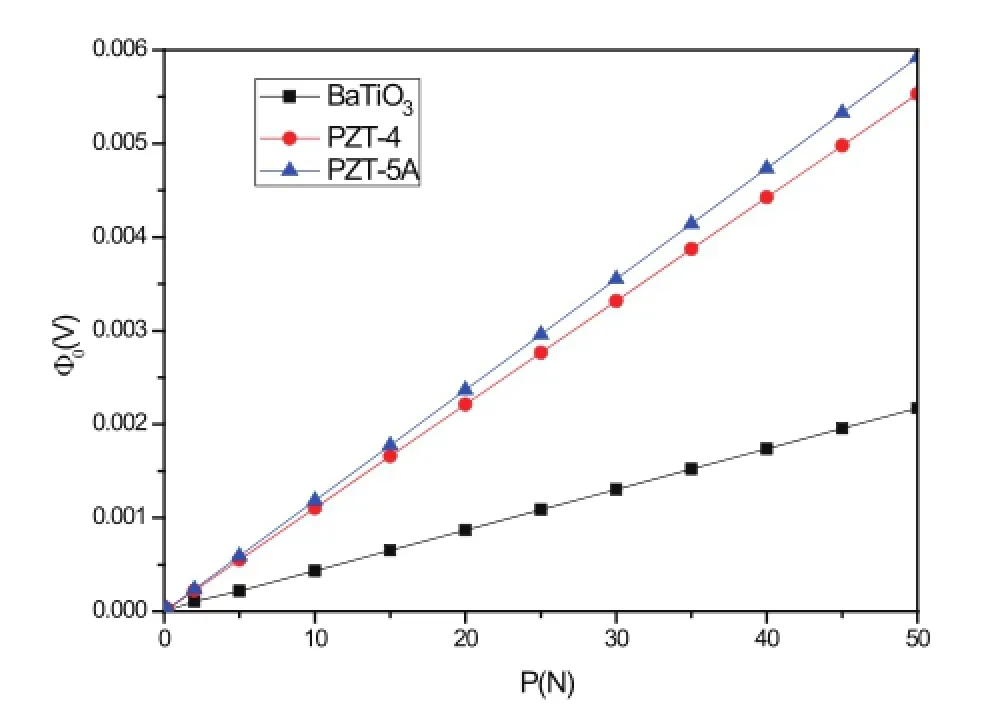
图13 平底圆柱压头作用下压电半空间最大电势与作用力的关系Fig.13 The relationship between the max electric potiential and applied force with the action of flat cylinder punch
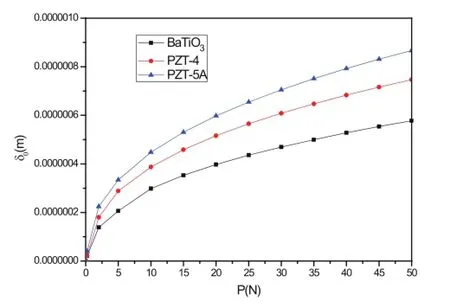
图14 球形压头作用下最大压入深度与作用力的关系Fig.14 The relationship between the max penetration andapplied force with the action of sphere punch
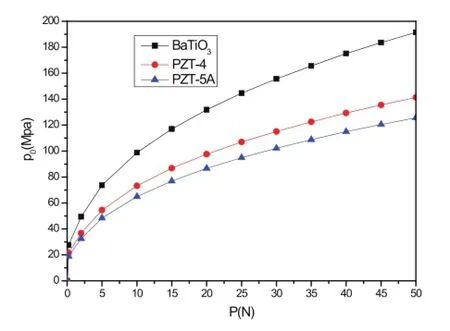
图15 球形压头作用下最大表面接触应力与作用力的关系Fig.15 The relationship between the max contact pressure and applied force with the action of sphere punch
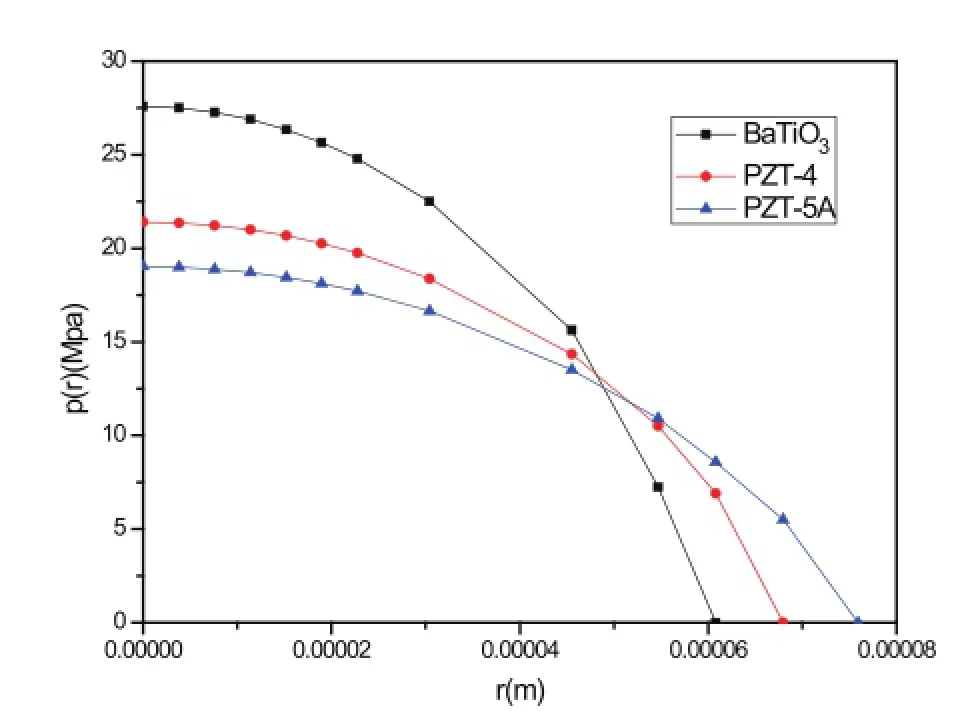
图16 P=0.2N球形压头作用下压电半空间表面接触应力分布Fig.16 Contact pressure at contact area of piezoelectric half space under the sphere punch when P=2N
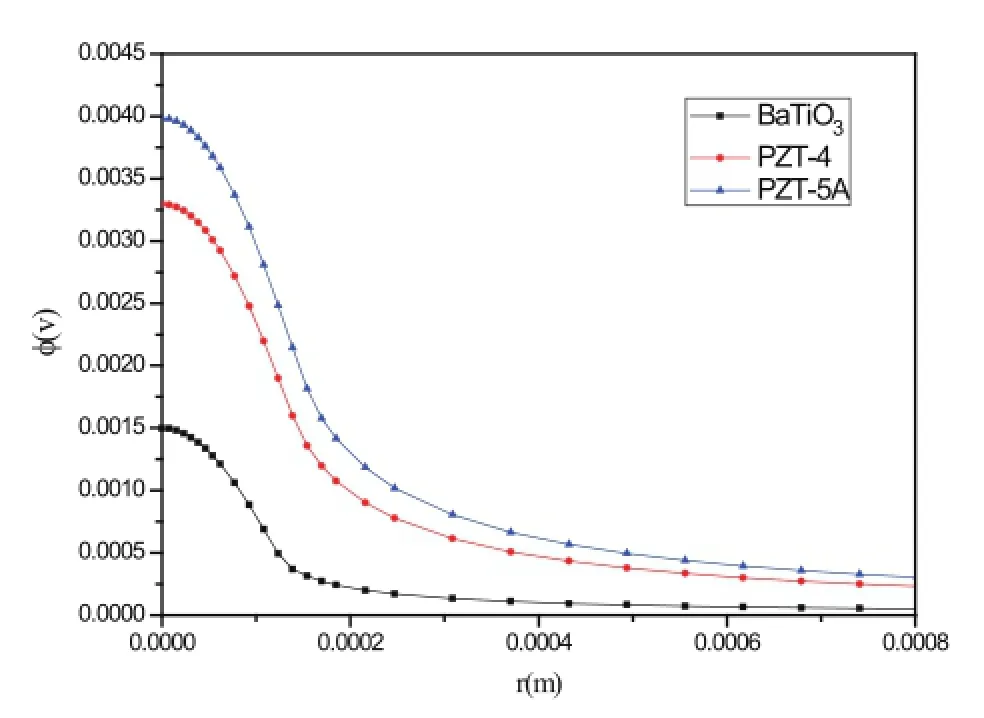
图17 P=0.2N球形压头作用下压电半空间表面电势分布Fig.17 Electric potential at the surface of piezoelectric half space under the sphere punch when P=2N
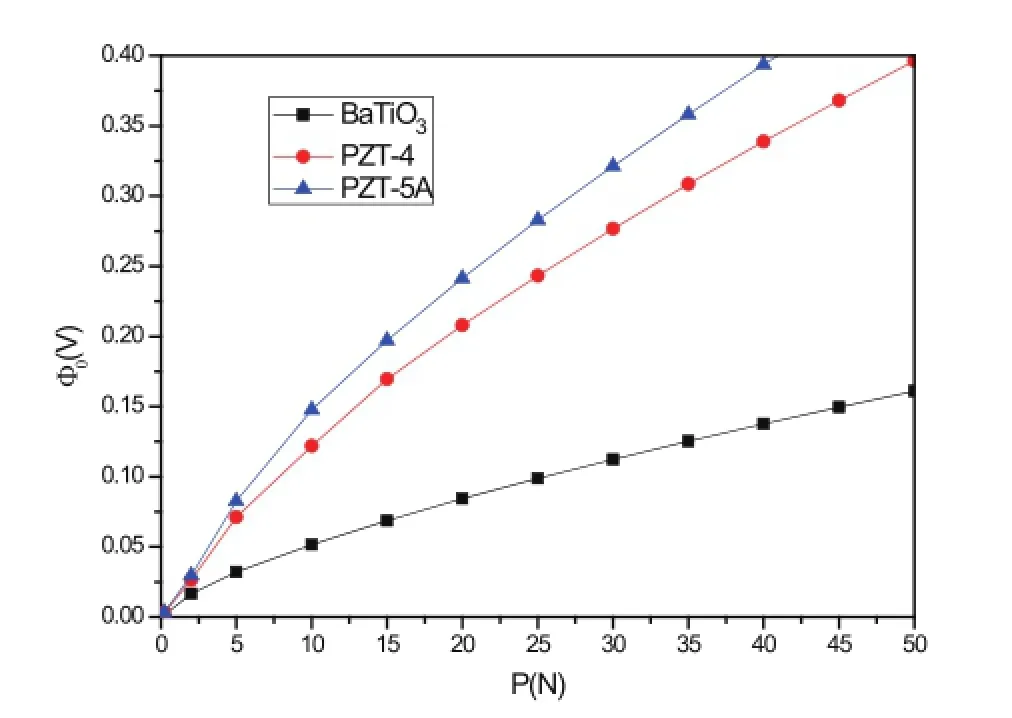
图18 球形压头作用下最大电势与作用力的关系Fig.18 The relationship between the max electric potiential and applied force with the action of cylinder punch
图18给出了最大电势φ0与作用力P的关系曲线。从图中可以看出,在相同荷载作用下,Ba-TiO3材料产生的电势最小,而PZT-5A产生的结果最大。
4 结论
利用ANSYS软件模拟接触问题可以得到比较精确的结果。
相同荷载作用下,BaTiO3压电材料产生较大的应力分布和较小的最大压痕,而PZT-5A压电材料产生较小的应力分布和较大的压痕。
在相同荷载作用下,PZT-5A材料产生较大的电势,PZT-4材料产生电势次之,而BaTiO3材料产生的电势较小。
[1] Jaffe H. Piezoelectric Ceramics[J]. Journal of the American Ceramic Society,1958,41(11):494-498
[2] Berlincourt D. Piezoelectric ceramics:Characteristics and applications[J]. The Journal of the Acoustical Society of America,1981,70(6):1586-1595
[3] Johnson K L. Contact Mechanics [M]. UK;Cambridge University Press,1985.
[4] Giannakopoulos A E,Suresh S,Alcala J. Spherical indentation of compositionally graded materials[J]. theory and experiments. Acta Mater.1997,45(4):1307-1321
[5] Giannakopoulos A E. Strength Analysis of Spherical Indentation of Piezoelectric Materials[J]. Journal of Applied Mechanics,2000,67(2):409-416.
[6] 王光建,熊正清. 基于ANSYS的双螺旋副斜齿轮强度分析[J]. 新型工业化,2013,3(9):47-52. Wang Guangjian,Xiong Zhengqing. Strength Analysis of double-helical Bevel Gear Based on ANSYS[J]. The Journal of New Industrialization,2013,3(9):47-52.
[7] 孙林松,王德信,谢能刚. 接触问题有限元分析方法综述[J]. 水利水电科技进展,2001,21(3):18-20. Sun Songlin,Wang Xinde,Xie Nenggang. A Summary of Finite Element Analysis for Contact Problems[J]. Advanced in Science and Technology of Water Resources,2001,21(3):18-20.
[8] 李一耕,陈锦江,龙超,等. 基于ANSYS的球轴承赫兹接触问题有限元分析[J]. 机械研究与应用,2011,5:35-37. Li Yigeng,Chen Jingjiang,Long Chao,et al. Finite element analysis of Hertz contact problem in ball bearing based on ANSYS[J]. Mechanical Research and Application,2011,5:35-37.
[9] 王振波. MEMS涂层接触问题的有限元分析[D]. 北京;北京理工大学,2015:1-14.
Wang Zhengbo. FEA on Contact Problems of MEMS coating[D]. Beijing;Beijing Institude of Technology,2015,1-14.
[10] 赵亚素,刘铁军,蒋雨明. ANSYS求解圆形均布荷载作用下非均匀土层表层位移[J]. 新型工业化,2014(9):30-33. Zhao Yasu,Liu Tiejun,Jiang Yuming. Ansys for Surface Displacement of Non-Homogeneous Soil Layer with Circular Uniformly Distributed Load[J]. The Journal of New Industrialization,2014(9):30-33.
[11] Wang J H,Chen C Q,Lu T J. Indentation responses of piezoelectric films[J]. Journal of the Mechanics & Physics of Solids,2008,56(12):3331-3351.
[12] Bechmann R. Elastic,Piezoelectric,and Dielectric Constants of Polarized Barium Titanate Ceramics and Some Applications of the Piezoelectric Equations[J]. Journal of the Acoustical Society of America,1956,28(3):347-350.
[13] Giannakopoulos A E,Suresh S. Theory of Indentation of piezoelectric materials[J]. Acta Material 1999,47(7):2153-2164.
Finite Element Method for Contact Problem of Piezoelectric Half-space
GAO Peng-bo, LIU Tie-jun
(Department of mechanics, school of science, Inner Mongolia University of Technology, Hohhot, 010051 China)
Piezoelectric material is a kind of intelligent material. It has the excellent coupled mechanical-electrical characteristics. The mechanical performance of piezoelectric materials has
extensive attention of the researchers. In this paper, the indentation responses problems of piezoelectric half-space under a rigid sphere punch or a rigid flat cylindrical punch are considered by using the finite element methods. It is assumed that two kinds of punches are insulated. The finite element software package ANSYS is used to calculate the indentation depth, contact radius, surface contact pressure and electric potential of the piezoelectric materials under the sphere and cylindrical punch under the applied load. Otherwise, this paper gives the numerical results to verify the theoretical solution.
Piezoelectric half-space; Contact problems; Finite element analysis
10.3969/j.issn.2095-6649.2016.02.005
GAO Peng-bo, LIU Tie-jun. Finite Element Method for Contact Problem of Piezoelectric Half-space[J]. The Journal of New Industrialization, 2016, 6(2): 27-33.
内蒙古自然科学基金(2012MS0119),内蒙古自治区“青年科技英才支持计划”(NJYT-13-B09)和部分国家自然科学基金(11262013)
高鹏博(1991-),男,在读,硕士,研究方向为新型功能材料的接触力学分析;刘铁军(1978-),男,教授,博士,研究方向为新型功能材料力学行为研究
本文引用格式:高鹏博,刘铁军. 有限元分析压电半空间接触问题[J]. 新型工业化,2016,6(2):27-33.

