涪陵焦石坝区块页岩动静态弹性模量转换关系研究
熊力坤,王 升,徐烽淋,朱洪林,陈 乔,3
(1.中国石化江汉油田分公司石油工程技术研究院,湖北武汉 430035;2.中国科学院重庆绿色智能技术研究院,重庆 400714;3.中国石化地球物理重点实验室(中国石化石油物探技术研究院),江苏南京 211103)
涪陵焦石坝区块页岩动静态弹性模量转换关系研究
熊力坤1,2,王升1,徐烽淋2,朱洪林2,陈乔2,3
(1.中国石化江汉油田分公司石油工程技术研究院,湖北武汉 430035;2.中国科学院重庆绿色智能技术研究院,重庆 400714;3.中国石化地球物理重点实验室(中国石化石油物探技术研究院),江苏南京 211103)
油气开采过程中,常通过测井资料和室内试验2种方式获得岩石的力学参数,通过测井资料获得的动态力学参数与通过室内试验获得的静态力学参数相比,在资料的数量、实时性以及获取成本等方面都具有明显优势,而现有力学本构关系是基于静态力学参数建立的,因此有必要建立动静态力学参数的转换关系。鉴于此,选取层理发育完好的涪陵地区焦石坝区块下志留统龙马溪组页岩,逐一分析不同层理角度、孔隙度和声波频率对页岩弹性模量的影响,结果表明,层理角度对页岩弹性模量影响规律最强。根据试验结果,利用相关性分析法建立了层理角度与动静态弹性模量的转换关系模型,并对相同区块的页岩进行了模型验证,发现该模型预测值的平均误差小于6%,具有误差小且计算简单的特点。该研究结果可为获得层理性页岩的动静态弹性模量转换关系提供一种快速有效的方法。
层理页岩;泊松比;弹性模量;转换关系;焦石坝区块
在页岩气井钻井过程中,由于页岩地层具有天然层理特征,使井眼周围页岩所处应力环境发生急剧变化,易导致井壁页岩沿层理方向发生井壁失稳[1-2]。研究页岩层理角度对岩石力学参数的影响,对井眼稳定及水力压裂优化具有重要意义。通常情况下,采用静态法和动态法获取岩石力学参数:通过室内力学试验得到静态岩石力学参数,然后通过岩石的声波传播速度转换得到动态岩石力学参数。实际上,由于岩心取样的有限性和局限性,静态法很难避免以点代线或以点代面的现象;而动态法则克服了静态法的缺陷,在地层条件下对岩石进行测试,能较好地反映地层岩石的原始力学性质[3-4]。但是,目前关于岩石的通用理论准则是基于静态法提出来的,因此有必要对岩石动态、静态岩石力学参数之间的关系进行研究。
目前,许多国内外学者对动静态岩石力学参数之间存在的差异进行研究,形成的主要动静态弹性参数转换模型包括斯伦贝谢模型、辽河油田模型等[5]。王倩等人[6]从页岩的各向同性应力-应变关系的坐标变换出发,推导出不同层理角度页岩的弹性模量、泊松比与垂直层理、平行层理方向弹性常数的关系。目前还没有针对层理性页岩的动静态岩石力学参数转换的数学模型,大多数研究是利用统计关系得到动静态岩石力学参数的相关性。
为此,笔者拟以层理发育的涪陵地区焦石坝区块龙马溪组页岩[7-13]为研究对象,开展不同层理角度页岩的动静态力学测试,分析不同孔隙度、层理角度、不同声波频率对动静态弹性模量的影响,并提取与页岩力学参数相关性较好的因子,建立该因子与动静态弹性模量转换的数学模型,并对其进行验证。
1 试验方法
1.1岩样制备
选取涪陵焦石坝区块下志留统龙马溪组页岩岩块,按照文献[14]的要求,将所取岩块先用切割机切成便于钻孔的小岩块,然后采取液氮冷冻2 h,将冷冻后的小岩块固定在钻床上,采用液氮冷却钻头,按照层理角度(轴向应力与层理法向之间的夹角)分别为0°,15°,30°,45°,60°,75°和90°钻取岩样各10颗,钻取方案见图1。岩样长度为50.0 mm、直径为25.0 mm,上下端面的不平行度须小于0.2 mm。
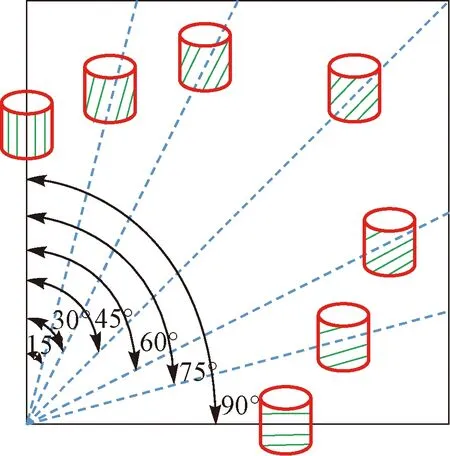
图1 岩心钻取方案Fig.1 Program for conducting coring operations
1.2试验设备
1.2.1孔隙度试验
采用HKGP-3型致密岩心气孔隙度测定仪测量岩样孔隙度。试验围压设置为3 MPa,在设定的初始压力下,气体向处于常压下装有岩心的岩心杯等温膨胀,气体扩散到岩心孔隙中,待压力稳定后,根据压力变化和已知的体积,求出有效孔隙体积和颗粒体积,然后计算岩样孔隙度:
(1)
式中:φ为孔隙度;Vp为孔隙体积,cm3;Vs为颗粒体积,cm3。
试验结果发现,页岩孔隙度变化小,变化范围为1.6%~5.3%,平均值为3.2%。
1.2.2声波试验
按层理角度(0°,15°,30°,45°,60°,75°和90°)将岩样分为7组,然后置于承压型声波换能器的探头之间,保持围压为1 MPa,完成5个测试频率(25,50,100,250和490 kHz)下的超声波测试(测试流程如图2所示),利用测试后的纵横波速结果计算得到每个岩样的动态弹性模量。
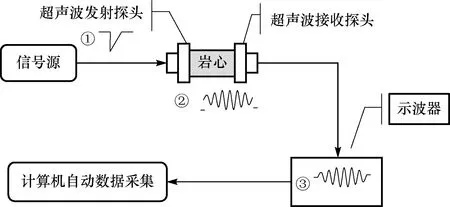
图2 超声波透射试验测试流程Fig.2 Process of conducting an ultrasonic transmission test① 激励波形(600 V负脉冲);② 在岩心中传播的超声波信号;③ 通过岩心后的透射波信号
1.2.3应力-应变试验
为了准确获取每个岩样对应的静态弹性模量,应用RTR-1000型岩心三轴试验机对完成声波测试后的岩样进行三轴测试。按竖向位移控制试验过程,速率为0.1 mm/min,围压保持为13.5 MPa,加载直到试样破坏。完成试验后,根据得到的应力-应变曲线计算岩样对应的静态弹性模量。
2 动静态弹性模量相关性分析
声波试验发现,不同层理角度、孔隙度和测试频率(声波探头频率)下岩样的纵横波速不同,这表明层理角度、孔隙度及测试频率对动态弹性模量有影响。因此,利用声波测试结果来探究不同层理角度、频率、孔隙度对动态弹性模量的影响规律。试验结果如图3所示。

图3 不同频率、层理角度条件下的动态弹性模量Fig.3 Dynamic elastic modulus under different acoustic frequencies and bedding angles
从图3可以看出:层理角度和频率对动态弹性模量均有影响,其中在相同层理角度条件下,岩样的动态弹性模量变化范围小,整体随着频率的增加有减少的趋势;相同频率下,岩样的层理角度对动态弹性模量影响较大,动态弹性模量随着层理角度的增加而减小,其中层理角度为0°的动态弹性模量最大,平均值为45 GPa,层理角度为90°的动态弹性模量最小,平均值为32 GPa。分析认为,这是由于层理面处的胶结物较多,黏土矿物产状相对混乱,层理面的存在增加了声波衰减,减小了波速。当层理角度为0°时,页岩的层理与声波角度平行,声波衰减最弱,对声波速度影响小;而当层理角度为90°时,声波需要穿过最多的层理层,因而衰减最大,对声波速度影响大。故而,层理角度越大,岩样动态弹性模量越小。
图4为不同孔隙度的页岩在不同声波探头频率(纵波频率分别为25,50,100,250和490 kHz)条件下试验得到的动态弹性模量。
由图4可知,岩样孔隙度对其动态弹性模量的影响规律复杂,大致呈现为先增大后减小然后再增大的规律。在相同孔隙度下,不同声波频率对动态弹性模量影响的规律性不强,声波频率为250 kHz时岩样的动态弹性模量最小,而声波频率为50 kHz时岩样的动态弹性模量最大。
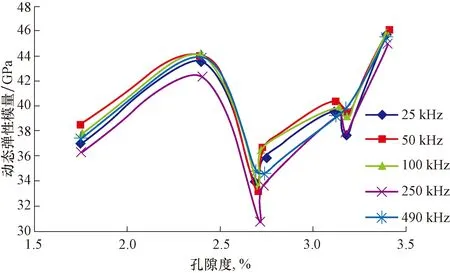
图4 不同孔隙度和探头频率下的动态弹性模量Fig.4 Dynamic elastic modulus under different porosities and frequencies
根据三轴试验得到的应力-应变曲线计算岩样的静态弹性模量,层理角度、孔隙度与静态弹性模量的关系如图5、图6所示。
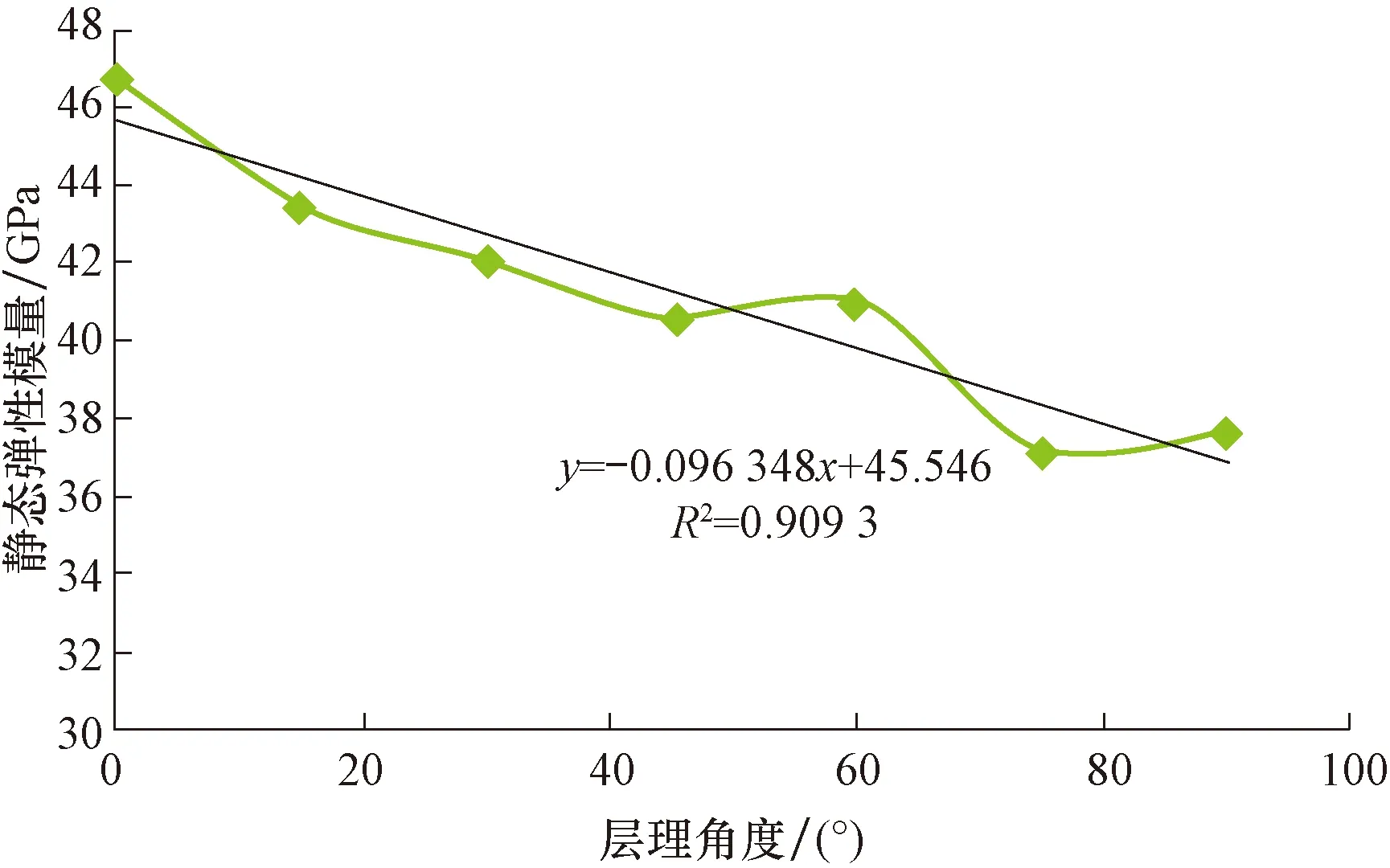
图5 层理角度与静态弹性模量的关系Fig.5 Correlation between static elastic modulus and bedding angle
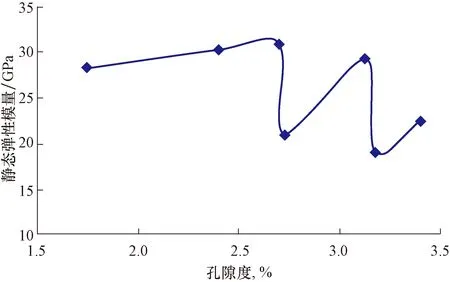
图6 孔隙度与静态弹性模量的关系Fig.6 Correlation between static elastic modulus and porosity
从图5可以看出,静态弹性模量随层理角度的增加呈线性递减的趋势,其中在层理角度为60°时,静态弹性模量略微增大。从图6可以看出,页岩岩样孔隙度变化范围小,静态弹性模量与孔隙度之间没有呈现出明显的规律性。
3 模型的建立与验证
3.1模型建立
由前文分析可知,动静态弹性模量与页岩层理角度的关系曲线均呈现出较强的规律性,而孔隙度、声波频率与动静态弹性模量的关系曲线的规律性不强。实际油气生产过程中,页岩高度发育的层理特征,是影响油气井工程参数的重要因素。综合考虑相关性分析结果与工程实践的应用,以层理角度为研究对象建立动静态参数转换关系。因此,选取孔隙度基本相同的岩样,在同一声波频率下分析7个不同层理角度下的动静态弹性模量,建立层理角度与动静态力学参数之间的关系,其试验数据与结果见表1。
表1不同层理角度岩样的动静态弹性模量
Table 1Dynamic and static elastic modulus of samples with different bedding angles
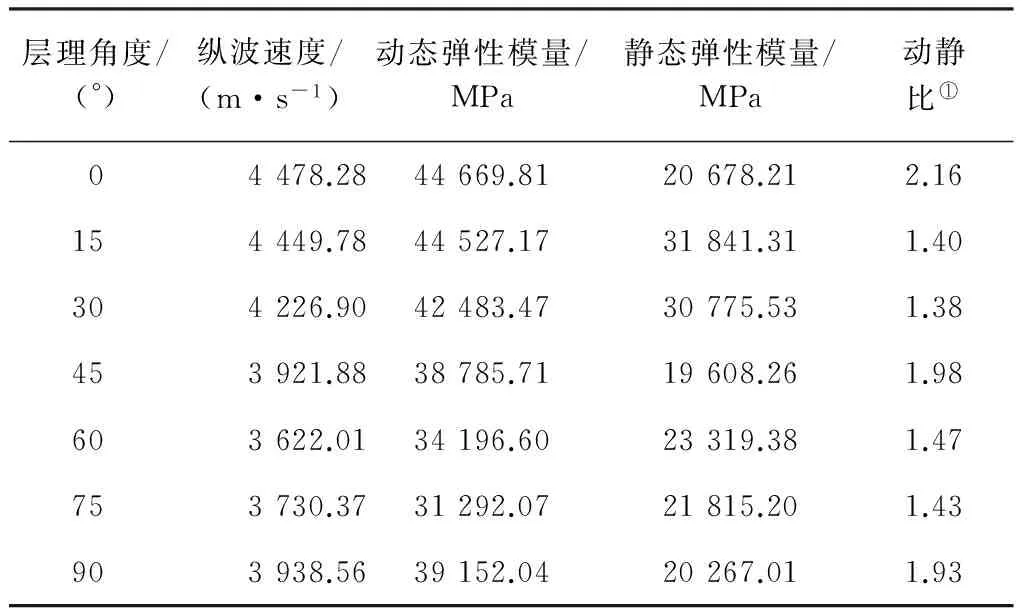
层理角度/(°)纵波速度/(m·s-1)动态弹性模量/MPa静态弹性模量/MPa动静比①04478.2844669.8120678.212.16154449.7844527.1731841.311.40304226.9042483.4730775.531.38453921.8838785.7119608.261.98603622.0134196.6023319.381.47753730.3731292.0721815.201.43903938.5639152.0420267.011.93
注:1)为动态弹性模量与静态弹性模量的比值。
从表1可以看出,页岩层理角度不同,动态弹性模量与静态弹性模量的比值(简称动静比)不同,当层理角度为0°,45°和90°时,动静比相对较大;层理角度为15°,30°,60°和75°时,动静比相对较小。
根据表1计算不同层理角度下的动静态参数转换系数,结果如图7所示。
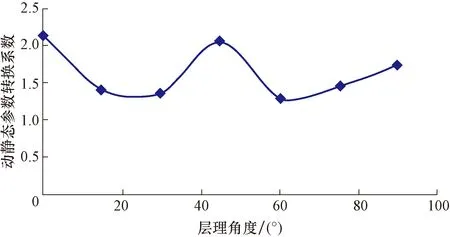
图7 不同层理角度的动静态参数转换系数Fig.7 Conversion factors for dynamic and static elastic modulus under different bedding angles
图7表明,岩石的动静态参数转换系数与层理角度的关系曲线大体为三角函数曲线。在此基础上,结合表1的试验数据研究得出层理角度与动静态弹性模量之间的转换关系模型:
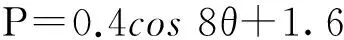
(2)
式中:P为动静比;θ为层理角度,(°)。
3.2模型验证
为了验证模型的可靠性,选取另外7组不同层理角度的页岩岩心(取自焦页7井3 446.23~3 582.84 m井段)进行验证,按照上述试验流程分别测定动静态弹性模量,并利用上述模型预测岩样的动静态弹性模量。分析实际的动静比与模型的预测动静比及误差,结果见表2。
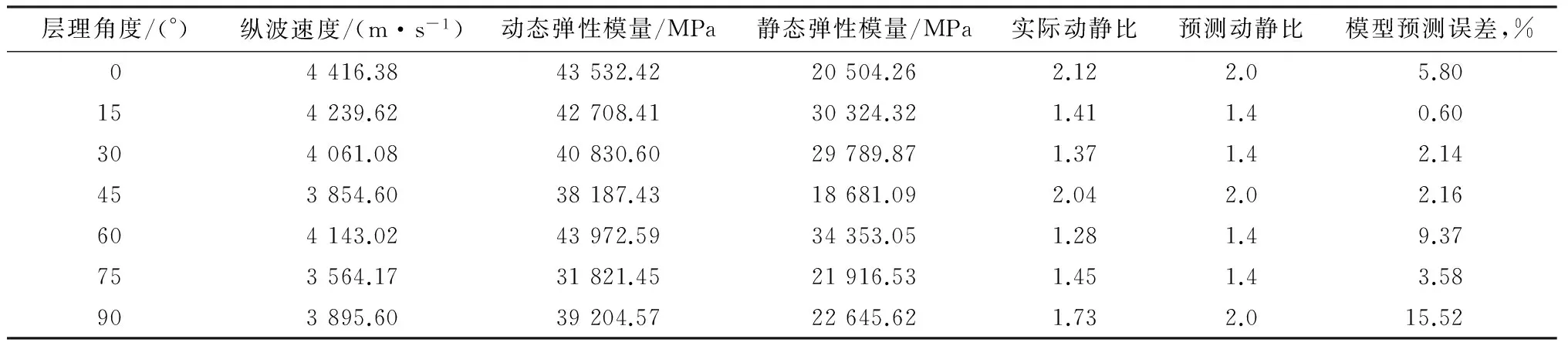
表2 模型验证结果
由表2可知,7组岩心的试验结果中,最大预测误差为15.52%,最小预测误差为0.60%,平均误差为5.59%,可见该模型不仅计算简便而且较为准确,对涪陵焦石坝区块层理页岩具有一定的适用性。
4 结 论
1) 分析不同孔隙度、声波频率、层理角度对页岩弹性模量的影响规律发现,层理性页岩的动静态力学参数对层理角度的敏感性最强。
2) 建立了针对涪陵地区焦石坝区块层理性页岩的动静态弹性模量转换的预测模型。验证结果表明,该模型具有误差小且计算简便的特点,有较好的适用性。
3) 涪陵地区焦石坝区块下志留统龙马溪组页岩储层,由于存在构造变化复杂的特点,不同区块差异较大,利用本文方法能更加深入地认识不同区块层理与岩石力学参数的相互关系,这对于未来压裂工艺参数的优化具有指导意义。
[1]王世谦.中国页岩气勘探评价若干问题评述[J].天然气工业,2013,33(12):13-29.
WANG Shiqian.Shale gas exploration and appraisal in China:problems and discussion[J].Natural Gas Industry,2013,33(12):13-29.
[2]陈勉,葛洪魁,赵金洲,等.页岩油气高效开发的关键基础理论与挑战[J].石油钻探技术,2015,43(5):7-14.
CHEN Mian,GE Hongkui,ZHAO Jinzhou,et al.The key fundamentals for the efficient exploitation of shale oil and gas and its related challenges[J].Petroleum Drilling Techniques,2015,43(5):7-14.
[3]王红岩,刘玉章,董大忠,等.中国南方海相页岩气高效开发的科学问题[J].石油勘探与开发,2013,40(5):574-579.
WANG Hongyan,LIU Yuzhang,DONG Dazhong,et al.Scientific issues on effective development of marine shale gas in southern China[J].Petroleum Exploration and Development,2013,40(5):574-579.
[4]贾长贵,陈军海,郭印同,等.层状页岩力学特性及其破坏模式研究[J].岩土力学,2013,34(增刊2):57-61.
JIA Changgui,CHEN Junhai,GUO Yintong,et al.Research on mechanical behaviors and failure modes of layer shale[J].Rock and Soil Mechanics,2013,34(supplement 2):57-61.
[5]单钰铭,刘维国.地层条件下岩石动静力学参数的实验研究[J].成都理工学院学报,2000,27(3):249-254.
SHAN Yuming,LIU Weiguo.Experimental study on dynamic and static pa-rameter of rocks under formation conditions[J].Journal of Chengdu College of Geology,2000,27(3):249-254.
[6]王倩,王鹏,项德贵,等.页岩力学参数各向异性研究[J].天然气工业,2012,32(12):62-65.
WANG Qian,WANG Peng,XIANG Degui,et al.Study on the anisotropy of shale mechanical parameters[J].Natural Gas Industry,2012,32(12):62-65.
[7]杨恒林,申瑞臣,付利.含气页岩组分构成与岩石力学特性[J].
石油钻探技术,2013,41(5):31-35.
YANG Henglin,SHEN Ruichen,FU Li.Composition and mechanical properties of gas shale[J].Petroleum Drilling Techniques,2013,41(5):31-35.
[8]韩双彪,张金川,邢雅文,等.渝东南下志留统龙马溪组页岩气聚集条件与资源潜力[J].煤炭学报,2013,38(增刊1):168-173.
HAN Shuangbiao,ZHANG Jinchuan,XING Yawen,et al.Shale gas accumulation conditions and resource potential of the Lower Silurian Longmaxi Formation in Southeast Chongqing[J].Journal of China Coal Society,2013,38(supplement 1):168-173.
[9]王森,刘洪,陈乔,等.渝东南下志留统龙马溪组页岩理化性能实验[J].石油学报,2014,35(2):245-252.
WANG Sen,LIU Hong,CHEN Qiao,et al.Physical and chemical properties experiment on shale in Longmaxi Formation of Lower Silurian,Southeast Chongqing[J].Acta Petrolei Sinica,2014,35(2):245-252.
[10]王玉满,董大忠,李建忠,等.川南下志留统龙马溪组页岩气储层特征[J].石油学报,2012,33(4):551-561.
WANG Yuman,DONG Dazhong,LI Jianzhong,et al.Reservoir characteristics of shale gas in Longmaxi Formation of the Lower Silurian,southern Sichuan[J].Acta Petrolei Sinica,2012,33(4):551-561.
[11]刘树根,马文辛,JANSA L,等.四川盆地东部地区下志留统龙马溪组页岩储层特征[J].岩石学报,2011,27(8):2239-2252.
LIU Shugen,MA Wenxin,JANSA L,et al.Characteristics of the shale gas reservoir rocks in the Lower Silurian Longmaxi Formation,east Sichuan Basin,China[J].Acta Petrologica Sinica,2011,27(8):2239-2252.
[12]曾祥亮,刘树根,黄文明,等.四川盆地志留系龙马溪组页岩与美国Fort Worth盆地石炭系Barnett组页岩地质特征对比[J].地质通报,2011,30(2/3):372-384.
ZENG Xiangliang,LIU Shugen,HUANG Wenming,et al.Comparison of Silurian Longmaxi Formation shale of Sichuan Basin in China and Carboniferous Barnett Formation shale of Fort Worth Basin in United States[J].Geological Bulletin of China,2011,30(2/3):372-384.
[13]邓康龄.四川盆地形成演化与油气勘探领域[J].天然气工业,1992,12(5):7-12.
DENG Kangling.Formation and evolution of Sichuan Basin and domains for oil and gas exploration[J].Natural Gas Industry,1992,12(5):7-12.
[14]GB/T 50266—2013工程岩体试验方法标准[S].
GB/T 50266—2013Standard test method for rock engineering[S].
[编辑令文学]
Dynamic and Static Elastic Modulus Conversion for Shale in the Jiaoshiba Block,Fuling Area
XIONG Likun1,2,WANG Sheng1,XU Fenglin2,ZHU Honglin2,CHEN Qiao2,3
(1.ResearchInstituteofPetroleumEngineeringTechnology,SinopecJianghanOilfieldCompany,Wuhan,Hubei,430035,China; 2.ChongqingInstituteofGreenandIntelligentTechnology,ChineseAcademyofScience,Chongqing,400714,China; 3.SinopecKeyLaboratoryofGeophysics(SinopecGeophysicalResearchInstitute),Nanjing,Jiangsu,211103,China)
Mechanical parameters of rocks can be obtained in two ways:well logging and laboratory experiments.The determination of dynamic mechanical parameters from well logging is much superior to those obtained through lab tests in terms of the data quantity,real-time performance and acquisition costs.Existing mechanical constitutive relationships are based on static parameters,so it is necessary to define the conversion between dynamic parameters and static ones.For this purpose,shale with intact bedding structures in the Lower Silurian Longmaxi Formation of Jiaoshiba Block,Fuling Area,was used to determine the impact of bedding angles,porosities and acoustic frequencies on the elastic modulus of shale.Research results showed that the bedding angles had the highest impact on the elastic modulus of shale.Accordingly,the conversion model between dynamic and static elastic modulus was established by using the correlation analysis method.Samples of shale taken from the same block were used to verify the results of the model.It was determined that the model had an average prediction error of less than 6%.The research results may provide an effective way to calculate dynamic and static elastic moduli for interbedded shales.
interbedded shale; Poisson’s ratio; elastic modulus; conversion relation; Jiaoshiba Block
2015-10-12;改回日期:2016-06-30。
熊力坤(1984—),男,四川成都人,2008年毕业于西南石油大学石油工程专业,2011年获西南石油大学油气田开发工程专业硕士学位,工程师,主要从事储层改造方面的研究工作。E-mail:xlk2080@163.com。
重庆市基础与前沿研究计划项目“基于页岩剪切裂纹形成、扩展机制的水平井井壁崩落评估模型研究与应用示范”(编号:cstc2015jcyjBX0120)、中国石化地球物理重点实验室开放基金“渝东南下志留统龙马溪组页岩超声波特性数值模拟研究”(编号:33550006-15-FW2099-0018)资助。
◀钻井完井▶doi:10.11911/syztjs.201605007
TE312
A
1001-0890(2016)05-0040-05

