油藏模拟历史拟合中Levenberg-Marquardt算法的改进
张鲜,AWOTUNDE A A
(1. Abu Dhabi Marine Operating Company; 2. King Fahd University of Petroleum & Minerals)
油藏模拟历史拟合中Levenberg-Marquardt算法的改进
张鲜1,AWOTUNDE A A2
(1. Abu Dhabi Marine Operating Company; 2. King Fahd University of Petroleum & Minerals)
为了更高效地利用历史拟合方法估算油藏参数,提出采用差分进化(DE)方法估算最佳阻尼因子,改进标准的Levenberg-Marquardt(LM)算法,并通过算例分析验证改进后的算法。标准的LM算法中采用试错法估算阻尼因子,对于大型反演问题可靠性较差,采用DE方法可以有效解决此问题,且不需要使用线搜索去寻找合理步长。将改进后的算法应用于两个不同大小油藏模型的历史拟合中,并与其他算法进行对比,结果表明:运用DE方法使LM算法的收敛速度加快、残差减小,不仅适用于小型、中型反演问题,更适用于大型反演问题;在预设LM算法迭代终止标准的情况下,使用改进后的算法可以减少迭代次数、大幅节省总计算时间,从而提高历史拟合效率。图10表2参15
油藏数值模拟;历史拟合;Levenberg-Marquardt算法;差分进化;线搜索
0 引言
为了有效地管理油气藏,需要对油气藏的流体流动特性进行可靠预测,其中1个难题在于如何估算控制流体流动的油藏参数值。目前还没有兼顾计算效率和计算精度的油藏参数估算方法:有些算法用于小型或中型问题时比较有效,但用于大型问题时计算效率较低;有些算法用于大型问题时计算效率较高,但计算精度较差。利用历史拟合估算油藏参数的方法已使用多年[1-6],但历史拟合非常费时,尤其是需要估计的参数很多时。Levenberg-Marquardt(LM)算法是其中1种常用的基于梯度进行参数估算的反演方法[7]。该算法用于小型和中型反演问题时效率很高,但当问题的维数很大时计算量非常大。这是因为LM算法需要在每次迭代时计算敏感度矩阵,油藏规模越大越需要计算敏感度矩阵。而正因为LM算法保留了敏感度矩阵的重要信息,其计算结果优于其他大多数同类算法。
LM算法是1种改进的Gauss-Newton方法[7-8],它将阻尼因子λ添加到Gauss-Newton Hessian矩阵的对角元素中。这个阻尼因子为正值,其作用是在矩阵趋于奇异时稳定矩阵。选择合理的λ值既能够加快算法的收敛速度,又不必采用线搜索(LSCH)去寻找适当的步长值[8]。然而,确定最佳阻尼因子的过程十分困难,尤其是对于大型反演问题。常用方法是采用试错法反复试验、逐步逼近,但有时会出现收敛性变差或者不收敛的问题。
本文提出采用1种全局最优化算法——差分进化(DE)算法来估算LM算法每次迭代中的阻尼因子λ,通过减少迭代次数来减少LM算法的总计算时间。利用两个油藏模型对提出的方法进行验证,并与目前常用的方法进行对比。
1 理论基础
根据钻井数据直接获得的油藏参数信息很少,而利用现有生产数据进行历史拟合可间接估算渗透率、孔隙度等油藏物性[2,9]。一般说来,历史拟合首先要定义目标函数,最常用的目标函数是实测数据与计算数据之间误差的欧几里得范数:
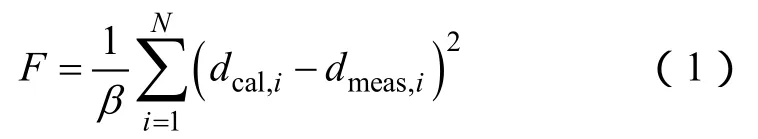
此外,还要确定需要估算的油藏模型参数以及选择合适的最优化算法。历史拟合使用的最优化算法一般分为两类:局部寻优和全局寻优。全局最优化算法非常耗费计算资源,因此往往局限于小型和中型反演问题,而局部最优化算法在处理大型问题时效率更高。大多数局部最优化算法利用目标函数的梯度确定可能的搜索方向,被称为基于梯度的算法。基于梯度的算法采用根据敏感度系数计算的精确或近似Hessian矩阵,比其他不使用Hessian矩阵的算法更快收敛。对于大型油藏参数反演问题,基于梯度的算法是最常用的最优化算法。这些算法中最常用的包括拟Newton算法、Gauss-Newton算法和LM算法。本文主要研究如何改进LM算法。
1.1 Levenberg-Marquardt算法
LM算法是一种基于梯度的算法,它采用敏感度矩阵计算Hessian矩阵。LM算法通过迭代过程实现,在每次迭代中,都要计算一个近似的牛顿方向sj:

(2)式中,Hessian矩阵计算方法如下:

(3)式中,敏感度矩阵S由下式给定:

(3)式中,对称的半正定矩阵STS即所谓的Gauss-Newton Hessian矩阵,它可能含有零值本征值(奇异),也可能接近奇异,或者出现严重病态。加入1个对角矩阵λI有助于稳定Hessian矩阵,确保该矩阵保持正定。λ值的大小会影响迭代次数,从而影响算法的收敛速度。如果λ值太小,Hessian矩阵仍将趋于奇异或者严重病态;如果λ值太大,迭代步长会非常小,这不利于计算的快速收敛。
根据(2)式计算出近似的牛顿方向后,后续迭代用下式计算:

(5)式中,υ为迭代步长,它决定了沿计算方向的迭代次数。只有当(3)式中所用λ值不合适时,才有必要估算υ。如果采用了合理的λ值,那么根据(2)式计算的牛顿方向就会保证迭代次数也合理,因此没有必要额外再去计算υ[8]。α为模型参数矢量,本文估算的模型参数为渗透率对数lnK。
1.2 线搜索
线搜索(LSCH)经常用于寻找适用步长υ。本文使用的线搜索算法满足强Wolfe条件[7,10],该算法的目的是要找到满足充分下降条件的步长,即:
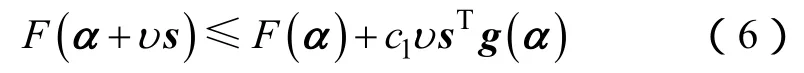
曲率条件为:
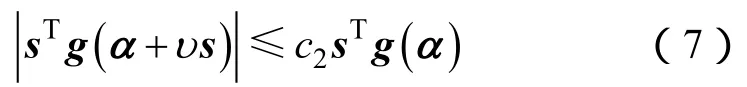
(6)式、(7)式中,0<c1<c2<1,c1和c2的标准值参见文献[7]。
1.3 差分进化
本文采用差分进化(DE)算法估计LM算法中的阻尼因子λ。DE算法通过迭代方式改进目标函数的候选解,从而求解最优化问题。本文中目标函数如(1)式所示。在基本DE算法中,根据未知变量上、下限之间的均匀分布随机生成候选解的初始种群:
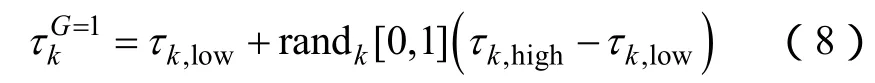
种群大小(候选解的数量)由下式[11]确定:
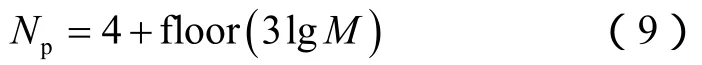
(9)式最初是用于进化策略(ES)算法,但是后来Awotunde[12]发现(9)式对DE算法同样适用,计算的种群大小更合适。
确定该种群中最佳候选解的方法是评价每个候选解目标函数值的适应度。再将这个候选解作为从当前这一代种群中所能找到的最优解,并将其存储在外部。如果之后发现更好的解,就对这个外部存储的最优解进行更新。然后利用如下任一公式,对每一个候选解进行突变运算:
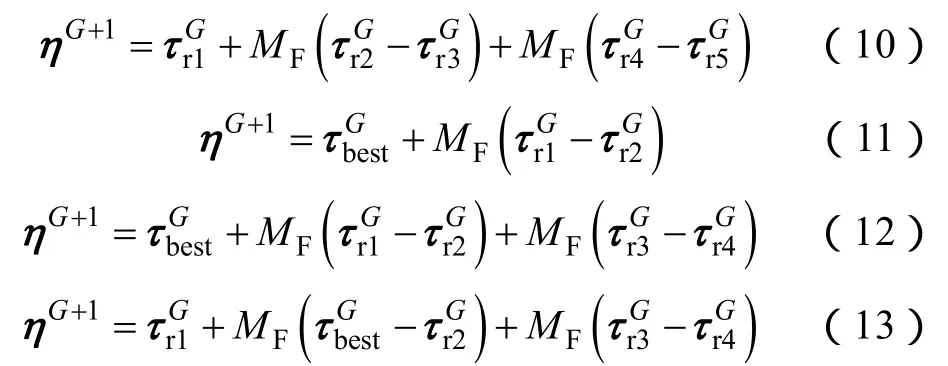
2 Levenberg-Marquardt算法的改进
将使用线搜索的标准Levenberg-Marquardt算法称为LM+LSCH算法,它采用试错法估算阻尼因子λ,求解近似牛顿方向,再采用线搜索算法寻找合理步长(每次LM迭代中嵌入另一个迭代过程)。本文用DE算法取代试错法,不使用线搜索,直接设置步长,将这种算法称为LM+DE算法。由于不需要寻找合理步长,并且可以在每次DE迭代中并行估算最优候选解,从而可以节省大量时间。此外,因为只有1个未知量λ,故将DE算法中的种群大小设置为4。
本文提出的LM+DE算法概述如下:
①设置未知模型参数矢量α的初始估计值,设置λ的上、下限;
②使用当前的α值计算敏感度矩阵S、对称半正定矩阵STS以及梯度g;
③运行DE算法,以确定预置搜索范围内的λ值,再根据(3)式计算Hessian矩阵H;
④根据(2)式求解近似牛顿方向s,将步长υ设为1,根据(5)式生成新的α估计值;
⑤重复步骤②到④,直到满足LM算法预设的终止条件时结束。
DE算法中,每次函数求值都必须针对不同的λ值求解(2)式,对每个λ值都必须求得新的α估计值,并且必须进行正演模拟以确定对应每个λ值的残差,从而根据不同残差来确定最好的λ估计值。因此,DE算法中两个最费时的运算就是求解(2)式和进行油藏正演模拟。DE算法中包含几次函数求值,这两个运算就必须执行几次。(2)式问题的大小就是α中未知量的个数,通常与模拟系统中的网格数量有关,如果使用了模型降阶方法,就与阈值的设定有关[13-14]。正演模拟中问题的大小既与网格数量有关,又与模型中相数或组分数有关。求解(2)式的计算时间远远低于进行1次正演模拟的时间,因此可以忽略。
本文提出LM+DE算法以取代LM+LSCH算法,这两个算法中都包含标准LM算法的计算步骤,是LM算法的不同版本。它们之间的区别在于如何改进每次LM迭代中的牛顿步(大小和方向):LM+DE算法试图直接找到1个合理的牛顿步,而LM+LSCH算法首先找到1个大致的牛顿方向,再计算沿这个方向的合理步长。两种算法的实际差别在于,LM+DE算法使用DE估算合理的λ值,而LM+LSCH算法采用LSCH估算合理的υ值。两种算法计算量的差别取决于求解问题的类型和大小。在每次LM迭代中,如果DE进行5次迭代,那么它的函数求值就要执行20次。这就意味着除了标准LM算法的计算步骤(如计算敏感度矩阵、梯度等)以外,在每次迭代中还要执行20次正演模拟和求解(2)式。LM+LSCH算法中的LSCH是1个迭代过程,最多执行5次迭代,这5次迭代必须依次执行,但是如果试错法得到的λ值足够好,迭代次数可能少于5次。每次迭代都包括运行1次正演模拟和计算梯度。为了减少LSCH迭代期间计算梯度的时间,本文使用了1个伴随方程。这样,每次LSCH迭代就需要运行1次正演模拟和1次伴随模拟。因为伴随模拟与正演模拟计算量大致相当,最多5次迭代就差不多相当于最多10次正演模拟。因此,DE的计算量多于LSCH。但是,由于DE各个候选解的迭代可以并行,预计对于大型问题LM+DE算法比LM+LSCH算法耗时更少。此外,采用LM+DE算法时,DE消除了λ值估计的不确定性,只要提供合理的λ值上下限,就能很好地搜索。而试错法首次迭代中λ值的不当选择(过大或过小)可能导致LM计算的收敛很慢或(2)式中矩阵趋于奇异。
大多数情况下,DE算法会产生较好的λ估计值,并且已经确定如果λ值合理,就没有必要进行线搜索。但是,当采用不同的随机数设置进行计算时,DE之类的全局最优化方法有可能产生不同的结果。因此,不能保证DE算法总能得到足够好的λ值。为了评估LM+DE算法的可靠性,将LM+DE+LSCH作为一个新的算法进行计算,然后将运行情况与LM+DE算法进行对比。显然,由于LM+DE+LSCH算法除了采用DE算法估计λ值,还使用线搜索确定υ值,比LM+LSCH算法和LM+DE算法更费时。
3 算法验证
设计了两个不同尺寸(16×16和64×64)的油藏模型,来验证LM+DE算法的性能。通过拟合压力和含水率数据估算渗透率对数。研究了3种不同数据拟合情况的算例:算例1只拟合压力数据;算例2只拟合含水率数据;算例3同时拟合压力和含水率数据。通过1个已知的渗透率场模拟生产数据,然后加入高斯白噪,得到的数据作为实测数据。具体来说,实测数据计算公式[15]为:
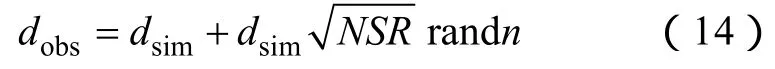
压力和含水率数据的信噪比NSR分别设为10-6和10-5。计算中流体和储集层性质为:标准条件下的原油密度642.7 kg/m3(40 lbm/ft3),标准条件下的水密度1 000 kg/m3(62.238 lbm/ft3),原油等温压缩系数1.7× 10-4MPa-1(1.2×10-6psi-1),水等温压缩系数7.3×10-5MPa-1(5×10-7psi-1),初始油藏压力34.48 MPa(5 000 psi),初始含水饱和度1×10-6,初始孔隙度25%,井半径76.2 mm(0.25 ft),表皮系数为零。
对两个油藏模型都分别使用了3种算法,即LM+DE、LM+LSCH和LM+DE+LSCH,通过拟合实测数据来估算油藏渗透率分布。对于每个模型,LM算法的迭代次数为10次。在LM+LSCH和LM+DE+LSCH算法中,设置LSCH最多执行5次迭代。在LM+DE和LM+DE+LSCH算法中,DE的候选解种群中设置4个候选解,迭代次数设为5次。这样,不论何时调用DE估算λ值,都会调用20次正演模拟程序。但是,由于每次DE迭代时4个候选解的迭代是并行的,因此20次函数调用所需的时间与5次函数调用的时间大致相等,可以节省大量时间。
LM+LSCH算法中采用试错法估算λ值。该方法首先设置一个初始估计值,然后在每次LM迭代中,根据误差是否减小来决定对估计值除以还是乘以1个因子,常用的因子值有4和10。本文中这两个因子值都使用了,将使用因子4的LM+LSCH标记为LM1+LSCH,使用因子10的LM+LSCH标记为LM2+LSCH。
为了客观对比,所有算法都使用配置相同的计算机设备(64 GB内存、Core i7 4960X Intel处理器),并在相同的计算条件下运行。
3.1 油藏模型1
油藏模型1大小为16×16,图1显示其渗透率场不均匀,包含3口生产井和2口注水井,各井同时投入运行。需要拟合的数据是所有井的压力数据和生产井的含水率数据。共8组数据,包括生产井的3组井底压力数据和3组含水率数据以及注水井的2组井底压力数据。每组数据有256个数据点,总数据点为2 048个。
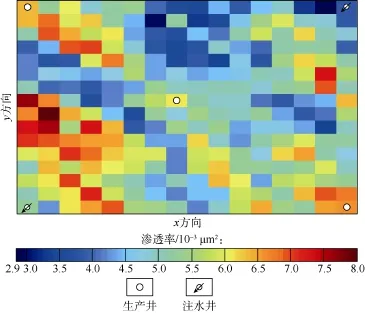
图1 油藏模型1的真实渗透率场和井位
图2为油藏模型1各算例误差范数值随迭代次数的衰减曲线,可以看出:在收敛速度方面,LM+DE算法明显优于LM1+LSCH和LM2+LSCH;LM+DE和LM+DE+LSCH算法的残差衰减曲线几乎是重合的。这表明用DE算法替代试错法来估算λ值,不使用线搜索,计算更高效。
表1详细列出了LM1+LSCH、LM2+LSCH、LM+DE和LM+DE+LSCH等4种算法在油藏模型1的3种算例中的执行情况。由表1可知:对于油藏模型1这样的小型问题,在都进行10次LM迭代的情况下,LM1+LSCH和LM2+LSCH的计算时间均少于LM+DE的计算时间;LM+DE+LSCH的计算时间最多,这是因为它在每次LM迭代中都执行了DE和LSCH这两种运算,而与LM+DE相比,收敛速度并无明显改善(见图2),因此没有必要再使用LSCH。
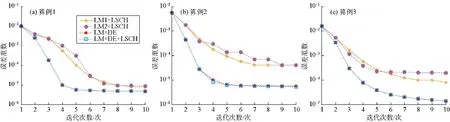
图2 油藏模型1各算例的残差衰减曲线
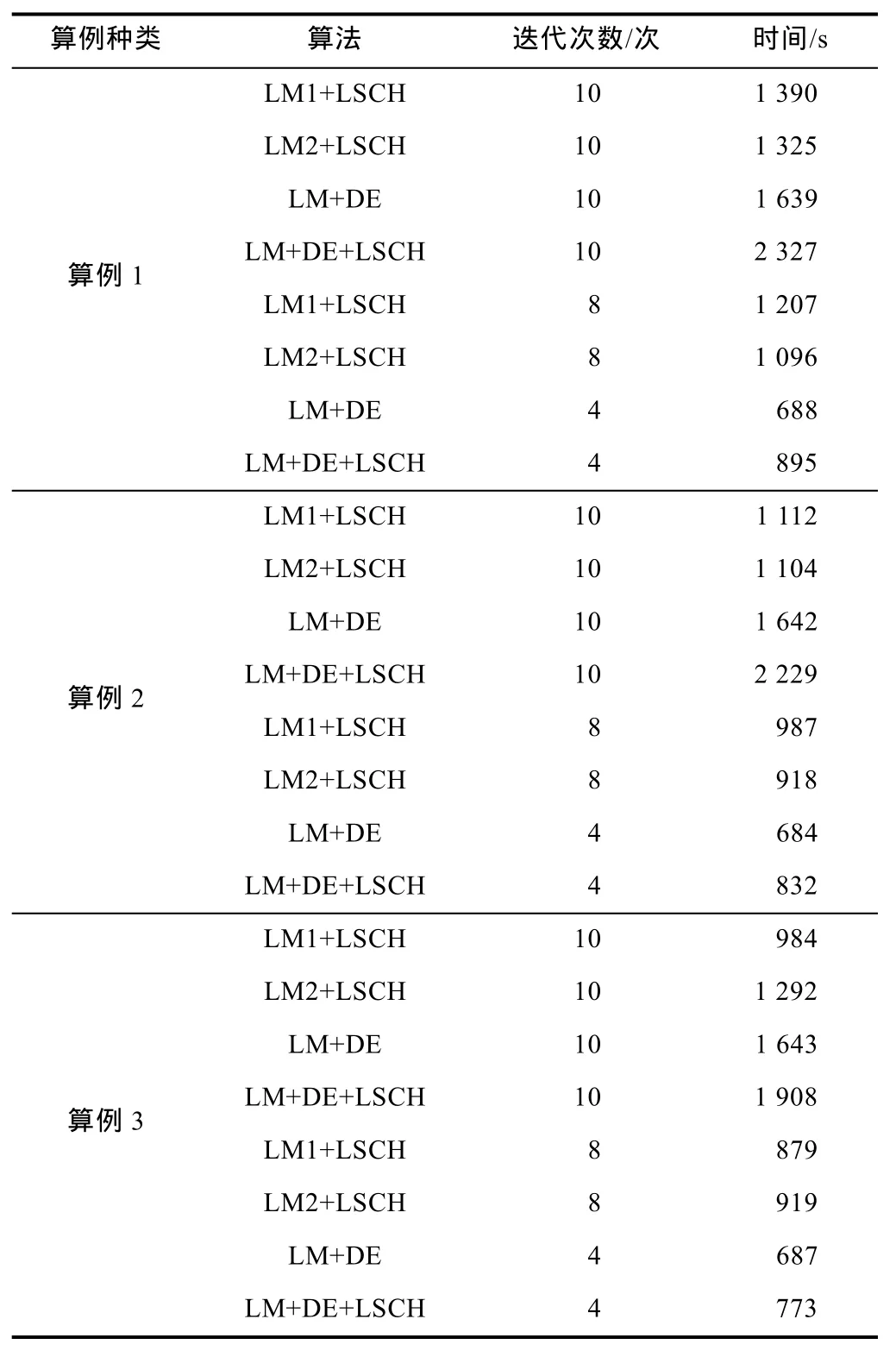
表1 油藏模型1各算法不同迭代次数对应的计算时间
由于LM+DE收敛很快,预先设置1个残差值作为LM迭代的终止标准,在第4次迭代时终止LM+DE和LM+DE+LSCH,在第8次迭代时终止LM1+LSCH和LM2+LSCH,然后对比各算法的计算时间(见表1)。可以看出,在预设终止标准的情况下,LM+DE的计算时间比LM+LSCH和LM+DE+LSCH的计算时间都少;与LM1+LSCH和LM2+LSCH相比,LM+DE可节省计算时间192~519 s。这是因为,每次LM迭代中有相当一部分时间用于计算敏感度矩阵,而LM+DE算法减少了迭代次数,就使总计算时间显著减少。
图3、图4为采用不同算法得到的油藏模型1的生产数据拟合结果,可以看出:所有算法的计算结果与实测数据都很匹配,LM+DE算法在处理小型历史拟合问题时是可靠的。
图5为采用不同算法估算的油藏模型1渗透率场,可以看出,由于缺少足够的信息去完全求解模型参数,采用各算法估算的渗透率场与真实渗透率场都不相同。
3.2 油藏模型2
油藏模型2大小为64×64,其渗透率场如图6所示,包含24口生产井和16口注水井,各井同时投入运行。需要拟合的数据是所有井的压力数据和生产井的含水率数据,因此共64组数据,每组数据有140个数据点,总数据点为8 960个。
首先,设置最多执行10次LM迭代,在这种情况下,LM+DE与LM+LSCH算法的计算时间基本相同(见表2),这与油藏模型1中的情况不同。这是因为在油藏模型2这样的大型问题中,LSCH需要更多次迭代才能找到合理步长,并且在LSCH的每次迭代中,计算梯度的时间会随着问题维数的增长而增加,因此需要更多计算时间。
图7为油藏模型2各算例误差范数值随迭代次数的衰减曲线,可以看出:LM+DE和LM+DE+LSCH的收敛速度比其他算法快,残差也比其他算法小;对于大部分LM迭代,LM+DE和LM+DE+LSCH的误差范数基本相同,这表明当使用DE估算λ值时,就不太需要或不需要进行LSCH;在算例2中LM+DE和LM+DE+LSCH从第7步到第10步迭代的差异(见图7b),可以归因为DE不能保证每次LM迭代都能找到最合适的λ值,在这种情况下LSCH能够得到更小的残差。
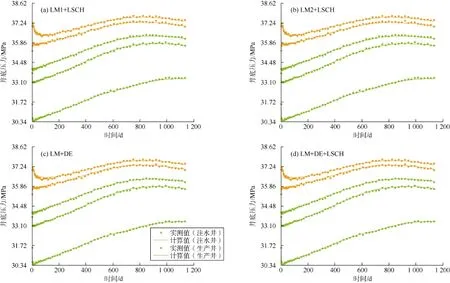
图3 油藏模型1基于不同算法得到的5口井的压力数据拟合结果
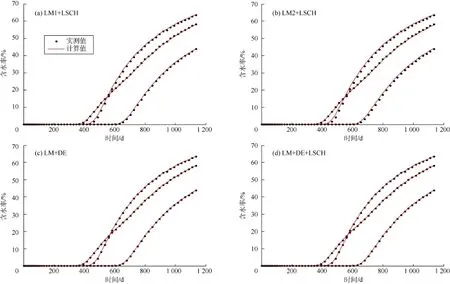
图4 油藏模型1基于不同算法得到的3口井的含水率数据拟合结果
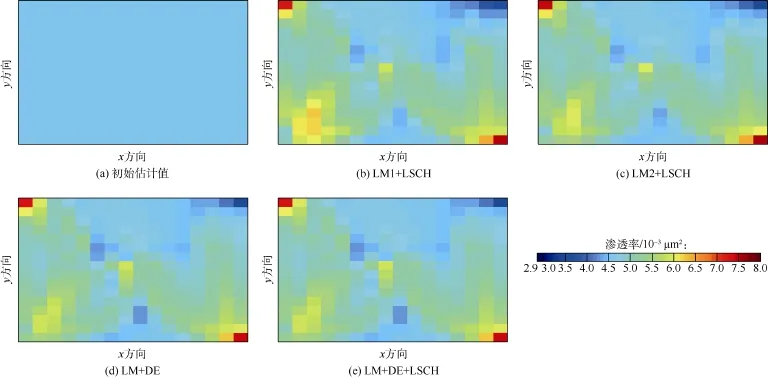
图5 油藏模型1基于不同算法估算的渗透率场
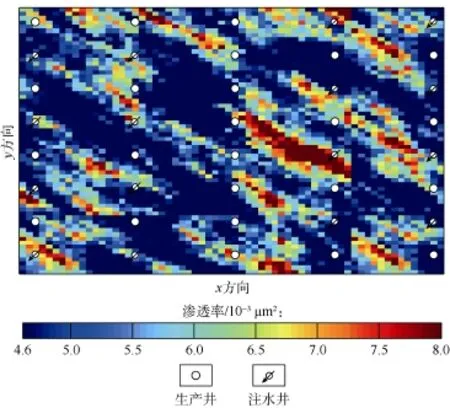
图6 油藏模型2的真实渗透率场和井位
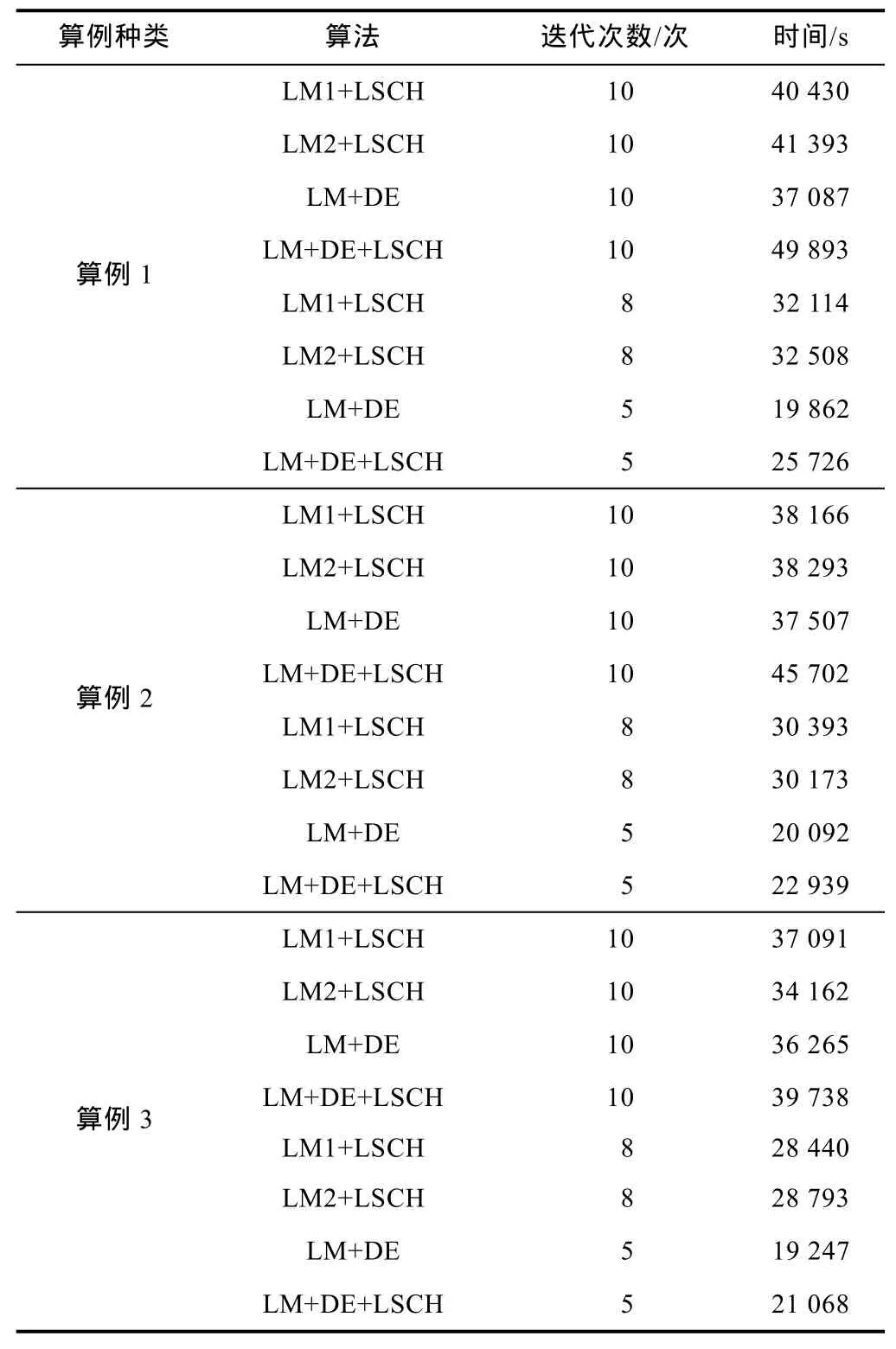
表2 油藏模型2各算法不同迭代次数对应的计算时间
同理,预先设置1个残差值作为LM迭代的终止标准,在第5次迭代时终止LM+DE和LM+DE+LSCH,在第8次迭代时终止LM1+LSCH和LM2+LSCH,然后对比各算法的计算时间(见表2)。可以看出,在预设终止标准的情况下,与LM1+LSCH和LM2+LSCH相比,LM+DE计算时间大幅减少,可节省计算时间9 193~12 646 s,说明对于大型问题LM+DE也比LM+LSCH效率更高。
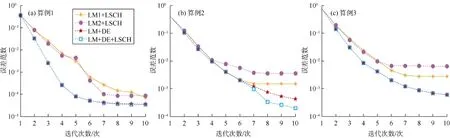
图7 油藏模型2各算例的残差衰减曲线
图8、图9为采用不同算法得到的油藏模型2的压力、含水率数据拟合结果,可以看出:所有算法的计算结果与实测数据都很匹配,LM+DE算法在处理大型历史拟合问题时也是可靠的。
图10为采用不同算法估算的油藏模型2渗透率场,可以看出,同样由于实测数据包含的信息不足以求解含有大量未知参数的反演问题,采用各算法估算的渗透率场与真实渗透率场差别都很大。
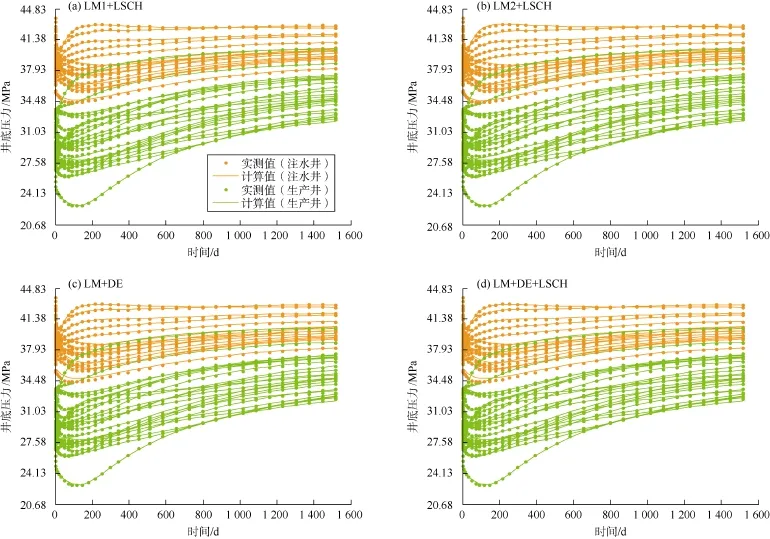
图8 油藏模型2基于不同算法得到的40口井的压力数据拟合结果
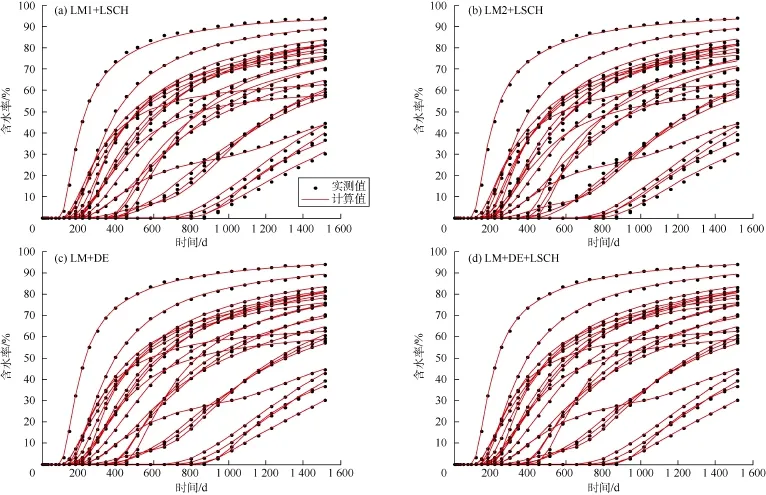
图9 油藏模型2基于不同算法得到的24口井的含水率数据拟合结果
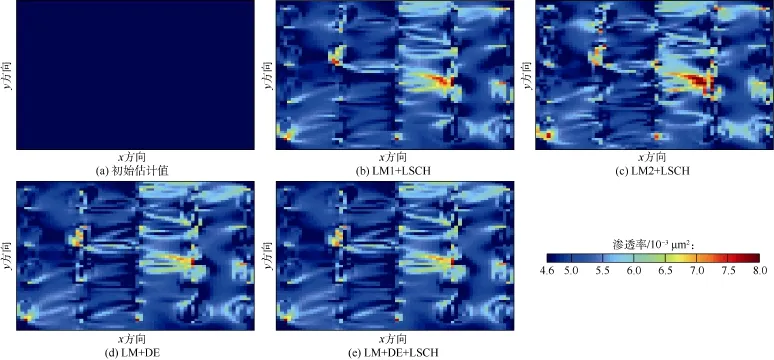
图10 油藏模型2基于不同算法估算的渗透率场
4 结论
本文采用DE算法替代试错法估算阻尼因子,改进了标准的Levenberg-Marquardt算法(称为LM+LSCH算法),提出了新的算法(称为LM+DE算法)。
新算法不需要进行线搜索,消除了使用试错法时存在的不确定性,解决了标准LM算法应用于大型反演问题可靠性较差的问题。
算例分析结果表明:LM+DE算法的收敛速度比LM+LSCH算法快;对于小型问题,当执行相同次数的LM迭代时,LM+DE算法的计算时间比LM+LSCH算法的计算时间长,但是对于大型问题LM+DE算法更省时;如果预设残差值作为LM迭代终止标准,使用LM+DE算法可以大幅减少迭代次数,从而节省总计算时间。
致谢:本研究得到了法赫德国王石油矿业大学(KFUPM)通过阿卜杜勒阿齐兹国王科技城(KACST)提供的计算设备支持,在此表示感谢。
符号注释:
c1,c2——系数;CR——交叉常数,CR∈[0,1];dcal,i——计算值矢量dcal的第i个元素;dmeas,i——实测值矢量的第i个元素;dobs——实测数据;dsim——模拟数据;F——目标函数;floor——向下取整函数;G——种群代次;g——目标函数的梯度;H——根据敏感度矩阵计算的Hessian矩阵:I——与H同等大小的单位矩阵;j——迭代步数;K——油藏渗透率矢量,10-3μm2;M——组成矢量τ的未知参数的个数;MF——突变因子,MF∈[0,2];N——数据点个数;Np——候选解初始种群大小;NSR——信噪比;randn——根据标准正态分布产生的随机数;rand——随机抽样函数;s——近似的牛顿方向;S——敏感度矩阵;α——模型参数矢量;β——比例因子;——试探向量;G+1η——突变向量;λ——LM算法中阻尼因子;——从第G代种群中所能找到的最优候选解;τk——由所有待估算的未知参数组成的矢量τ的第k个元素;τk,high,τk,low——矢量τ第k个元素的上限和下限;——从第G代种群中随机选择的几个不同的候选解,均有别于Gτ;υ——迭代步长。
[1]JACQUARD P,JAIN C. Permeability distribution from field pressure data[J]. SPE Journal,1965,5(4): 281-294.
[2]CHAVENT G,DUPUY M,LEMMONIER P. History matching by use of optimal theory[J]. Society of Petroleum Engineers Journal,1975,15(1): 74-86.
[3]YANG P H,WATSON A T. Automatic history matching with variable-metric methods[J]. SPE Reservoir Engineering,1988,3(3): 995-1001.
[4]SUN N Z,YEH W W. Coupled inverse problems in groundwater modeling: 1. Sensitivity analysis and parameter identification[J]. Water Resources Research,1990,26(10): 2507-2525. DOI: 10.1029/WR026i010p02507.
[5]MAKHLOUF E M,CHEN W H,WASSERMAN M L,et al. A general history matching algorithm for three-phase,three-dimensional petroleum reservoirs[J]. SPE Advanced Technology,1993,1(2): 83-92.
[6]ZHANG F,REYNOLDS A C,OLIVER D S. An initial guess for the Levenberg-Marquardt algorithm for conditioning a stochastic channel to pressure data[J]. Math. Geol.,2003,35(1): 67-88.
[7]NOCEDAL J S,WRIGHT S. Numerical optimization[M]. New York: Springer-Veriag,2006.
[8]O'LEARY D P. Scientific computing with case studies[M]. Philadelphia: SIAM Press,2009.
[9]ANTERION F,EYMARD R,KARCHER B. Use of parameter gradients for reservoir history matching[R]. SPE 18433-MS,1989.
[10]WOLFE P. Convergence conditions for ascent methods[J]. SIAM Review,1969,11(2): 226-235. DOI: 10.1137/1011036. JSTOR 2028111.
[11]HANSEN N,OSTERMEIER A. Completely derandomized self adaptation in evolution strategies[J]. Evolutionary Computation,2001,9(2): 159-195.
[12]AWOTUNDE A A. Estimation of well test parameters using global optimization techniques[J]. Journal of Petroleum Science & Engineering,2015,125: 269-277.
[13]LU P,HORNE R N. A multiresolution approach to reservoir parameter estimation using wavelet analysis[R]. SPE 62985-MS,2000. DOI: 10.2118/62985-MS.
[14]AWOTUNDE A A,HORNE R. An improved adjoint sensitivity computation for multiphase flow using wavelets[J]. SPE Journal,2012,17(2): 402-417.
[15]AWOTUNDE A A. A multi-resolution adjoint sensitivity analysis of time-lapse saturation maps[J]. Computational Geosciences,2014,18(5): 677-696.
(编辑 胡苇玮)
Improvement of Levenberg-Marquardt algorithm during history fitting for reservoir simulation
ZHANG Xian1,AWOTUNDE A A2
(1. Abu Dhabi Marine Operating Company,P. O. Box 303,Abu Dhabi,U. A. E; 2. King Fahd University of Petroleum & Minerals,Dhahran 31261,Kingdom of Saudi Arabia)
In order to estimate reservoir parameters more effectively by history fitting,DE (Differential Evolution) was proposed to estimate the optimum damping factor so that the standard Levenberg-Marquardt algorithm was improved,and the improved algorithm was validated by analysis of examples. The standard LM algorithm uses trial-and-error method to estimate the damping factor and is less reliable for large scale inverse problems. DE can solve this problem and eliminate the use of line search for an appropriate step length. The improved Levenberg-Marquardt algorithm was applied to match the histories of two synthetic reservoir models with different scales,and compared with other algorithms. The results show that: DE speeds up the convergence rate of the LM algorithm and reduces the residual errors,making the algorithm suitable for not only small and medium scale inverse problems,but also large scale inverse problems; if the iteration termination criteria of LM algorithm is preset,the improved algorithm will save the number of iterations and reduce the total time greatly needed for the LM algorithm,leading to higher efficiency of history matching.
numerical reservoir simulation; history matching; Levenberg-Marquardt algorithm; differential evolution; line search
TE319
A
1000-0747(2016)05-0806-10
10.11698/PED.2016.05.18
张鲜(1985-),男,四川南充人,硕士,阿布扎比海上运营公司研发部研究员,主要从事油藏描述及模拟等方面的研究工作。地址:Research & Development Division,Abu Dhabi Marine Operating Company,P. O. Box 303,Abu Dhabi,U. A. E。E-mail:XZhang@adma.ae
2015-07-20
2016-04-13

