多刚体系统的一致性控制研究

熊 涛

(南京邮电大学 自动化学院，江苏 南京 210023)



多刚体系统的一致性控制研究

熊 涛

(南京邮电大学 自动化学院，江苏 南京 210023)

基于非自治级联系统理论，以非完整移动机器人为研究对象，研究多刚体系统的一致性问题，提出了一种新的分布式控制器。通过引入持续激励扰动项，验证了无论参考信号是否为持续激励信号，所提出的控制器都能实现系统一致性的目的，且能一致到期望的参考值。利用李雅普诺夫方法对系统进行了稳定性分析。最后，对所提控制器进行数值仿真，结果验证了所提出的控制器的有效性。

非自治级联系统；多刚体系统；持续激励；非完整移动机器人

0 引言

多刚体系统的一致性控制在多机器人合作控制、交通车辆控制、无人机编队和网络资源分配等领域有着广泛的应用。多刚体系统姿态同步的控制方法主要包括：主从式控制法、基于行为的控制法以及虚拟结构控制法。文献[1]中，WANG P K和HADAEGH F Y提出了主从式(Leader-Follower)控制法，该控制方法将同步问题转化为一般的跟踪问题，优点是可以单独分析某个刚体的跟踪性能，而缺点是一旦Leader发生故障或失效，其他刚体将失去参考信号，无法完成同步目标，造成系统混乱。文献[1]作为该领域的开创性成果，研究了多领导者情况下的多刚体姿态协调控制，运用了近邻控制器的概念，使系统达到了全局渐近稳定。BALCH T和ARKIN R C提出了基于行为(Behaviour-based)的控制法[2]，根据相邻刚体的姿态变化来调整自身的变化，优点是某个刚体的故障或失效并不会影响到整个刚体群的运动，而只是影响相邻刚体的运动。文献[3]凭借局部信息交换，设计有效的控制律，解决了一队刚体的姿态对齐问题。 REN W和BEARD R W提出了虚拟结构(Virtual Structure)控制法[4]，假设刚体群中存在虚拟的单个刚体，每个刚体都根据该虚拟刚体调整自身的姿态。文献[4]中提出的集中式虚拟结构法使刚体群依赖于唯一的虚拟刚体，容易使其成为单个失效点，而文献[5-7]提出的分布式虚拟结构法则避免了该缺点。因此，后来的姿态同步问题多运用分布式控制法。本文针对平面二维多刚体系统，基于图论、非自治级联系统理论和非线性系统稳定性理论等方法，对多刚体系统的一致性控制问题进行探讨。

符号说明:令R表示实数集合，Rn表示n维实数列向量集合，Rm×n表示m×n实数矩阵集合，xT表示实数向量x的转置，diag{x1,x2,…,xN}表示对角元素为x1,x2,…,xN的对角矩阵，IN表示N阶单位矩阵，G表示图。

1 问题描述

本文以非完整移动机器人为研究对象，考虑由N个具有相同机械结构的非完整移动机器人组成的系统，运动方程由以下方程组表示：

(1)

其中，i=1,2,…,N。当i=d时，表示移动机器人组的期望参考轨迹，ud、ωd是已知的时变函数。根据相关图论知识，这N个移动机器人可以表示为图G=(V,E)的N个节点。通过输入和状态的转化，系统(1)可被转化为如下级联形式：

(2)

其中，xi1=θi，xi2=xi，xi3=yi，ui1=ωi，ui2=uicosθi。当i=d时，表示参考机器人方程的级联形式。

根据上述系统模型，控制目标可以概括为：对于每一个追随者，基于其本身及其邻居的状态，设计一个控制器，使系统中的机器人状态达到一致，且都一致于期望状态。但是在实际情况中，由于外部干扰、通信时延等因素的影响，要达到理想的一致是比较困难的，因此，实际的控制目标为：在合适的控制器和通信拓扑下，系统 (1) 中所有机器人的状态收敛到期望值的一个邻域内，即对系统(2)设计控制律使得：

(3)

(4)

其中，i，j=1,2,…,N，ε是一个大于0的常数，代表误差范围。

系统(1)写成矩阵形式为：

(5)

根据李代数相关秩的条件[8]，很容易证明系统 (5) 是可控的。然而，一个无漂移常规系统光滑稳定的必要条件是系统输入的数量等于状态的数量，因此，找不到静态光滑或连续的反馈控制器来稳定系统 (1) 。查阅文献[9]可知，运用线性时不变连续状态反馈可以实现系统的一致性。本节接下来将会研究已知期望参考轨迹的多刚体系统的一致性问题。

2 控制律设计

基于前述级联系统的形式及前期工作中已有的控制律：

(6)

其中，k0>0,k1>0是正常数，aij是系统通信拓扑结构图的邻接矩阵的元素，aij=1表示刚体i可以接收刚体j的状态信息，ai0=1表示刚体i可以接收参考刚体的状态信息；相反地，aij=0和ai0=0表示刚体i和刚体j以及参考刚体之间没有通信，无法得知它们的状态信息。

结合协调控制律ui2：

(7)

其中，k2>0，k3>0是正常数。

通过仿真研究可以看到，所有状态无法都达到一致，这说明基于积分器系统或线性系统的一致性结果不能直接沿用到非完整移动机器人系统中。基于此，本文针对两种不同期望的参考信号重新设计了控制律。

定义1[10]：存在正常数α1、α2和δ使以下不等式对所有t>0成立：

(8)

则称ud为持续激励。

(1)控制律ui1的设计

当ud1是持续激励信号时，显然，系统(1)的所有状态都是可控的。仍然采用控制器(6)来控制(1)的第一个子系统。

当ud1→0(或甚至ud1=0)时，首先定义刚体i与其邻居之间的平均距离为：

(9)

构造控制律ui1如下：

(10)

(2)控制律ui2的设计

首先，定义矩阵Z2=[x12,x22,…,xN2]T和Z3=[x13,x23,…,xN3]T。基于非完整移动机器人系统控制方面的研究结果，无论ui1收敛到持续激励信号或者是零，构造如下控制律：

ui2=-k2LZ2-k3ui1LZ3

(11)

其中，L∈Rn×n是系统无向连通图的Laplacian矩阵。

从公式(11)的结构可以看出，如果ud1→0(或甚至ud1=0)，那么所有xi1达到一致的速度快于Z2和Z3的一致速度，所以状态xi3将达不到一致。但由于控制律ui1设计时引入的持续激励扰动项ksin(t)，使系统保持可控，此时，运用所提出的控制律ui2可以使所有状态变量都达到一致。

3 稳定性分析

定理1 如果φ(t)是一个持久激励信号，k2>0和k3>0是常数，且L∈Rn×n是系统无向连通图的Laplacian矩阵，那么系统：

(12)

将达到指数一致。

证明：考虑无向图G的Laplacian势能相关函数作为Lyapunov函数：

(13)

当G是连通图时，上式为半正定，对其求导得：

(14)

可以看出，其导数为负半定。

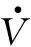
{[Z2,Z3]T|LZ2=0,LZ3=0}

(15)

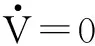
定理2(当ud1是持续激励信号时的一致性定理)假设系统通信拓扑结构是无向连通的，且至少有一个刚体能接收参考信号xd1的信息，则系统(1)在控制器(8)和(13)的控制下能达到一致。

证明：在控制器(6) 和(11)的控制下，闭环系统可以写成如下形式：

(16)

(17)

其中，Λui1=diag{u11,u21,…,uN1},Z1=diag{x11,x21,…,xN1},Λai0=diag{a10,a20,…,aN0}，Zd1=diag{xd1,xd1,…,xd1}。

将系统(16)中的ui1用ud1来替代，则系统(16)可视作系统：

(18)

被

(19)

级联，级联项为：

(20)

(1)如果系统的通信拓扑结构是连通的，且至少有一个刚体可以接收参考信号系统(2)的信息，则子系统将指数一致到ud1。

(2)根据定理1，当ud1是持续激励信号时，子系统(18)将达到指数一致。

(3)级联项(20)满足[Z2,Z3]T的线性增长条件。

那么，基于以上3个条件，并根据非自治级联系统的理论[10-12]，系统的通信拓扑结构是联通的，且至少有一个刚体可以接收参考信号时，系统中的N个刚体在控制器(6)和(11)的控制下能够达到期望的一致。

定理3(当ud1→0(或ud1=0)时的一致性定理)假设系统通信拓扑是无向连通的，且至少有一个刚体能接收xd1的信息，则系统(1)在控制器(10)和(11)的控制下达到一致。

证明:

(1)当ρi≥ε时

这种情况下，在控制器ui1的设计中引入持久激励信号来保证整个系统的可控性，例如控制器(10)中的ksin(t)。对于子系统(19)，在连通通信拓扑结构下，ui1将收敛到ksin(t)。对于子系统，在控制器(10)的控制下，根据非自治系统的级联理论，以及φ(t)=ksin(t)时定理1的指数一致结果，可得出ρi<ε。

(2)当ρi<ε时

在这种情况下，系统的通信拓扑结构是连通的，且至少有一个刚体能接收参考信号，当ρi在ε领域内自由取值时，系统(19)能收敛到原始的参考信号。那么，在控制器(10)和(11)控制下，多刚体系统的实际一致性问题得到解决。

基于定理2和定理3，通过证明可知，在重新设计的控制器中，无论ud1是否是持续激励信号，多刚体系统都能达到一致性。

4 仿真结果

本节将所提出的控制器与前期工作所设计的控制器进行比较。在现有的控制律(6)和(7)下，基于无向连通拓扑结构，k0=1,k1=1,k2=5,k3=6。从图1中可以看到，无法让第三个状态达到一致。

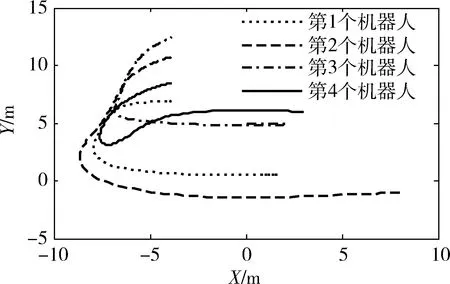
图1 每个刚体的运动轨迹

由于参考信号趋于零的情况下非完整移动机器人系统的一致性研究较少，为了阐述本文所提出的控制器的有效性，以下将进行两种不同参考信号的仿真。

(1)ud1=0

选取系数：k0=1,k1=1,k2=5,k3=6，误差范围为：ε=0.000 01。系统初始状态为：

基于定理3中提出的一致性协议，仿真结果显示如图2～图5，从图中可以看到，每个机器人状态都能达到一致。

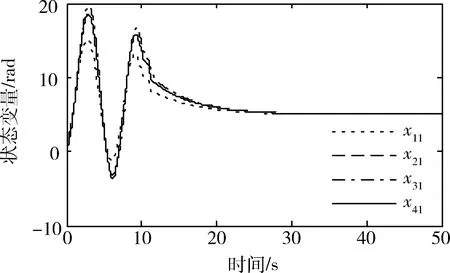
图2 ud1=0时第1个状态的一致性

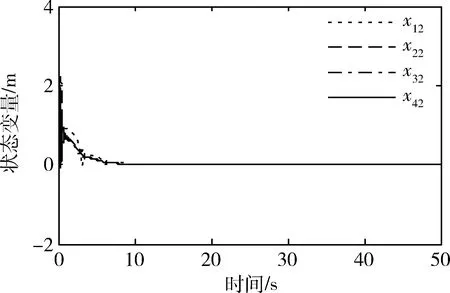
图3 ud1=0时第2个状态的一致性

图4 ud1=0时第3个状态的一致性

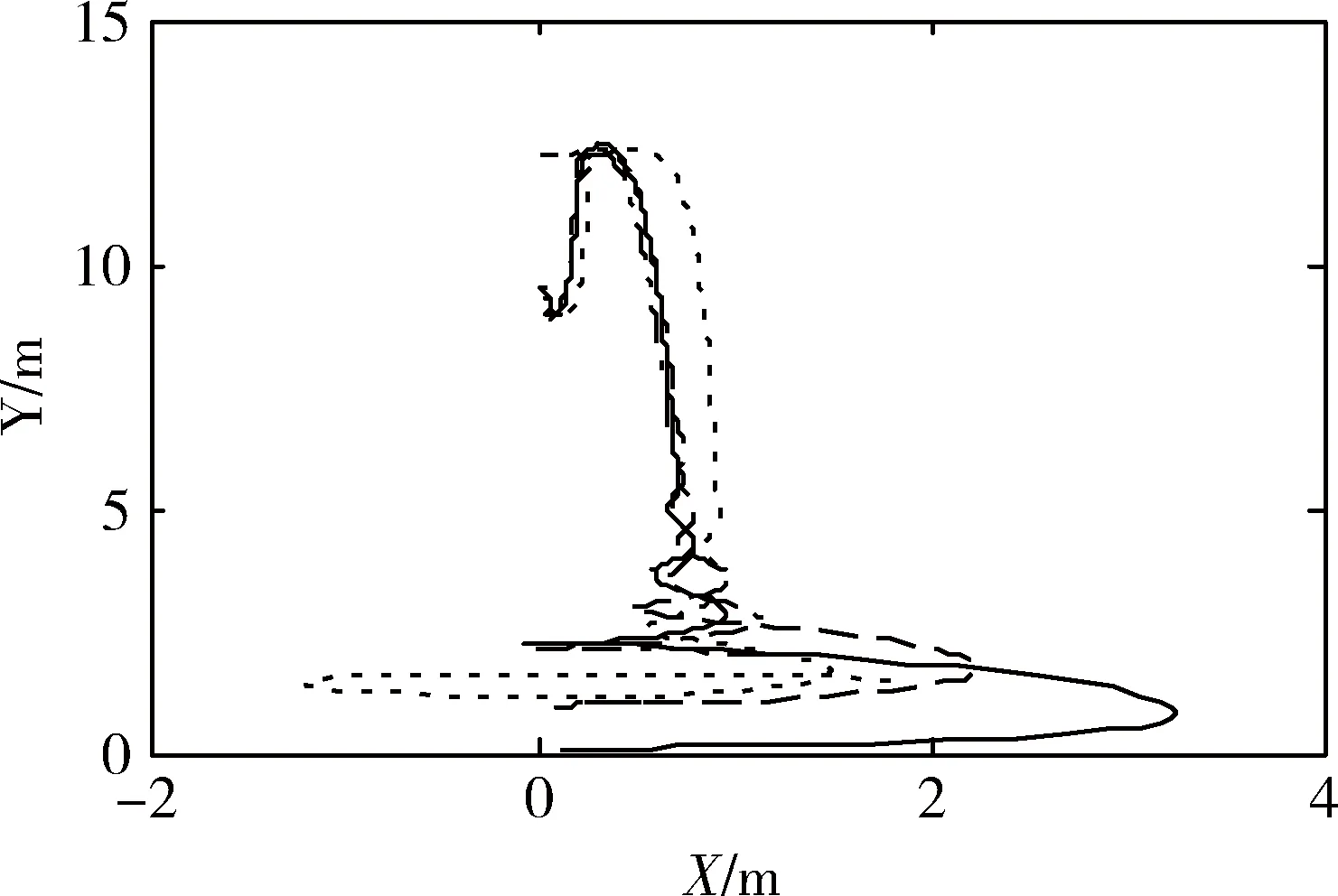
图5 ud1=0时每个刚体的运动轨迹

(2)ud1=3sin (0.2t)

这种情况下，参考信号为一个持久曲线信号，取k0=8,k1=1,k2=5,k3=6，系统初始状态为：

仿真结果如图6～图9，基于定理2中的一致性协议，仿真结果表明每个刚体都能达到一致，从运动轨迹图中可以看到，所有的刚体最后都收敛到一起，并呈一定的曲线运动，从仿真图中可以看出本文所提控制器能有效实现系统一致性。

图6 ud1=3sin (0.2t)时第1个状态的一致性

图7 ud1=3sin (0.2t)时第2个状态的一致性

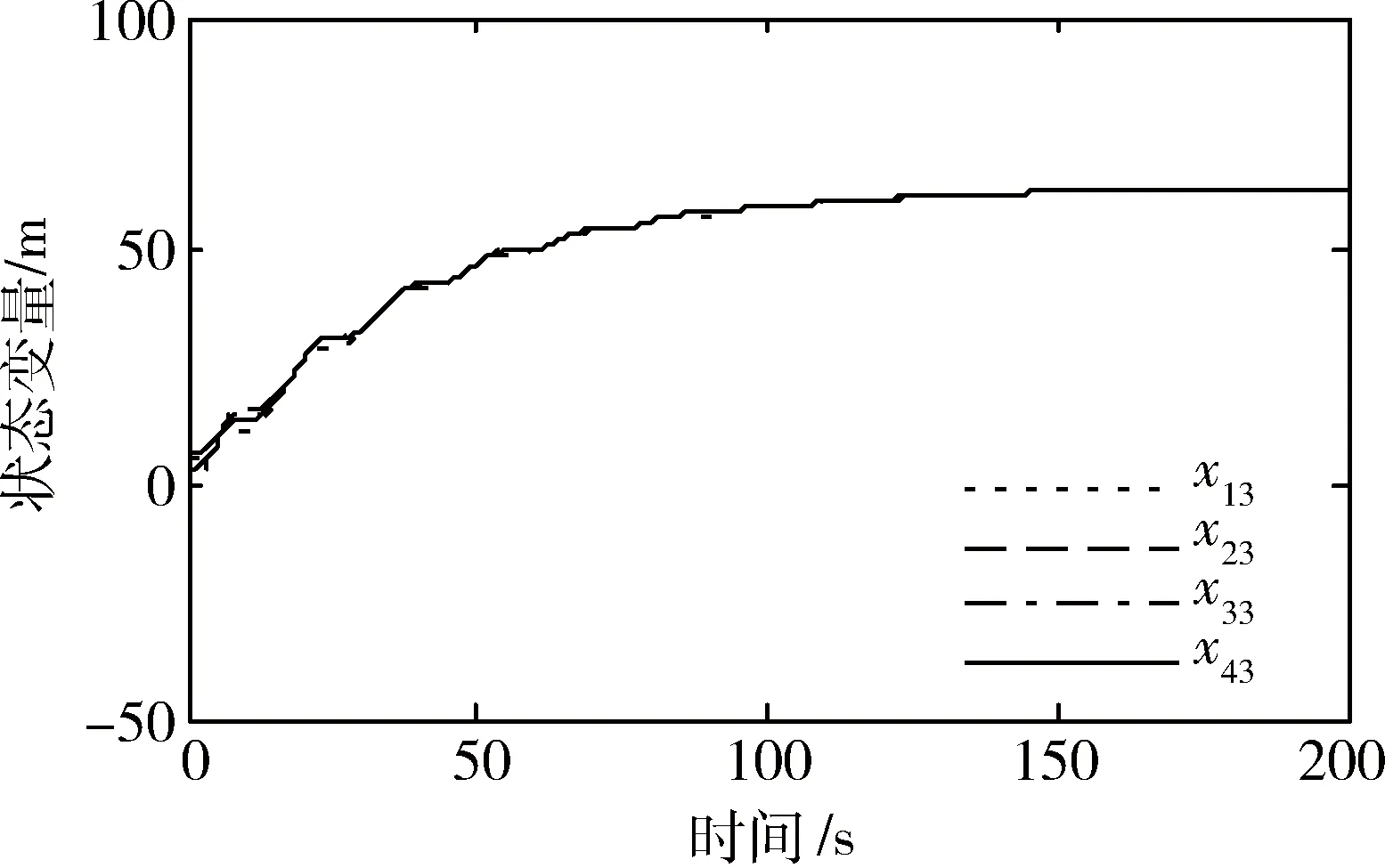
图8 ud1=3sin (0.2t)第3个状态的一致性

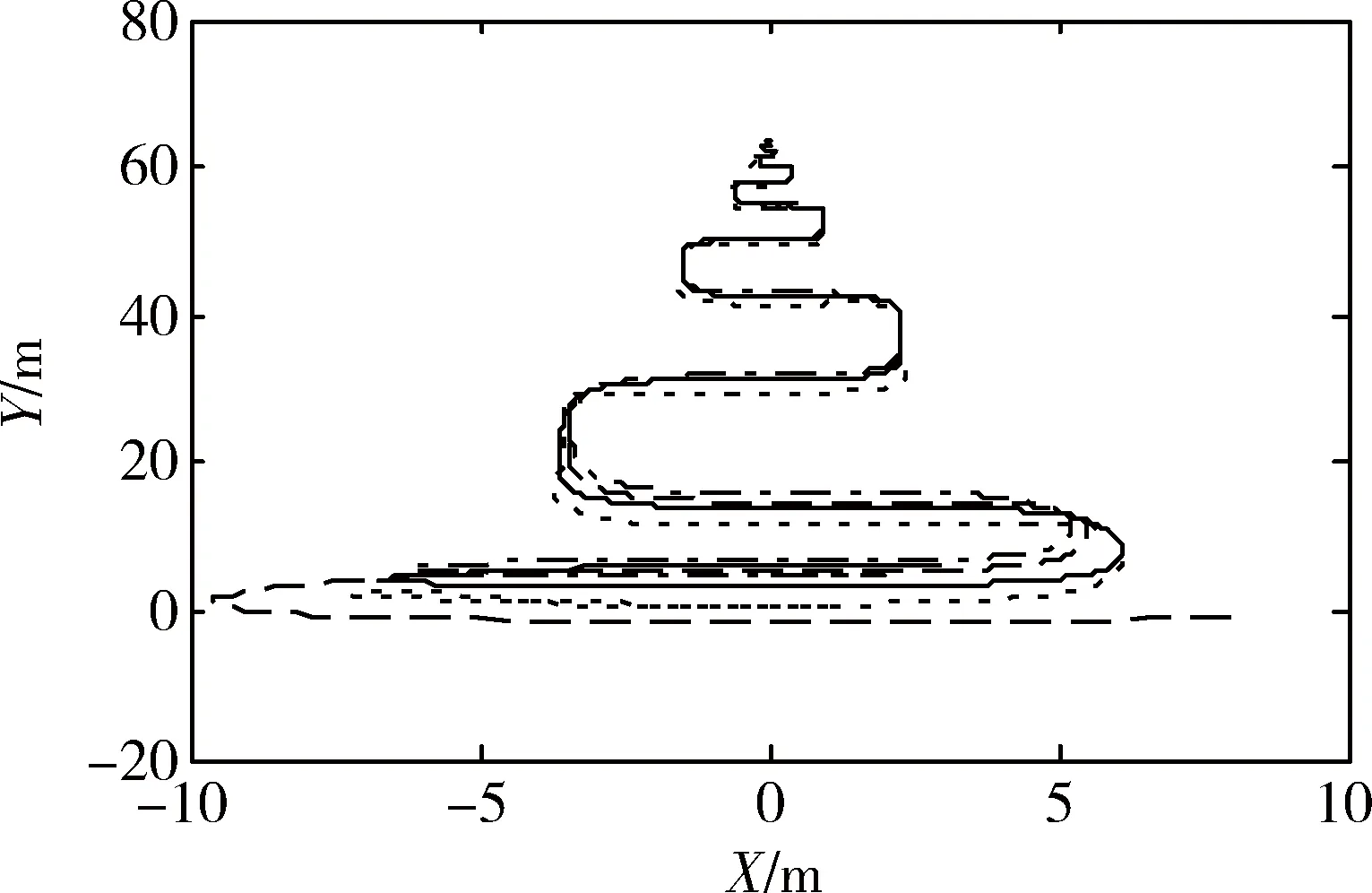
图9 ud1=3sin (0.2t)时每个刚体的运动轨迹

5 结论

本文利用非自治级联系统理论，提出了一种具备无论系统参考信号是否为持续激励信号都能实现系统一致性的分布式控制器。该控制器的设计通过在控制律中引入持续激励扰动项，改善了前期工作的缺点，在参考信号不为持续激励信号时，也能让系统达到一致性。最后，将所提控制方法应用到两种不同参考信号的情况中，仿真结果验证了所提出的控制方法的有效性。

[1] WANG P K C,HADAEGH F Y.Coordination and control of multiple microspacecraft moving in formation [J].Journal of the Astronautical Sciences,1996,44(3): 315-355.

[2] BALCH T,ARKIN R C.Behavior-based formation control for multirobot teams [J].IEEE Transactions on Robotics and Automation,1998,14(6): 926-939.

[3] Ren Wei.Distributed attitude alignment in spacecraft formation flying [J].International Journal of Adaptive Control and Signal Processing,2007,21(2-3): 95-113.

[4] Ren Wei,BEARD R W.Virtual structure based spacecraft formation control with formation feedback [C].AIAA Guidance,Navigation,and Control Conference and Exhibit.2002: 2002-4963.

[5] Ren Wei,BEARD R W.Decentralized scheme for spacecraft formation flying via the virtual structure approach [J].Journal of Guidance,Control,and Dynamics,2004,27(1): 73-82.

[6] Zou Anmin,KUMAR K D,Hou Zengguang.Attitude coordination control for a group of spacecraft without velocity measurements [J].IEEE Transactions on Control Systems Technology,2012,20(5): 1160-1174.

[7] ABDESSAMEUD A,TAYEBI A,POLUSHIN I G.Attitude synchronization of multiple rigid bodies with communication delays [J].IEEE Transactions on Automatic Control,2012,57(9): 2405-2411.

[8] ISIDORI A.Nonlinear control systems [M].Springer Science & Business Media,1995.

[9] Dong Wenjie,FARRELL J A.Cooperative control of multiple nonholonomic mobile agents [J].IEEE Transactions on Automatic Control,2008,53(6): 1434-1448.[10] Zhou Jiakang,Ma Guangfu,Hu Qinglei,et al.Delay depending decentralized adaptive attitude synchronization tracking control of spacecraft formation[J].Chinese Journal of Aeronautics,2012,25(3): 406-415.

[11] PANTELEY E,LORIA A.On global uniform asymptotic stability of nonlinear time-varying systems in cascade [J].Systems & Control Letters,1998,33(2): 131-138.

[12] 齐玉峰.非线性级联系统的稳定性分析及控制设计[D].天津:天津工业大学,2006.

Research on consistency control of multiple rigid systems

Xiong Tao

(College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

This paper proposes a new distributed controller to control nonholonomic mobile robot,which as a special object of multi-rigid-body system,by utilizing the nonautonomous cascade system basic theory.By introducing a persistent excitation disturbance term,it is verified that the proposed controller can achieve system consistency and even can converge to expected reference value for all robots,whatever the

ignal is persistent excitation disturbance.A stability analysis is presented using Lyapunov’s direct method.Finally,simulation results illustrate the efficiency of proposed controller compared with the previous works.

nonautonomous cascade system; multiple rigid systems; persistent excitation; nonholonomic mobile robot

TP273

A DOI：10.19358/j.issn.1674-7720.2016.19.025

熊涛.多刚体系统的一致性控制研究[J].微型机与应用，2016,35(19)：84-88,94.

2016-06-15)

熊涛(1991-)，男，硕士研究生，主要研究方向：非线性系统，协调控制，鲁棒控制。