基于误差修正时间序列模型的短期电力需求预测分析

王飞燕

（兰州财经大学，甘肃 兰州 730000）

基于误差修正时间序列模型的短期电力需求预测分析

王飞燕

（兰州财经大学，甘肃 兰州 730000）

随着经济、社会和工业的快速发展，电力需求突飞猛进.电力行业也逐渐成为影响全球社会经济发展地位的重要的因素，不准确的需求预测增加了电力行业的运行成本，特别是在市场环境中，精度即意味着金钱，准确的电力需求预测是有价值的。本文主要对许昌市短期电力需求进行分析预测，利用许昌市用电量的相关数据，分别应用移动平均法、时间序列法建立模型并对模型进行预测和分析，再通过对这两种预测方法分别赋予不同的权重建立加权组合预测模型来改进预测误差，通过比较分析得出加权组合模型预测的精度更高。

移动平均法；电力需求预测；时间序列法；加权组合预测法

随着经济的快速发展，世界各国对能源的需求量也日益增加，再加上电力资源清洁、经济适用以及比较方便等优点，因此，各国都在致力于不断提高本国的电气化程度，从而来改善人民的生活并促进经济的发展。与此同时，党的十八大也对新一时期电力能源的发展做出了总部署，并提出“控制能源消费总量，加强节能降耗，支持节能低碳产业和新能源、可再生能源发展，确保国家能源安全”等要求。当前，我国为加强区域电力建设引入电力市场管理模式，通过对区域电力需求做出科学的分析和预测，以此来保证区域经济稳定并且健康地发展。

1　背景介绍

电力需求的短期预测是组成电力系统发电计划的重要部分，电力需求预测的结果是电力系统正常运行工作的基础数据，其预测的精度可直接影响电力系统运行的经济性及安全性，所以任何时候的首要任务均是要准确地预测电力需求量，因此，电力需求预测，尤其是短期、超短期预测是电力系统安全和经济稳定发展的前提与保障。电力需求的短期预测同时也是电力公司制定生产计划并进行发展规划的重要依据，且准确的电力需求预测在保证用电需求以及增强供电可靠性的基础上能够有效地降低发电成本，故不准确的需求预测增加了电力行业的运行成本，特别是在市场环境中，精度即意味着金钱。与此同时，电力需求增加的有效的预警对于确保供给和需求之间的平衡也是非常重要的。因此，电力系统可以通过开发一个对电力需求的跳读算法实现优化。

另外研究电力需求的其他原因，首先便是二氧化碳的排放，煤和燃煤电力是典型的向上流和向下流行业，由煤炭消耗产生的热能和巨大的环境压力不容忽视，因为发电的高比例，中国排放的热能约占总二氧化碳排放量的。因此，准确和及时的电力需求预测可以为合理发电计划与调整电力政策和结构提供可靠的依据，并大大减少二氧化碳排放量。其次，输电网格安全影响国家安全，网格在许多国家经常发生故障，造成大面积的停电，这严重影响了人民的生活并造成了巨大的经济损失。

2　模型理论

2.1移动平均法

2.1.1基本思想

对于一个时间序列 ｛x2｝，假定在一个比较短的时间间隔里，序列的取值比较稳定，故可以用一段时间间隔内的平均值作为某一期的预测值。在实践中，m期移动平均法是较为常用的预测方法。假设最后一期的观察值为xi，那么利用m期移动平均法向前预测第l期的值为：

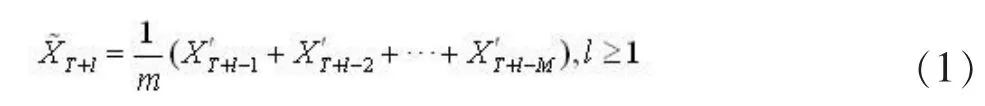
2.1.2实例分析

根据许昌市统计局2014年各月统计月报数据，利用2012.1-2014.12的社会用电量的月度数据，通过选择不同的移动平均间隔长度m，对于许昌市社会用电量的月度数据进行计算各自的均方误差，利用Excel软件计算各自的均方误差，当m=3时，SSE=0.9886，当m=4时，SSE=0.9906；当m=6时，SSE=1.2370；当m=12时，SSE=1.4822。由此可知，当取间隔长度为3时，预测值与实际观测值之间的相对误差较小，基本都［-10%，10%］范围内浮动，此时，利用该模型进行短期预测得到的预测精度较高。

2.2时间序列法

2.2.1模型

许多非平稳序列差分后会显示平稳序列的性质，这时称这个非平稳序列为差分平稳序列，并对该差分平稳序列可以使用ARINA模型进行拟合.具有如下结构的模型称为求和自回归移动平均模型，简记为ARZNACP，d，q模型：

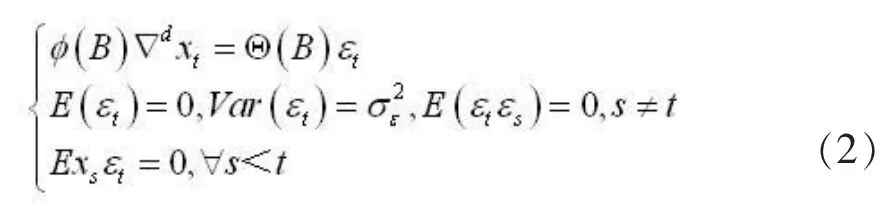
2.2.2实例分析

取许昌市社会用电量（2012.1-2014.12）的月度时间序列X作为研究对象，首先利用Eviews软件对其分析，许昌市社会用电量及其残差序列均呈现线性上升趋势，而一阶差分序列值在［-1，1］范围内围绕零上下作随机波动，由此可知，原观察值一阶差分后平稳.再根据原序列的自相关函数与偏自相关函数图，可以明显看出自相关函数和偏自相关函数均2阶截尾，故可对该时间序列使用ARIMA（2，1，2）进行拟合.AR（1）、AR（2）的系数均不存在显著性，因此需要将其剔除后再进行估计。

最终检验结果显示，AR（1）、AR（2）的系数均通过了显著性检验，故对应的模型为ARIMA（0，1，2），其表达式为：DXt=0.1087+εt-0.3284εt-1.-0.6674εt-2其中，输出结果中0.1087是DXt的均值，表示月平均用电量增量是0.1087亿kw·h。

移动平均法、时间序列法的单一模型预测值分别为：2015年1月 （7.50、8.31），2015年2月（7.73、8.41），2015年3月 （7.73、8.51），2015年4月（7.55、8.62），2015年5月（7.63、8.73）。

3　加权组合预测模型

加权组合预测理论认为，对同一个预测问题使用多个不同预测模型的线性组合，在一定条件下可以有效地改善模型的拟合能力和提高预测精度。利用加权组合预测模型进行电力需求预测可以将各个模型有机地组合在一起，综合各个模型的优点，提供更准确的预测结果。

3.1权重的确定

组合预测法的关键在于如何确定组合权重系数，对权重的选择应使误差越小越好。当单个单一预测模型的预测精度完全已知时，一般采用加权平均的方法。简单加权平均法先把各个单一预测模型的预测误差的方差和进行排序，根据各个单项预测模型的误差方差和的加权系数成反比可知，排序越在前的单一预测模型，其在组合预测中的加权系数就应越小即：

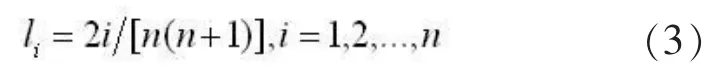
3.2实例分析

3.3模型评价

为了进一步检验各模型预测结果的好坏，可以对模型进行进一步的评价：

式中yi为变量观察值，为变量预测值，m为样本量.根据上述各评价指标进行预测，得到结果为：移动平均法 （SSE=32.6233，MAE=0.801，MSE=0.1731，MAPE，0.1236），时间序列法（SSE=27.4915，MAE=0.6786，MSE=0.1498，MAPE= 0.1145），简单加权平均法（SSE=22.2554，MAE= 0.6426，MSE=0.1430，MAPE=0.1016）。

由此可知，加权组合预测法的结果明显优于单一预测方法，从而说明加权组合预测法的有效性。所以，可以采用简单加权平均法组合预测模型来对未来几个月的用电量进行预测，结果为2015年1月为 8.09，2015年 2月为 8.23，2015年 3月为8.29，2015年4月为8.30，2015年5月为8.38。

［1］ 朱琳.电力系统负荷预测方法及其应用［D］.华北电力大学MBA学位论文，2011：1-2.

［2］ Yuanyuan Wang，Jianzhou Wang，Ge Zhao，Yao Dong.Appli cation of residual modification approach in seasonal ARIMA for electricity demand forecasting：A case study of China［J］. Energy Policy48（2012）：284-285.

［3］ 陈旭东，查艳婷.基于GM（1，1）模型对浙江人口的预测［J］.科教导刊.2012（8）：217.

［4］ 黄向阳，金阳等.精算中常用的统计模型［M］.北京：中国人民大学出版社，2009.

［5］ 高铁梅.计量经济分析方法与建模：EViews应用及实例（第2版）［M］.北京：清华大学出版社，2009（5）：157.

［6］ 徐国祥.统计预测和决策（第3版）［M］.上海：上海财经大学出版社，2008（11）.

［7］ 戴华娟.组合预测模型及其应用研究［D］.中南大学硕士学位论文，2007（5）：25-26.

［8］ 卓东.组合预测模型研究及其在电力负荷预测中的应用［D］.兰州商学院硕士学位论文，2007（5）：55-56.

C812